格上基于身份的群签名方案

汤永利 李元鸿 张晓航 叶 青

1(河南理工大学计算机科学与技术学院 河南焦作 454003)2(河南工业和信息化职业学院 河南焦作 454003)(yltang@hpu.edu.cn)

群签名由Chaum等人[1]在1991年提出，是密码学领域中的一个重要概念.在群签名中，合法群成员能够代表整个群进行签名，但是无法通过签名来确定签名者的身份信息，即群签名有匿名性.此外，当有争议发生时，群管理员能够利用追踪密钥打开签名并得到签名者的真实信息，即群签名有可追溯性.匿名性和可追溯性使得群签名能够在多种场景下得到应用，例如，匿名电子投票、受信计算平台以及电子商务系统等.

近几年，量子计算机的研究不断取得突破，一旦量子计算机得到应用，基于传统数论难题构造的群签名就能够在概率多项式时间(probabilistic poly-nomial time, PPT)内被攻破，因此建立在最坏情况困难性假设上的格密码成为了后量子密码时代的研究热点.2010年，Gordon等人[2]在随机预言模型下提出了第1个格上的群签名方案，并且将该方案的匿名性和可追溯性分别规约到容错学习(learning with errors, LWE)问题和GapSVP(gap shortest vector problem)问题，但其密钥和签名的开销过大.随后，Laguillaumie等人[3]提出了一种更为高效的格上群签名方案，将其方案的可追溯性规约至小整数解(short integer solution, SIS)问题上，同时优化了密钥长度和签名长度，但代价是公共参数开销较大.2015年，Nguyen等人[4]和Ling等人[5]设计了2种不同的格上群签名方案，前者使用了与身份编码技术相结合的非交互零知识证明协议，使得该方案的结构更为简单，而后者基于多项式环以及环上小整数解(ring short integer solution, RSIS)、环上容错学习(ring learning with errors, RLWE)问题，具有更低的存储开销和时间复杂度.张彦华等人[6]利用文献[4]提出的身份编码技术构造了支持验证者本地撤销的群签名.Libert等人[7]基于Merkle Hash树以及Stern非交互式零知识证明协议，提出了第1个不依赖GPV陷门[8]的格上群签名方案.2017年，Ling等人[9]提出了完全动态的群签名方案，允许用户动态地加入和离开群组，李雪莲等人[10]在此基础上构造了新的群成员撤销机制，支持动态地加入和撤销用户.2018年，Ling等人[11]提出了固定签名长度的群签名方案，该方案利用Ducas等人[12]提出的签名算法设计了零知识证明协议，使密钥大小和签名大小都与用户成员数N无关.Pino等人[13]基于小型的零知识证明[14]构造了计算效率更高和存储开销更小的群签名方案.2019年，Katsumata等人[15]提出了标准模型下的格上群签名，该方案没有使用零知识证明系统，提高了运算效率，且满足CCA(chosen ciphertext attack)自身匿名性和完全可追溯性.2020年，Sun等人[16]和Canard等人[17]在文献[15]的基础上进行了改进.但上述的格上群签名方案均基于传统公钥基础设施(public key infrastructure, PKI)进行构造，无法抵抗公钥伪造攻击，且存在PKI体系中复杂的用户证书管理问题.

基于身份的加密体制(identity based encryption, IBE)是另一种密码学原语，由Shamir[18]于1984年提出.在基于身份的密码体制中，密钥生成中心(key generation center, KGC)根据用户的身份信息，例如：姓名、身份证号、电子邮箱等生成用户公钥，并使用用户身份信息和系统私钥计算生成对应的私钥并发放给用户，有效地避免了PKI体系中公钥证书管理的问题.Ibraimi等人[19]、Emura等人[20]分别提出了基于身份的群签名方案，但都基于有限域离散对数的传统数论难题，难以抵抗量子算法的攻击.

本文将格上的群签名与基于身份加密体制相结合，提出了一种格上基于身份的群签名方案.主要贡献有2个方面：

1) 通过环上陷门生成算法[5]生成系统公钥和系统主密钥，再利用格基委派技术[21]和原像采样算法生成用户私钥，采用拒绝采样算法[22]和经过Naor-Yung变换[23]的双重加密算法[24](LPR加密算法)生成签名.在Bellare等人[25]的群签名安全模型下，对所提方案进行严谨的安全证明.证明结果表明，在随机预言模型下，所提方案满足正确性、完全匿名性、不可伪造性以及完全可追溯性.其中，完全匿名性可规约至RLWE困难性假设，不可伪造性和完全可追溯性可规约至RSIS困难性假设.

2) 将本文方案与4个现有的格上群签名方案[7,9,11,26]进行了效率比较，分析比较结果表明，与其他方案相比，本文方案具有更小的密钥和签名尺寸.且由于使用了拒绝采样技术，本文方案在签名时避免零知识证明系统的并行重复，有效地提高了签名和验证过程的计算效率.

1 预备知识

1.1 符号说明

表1对本文出现的符号进行简要的说明.

Table 1 Symbol Description表1 符号说明

1.2 格的相关定义

定义1.系数映射和环同态映射.给定多项式v=v0+v1x+…+vn-1xn-1∈Rq，令τ(v)=(v0,v1,…,vn-1)T∈令Rot(v)=(τ(v),τ(v·x),…,τ(v·xn-1))∈对于Rot(A)=(Rot(a1),Rot(a2),…,Rot(am))∈

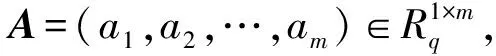
定义3.DRLWEn,m,q,χ问题[24].给定n,m≥1，q≥2，R上的一个概率分布χ.对于s∈Rq，随机选取a←Rq和e←χ，定义由(a,b=a·s+e)产生的分布为As,χ.DRLWEn,m,q,χ问题是指判别m个样本是取自分布As,χ还是取自分布U(Rq×Rq).

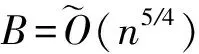
1.3 离散高斯分布和拒绝采样算法

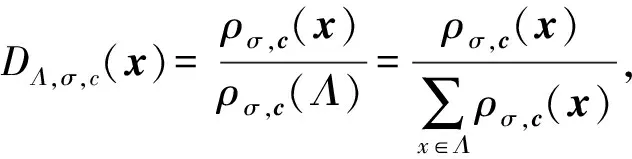
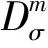
引理1[13].给定σ>0，正整数m，和任意正整数k>0，则式1)～2)成立：

引理2.拒绝采样算法[22].令V={v∈为1个概率分布，则存在常数M=O(1),使得2个算法①～②的输出在统计上的距离小于2-ω log m/M：

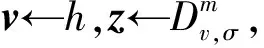
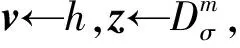
1.4 相关算法

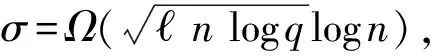
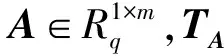
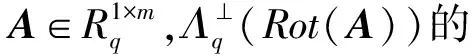
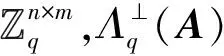
2 基于身份的群签名定义及安全模型

定义5.基于身份的群签名.结合Bellare等人[25]和Shamir[18]的定义，1个基于身份的群签名方案有5个多项式时间算法：

1)Keygen(1n,1N).输入安全参数n和群成员的最大可能个数N，输出系统公钥PK，管理员追溯密钥gtk以及系统主密钥gmk.

2)Extract(PK,gmk,IDπ).输入系统公钥PK，系统主密钥gmk以及用户π的身份信息IDπ，输出用户私钥gskπ=(xπ,1,xπ,2).

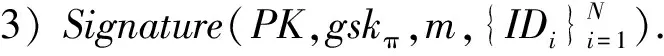
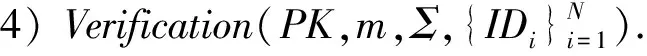
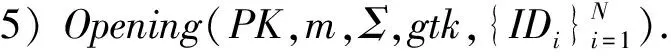
基于身份的群签名需要满足正确性、匿名性、不可伪造性和完全可追溯性.其中，群签名的正确性包括验证正确性和打开正确性；匿名性是指攻击者无法确定一个群签名具体是由群中哪个用户生成的，而本文方案具有的完全匿名性又称作CCA匿名性[4,15]，是指在允许攻击者A进行签名问询和打开问询后仍然能够保持签名的匿名性，具体见定义6；不可伪造性是指在没有群成员签名密钥的情况下，攻击者无法生成有效的群签名，具体见定义7；完全可追溯性是指任意1个合法的群签名一定能够被群管理员通过追踪密钥打开，具体见定义8.本文通过攻击者A和挑战者C之间进行的一系列游戏来刻画基于身份群签名的安全性定义.在随机预言模型下，攻击者A能够访问随机预言机并且向挑战者C进行3种问询：

1) 签名问询.攻击者A选择群中成员j∈[N]以及待签消息m∈{0,1}*进行问询，C运行Signature()签名算法使用IDj对应的私钥gskj对m进行签名，并返回对应的Σ给A.

2) 私钥问询.A选择群中成员j∈[N]进行问询，C运行Extract()私钥提取算法返回IDj对应的私钥gskj.

3) 打开问询.A选择消息m∈{0,1}*及其对应的群签名Σ进行问询，C运行Opening()打开算法，如果Σ由群中用户j∈[N]合法产生，则返回用户j的身份信息IDj，否则返回⊥.

定义6.完全匿名性[4,15].与CPA匿名性不同，完全匿名性(CCA匿名性)是指挑战者C在问询阶段授予攻击者A签名问询和打开问询的权限，攻击者A赢得4个阶段的游戏的优势仍然是忽略的:

1) 系统建立.挑战者C输入安全参数λ和用户数N诚实地运行Keygen(1n,1N)算法，得到系统公钥PK管理员追溯密钥gtk以及系统主密钥gmk，将系统公钥PK和群用户私钥gskj发送给攻击者A.

2) 问询阶段.攻击者A可以访问预言机并进行系统建立阶段的签名问询和打开问询.

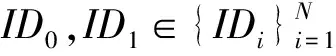
4) 猜测阶段.攻击者A对签名者身份进行猜测，得出b*∈{0,1}，若满足条件b*=b，则称A赢得了完全匿名性游戏.

定义A赢得游戏的优势为

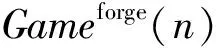
1) 系统建立.输入安全参数λ和用户数N，挑战者C诚实地运行Keygen(1n,1N)算法，得到系统公钥PK，管理员追溯密钥gtk以及系统主密钥gmk，将系统公钥PK和追溯密钥gtk发送给攻击者A.

2) 问询阶段.攻击者A被允许进行上述的签名问询和私钥问询.

3) 伪造阶段.攻击者A给出关于消息m*的签名Σ*，判断是否满足条件(①～③)：

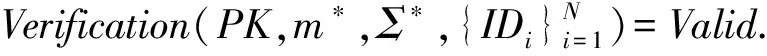
② A未对群成员j∈[N]进行过私钥问询.

③ A未对消息m*以及群成员j∈[N]进行过签名问询.

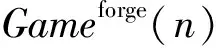
定义攻击者A赢得不可伪造性游戏的优势为

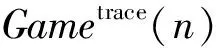
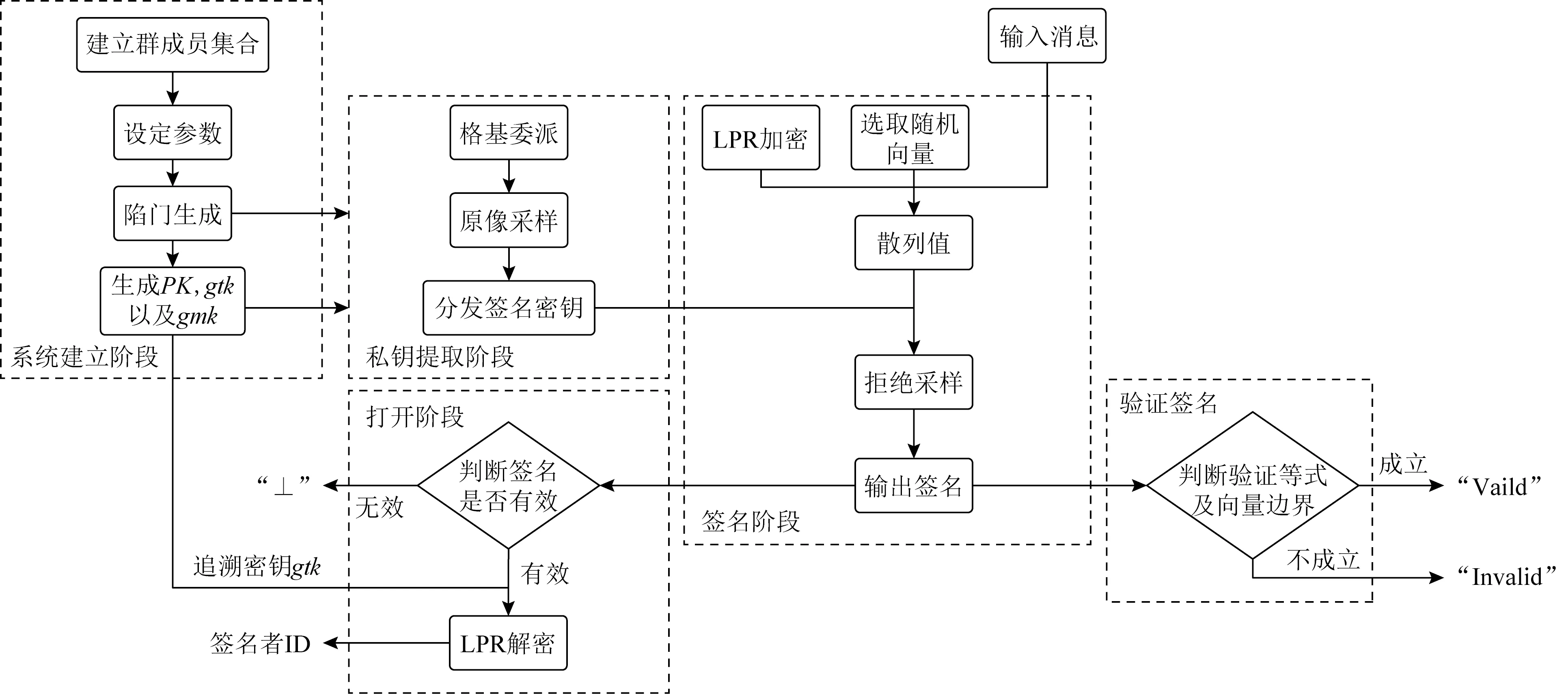
Fig. 1 The flow chart of identity-based group signature on lattice图1 格上基于身份的群签名方案流程图

1) 系统建立.挑战者C输入安全参数λ和用户数N诚实地运行Keygen(1n,1N)算法，得到系统公钥PK管理员追溯密钥gtk以及系统主密钥gmk，将系统公钥PK和追溯密钥gtk发送给攻击者A.

2) 问询阶段.攻击者A能够访问预言机并进行上述的签名问询和私钥问询.令Γ用来存储经过私钥问询的j；令Ι用来存储经过签名问询的(j,m).

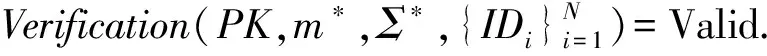
定义A赢得完全可追溯游戏的优势为

3 方案构造

本文结合引理3～5的算法构造了一个随机预言模型下的格上基于身份的群签名方案，核心思想是使用引理3的陷门生成算法建立，并获得系统公钥和主密钥，然后利用引理5的格基委派技术和引理4的原像采样算法提取用户身份信息并生成用户公私钥.在签名生成阶段使用引理2的拒绝采样技术以一定概率生成签名，并使得签名的概率分布与签名私钥的分布相独立，签名过程中同时使用了LPR双重加密算法，能够将本文方案的完全匿名性规约到RLWE困难假设下.方案的流程图如图1所示.

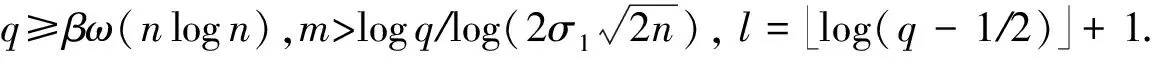
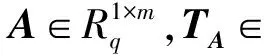
④ 输出系统公钥PK=(A,B,u,a,b)，追溯密钥gtk=s，主密钥gmk=TA.

2) 私钥提取Extract(PK,gmk,IDπ).此步骤由KGC运行.输入系统系统公钥PK，系统主密钥gmk以及用户身份IDπ，KGC进行如下操作提取用户私钥：

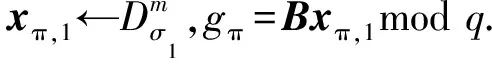
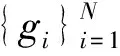
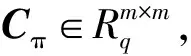
④ 计算xπ,2←SamplePreRq(Dπ,Tπ,u-gπ,σ1).

⑤ 输出用户私钥gskπ=(xπ,1,xπ,2).

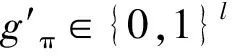
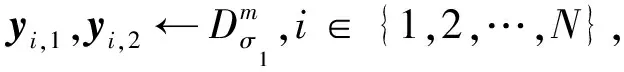
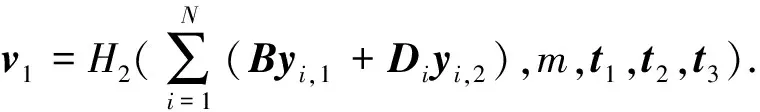
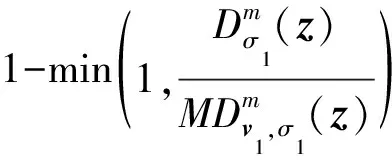
⑤ 输出用户π对m的群签名Σ=((zi,1,zi,2)1≤i≤N,v1,t1,t2,t3).

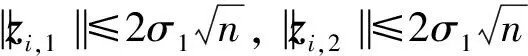
③ 如果步骤①和②都成立，则验证者返回“Valid”，即认为群签名Σ为群中某一成员对消息m的有效签名；否则验证者返回“Invalid”.

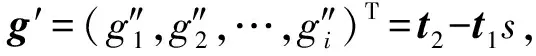
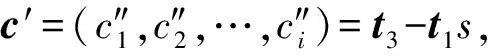
③ 根据每个用户的身份信息IDi计算出对应的Di，验证gk是否满足等式

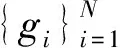
④ 如果步骤③成立，则证明打开成功，并且返回用户身份IDk；否则打开失败，返回“⊥”.

4 安全性证明

此部分对所提方案的正确性、完全匿名性以及完全可追溯性3个重要的安全属性进行详细的证明，并且将完全匿名性和完全可追溯性分别规约到RLWE和RSIS问题上.

定理1.正确性.本文提出的方案是正确的，即一个真实的签名是能够被成功验证和打开的.

证明.

1) 验证正确性.

假设Σ=((zi,1,zi,2)1≤i≤N,v1,t1,t2,t3)是群中用户π对消息m按照签名算法产生的签名，则下列等式成立：

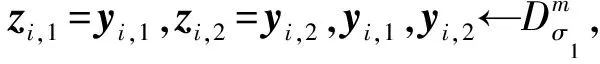
本方案的验证正确性得以满足.

2) 打开正确性.

假设Σ=((zi,1,zi,2)1≤i≤N,v1,t1,t2,t3)是群中用户π对消息m的有效签名.

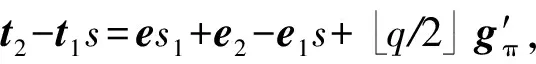
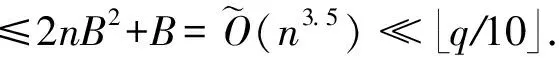
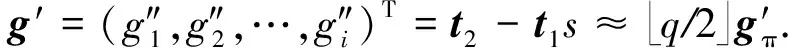
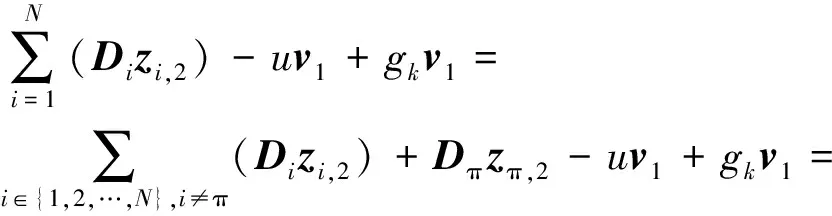
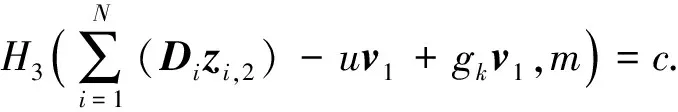
本方案的打开正确性得以满足.证毕.

定理2.完全匿名性.在DRLWEn,l,q,χ问题的假设下，本文的方案在随机预言模型中是完全匿名的.

证明.下面通过证明G0,G1,G2,G3一系列游戏的不可区分来证明本文方案的完全匿名性.

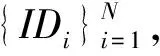
① 签名问询.输入任意明文m∈{0,1}*以及用户i，返回对应的签名Σ=((zi,1,zi,2)1≤i≤N,v1,t1,t2,t3)给A.

② 打开问询.A选择消息m∈{0,1}*及其对应的群签名Σ进行问询，如果Σ由群中用户j∈[N]合法产生，则返回用户j的身份信息，否则返回⊥.

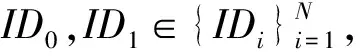
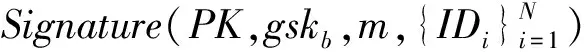
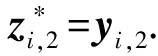
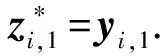
引理6.G1与G0在统计上不可区分.

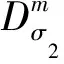
证毕.

引理7.G1与G2在统计上不可区分.

证明.与引理6证明同理可得G2与G1的距离在统计上是可忽略的.

证毕.

引理8.G3与G2在计算上不可区分.

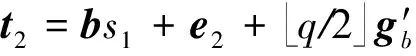
证毕.

G3可以看作是经过Naor-Yung变换[23]的LPR加密方案[24]，而该加密方案被证明是IND-CCA安全的.且G3中所得签名均由随机向量构成，所以A已无法从签名中得到任何有关用户IDb的信息.因此，可以计算出Pr[G3]=1/2+negl(n).由引理6～8可得，G0,G1,G2,G3在统计和计算上是不可区分的，因此得出A赢得G0的概率为Pr[G0]=1/2+negl(n)，即A攻破G0的完全匿名性的优势是可忽略的，而G0是挑战者C诚实执行本文方案后进行的交互游戏，因此A攻破本方案的完全匿名性的优势是可忽略的.

证毕.

定理3.不可伪造性.在RSISn,m,q,β问题的假设下，本文方案在随机预言模型下满足不可伪造性.

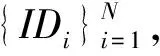
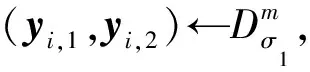
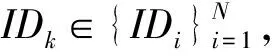
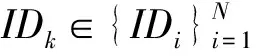
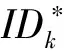
对上式化简可得

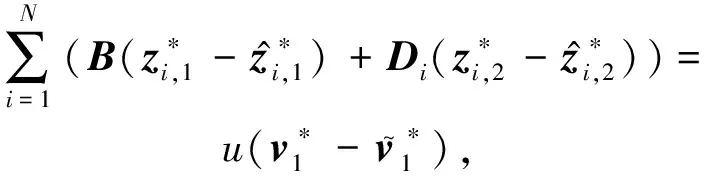
(1)

(2)

联立式(1)(2)后，得到

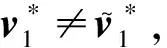
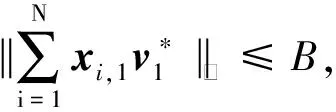
证毕.

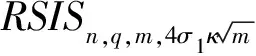
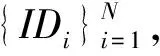
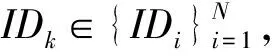
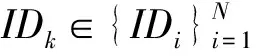
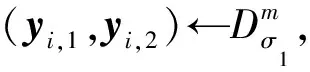
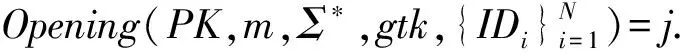
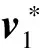
又由于A伪造的签名Σ*能够满足验证正确性，则有

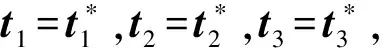
(3)

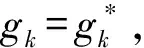
即

(4)

联立式(3)(4)可得

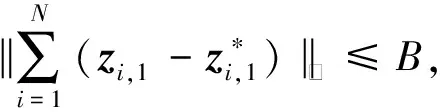
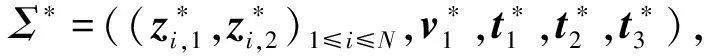
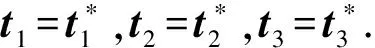
由于A伪造的签名具有验证正确性，满足

又因为Σ*能够被打开并追溯到j，所以有

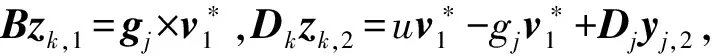
即Σ通过了验证算法和打开算法.

此时式(3)和(4)成立，联立可得

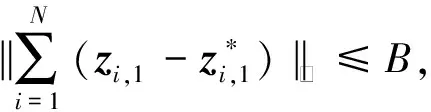
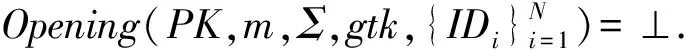
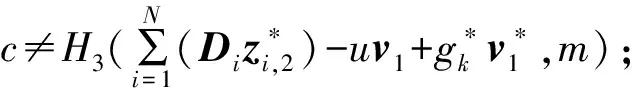
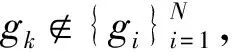
由于上述2种情况都能够通过验证算法，所以有

移项可得

综上所述，攻击者A若赢得完全可追溯性游戏，则C将求得上述RSIS问题的小整数解，但是在RSIS困难假设下求小整数解是困难的，因此攻击者A无法满足以上2个条件，所以本方案具有完全可追溯性.

证毕.

5 效率分析

选择4个现有的格上群签名方案与本文方案进行对比，分别是Libert等人[7]提出的没有陷门的对数大小的格上群签名、Ling等人[9]提出的基于格的完全动态群签名、Ling等人[11]提出的格上恒定大小的群签名以及Xu[26]提出的前向安全群签名.本文实验针对系统公钥长度、管理员追溯密钥长度、用户私钥长度、签名长度等指标进行对比.

表2为格上群签名在渐进效率方面的对比，其中n为安全参数，N=2为最大群成员个数.由表2可知，文献[7,9,26]的系统公钥、用户私钥以及签名的长度均与最大群成员个数N呈对数关系，而本文方案的和文献[11]方案的公私钥均为固定长度，仅与安全参数n相关.但注意到由于本文要实现的是基于身份的群签名方案，需要采用格基委派技术生成用户的私钥，进而造成所生成签名的长度与N呈线性关系；而其他方案虽然在签名长度方面或与N呈对数关系(文献[7,9,26])，或为固定长度(文献[11])，但它们均不具有基于身份的属性，存在公钥证书管理的负担.为了使比较结果更加直观，本文在保证所提方案满足安全性的前提下，选取了5组特定参数，即和N∈{256,512,1 024,2 048}，对4个方案的系统公钥长度、管理员追溯密钥长度、用户私钥长度及签名长度进行量化对比，比较结果列于表3.

Table 2 Comparison for the Asymptotic Efficiency of Group Signature表2 群签名渐进效率对比

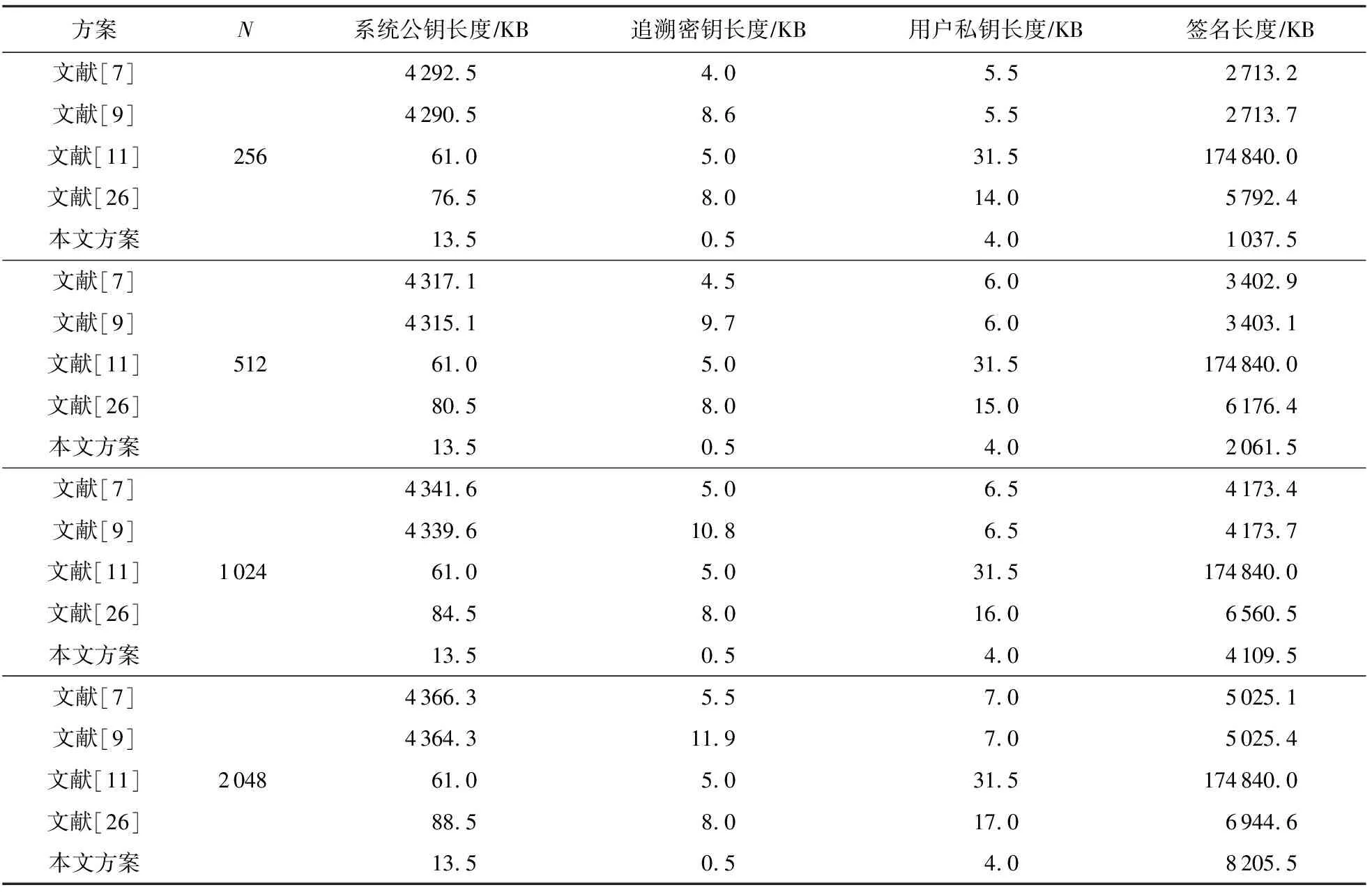
Table 3 Comparison for the Efficiency of Group Signature Under Different Number of Members表3 不同成员个数下的群签名效率对比

从表3可以看出，当安全参数n=512，最大群成员个数N∈{256,512,1 024,2 048}时，本文方案的公私钥长度在5个方案中最短，平均缩小了79.6%；当N≤1 024时，本文方案的签名长度在5个方案中仍为最短，平均缩小了57.3%；但当N=2 048时，本文方案的签名长度超过文献[7,9,26]的签名长度.综上所述，相较于文献[7,9,11,26]，本文方案的公私钥长度平均缩小了79.6%，签名长度平均缩小了39.9%.

另外，文献[7,9,11,26]的零知识证明系统存在健全性误差，在生成签名时均需要ω(logn)次的并行重复，而本文方案没有使用到零知识证明系统，仅调用1次拒绝采样算法即可实现签名.因此，与同类方案相比，本文方案具有较小的存储开销和计算开销，且更适用于小群组(例如N≤1 024)的场景.

6 结束语

相较于其他群签名，格上的群签名能够抵抗量子算法的攻击，格上基于身份的群签名能够避免复杂的用户公钥证书管理问题，可以有效地应用于匿名电子投票和电子商务系统等领域.本文基于RLWE和RSIS困难假设，在随机预言模型下提出了一个格上基于身份的群签名方案，并给出了详细的安全性证明.与已有的格上群签名方案相比，本文方案没有使用零知识证明，而是通过拒绝采样算法提高签名生成计算效率，密钥尺寸也相较其他方案更具优势，但签名长度与用户数呈线性关系，用户数N≥2 048时签名尺寸相对于其他方案较长.因此，下一步将考虑构造签名长度更短、运行效率更高的格上基于身份的群签名.

作者贡献声明：汤永利指导方案的整体设计、安全性分析以及论文撰写，把握论文整体创新性；李元鸿负责方案拟定、论文撰写以及效率分析；张晓航负责论文图表设计与规划，并参与了实验数据的整理；叶青负责把握论文创新性，并参与数学公式校对和方案效率分析.