基于盲源分离理论的超声回波信号消噪处理

郭北涛，张颢严，王 茹

(沈阳化工大学 机械与动力工程学院， 辽宁 沈阳 110142)

超声无损检测技术作为最具潜力的无损检测技术之一，凭借其便捷、高效、低成本、穿透性强、适用性广、对人体无害等优点，成为了工业产品质量控制和各类零部件安全监测的有效手段[1]. 随着工业生产水平的不断提高，常规的超声A扫描检测方式难以满足材料内部细小缺陷控制和检测效率的要求，超声C扫描可以弥补超声A扫描的不足，因此得到了发展。超声成像技术作为定量超声无损检测的方法之一，通过图像的形式将难以理解的缺陷特征信息直观地进行表征，使检测人员工作量减少同时也避免人为因素影响，提高检测结果的准确性[2-3]. 针对采集超声回波信号中存在干扰的情况，提出使用EEMD-PCA-FastICA方法对超声回波信号进行消噪处理。通过仿真分析验证了该方法的可行性，然后将该方法作用在实际采集的数据信号中，实现了噪声的去除，得到缺陷特征信息。

1 EEMD-PCA-FastICA算法的原理

结合EEMD和PCA的超声回波信号盲源分离方法(EEMD-PCA-FastICA)对实验采集的超声回波信号进行去噪处理，通过EEMD方法先将原始采集回波信号分为各阶IMF分量，再利用PCA方法进行源数目估计，用相关系数法将IMF分量信号重新构造及新观测信号构造，将观测信号的升维处理完成，以满足盲源分离的要求。最后使用FastICA运算处理新观测信号，提取出有效的信号频段。

1.1 EEMD算法的原理

经验模态分解(EMD)由N.E.Huang等人提出，用于分解非线性非平稳信号的自适应分解方法[4]. 为解决EMD分解中出现的模态混叠现象，Huang和Wu[5]提出了一种噪声辅助的EMD算法：集合经验模态分解(EEMD). 该算法的原理是将一定次数和比例的高斯白噪声加入到原始信号中，利用其频率均匀分布的特性，使原始信号极值点分布发生变化[6]，消除信号中的间歇性成分，使信号具有连续性，以达到改善模态混叠的效果。

EEMD具体分解步骤如下：

1) 将高斯白噪声pi(t)加入到原始信号x(t)中，得到综合信号：

Xi(t)=x(t)+pi(t)

(1)

式中,i为加入白噪声的次数，i=1,2,3,…,N.

2) 用EMD对信号Xi(t)分解，得到不同尺度IMF分量和剩余项ri(t)：

(2)

3) 重复步骤(1)、(2)n次，将分解得到的所有IMF分量一起取均值：

(3)

4) 综上所述，原始采集信号x(t)经由EEMD分解后，得到的最终结果为：k个IMF分量和一个剩余量：

(4)

1.2 PCA算法的原理

主成分分析(PCA)又叫主成分算法，其核心是利用降维思想进行数据降维[7]，它将原本较高维度的数据投射到低维度的子空间中，使得数据由n维降低到k维(n>k)，重新构建的低维空间能反映出数据的近似分布，且这k个维度之间满足两两相互正交、互不相关[8-9].

假设原始数据集的矩阵为：

(5)

其中，m表示数据集中含有的数据样本个数，n表示原始数据含有的特征数，且每一行代表一个数据样本。

PCA算法步骤如下：

1) 去均值标准化。

将原始信号数据做出预处理，算出每个特征的均值，接着将数据样本中每一个特征都减去自身均值。标准化的目的是为了降低不同数量级的影响。

(6)

其中，zij为标准化以后的值；xij为原始数据集矩阵X中的第i行第j列元素。

标准化矩阵Z：

(7)

2) 求协方差矩阵C.

均值标准化处理后，由协方差计算公式得到由m个样本在n维特征下的协方差矩阵C：

(8)

3) 特征值及特征向量的计算。

根据特征方程：

|λE-C|=0

(9)

求特征值λi(i=1,2,3,…,n)和特征向量ai. 将λi由小到大进行排列，依λi的次序将特征向量进行相同排序得到特征向量矩阵A.

A=(a1,a2,a3,…,an)

(10)

4) 降维计算。

要实现对原始数据进行降维，要确定主成分的个数。选择的主成分总共累计应具有原始信号90%以上的信息量，即累计贡献率G≥90%，其计算公式如下：

(11)

其中，p表示选择主成分个数。

根据计算结果，提取特征向量矩阵A中满足条件的主成分(即前p列向量)，得到降维矩U：

U=(a1,a2,…,ap)

(12)

5) 降维后的数据。

把原始数据矩阵X投射到降维矩阵上。得到数据矩阵W：

W=XU

(13)

PCA算法主要应用于数据信号的降维处理，去除原信号中没有区分性，贡献小的元素。实验在EEMD分解的基础之上，重组信号，使用PCA算法求解协方差矩阵的特征值，以累计贡献率≥90%为依据来预估源信号数目。

1.3 FastICA算法介绍

快速独立成分分析(FastICA)算法是独立成分分析中常用的方法,由最大非高斯性推理而来,可以实现快速迭代的算法，它具有鲁棒性强，分离好，收敛快等优点，能够快速地将相互独立的源信号从观测信号中分解开来[10].

FastICA算法的步骤可以总结为：

1) 将观测信号做出中心化与白化处理。

2) 初始化分离矩阵W.

3) 利用迭代公式更新矩阵W.

4) 归一化处理。

5) 判断是否收敛，若收敛继续下一步，不收敛转到第(3)步。

6) 得到W，带入Y=WX求解出源信号S的最大程度逼近信号。

在快速独立成分分析过程中首先得到分离矩阵，再对混合信号进行迭代计算实现盲源分离，得到源信号。

2 EEMD-PCA-FastICA算法仿真分析

2.1 仿真信号构建

为了检验该算法的有效性，依据该算法原理在MATLAB平台进行仿真模拟实验。选取3组模拟信号进行仿真实验，采样频率设为1 000 Hz，采样点个数为500，模拟信号h1(t)、h2(t)、h3(t)分别表示为：

h1(t)=1.3cos(350t+10)

h2(t)=1.5sin(80t)

(14)

h3(t)=[1+0.6sin(30t)]sin(900t)

为了得到随机混合模型，通过随机矩阵K=(0.793, -0.976, 1.397)对3组模拟信号进行组合，得到仿真观测信号H. 组合方式如下：

(15)

模拟信号h1(t)、h2(t)、h3(t)以及仿真观测信号H的时域图和经过快速傅里叶变换得到的频谱图,见图1.

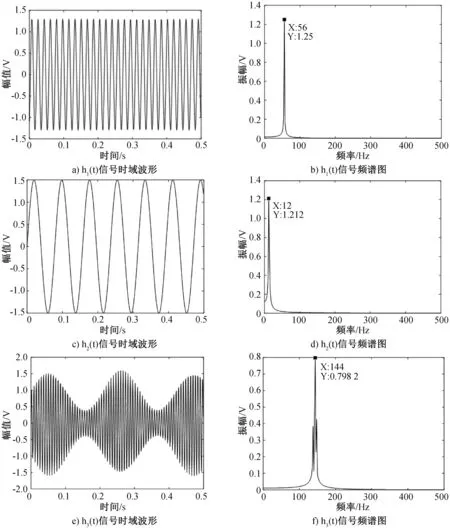
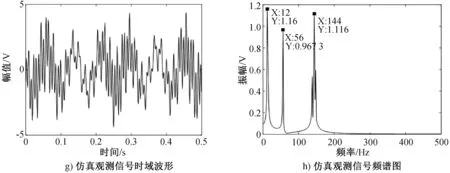
图1 模拟信号及仿真观测信号的时域图和频谱图

由于仿真观测信号数目为1，而模拟源信号个数为3，观测信号数目与源信号数目之间的关系不满足约束条件，即存在盲源分离欠定问题。

2.2 EEMD分解及源数目判定

先用EEMD对信号进行分解，结果见图2，得到7个频率由高到低的IMF分量以及1个剩余项res.

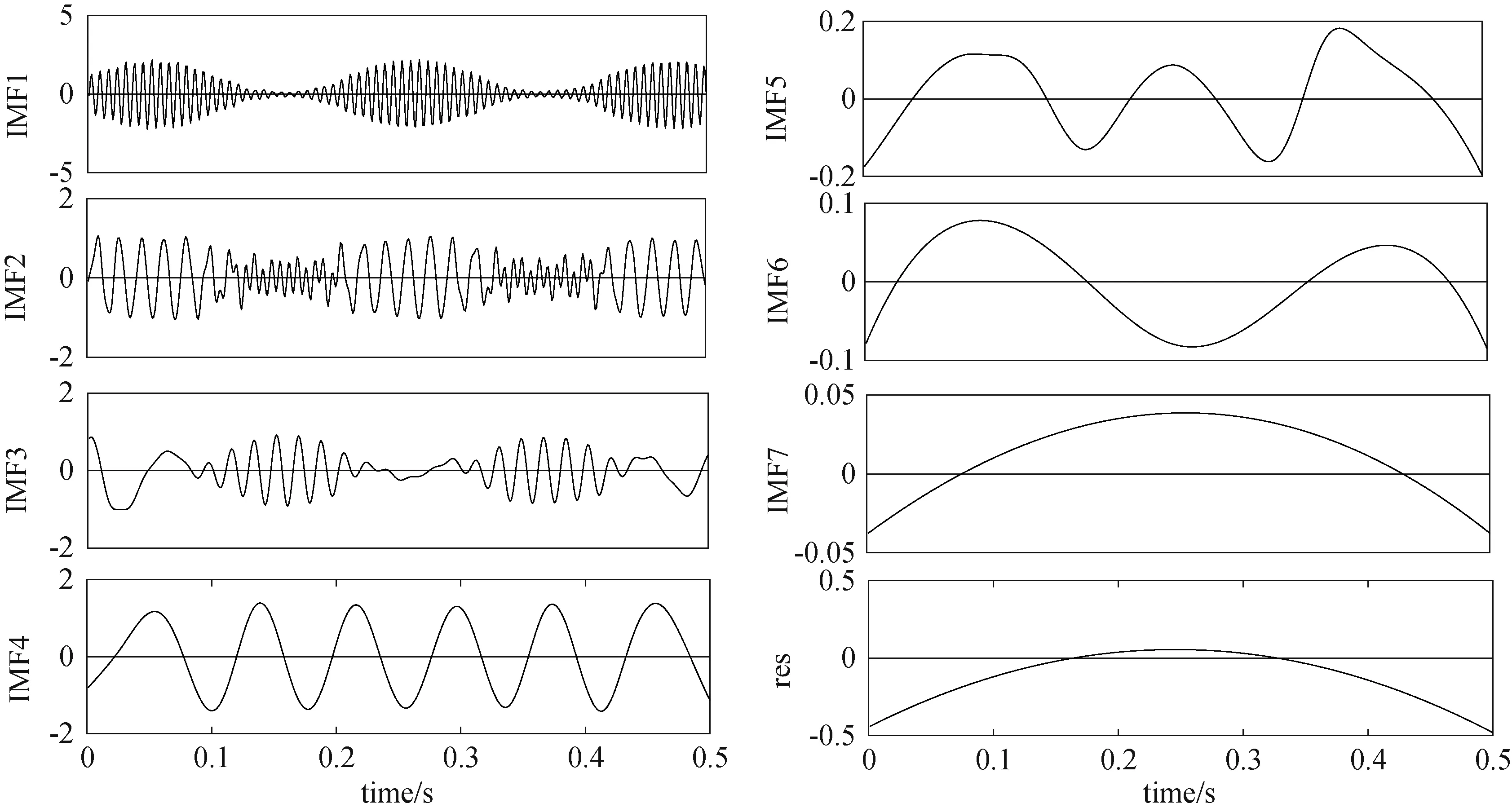
图2 EEMD算法分解结果图

将经过EEMD分解后的各阶IMF分量与观测信号组成多维数据信号，利用PCA算法估计源信号数目。依据PCA算法求解出各阶IMF分量的特征值，见表1，以其特征值的累计贡献率>90%为基准，判断出源信号数目为3，与实际源信号数目一致。

表1 重构矩阵的特征值表

2.3 新观测信号构建

计算IMF分量与仿真观测信号的相关系数值，得到相关系数阈值T的值，比较阈值与相关系数的大小，并以此为判断准则重构IMF分量。利用重构信号同原始采集超声回波信号构建新的虚拟观测信号，并使其维度与估计的源信号数目保持一致。

求解原始超声回波信号与分解出的各个IMF分量之间的相关系数Rj，将相关系数标准差作为判断阈值，记作T.

相关系数计算公式如下：

(16)

式中，R为相关系数；y为原始超声回波信号；n表示信号的总长度；c为经EEMD分解后的IMF分量。

阈值计算公式为：

(17)

其中：Rj表示原信号与第j个IMF分量的相关系数；T为阈值。

通过式(15)计算各阶IMF分量与仿真观测信号的相关系数值，计算结果见表2. 由式(16)解得阈值T=0.329 9.

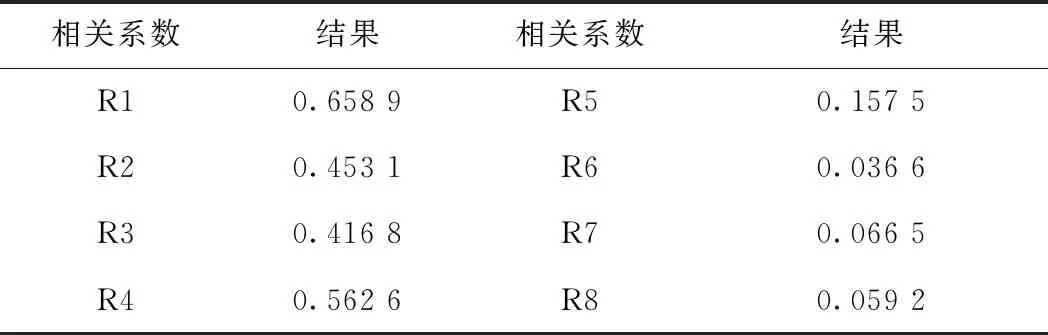
表2 IMF分量的相关系数表

将表2中各个IMF分量的相关系数与阈值进行比较，依据相关系数值与阈值的大小关系进行IMF分量的重构。将重构后的信号与仿真观测信号组合成新的多维观测信号，并且新的多维观测信号维数等于源信号数量，即等于3，确定观测信号与源信号之间的对应关系。

2.4 仿真结果与分析

最后将新观测信号作为FastICA算法的输入，进行解混处理。得到3个分离之后的独立分量，分离后各信号的时域图和经快速傅里叶变换得到的频谱图见图3.

对比分离前后信号的频谱图可知，3个仿真模拟信号频谱图中峰值频率分别为：56 Hz、12 Hz、144 Hz；3个分离信号频谱图中峰值频率分别：12 Hz、56 Hz、144 Hz. 由此可知,分离前后信号排列顺序虽然发生了变化，但是相对应的信号在频域上频谱峰值频率保持一致，故源信号中的频域特征被很好保留下来。

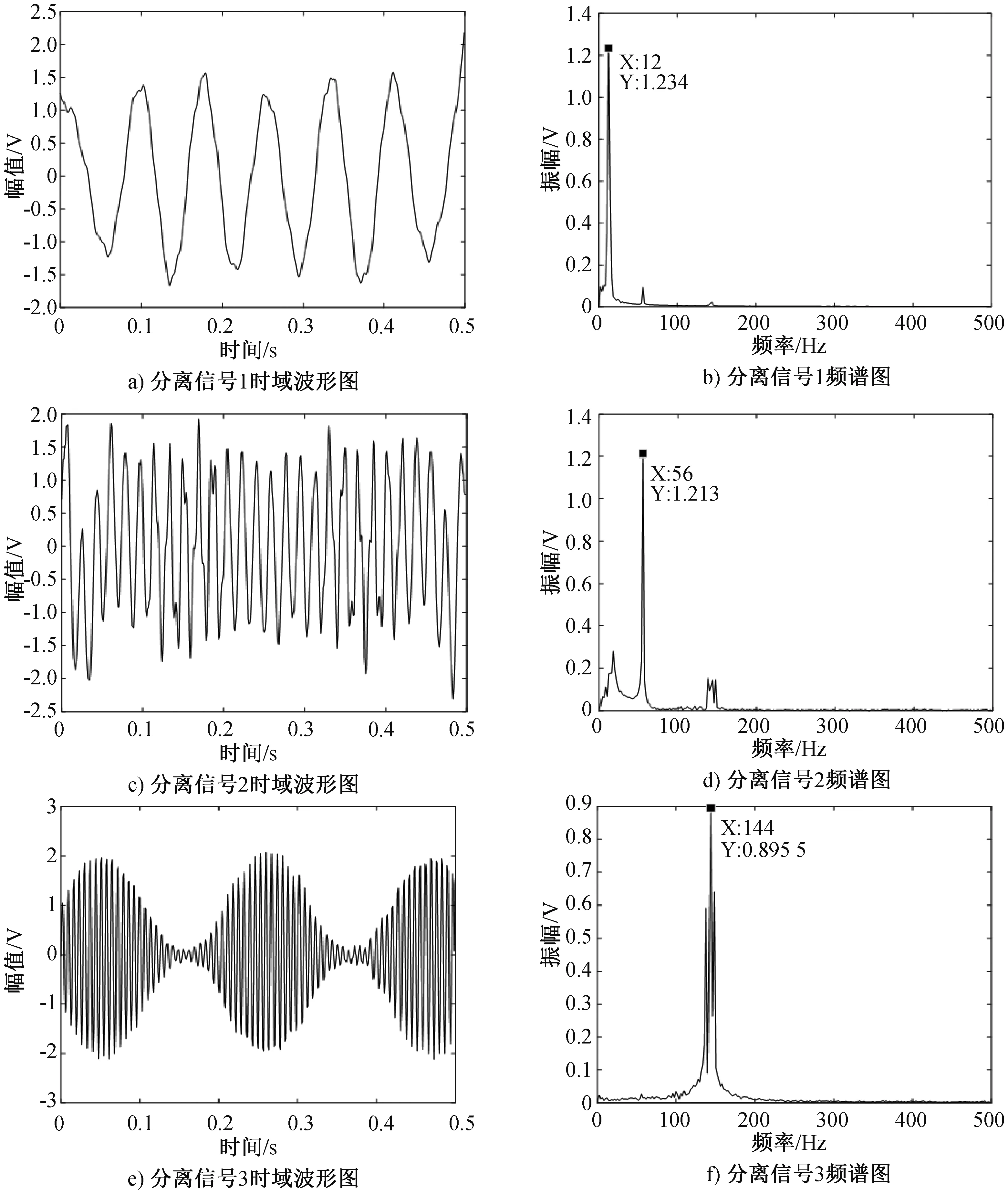
图3 各个分离信号的时域波形和频谱图

3 实验环境

整个超声C扫描成像实验系统是由机械扫查模块、运动控制模块、超声信号检测与处理模块组成。机械扫查模块主要由自动扫查桁架机械手、水箱平台、超声探头装置等组成。水箱保证了实验过程中满足良好的水耦合条件。超声探头装置确保超声探头的位置可调，其上端的固定板对整个探头装置起固定作用，下端的夹具夹持超声探头使探头的中心轴线与扫查面垂直。运动控制模块主要由PLC、位置传感器、电机等器件构成。信号检测模块保证了超声信号的发射接收，信号的调理等功能的实现，并将超声模拟信号进行A/D转换后，由上位机分析处理实现C扫描成像。实验中选用广东汕头超声电子公司生产的5P20规格超声水浸聚焦直探头(图4)，采用超声水浸聚焦检测法。在超声检测中以水作为耦合剂，具有价格低、对环境无污染、浸润性能良好等优点。

图4 5P20超声直探头实物图

4 EEMD-PCA-FastICA算法在实验数据中的应用

为了进一步验证所提出的EEMD-PCA-FastICA方法对于超声回波信号去噪的有效性，采用实验搭建的水浸超声C扫描成像系统进行超声扫查，提取出被检工件内部缺陷处瞬时超声A扫回波信号时域波形图和经FFT后得到的频谱图，见图5，同时以MATLAB软件平台为工具将提取的超声A扫信号进行EEMD-PCA-FastICA分离，分离后的信号见图6.

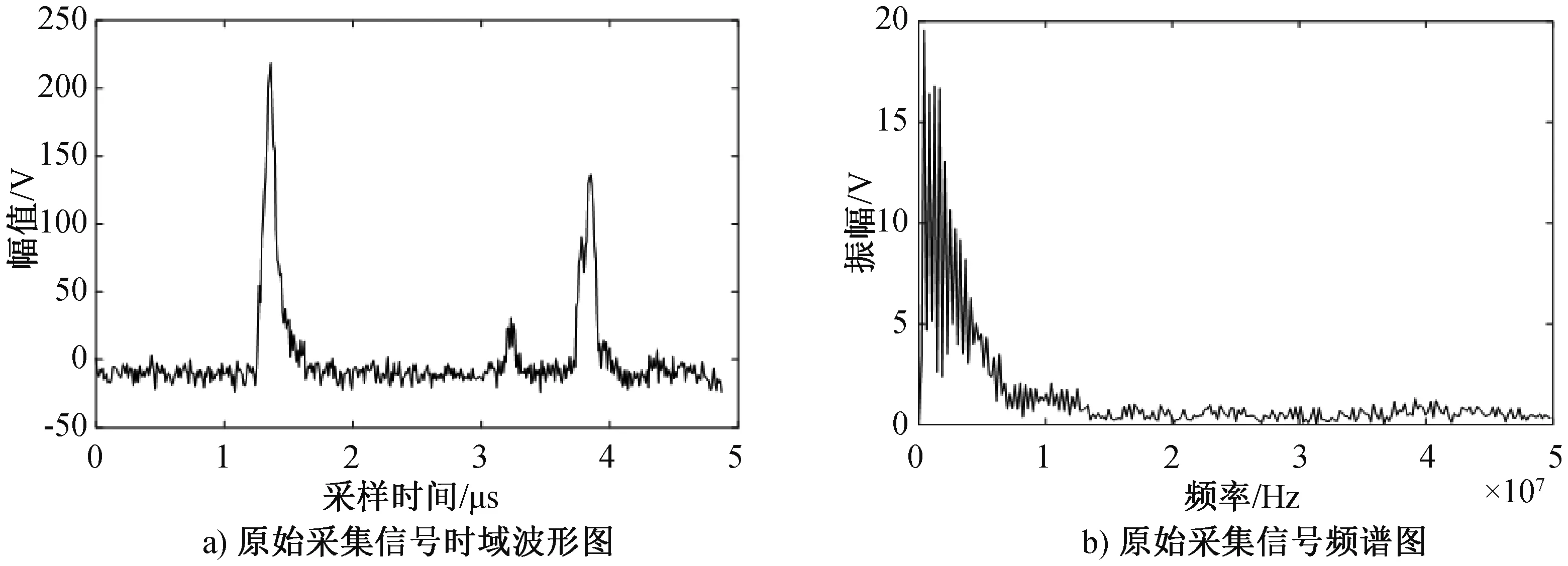
图5 被检工件缺陷处采集回波信号图

图6 回波信号去噪分离结果图

同时对比图5b)和图6b)，在频域波形中，分离前后低频部分的频谱分布基本保持一致，主频信息得到保护，而高频噪声信号部分基本完全去除。进一步表明了该方法对噪声信号滤除的有效性，并且使得有用信号的频域特征得到了很好的保留。

综上所述，EEMD-PCA-FastICA方法能对超声回波缺陷特征信号中混杂的噪声信号进行有效的分离，去噪效果良好。

5 结 论

对系统采集的超声脉冲回波信号存在的噪声问题进行基于EEMD和PCA的盲源分离处理。通过EEMD算法与PCA算法相结合，进行新观测信号的重构，确定了源信号与观测信号之间的对应关系，并对新观测信号进行FastICA处理，得到有效信号频段。实验中通过对比回波信号进行EEMD-PCA-FastICA分离前后的时域波形图可知，分离前的超声A扫回波信号中混杂了大量噪声信息，难以对被检工件进行准确的辨别和分析；而经过消噪处理后的信号波形更加清晰，波峰处突出，可以明显地辨别出缺陷特征信号，这说明了该方法具有较好的去噪效果。综上经仿真分析和实验验证表明，该方法具有良好的消噪效果，能很好地分离出缺陷特征信息。