高温高湿巷道内不稳定换热系数影响因素分析及模型建立*

杜翠凤，杜 帅，王九柱，王 远，晋伟博

(北京科技大学 土木与资源工程学院，北京 100083)

0 引言

随着矿山行业不断向深部开采，深部开采问题逐渐显现出来，其中，矿井热害是金属矿山深部开采过程中常见灾害[1]，矿井深部巷道由于开采深度深，长期处于温度为30 ℃以上的高温环境、相对湿度为80%～95%的高湿环境，在此工作环境下，员工工作效率降低，容易引发安全事故。改善井下高温高湿环境，大多数情况采用人工制冷降温的方式，确定制冷量的多少，需要计算井下热负荷、预测风流温湿度，而研究高温、高湿环境不稳定换热系数的变化规律是热负荷计算和风流预测的关键。

目前，国内外针对矿井高温高湿环境下热湿交换和不稳定换热系数研究，主要从理论推导、数值计算、相似实验3个角度进行探究。在理论推导方面，孙培德[2]通过引入地温场系数，利用拉普拉斯变换推导出不稳定换热系数的计算式;岑衍强等[3]提出无因次不稳定换热系数；何昌富等[4]利用分离变量法，推导不稳定换热系数的理论解；杨威等[5]考虑水分蒸发，将水分蒸发需热量表示成巷道出口风流理论温度与实际温度之差的显热交换量进行风流换热研究；王红兵等[6]利用分离变量法求解出不稳定换热系数理论计算式和简化计算式。在数值计算方面，王天明[7]利用Matlab编写仿真软件，得到水分蒸发对风流温度影响很大；李宗翔等[8]、Li等[9]利用Matlab模拟矿井风流温湿度变化，并修正水分蒸发影响下对流换热系数；张一夫等[10]通过数值计算，将围岩内部导热与围岩和风流热湿交换问题耦合；Li等[11]通过建立热湿耦合模型，将围岩内部传导、非等温流动以及水分蒸发进行耦合模拟；吴星辉等[12]利用Comsol软件对围岩与风流的换热进行模拟。在相似实验方面，杨高飞[13]通过相似模拟实验研究井下围岩与风流之间的热湿交换；赵旭光[14]利用水平管路实验台，得出多种情况下对流传热系数的关联式；娄志鹏[15]通过构建巷道隔热结构模型，确定围岩传热相关系数以及巷道隔热结构热量释放的计算方法；王长彬[16]对进出口温度变化特性及围岩传热系数变化特性进行研究；李宗翔等[17]提出构建淋湿巷道风流换热系数模型，修正围岩与风流的换热系数；周少柳[18]根据现场实测数据得到围岩与风流的不稳定换热系数；侯江丽[19]确定在不同换热条件下壁面和风流之间的换热系数；高佳南等[20]用风温、风速、潮湿率、巷道尺寸、巷壁温度、热物性及摩擦阻力系数等可测参数表述对流换热系数。

由于井下环境复杂，理论推导很难将各种因素考虑在内，相似实验存在诸多因素限制。因此，通过数值模拟研究高温、高湿环境巷道内的传热传质问题。针对刚开掘的深井巷道，以其高温高湿的巷道环境为背景，通入相对湿度为95%的新鲜风流，考虑壁面存在水膜且水膜发生水分蒸发的情况，利用Fluent数值模拟软件开展模拟实验，研究各因素对不稳定换热系数的变化规律的影响。

1 模型建立及参数设置

1.1 模型建立

1.1.1 物理模型

如图1所示，为物理模型，巷道为拱形结构，宽2.40 m，直墙高2.85 m，拱高4.05 m，长度为500 m，围岩厚度为15 m。研究当量直径对不稳定换热系数的影响时，通过改变巷道宽度来实现当量直径的改变。

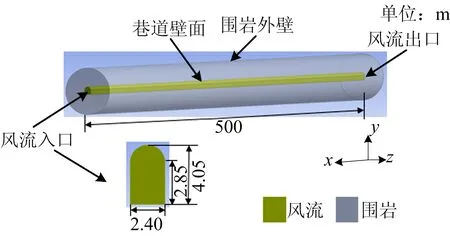
图1 物理模型Fig.1 Physical model

1.1.2 数学模型

风流在巷道内部的流动遵守连续性方程、动量守恒方程、能量守恒方程和组分运输方程。由于传热传质的复杂性，对风流与围岩的换热过程做出如下假设：

1)围岩为均匀介质，岩石密度、导热系数、比热容等热物理参数均以常数处理。

2)模拟过程中流体的密度、导热系数、比热容等物理参数均以非线性处理。

3)巷道换热过程不考虑由于围岩产生的辐射换热。

4)在初始时刻围岩与巷道内部温度相同。

基于以上假设建立连续性方程如式(1)所示：

(1)

式中：ρ为气体密度，kg/m3；t为时间，s；ux为流体在x方向上的速度，m/s。

动量方程如式(2)所示：

(2)

式中：uy为流体在y方向上的速度，m/s；p为流体相压力，Pa；τxy为应力张量；gx为x方向上的重力加速度，m/s2；Fx为颗粒在x方向上的流体阻力，N。

能量方程如式(3)～(5)所示：

(3)

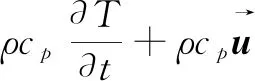
(4)

q=-λ∇T

(5)

风流在流动过程中属于湍流，选择κ～ε湍流模型。其中湍流动能κ及其耗散率ε由式(6)～(7)得到：

(6)

(7)

式中：κ为湍动能，J；Gκ为湍动能κ的产生项；ε为湍动能κ的耗散项，m2/s2；Sε,Sκ分别为湍动能的耗散率和湍动能源项；μ为动力黏性系数；μt为湍动黏度，μt=ρCμκ2/ε；C1ε,C2ε,Cμ,σε,σκ是经验常数，分别取值为1.44，1.92，0.09，1.3，1.0。

井下巷道处于高温高湿环境，且流入的新鲜风流含湿量比较高，流体为干空气和水蒸气混合的湿空气，采用组分运输方程，控制风流的含湿量和空气中水分扩散，如式(8)～(9)所示：

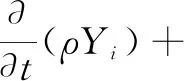
(8)

(9)

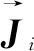
1.2 网格划分

采用Mesh板块对物理模型进行网格划分，模型网格划分结果如图2所示，网格形状为六面体，网格数量为508 014，网格平均质量为0.92。

图2 网格划分示意Fig.2 Schematic diagram of meshing

1.3 参数设置

通过Fluent数值模拟软件模拟围岩与风流之间的热湿交换过程，其中，巷道内的潮湿壁面通过Discrete Phase模型中的Droplet蒸发模型，实现水分蒸发过程。巷道壁面设置为耦合换热，巷道壁面粗糙度高度设置为0.07 m,粗糙度常数设置为0.5，围岩外壁设为恒定壁温。风流入口处选择速度入口，风流出口选择压力出口。模拟过程中各具体参数设置如表1所示。

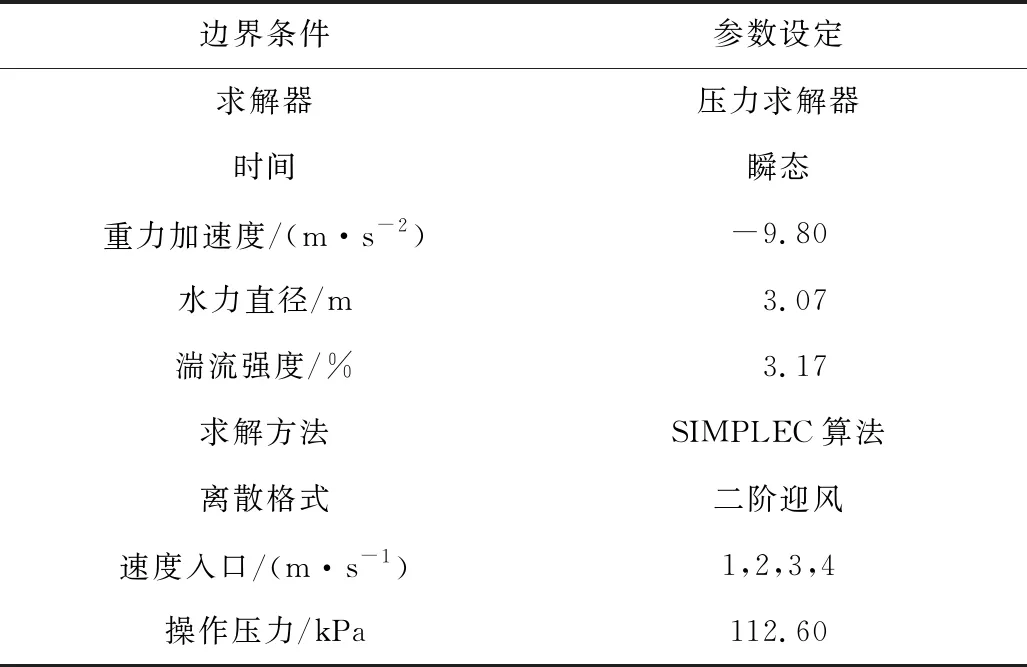
表1 参数设置Table 1 Parameters setting

1.4 模型验证

为验证数值模拟结果的可行性，首先在不考虑水分蒸发的情况下进行数值模拟，利用岑衍强[3]提出的不稳定换热系数的计算公式，如式(10)所示，通过该公式计算与Fluent数值模拟结果进行对比分析。

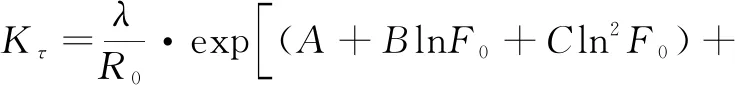
(10)

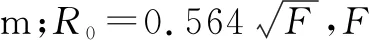
当∞>F0≥1时，A=0.020 01;B=-0.299 841 3;C=1.597 64×10-2；A′=-1.061 628;B′=0.136 679 4;C′=-9.702 536×10-3。

当1>F0>0时，A=2.409 134×10-2;B=-0.314 263 4;C=1.469 856×10-2；A′=-1.063 224;B′=0.151 002 4;C′=-1.625 136×10-2。

理论计算与Fluent数值模拟结果对比如图3所示，由图3可知，理论值和模拟值差异较小，其中，最大误差仅为5.76%，表明理论值和模拟值吻合度较高，数值模拟结果可靠。

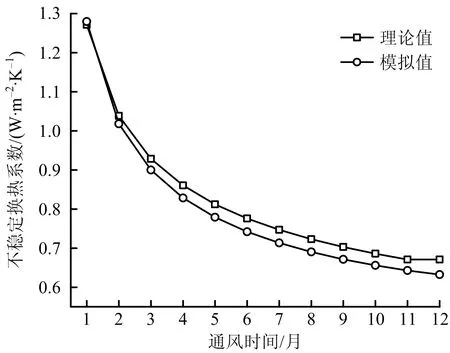
图3 不稳定换热系数的理论值和模拟值的对比Fig.3 Comparison between theoretical and simulated values of unstable heat transfer coefficient

2 不稳定换热系数影响因素分析

2.1 不稳定换热系数随时间的变化规律

时间对不稳定换热系数的影响如图4所示，由图4可知，不稳定换热系数与通风时间呈负相关，随着通风时间的增长，巷道壁面的不稳定换热系数逐渐降低，最后趋于稳定。通风时间主要是通过改变通风总体积的量从而影响不稳定换热系数的值，通风总体积等于通风速度乘以通风面积乘以通风时间。随着通风时间的增长，通风总体积的量增大，风流不断将围岩散发的热量带走，围岩被冷却，围岩近壁面温度与风流近壁面温度接近，温度差减小，壁面向风流散发的热量减小，继而导致巷道壁面的不稳定换热系数的降低。此外，通过高温高湿巷道和普通巷道对比发现，高温高湿巷道不稳定换热系数随时间的变化规律与普通巷道一致，均是随通风时间的增加而降低。在通风1个月时，高温高湿巷道不稳定换热系数比普通巷道增加了13.3%，在通风时间为1 a时，高温高湿巷道不稳定换热系数比普通巷道增加了12.5%。

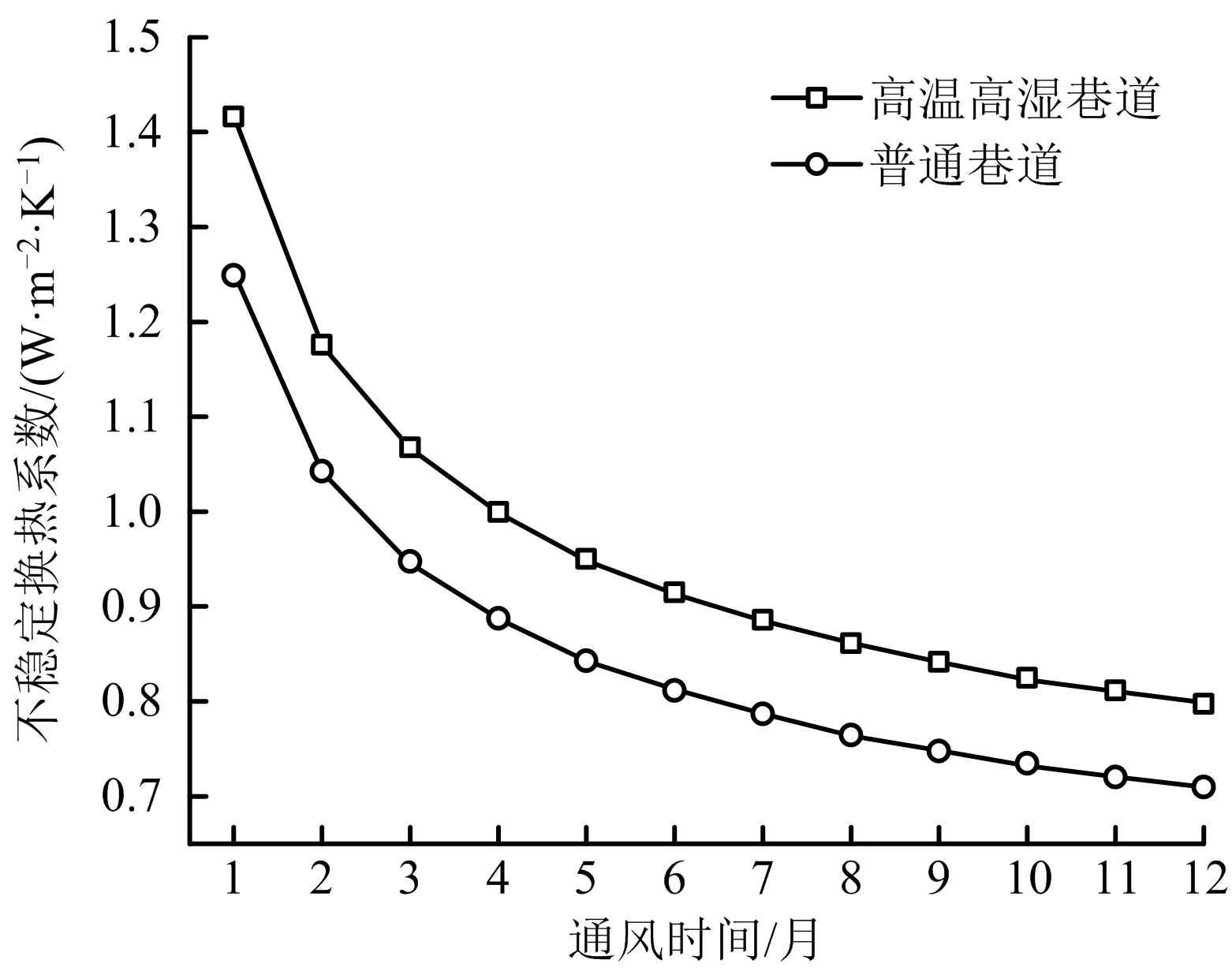
图4 不稳定换热系数随时间的变化规律Fig.4 Variation Law of unstable heat transfer coefficient with time

2.2 不同影响因素下不稳定换热系数变化规律

根据岑衍强等[3]对不稳定换热系数的计算公式，选择入口风流温度、风流速度、岩石导热系数、原岩温度以及巷道当量直径作为研究变量，利用Fluent数值模拟软件进行单因素实验，以风流温度293 K，风流速度2 m/s，大理岩导热系数，原岩温度313 K以及当量直径3.07 m为基础参数，研究某一因素对不稳定换热系数的影响时，其他因素为以上基础参数。巷道初始温度与原岩温度相同，初始湿度为95%，模拟高温高湿的初始巷道环境，在通入新鲜风流之后，研究不稳定换热系数的变化。另外，通风时间主要通过控制通风总体积来影响不稳定换热系数，在研究其他因素对不稳定换热系数影响的时候，应保持通风时间或者通风总体积一定。

1)风流速度

速度对不稳定换热系数的影响如图5所示，研究速度对不稳定换热系数的影响，需保证通入新鲜风流的总体积相同。由图5可知，在通风总体积一定的条件下，不稳定换热系数与速度呈正相关，入口速度越大，巷道壁面的不稳定换热系数越大。新鲜风流不断从巷道入口进入，当风流的速度越大时，围岩与风流之间的对流换热程度越深，通风总体积一定的条件下，风流带走的热量越多，围岩散热量大；另外，风流速度越大，巷道壁面处水分蒸发越剧烈，水分蒸发所吸收的热量越多，围岩散热量越大。所以，风流速度越大，巷道壁面的不稳定换热系数越大。

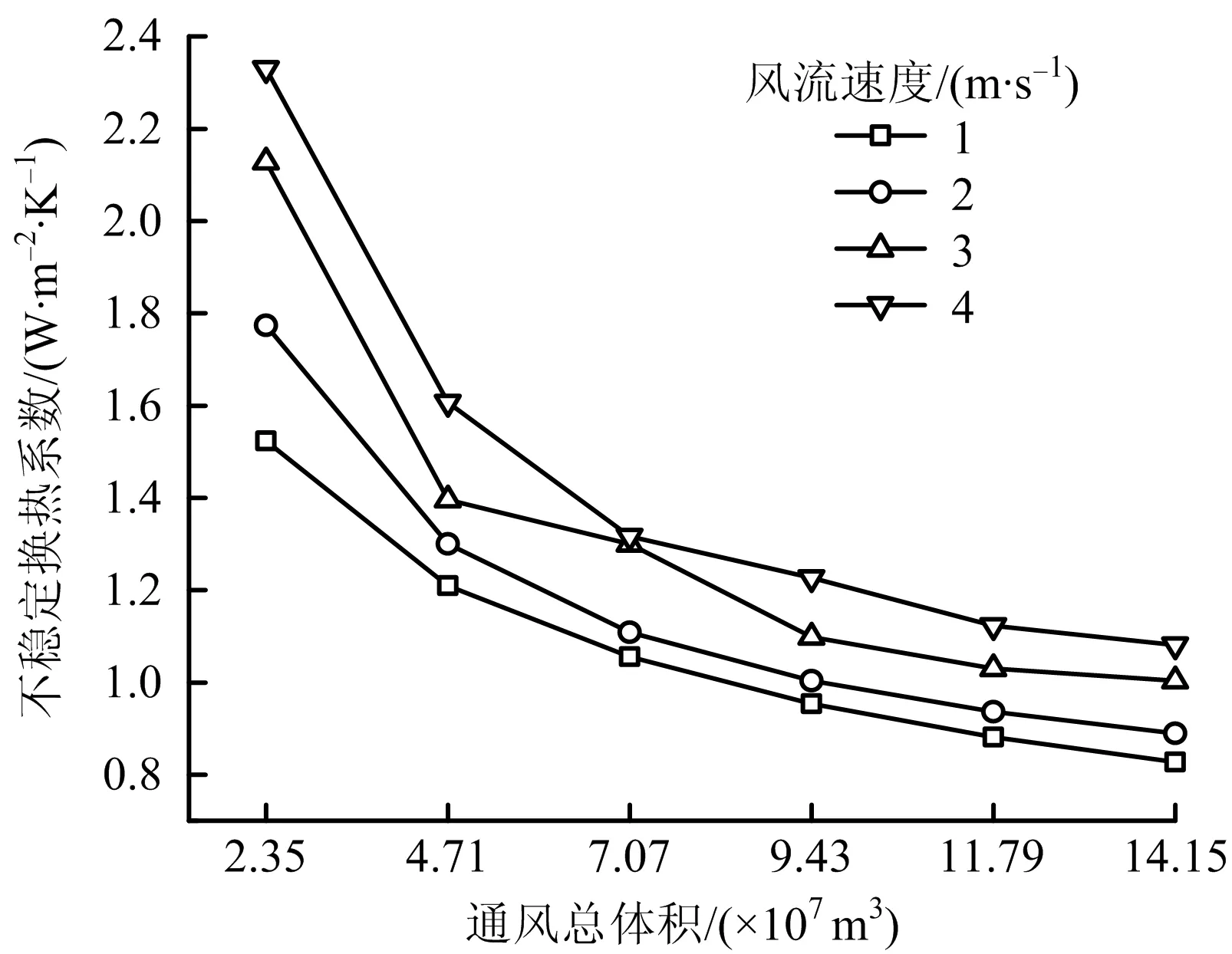
图5 速度影响下不稳定换热系数随通风总体积的变化规律Fig.5 Variation law of unstable heat transfer coefficient with total ventilation volume under influence of velocity

2)风流温度

风流温度对不稳定换热系数的影响如图6所示，由图6可知，入口风流温度的大小对于不稳定换热系数的影响较小，不同风温下不稳定换热系数并没有明确区分，其值很接近。改变入口风流温度，直接会改变围岩与风流之间的温度差，温度差决定围岩散热量的多少，当围岩与风流温差增大时，围岩散热量增加，但在计算不稳定换热系数时，热通量与温差成倍数增加，所以不稳定换热系数的值接近。另外，风流温度改变会影响空气的传热性质，当空气传热性质改变以后，空气在单位时间内所能接收的热量就会发生变化，由于温度改变幅度较小，空气传热性质接近，对空气所能接收的围岩散热量的影响较小。

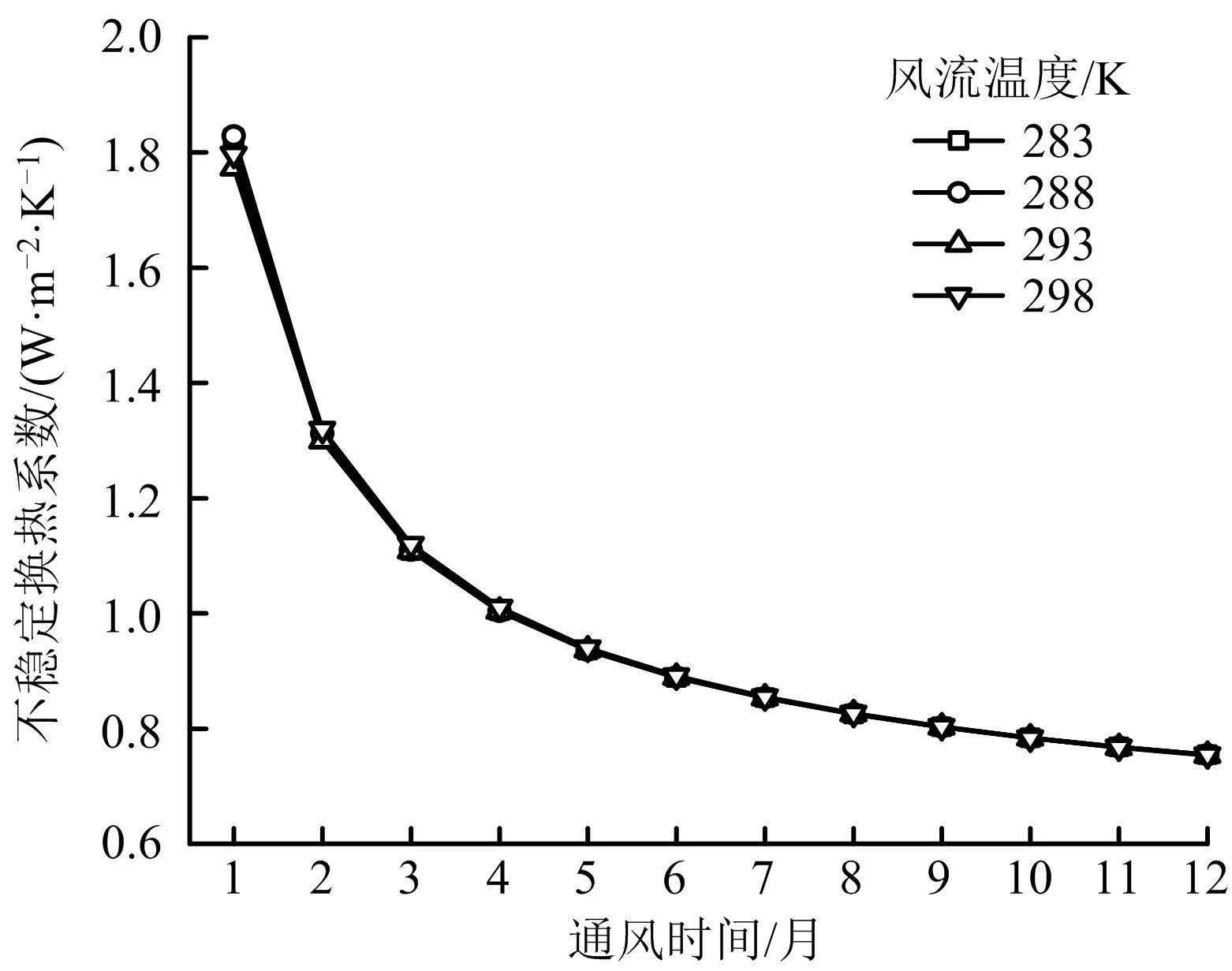
图6 风流温度影响下不稳定换热系数随时间的变化规律Fig.6 Variation law of unstable heat transfer coefficient with time under influence of air flow temperature

3)岩石导热系数

岩石导热系数对不稳定换热系数的影响如图7所示，其中石灰岩、花岗岩、大理岩、石英岩的导热系数分别为2.04，2.50，2.91，5.53 W/(m·K)。由图7可知，不稳定换热系数与岩石导热系数呈正相关，不稳定换热系数随着岩石导热系数增大而增加。这是因为岩石导热系数越大，单位时间内从围岩深部向巷道壁面传递的热量就越多，因此围岩的热通量增大，导致不稳定换热系数增大，所以岩石的导热系数越大的矿井，巷道内部温度相对会越高。

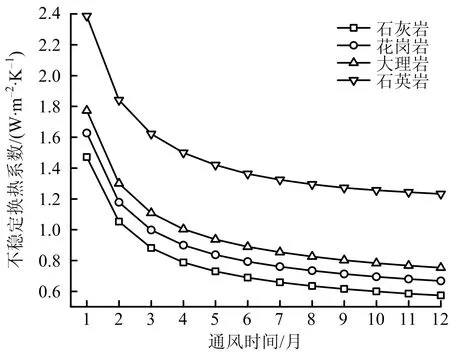
图7 岩石导热系数影响下不稳定换热系数随时间的变化规律Fig.7 Variation law of unstable heat transfer coefficient with time under influence of rock thermal conductivity

4)原岩温度

原岩温度对不稳定换热系数的影响如图8所示，由图8可知，原岩温度对于不稳定换热系数的影响较小，不同原岩温度下不稳定换热系数的值接近。改变原岩温度，直接会改变围岩与风流之间的温度差，温度差决定围岩散热量的多少，原岩温度增大，单位时间内围岩散热量增多，即围岩热通量增大，在计算不稳定换热系数时，热通量与温差成倍数增加，所以不稳定换热系数的值接近。另外，原岩温度通过温度的改变来影响岩石的热物理性质，温度增加，岩石的导热性能增大，上文做出假设围岩热物理参数为常数，所以围岩温度改变对热物性的影响忽略。如果只考虑温度差对不稳定换热系数影响，则不稳定换热系数变化不明显。

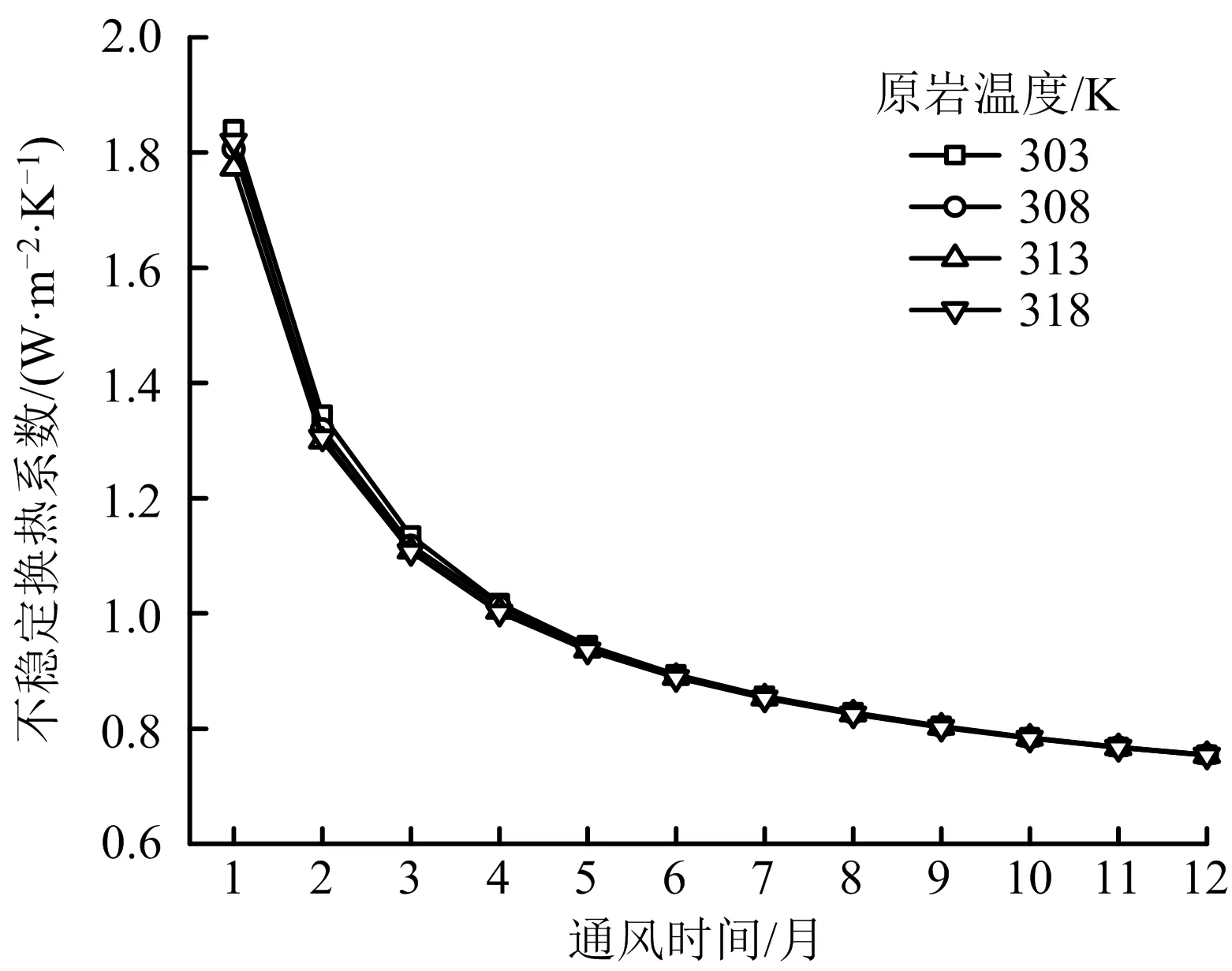
图8 原岩温度影响下不稳定换热系数随时间的变化规律Fig.8 Variation law of unstable heat transfer coefficient with time under influence of raw rock temperature

5)巷道当量直径

当量直径对不稳定换热系数的影响如图9所示。由图9可知，在通风总体积一定的条件下，巷道当量直径与不稳定换热系数之间呈正相关，不稳定换热系数随着巷道当量直径增大而增大。巷道当量直径增大，巷道壁面与风流的接触面积增大，导致巷道壁面水分蒸发的量增多，水分蒸发所吸收的热量增大。所以，巷道当量直径越大，巷道壁面的不稳定换热系数越大。

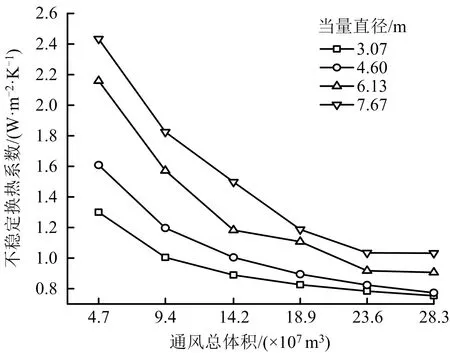
图9 当量直径影响下不稳定换热系数随通风总体积的变化规律Fig.9 Variation law of unstable heat transfer coefficient with total ventilation volume under influence of equivalent diameter

3 不稳定换热系数计算模型建立

3.1 正交实验方案设计

为验证各因素对不稳定换热系数的影响程度，探究各因素与不稳定换热系数之间的关系。本文利用正交实验进行定量分析，针对风流速度、风流温度、岩石导热系数、初始岩温、当量直径5个因素，分别取4个水平进行正交实验设计，取通风时间为1个月时的不稳定换热系数为评价标准，因素水平表和正交实验结果如表2～3所示。

表2 因素水平Table 2 Factors levels

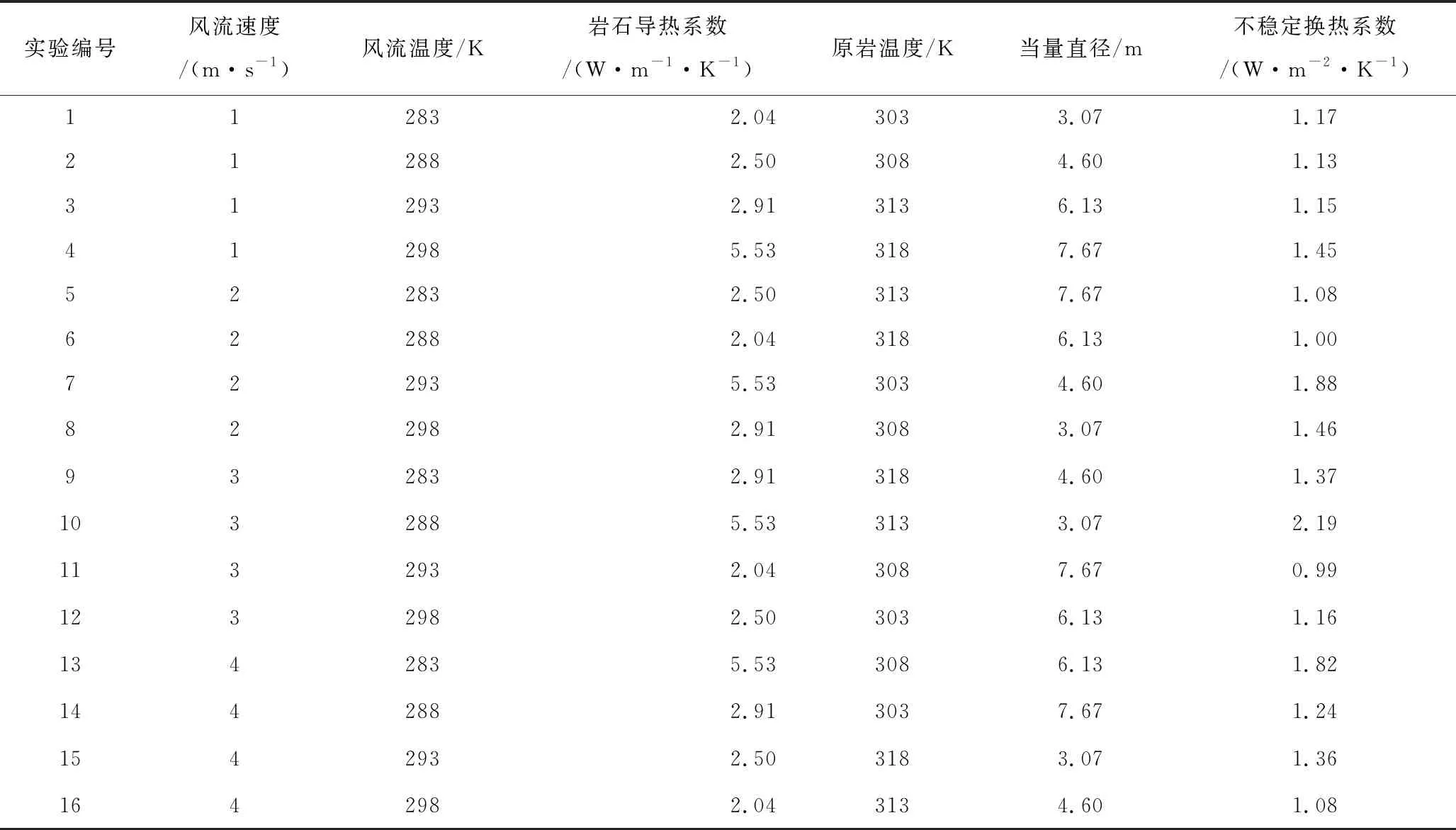
表3 正交实验方案及结果Table 3 Orthogonal experimental scheme and results

利用正交实验的结果，进行极差分析，以1个月的不稳定换热系数的结果为评价指标的极差分析结果如表4所示。

由表4可知，岩石的导热系数对应的极差值为0.775，对不稳定换热系数的影响程度最为显著；巷道当量直径对应的极差值为0.355，对不稳定换热系数的影响仅次于岩石导热系数；风流速度对不稳定换热系数有一定影响，但不如导热系数和当量直径影响程度大；原岩温度和风流温度对巷道壁面不稳定换热系数的影响较小。

表4 极差分析结果Table 4 Range analysis results

各个因素对不稳定换热系数影响的排序为岩石导热系数>当量直径>风流速度>风流温度>原岩温度，原岩温度和风流温度对不稳定换热系数的影响主要是通过改变岩石和风流传热性质，当温度发生改变，岩石和风流传热性质改变较小，所以对不稳定换热系数的值也影响较小，故可以视作次要因素考虑。

3.2 模型建立及验证

通过SPSS多元非线性回归分析，探究不稳定换热系数与各因素之间的关系。由极差分析可知，风流温度和原岩温度与不稳定换热系数不存在强相关性，所以忽略，不参与模型建立。由单因素实验可知，不稳定换热系数与风流速度、岩石导热系数、巷道当量直径和通风总体积4个因素分别呈幂函数关系，所以建立关系式，如式(11)所示：

Kτ=va·λb·Dc·Vd

(11)

式中：v为风流速度，m/s；λ为岩石导热系数，W/(m·K)；D为当量直径，m；V为通风总体积，107m3；Kτ为不稳定换热系数，W/(m2·K)；a，b，c，d为系数。

通过SPSS的非线性拟合可以得出a，b，c，d各个系数的值，如表5所示。

表5 回归系数Table 5 Regression coefficients

注：各变量对应的系数为常数，无单位。

由表5可以得到拟合关系式，如式(12)所示：

Kτ=v0.293·λ0.586·D0.013·V-0.259

(12)

该拟合关系式的R2为0.96，说明该关系式的拟合程度较高。

通过现场实测得到的数据进行模型验证，利用实测基础数据求解不稳定换热系数的计算值，不稳定换热系数的计算结果为1.09 W/(m2·K)。由式(10)对不稳定换热系数进行预测计算，不稳定换热系数的计算结果为1.22 W/(m2·K)，误差为11.1%，计算结果吻合度较高，证明该计算模型可靠。

4 结论

1)高温高湿巷道不稳定换热系数随通风时间的变化规律与普通巷道一致，均随时间的增加而降低，但高温高湿巷道不稳定换热系数高于普通巷道，当通风时间为1 a时，不稳定换热系数较普通巷道增加了12.5%。

2)通过单因素模拟实验，得到通风时间与不稳定换热系数呈负相关，风流速度、岩石导热系数和当量直径与不稳定换热系数呈正相关，风流温度和原岩温度对不稳定换热系数影响不明显。

3)利用正交模拟实验，得到高温高湿环境下各因素对不稳定换热系数的影响程度为：岩石导热系数>当量直径>风流速度>风流温度>原岩温度。

4)以不稳定换热系数为目标因子，对单因素和多因素数据进行分析，利用SPSS软件对数据进行拟合，建立高温高湿巷道下不稳定换热系数与各因素之间的计算模型，拟合程度较好，可为高温高湿巷道内热负荷计算及井下风温预测提供参考。