瓷套管避雷器的多体动力学模型与地震响应分析
苏小超,侯 磊,朱祝兵,陈予恕
(1.哈尔滨工业大学 航天学院,哈尔滨 150001;2.中国电力科学研究院有限公司,北京 102401)
避雷器是变电站中的重要电气设备之一。由于结构特征和材料属性,避雷器在地震中很容易受损,所以提高避雷器的抗震性能是提高变电站整体抗震性能的一个关键。中国电力科学研究院[1-5]使用一种铅合金减震装置来提高避雷器的抗震性能。在设备的抗震性能分析时,主要采用振动台试验和有限元仿真分析。已有研究显示了该减震装置的优秀减震效率,但目前还面临着对减震装置的优化设计问题。由于有限元仿真模型自由度高,在处理结构的非线性动力学分析、参数优化以及大变形等问题时,计算工作量大,效率不高。建立设备的低自由度简化模型对于减震装置的优化设计具有一定实用意义。
上世纪80年代末期,中国地震局的研究人员杨亚弟等[6-7]针对瓷立柱式电气设备提出质量—弹簧动力学模型,并得到一个关键的结论:对瓷套管之间的法兰连接处采用弹性处理,引入法兰连接弯曲刚度,得到的分析结果比以往采用刚性处理时更接近试验结果。该结论也被引进到GB 50260—2013《电力设施抗震设计规范》[8]中,该规范指定了计算瓷套管与法兰连接处弯曲刚度的公式。近期在立柱式电气设备的低自由度模型建立方面,有学者[9-10]针对支架—设备耦合体系,建立了2单元4自由度(2E-4D)的简化模型。该模型形式简单,计算方便,有利于进行地震响应分析和参数优化分析。但是,该方法把设备的主体看作一个单元,忽略了法兰连接处的弯曲特性。针对瓷立柱式电气设备,杜永峰等[11-12]提出了一种求解系统地震响应的半解析方法:把电气设备中的每节瓷瓶用具有分布参数的梁模拟,瓷瓶与瓷瓶的法兰连接作为柔性节点,设备顶部金属夹具等装置作为集中质量,得到具有集中分布参数和柔性节点的多节梁模型。但是得到的系统运动方程表达式比较复杂,推导过程也比较繁琐。
近年来,多体系统动力学在结构工程领域取得了很大的发展,并展示了广阔的应用前景[13-15]。与有限元模型相比,多体模型的单元之间不必满足变形连续性条件,对结构单元的变形和运动没有限制,因此在处理大变形等问题时具有一定的优势。
为建立易于理论分析且满足一定工程精度要求的数值模型,本文将利用多体动力学理论,提出一种新的建立避雷器模型的方法:把每节瓷瓶看作刚体单元,法兰连接用铰链模拟,系统的弹性用铰接点处的回转弹簧刻画,建立避雷器的多体模型。本文首先定量分析瓷套管与法兰连接处的弯曲特性,以此作为建立多刚体模型合理性的依据。其次,建立特高压瓷套管避雷器的多刚体—铰链—回转弹簧模型,并利用铰接点坐标法给出系统在地震动激励下的运动方程。最后,以1 000 kV某型号避雷器为算例进行实例分析,对比理论结果与试验结果来显示该方法的合理性和应用意义。本文所提出的建模方法形式简单,相比GB 50260—2013《电力设施抗震设计规范》[8]推荐的质量—弹簧模型,多体模型自由度更小,每节瓷瓶只需一个自由度。系统的运动方程的构建高度程式化,易于推导。
1 多刚体—铰链—回转弹簧模型
1.1 法兰连接处抗弯刚度特性
特高压瓷套管避雷器主体一般由多节瓷瓶通过法兰连接组成,结构示意图如图1(a)所示,每节瓷瓶由上、下法兰、瓷套管和内部器件构成。按照现行GB 50260—2013《电力设施抗震设计规范》[8]推荐,建立设备的有限元模型时,需要对瓷套管与法兰连接处进行等效梁处理。按此方法,瓷套管的抗弯刚度采用下列等环形截面梁的抗弯刚度计算:
(1)
式中:E为瓷套管弹性模量,D为瓷套管外径,d为瓷套管内径。
GB 50260—2013《电力设施抗震设计规范》[8]中给出了法兰连接处等效梁单元的二次截面矩的计算公式:
(2)
式中:Ic为等效梁的二次截面矩;Lc为等效梁单元的长度,取为瓷套管长度的1/20;Ec为等效梁的弹性模量;取与瓷套管相同的弹性模量;Kc为瓷套管与法兰连接处的弯曲刚度。这样,瓷套管的抗弯刚度与等效梁单元的抗弯刚度之比可用下式表示:
(3)
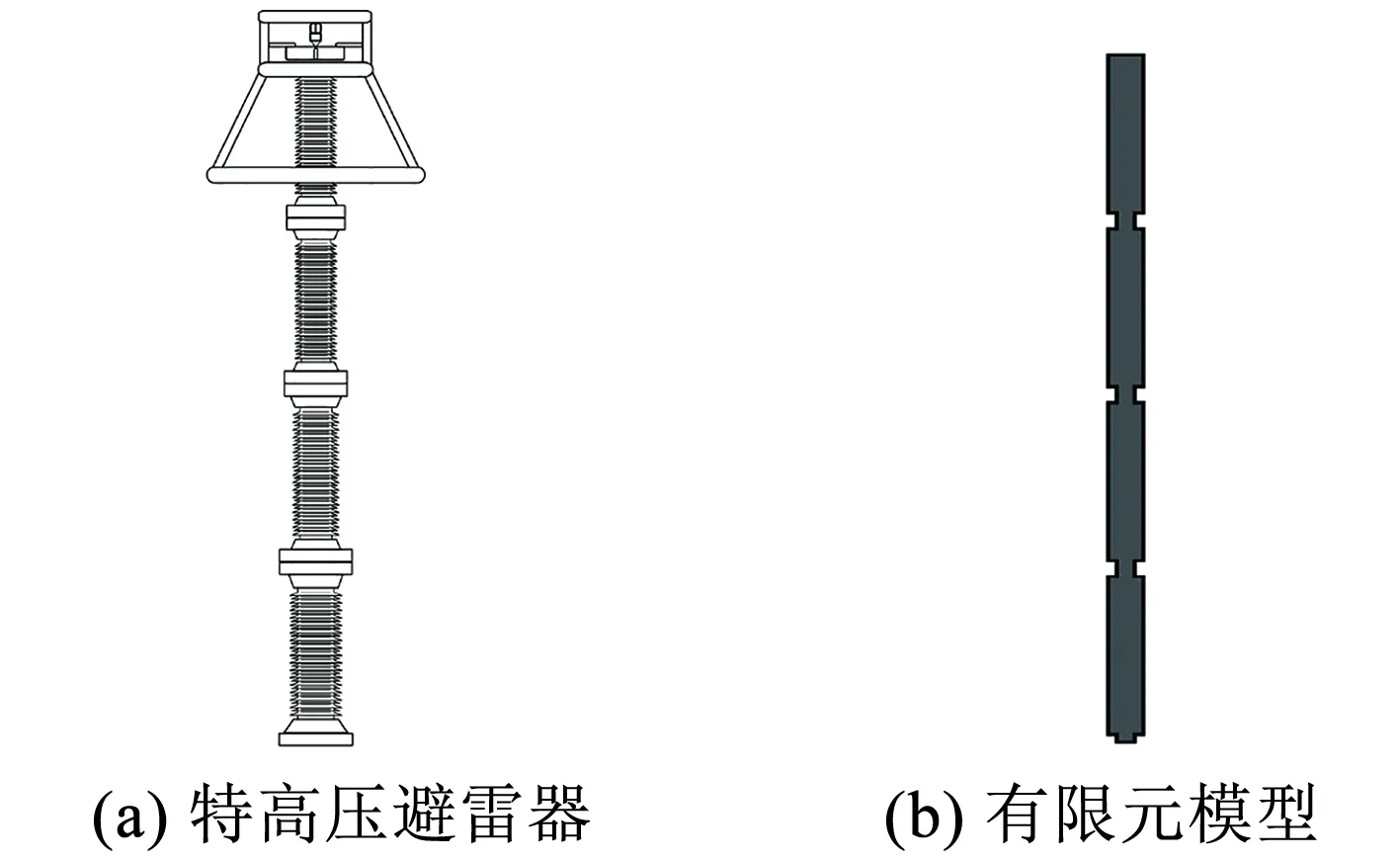
图1 特高压避雷器结构及其有限元模型示意
根据9种不同规格瓷瓶的数据,具体见表1,取陶瓷弹性模量E=110 GPa,根据式(1)~(3)计算瓷套管抗弯刚度、瓷套管与法兰连接处的等效梁的抗弯刚度以及二者之比,结果列于表2。由此可以看出,瓷套管抗弯刚度约为法兰连接处等效梁抗弯刚度的7~11倍,这定量地反映了抗弯刚度沿着避雷器的轴向分布很不均匀。按GB 50260—2013《电力设施抗震设计规范》[8]推荐得到的有限元模型如图1(b)所示,由此可知,考虑了法兰连接处弯曲刚度的避雷器有限元模型是一个变截面连续梁模型。
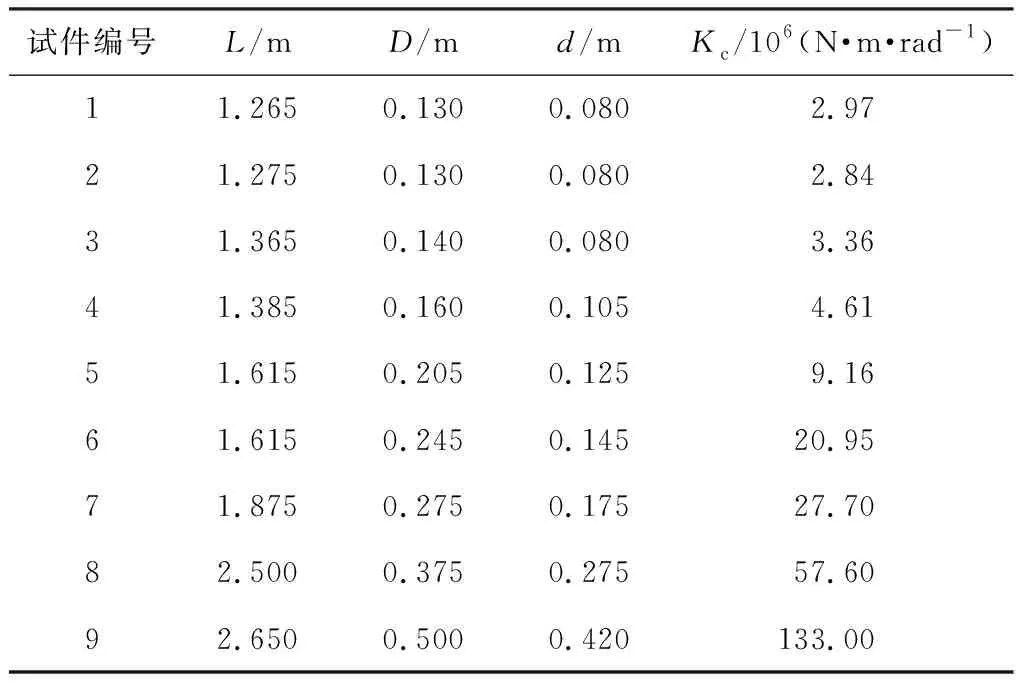
表1 瓷瓶试件的参数
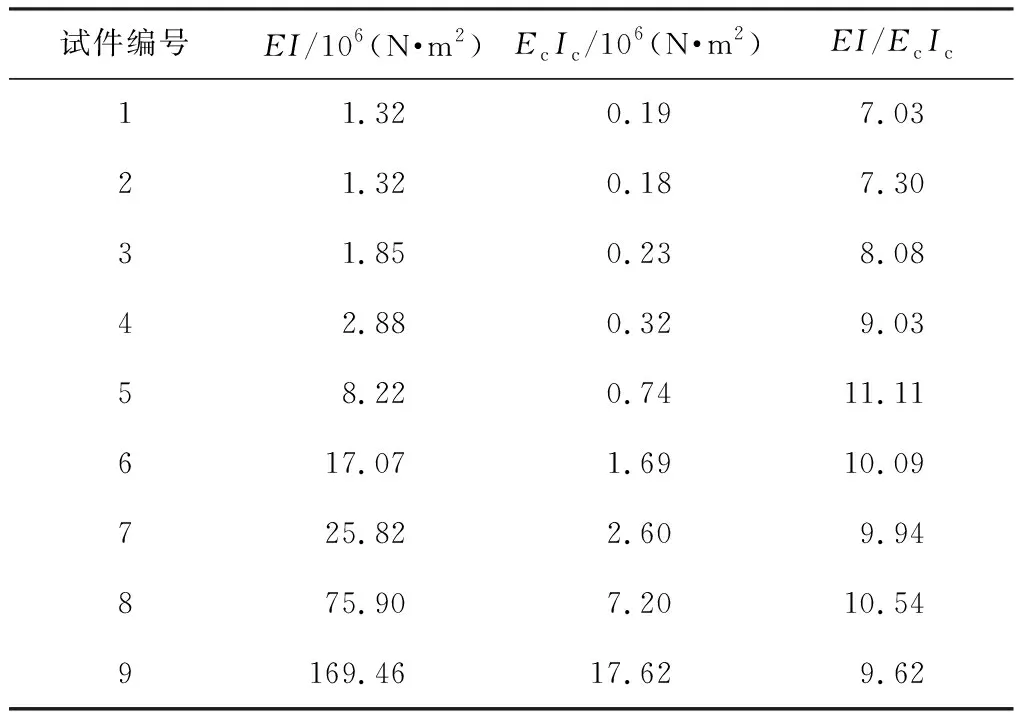
表2 E=110 GPa时抗弯刚度对比
1.2 瓷套管与法兰连接处弯曲刚度计算经验公式
在法兰连接处抗弯刚度特性中,瓷套管与法兰连接处的弯曲刚度Kc的取值由实验测得,它还可以由GB 50260—2013《电力设施抗震设计规范》[8]中给出的经验公式计算得到。该经验公式如下:
(4)
式中:β为弯曲刚度计算系数,dc为胶装部位瓷套管的外径,hc为胶装高度,te为胶装间隙。
对于弯曲刚度计算系数,在dc、hc和te的单位均取为m,Kc的单位取为N·m·rad-1的情况下,GB 50260—2013《电力设施抗震设计规范》[8]给定β=6.54×107。但是,该系数是早期基于低电压等级瓷套管类电气设备分析得到,对现阶段高电压等级的、瓷套管外径很大的电气设备,该系数取值不再适用。中国电力科学研究院[16-18]针对特高压电气设备的瓷套管与法兰连接处的弯曲刚度进行了试验研究,提出了新的弯曲刚度计算系数计算公式。新的弯曲刚度计算系数β根据胶装部位瓷套管外径尺寸dc(单位为m)取不同的数值,表达式如下[17]:
(5)
在后续分析中,将采用系数公式(5)和式(4)计算瓷套管与法兰胶装连接处的弯曲刚度。
1.3 多刚体—铰链—回转弹簧模型描述
上述分析表明,抗弯刚度的分布在法兰连接处会降低一个数量级左右,这可以启发本文对避雷器的分布弹性进行离散,把每节瓷瓶看作一个刚体,而将弹性集中到容易变形的法兰与瓷套管连接处。本文以如图1(a)所示的主体由4节瓷瓶组成的特高压避雷器为例建立设备的模型。
由于设备的对称性,可以用平面系统模拟设备。把每节瓷瓶看作一个质量分布均匀的平面刚性杆件,用回转弹簧模拟瓷套管与法兰胶装连接处的弹性,构成如图2(a)所示的上、下两端分别连接回转弹簧的刚体单元;瓷瓶与瓷瓶的连接法兰用光滑铰链模拟,并把相连端的两个回转弹簧串联形成铰接点处的一个等效回转弹簧。当考虑阻尼效应时,可以在铰接点处增加阻尼元件。把避雷器顶部均压环、金属夹具等部件看作集中质量,固接在最上节瓷瓶的顶端。整体动力学模型如图2(b)所示。
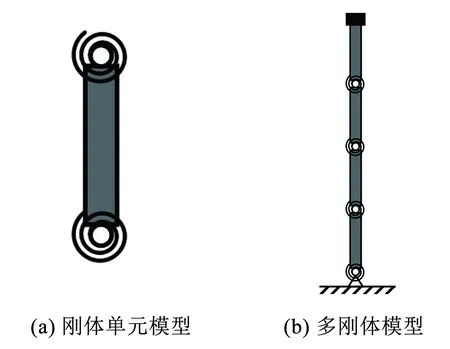
图2 避雷器瓷瓶的刚体单元模型及避雷器的多体模型
这样,本文对避雷器建立的力学模型是一个由多个刚体,并且相邻刚体之间由光滑铰链和回转弹簧连接构成的多体系统,更具体地说,是一个无杈树型开链多体系统。
1.4 动力学方程的建立
本文主要利用铰接点坐标法[19]建立该多体系统的动力学方程。主要步骤如下:
1)对系统中的刚体单元进行编号;
2)构建全局静止直角坐标参考系;
3)选取铰接点坐标θ,个数与系统自由度相等;
4)用铰接点坐标θ表示系统构型坐标向量c;
5)计算速度变换矩阵B,即c关于θ的Jacobian矩阵;
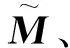
(6)
以图1(a)所示的避雷器为例,动力学方程的具体推导过程描述如下。建立如图3所示全局静坐标系,坐标原点位于初始时刻设备底部。4节瓷瓶从下往上分别编号1、2、3、4,顶部均压环对应的集中质量编号“top”。
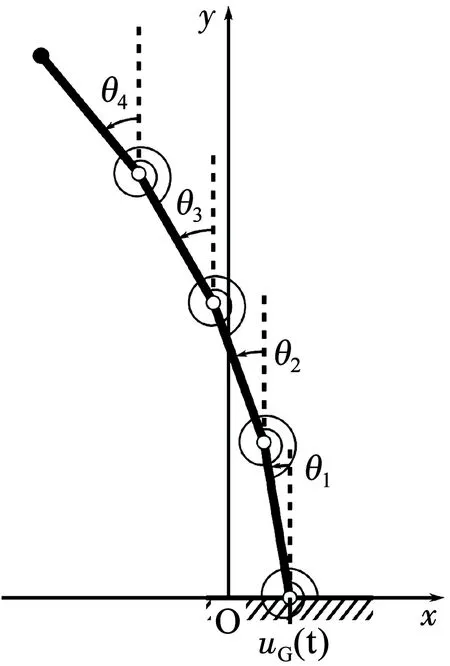
图3 多体系统模型变形示意
易知该系统具有4个自由度,选择瓷瓶单元在铰接点处的绝对偏转角θi作为铰接点坐标,记θ=(θ1,θ2,θ3,θ4)T。记单元i的质心在全局静参考系中的坐标为ci=(xi,yi,φi)T,因为质量分布均匀,刚体单元的质心与几何中心重合,设地面运动时程为uG(t),则刚体单元的全局坐标可表达为如下:
(7)
(8)
(9)
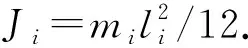
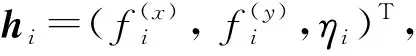
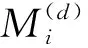
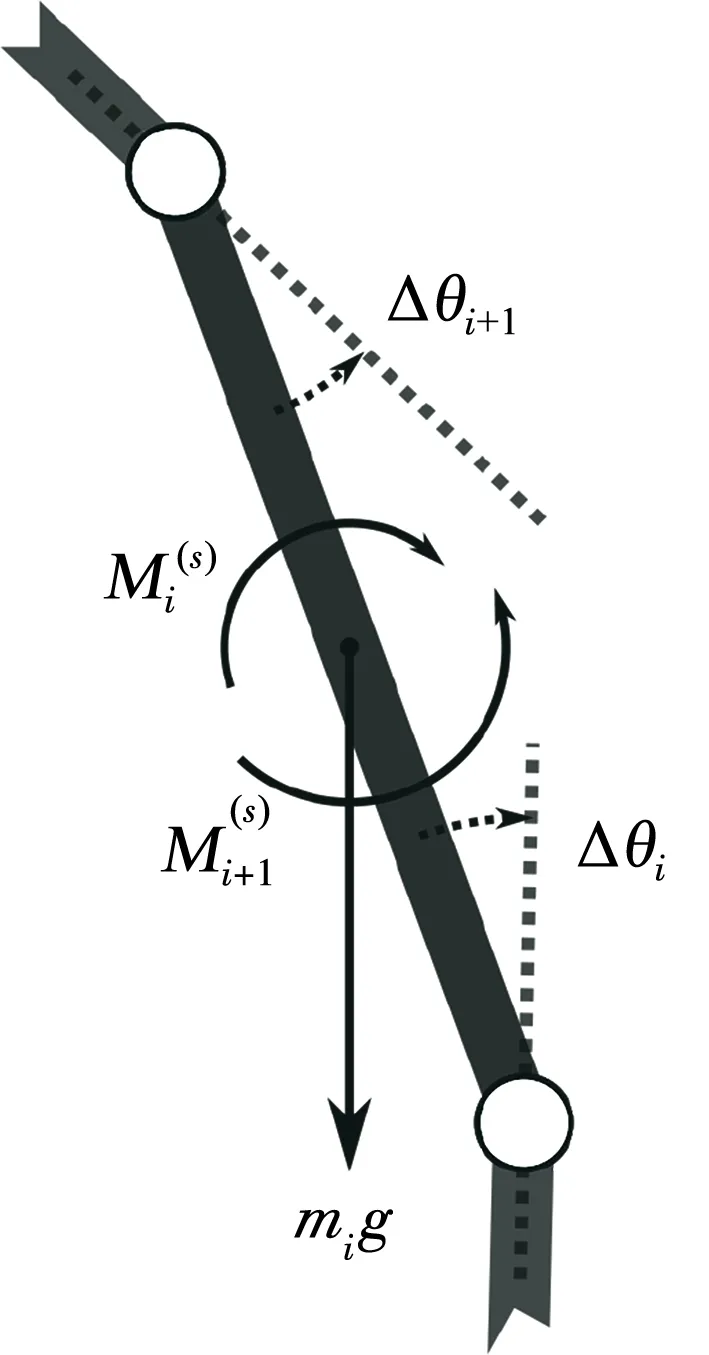
图4 刚体单元i的受力分析图
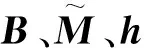
(10)
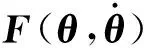
在得到系统的运动方程(10)后,从实际应用的角度,可以利用小角度假设,sinθi≈θi,cosθi≈1, 略去方程中的高阶项得到如下线性化近似系统:
(11)
其中:

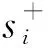
在得到系统的线性近似运动方程(11)后,可以进行地震响应时程分析,常用的数值积分方法包括中心差分法和Newmark法[20]。在进行数值求解时,除了质量参数mi,长度参数li和刚度参数si,还需要给定阻尼参数di。工程上,对阻尼分布均匀的弱阻尼结构,通常假设系统具有比例阻尼,因为本文系统在铰接点处的阻尼机理相似,分布均匀,可以采用Rayleigh阻尼假设。
通过数值积分得到每个单元的绝对偏转角θi的响应时程后,则可以利用小角度假设,按下式计算顶部相对水平位移响应时程:
(12)
用下式计算顶部绝对加速度响应时程:
(13)
用下式计算各个回转弹簧的内力矩响应时程:
(14)
在动力学方程的构建过程中进行受力分析时,在向量h相应位置加上外部载荷,去掉阻尼力作用的力矩,去掉动力平衡方程(6)中的广义速度和广义加速度项,可以得到系统的静力平衡方程:
BTh=0
(15)
该方程的展开式是关于铰接点坐标θ的非线性代数方程组。可以利用Newton法进行数值求解,进行结构静力分析。例如,分析避雷器顶端水平方向的加载与水平位移的关系。
2 地震响应分析
本文以1 000 kV某型号避雷器为算例,计算其力学特性和进行地震响应分析,并与文献[1,21]中的试验结果作对比。
该型号避雷器主体由5节相同规格的瓷瓶构成,每节瓷瓶长2 115 mm,质量为912 kg;每节瓷瓶的上、下法兰胶装参数相同:胶装高度200 mm,胶装间隙10 mm,胶装部位瓷套管外径510 mm。在试验时,基础端安装了底座瓷瓶,长623 mm,质量为300 kg,胶装高度200 mm,胶装间隙10 mm,胶装部位瓷套外径495 mm。该设备均压环及金属夹具质量为380 kg。用本文提出的方法,建立了一个6自由度平面多刚体—铰链—回转弹簧系统。
文献[21]对避雷器进行了两种工况下的抗弯试验研究:工况1最大加载力22.99 kN, 工况2最大加载力43.10 kN. 取重力加速度g=9.8 m·s-2,本文理论计算结果与试验结果对比如图5所示。
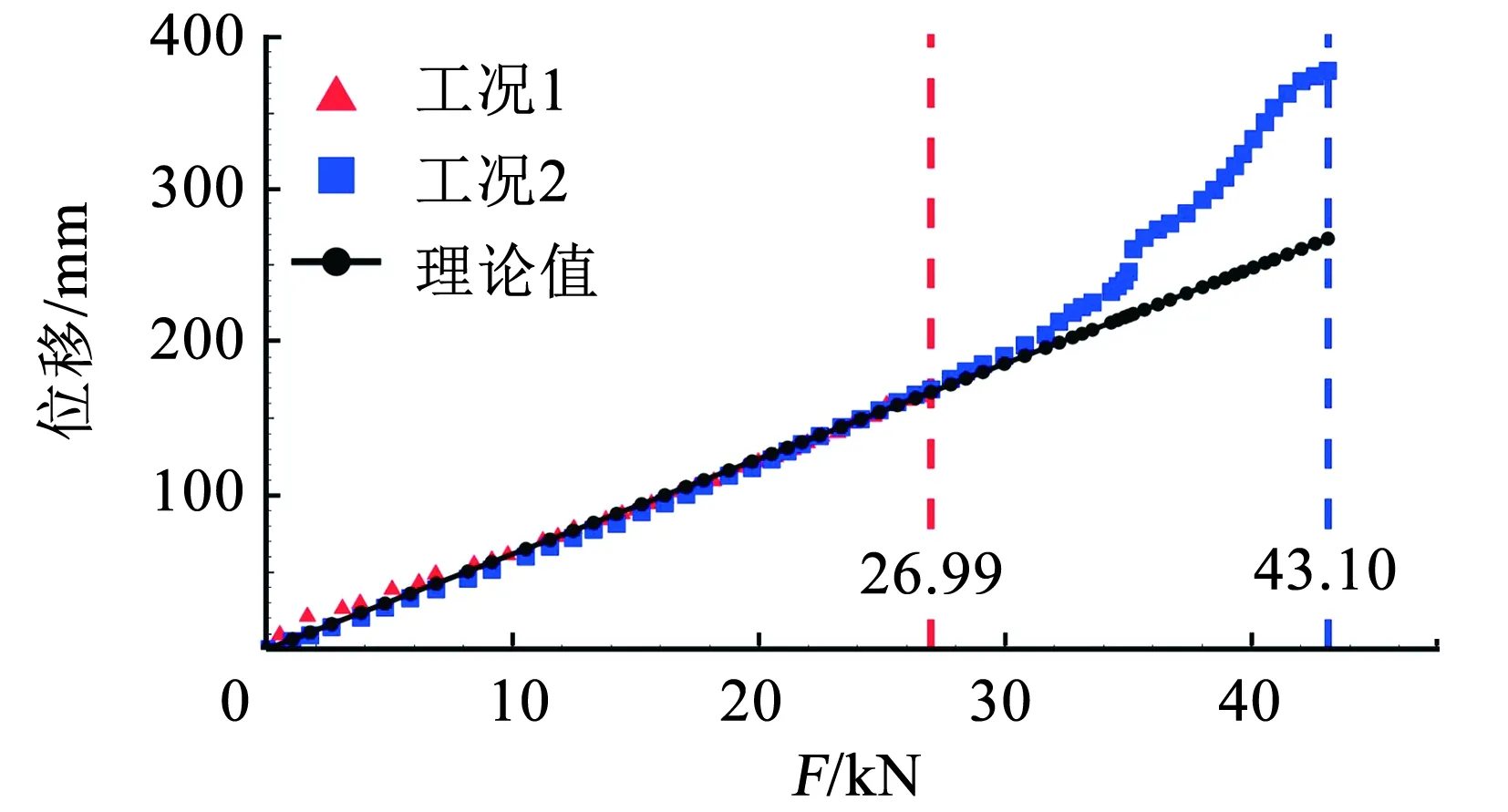
图5 试样避雷器顶部水平力与位移关系
在加载力不超过35.00 kN时,理论值与试验值误差很小。在工况1最大加载力下,理论值167.33 mm与测量值169.02 mm仅有1%相对误差。加载力超过35.00 kN后,理论值与测量值误差逐渐增大,在工况2最大加载力下理论值267.15 mm与测量值376.39 mm相对误差达到29.02%. 误差增大的原因可归结为如下:工况2进行的是破坏试验,在最大加载下,某些套管与法兰胶装连接处的变形超出了初始线弹性变形阶段,刚度有所退化;而理论计算是在假设一直处于线弹性变形阶段情况下进行的。
本文计算得到设备的基础频率为1.57 Hz,与试验值1.56 Hz对比,相对误差0.64%. 可以说理论计算结果和试验结果吻合地很好。
为了进行地震响应分析,本文利用前两阶自然频率和振型阻尼比来给定系统的Rayleigh阻尼阵。在未知电瓷设备实际阻尼比的情况下,GB 50260—2013《电力设施抗震设计规范》[8]建议阻尼比取值不超过2%. 而文献[20]指出,从小幅强迫振动试验中确定的阻尼比不应该直接应用于产生结构较大运动的地震反应分析中;在结构较小运动时确定的阻尼比并不代表结构运动的较大幅值时的阻尼。鉴于试验时,结构响应幅值较大,假设系统前两阶振型阻尼比均为3.5%。
本文计算所选择的地震动激励是0.2 g等级下中国电力科学研究院[1]试验用标准时程波。如图6所示,标准时程波地面加速度峰值1.0 g。 数值计算时,该波形乘以0.2表示抗震等级, 并乘以1.4代表支架放大系数。
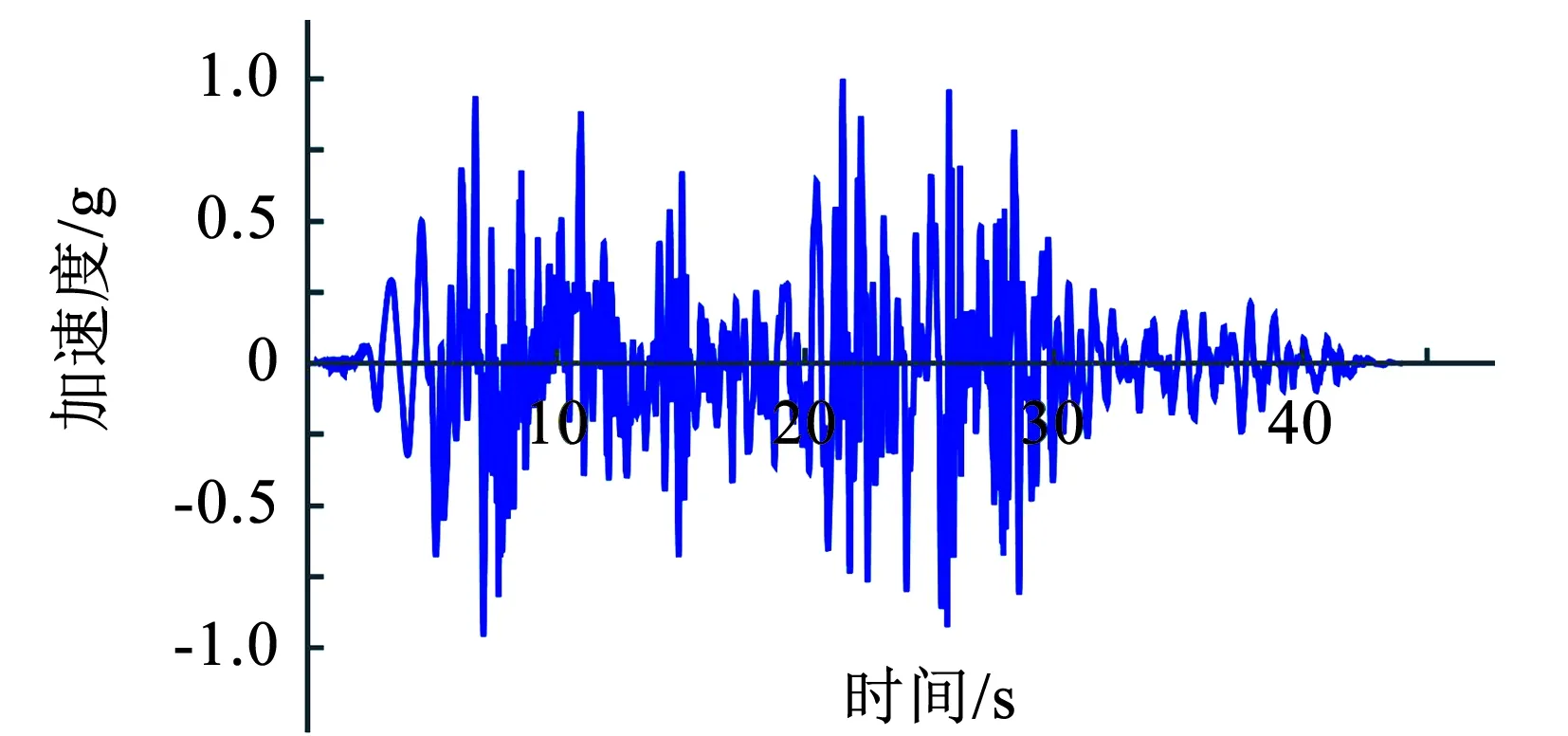
图6 标准地震动地面加速度激励
在数值求解系统各刚体单元转动角度θi的响应后,按式(12)计算顶端水平相对位移响应,结果图7所示,最大位移为104.70 mm。按式(13)计算顶端绝对加速度响应,结果如图8所示,加速度峰值为-1.08 g,与文献[1]中试验结果1.04 g误差为3.8%。
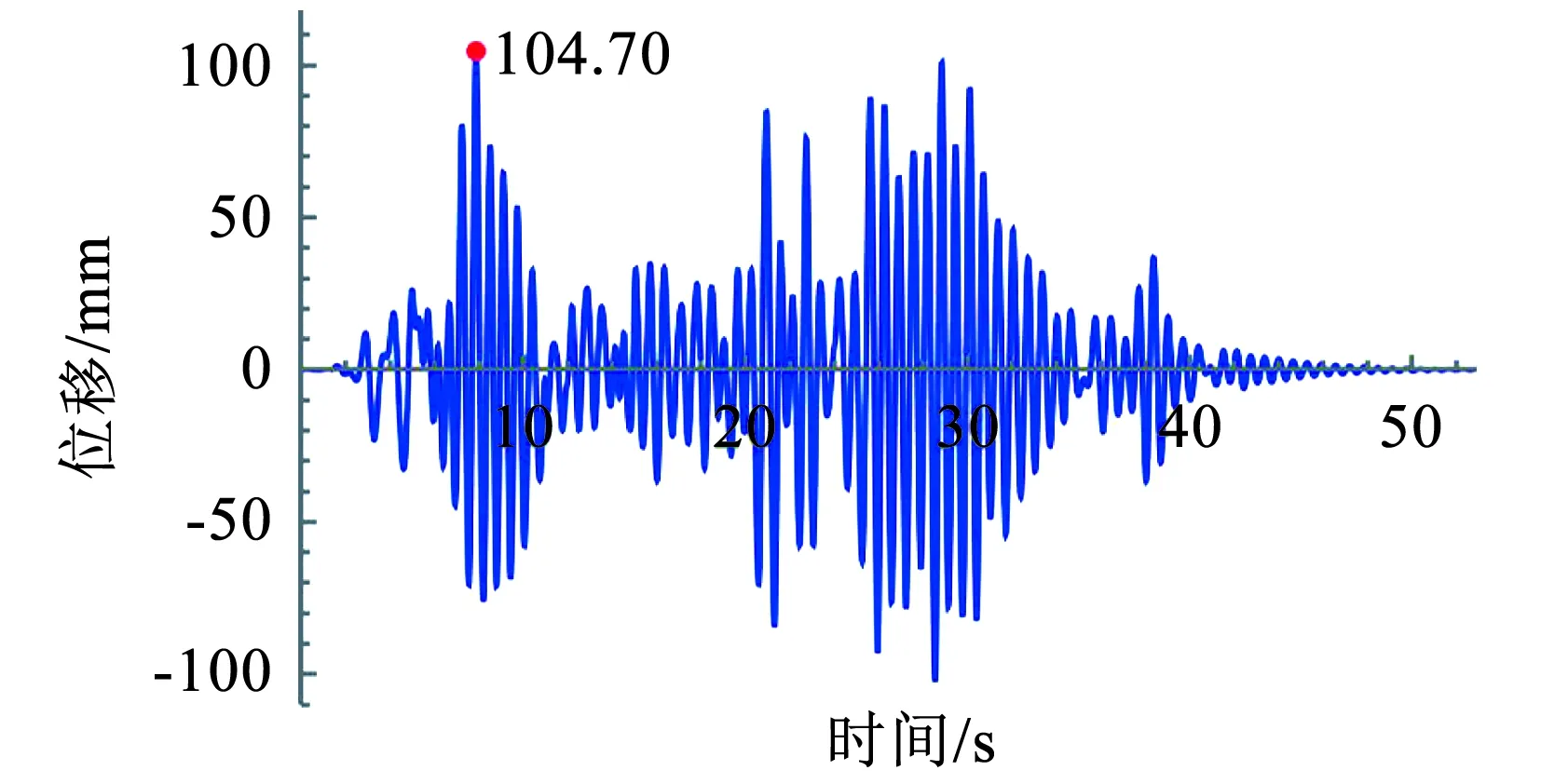
图7 顶端水平相对位移响应时程
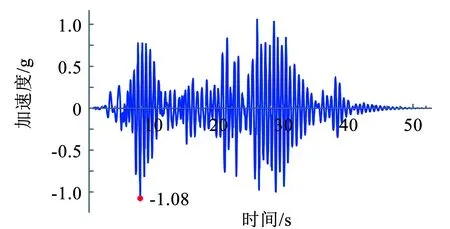
图8 顶端绝对加速度响应时程
3 结 论
1)特高压避雷器瓷套管抗弯刚度是法兰连接处等效梁单元抗弯刚度的7~11倍,表明抗弯刚度沿避雷器轴向分布很不均匀。
2)特高压避雷器的多刚体—铰链—回转弹簧模型自由度数与避雷器瓷瓶个数相等,通常不大于6,与有限元模型相比自由度数低,计算量小。多体模型的动力学方程推导过程程式化,有利于编程实现。
3)1 000 kV某型号避雷器算例的基础频率理论计算值与试验结果误差很小,仅有0.64%;顶端水平力加载与位移关系的理论结果与试验结果符合很好;地震响应时程分析加速度峰值与试验结果误差为3.8%。
4)本文所提出的建模方法形式简单,有利于进一步对加装减震装置的设备进行抗震分析和减震装置参数优化分析工作。本文虽然以避雷器为具体研究对象,但该建模方法能够方便地推广到特高压变电站中其他瓷立柱式电气设备的抗震分析中。

