基于概率模型的电子秤作弊序列码预测方法

张 娟，陈 浩

（1.西安计量技术研究院，陕西 西安 710068；2.西安理工大学，陕西 西安 710048）

0 引 言

电子秤又称为数字指示秤，是一种广泛应用于商场、批发市场和农贸市场中的计量仪器，少数商贩使用带有作弊芯片的电子秤，通过按键组合形成作弊序列码（Cheat Sequence Code，CSC），使电子秤进入作弊模式，从而实现更改重量显示，达到作弊计量的目的。这种作弊电子秤的存在，严重损害了消费者的权益。作弊电子秤的正确检测对维护市场公正具有重要的积极意义[1]。目前，针对通过作弊序列码方式激活作弊模式的电子秤，主要的检测手段是通过尝试输入预测的作弊序列码，并检查电子秤的作弊模式是否被激活来检测电子秤是否具有作弊功能。其实，作弊序列码的预测在本质上与密码破解相类似，但因其使用领域和“密码”组合类型的特殊性，使得常用的密码破解技术在该待研究问题上的效果并不显著。

对于输入的作弊序列码，目前最常用的方法是穷举法[2⁃3]，这种方法根据电子秤上数字键盘的按键数量与类型，通过排列组合的方式生成预测作弊序列码，再逐个输入电子秤进行有效性检测。这种方式的检测效率取决于作弊序列码的复杂程度和输入顺序，存在较大的偶然性，准确率与覆盖率极低。穷举法属于暴利破解，由于巨大的尝试量而导致无法在规定的时间内成功获得正确的结果。另外一种方法叫做字典法，其更贴合人类创建各种口令、密码时的规律[4]。但选择合适高效的密码字典在基于字典的密码破解中是比较困难的，再加上不同的领域或方向所设置密码的习惯不尽相同，这就使选择合适的字典难度更大。因此要想提高字典法的效率，需要根据该电子秤以及作弊序列码的特点生成专用的密码字典[5]来进行作弊码的预测。

因获取真实的大规模作弊码对研究人员来说非常困难，故本文利用机器学习领域虚拟样本生成的思想，提出了一种利用已收集到的作弊码作为小样本来生成能够高效命中待检测电子秤中作弊码的预测集的方法。在机器学习领域，虚拟样本是指在未知样本概率分布函数的情况下，利用研究领域先验知识并结合已有的训练样本，产生待研究问题的样本空间中的部分合理样本[6⁃9]。在作弊码预测集生成的问题中，先验知识表现为现有的作弊码中发现的某些作弊序列码的设置规律，作弊码预测集的目标是尽可能地生成属于真实作弊码分布空间的样本，即预测集中尽可能高效地命中作弊码。

基于这一思想，本文通过分析作弊序列码的有限样本集的结构获得作弊序列码结构模板，建立作弊序列码的概率模型，生成作弊序列码预测集，以提高作弊序列码检测集的质量和效率。

1 相关工作

由于收集到的作弊序列码有限，因此本文采用了口令生成的方法来命中电子秤的作弊序列码。目前，口令生成的方法大致分为三类：

1）基于特定场景的规则产生一定特征的口令；

2）基于字典，再结合一些变形的规则产生新的口令；

3）基于口令的概率模型，训练数据，并产生模型空间中的其他口令。

其中，基于概率模型[10⁃11]的方法相对于其他的方法具有更好的适应性和扩展性。利用概率模型生成“口令”的过程大致包括训练样本数据、建立概率模型以及再生成概率空间中可能包含的其他口令。口令模型一般又分为基于整个字符串的以及基于模板的模型。因电子秤的字符类型划分比较明确，所以本文选用基于模板的概率模型。

但该基于概率模型的方法并不能完整地描述小样本中包含的分布信息。同时，鉴于作弊码的字符组成类型较特殊，不同于常见的口令密码，对该问题的先验知识不是很明显。因此，为了保证作弊序列码检测的效率和命中率，本文在使用概率模型的基础上，结合一定的变形规则，采用基于扰动的方式[12⁃13]生成作弊序列码的预测集。

2 作弊序列码结构

目前，电子秤基于按键组合形成的作弊序列码主要由电子秤键盘上的三种字符类型组成，即数字键（D）、功能键（F）和存储键（M）。数字键主要包含键盘上的数字按键区域，取值范围为0～9。功能键主要包括“去皮”“置零”“累加”“记忆”等按键。存储键主要由多个用于存储数字的按键组成，一般表示为M1～M9。作弊序列码中，数字键的使用次数最多，其次是功能键，存储键使用频率最小。作弊序列码的组合字符不具有具体的语义信息，偏向以上述三种按键字符的随机组合，整体呈分段式，段与段之间相互独立，每个段为连续相同类型的字符。作弊序列码一般以数字键开始，功能键或者存储键结尾。

设有作弊序列码d1d2d3f1f2m1，其中d1，d2，d3为具体的数字键值，f1，f2为功能键值，m1为存储键值，其含有3 位数字键、2 位功能键和1 位存储键，对应的结构为D3F2M1，这种按顺序表示的符号结构组成方式就是其结构，也称为模板。则对于任意作弊序列码c，其模板如下：

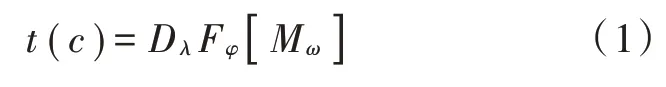
式中：λ，φ，ω分别为作弊序列码集C中三段D，F，M的长度，即数字键、功能键和存储键的数量。存储键M为可选，则c可通过模板t（c）对应的规则生成。那么对于作弊序列码样本集C，其有对应的模板集T，可由T所定义的结构生成C。若c∈C，则t（c）∈T。

电子秤作弊序列码通常为了方便记忆，其长度短，相似度高，且由于电子秤的按键数量较少，作弊序列码必须要以不影响正常的按键逻辑为前提。由于电子秤按键的特殊性，因此其可用的按键范围有限。

基于以上对作弊序列码的结构特征分析，本文通过建立作弊序列码及其模板的概率模型，基于虚拟样本生成技术设计作弊序列码变形规则，实现扩充现有作弊序列码集，生成作弊序列码预测集，提高作弊序列码检测的覆盖率和准确率。

3 作弊序列码的概率模型

为了建立有效的作弊序列码预测集，提高其在原始作弊序列码集中的覆盖率，需要生成的作弊序列码集中在概率空间的高概率部分，因此，需对生成的作弊序列码进行概率计算[14⁃18]。

作弊序列码样本集C中的元素c的概率模型表示如下：

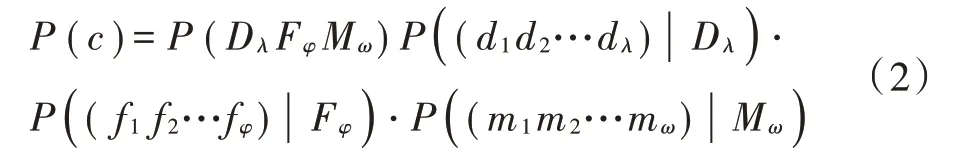
式中：d1，d2，…，dλ为具体的数字键值；f1，f2，…，fφ为功能键值；m1，m2，…，mω为存储键值；P（DλFφMω）为模板t（c）的概率；P((d1d2…dλ)|Dλ)指使用d1d2…dλ实例化Dλ的概率，即长度为λ的数字键字符串出现的频率；P((f1f2…fφ)|Fφ)指长度为φ的功能键字符串的概率；P((m1m2…mω)|Mω)指长度为ω的存储键字符串的概率。

为了进一步计算一个生成的作弊序列码的概率，这里需要计算模板t（c）以及其字符段d1d2…dλ，f1f2…fφ，m1m2…mω的分配概率。需对作弊序列码样本集C对应的模板集T进行预处理，根据字符类型分离出每个子模板t（c）对应的字符串集合片段，并为模板以及具体的字符串片段分配概率。

对于模板集T的任意模板t（c），其根据数字、功能、存储键字符类型可划分为字符段Dλ，Fφ和Mω，则有模板t（c）的字符段集合S（c），Dλ，Fφ和Mω∈S（c）。那么可得模板集T中的所有模板的字符段S1，S2，…Sn，n∈R组成了集合STR，S1，S2，…，Sn∈STR。基于以上情况，这里给出以下定义：

定义1：模板t所对应的作弊序列码的数量与模板集T中所有模板对应的作弊序列码数量之比，称为模板t的概率。

定义2：字符段s在字符段集合Si中的数量与Si的所有字符段数量之比，称为字符段s的概率，其中s∈Si，1≤i≤n，Si∈STR。

令计数函数为count，概率由函数p给出，根据定义1 和定义2 可知，集合T和Si满足：

那么，模板t以及字符串s的概率为：

式中：p（t）表示模板t的概率；count（t）代表t所对应的作弊序列码的数量；count（T）代表T所对应的作弊序列码的数量；p（s）为字符串s的概率；count（s）为s在字符段集合Si中的数量；count（Si）为Si所有字符段数量。

4 作弊序列码预测集的生成

为了对电子秤的作弊序列码进行预测，本文基于作弊序列码样本集C，结合作弊序列码的概率模型p，通过作弊序列码的模板集对样本空间进行扩充，获得虚拟样本，即作弊序列码预测集SIM，以提高对未知电子秤作弊序列码预测的准确性。作弊序列码预测集的生成过程如图1所示。

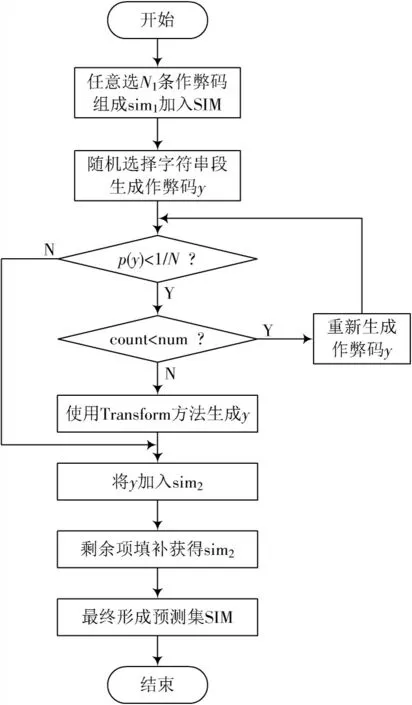
图1 作弊序列码预测集的生成流程

设作弊序列码预测集SIM 容量为N，其基于作弊序列码样本集C的模板集T生成，样本集C容量为U，模板集T的元素个数为k，k≤U。令，X为根据样本集C的每一个元素生成的预测作弊序列码个数。

根据预测作弊序列码生成的三种情况，有以下生成过程：

1）将作弊序列码样本集中的作弊序列码c1，c2，…，cu∈C形成作弊序列码预测集合sim1，加入预测集SIM，令c1，c2，…，cu∈SIM，生成的作弊序列码数量为N1=u。

2）遍历作弊序列码样本集C的元素c，获得其对应的t（c）∈T，在字符段集合STR 中搜索集合其对应的字符段集合S1，S2，…，Si，其中1≤i≤n，根据t（c）的模板结构，分别在D，F，M类型的片段所属的字符段子集随机选择字符串段Dα，Fβ，Mγ，其中1≤α，β，γ≤n），Dα，Fβ，Mγ∈S组成作弊序列码y，同时计算概率p（y），若p（y）<1N，则重新选择字符段生成作弊序列码y。若生成的y的概率p（y）<1N的次数count 大于阈值num，则基于字符段的变形规则Transform 方法重新生成y，最终获得预测作弊序列码集合sim2，sim2⊂SIM。重复此过程X-1 次，获得生成作弊序列码数量为N2=（X-1）u。

3）由于N不一定是U的整数倍，因此，需对剩余数量的预测作弊序列码进行填补，其数量为N3=N-X·u。在作弊序列码样本集C中随机选择X1条样本形成样本集，其中X1=N3X，继续使用过程2）中的方法生成作弊序列码，获得集合sim3，sim3⊂SIM。最终得到完整的作弊序列码预测集SIM。

经过以上方法获得作弊序列码预测集SIM，可对具有作弊性的电子秤进行作弊码检测，快速判断电子秤的作弊性。

5 Transform 方法

Transform 方法主要是基于以下规则对作弊序列码集C进行变形得到预测作弊序列码集合Y，从而完成SIM 的构造。不同的变形规则对结果会造成不同影响[19⁃20]，本文对作弊序列码C的变形规则定义为删除、插入、交换三种操作，之后得到Y，再将其加入SIM。下面将详细描述三类变形规则。

5.1 规则1：删除

删除规则主要针对作弊序列码中的存储键、重复字段和重复字符进行删除操作。

1）删除存储键字段。对于作弊序列码c，若其模板t（c）中有存储键（M）字段，则将整段存储键（M）字段删除。即若作弊序列码c=d1d2d3f1f2m1，其模板t（c）=D3F2M1，删除存储m1后得到作弊预测码y=d1d2d3f1f2。

2）删除重复字符。对于作弊序列码c，若其存在重复字符，则删除其中重复出现的字符。即若作弊序列码c=d1d2d1d1f1f2，模板t（c）=D4F2，删除其中重复出现的d1字符，删除后得到y=d1d2f1f2。

3）删除重复字段。对于作弊序列码c，若其存在重复字段，则删除其中重复出现的字段。即若作弊序列码c=d1d2d3f1f2d1d2d3，模板t（c）=D3F2D3，删除其中重复出现的D3字段，删除后得到y=d1d2d3f1f2。

5.2 规则2：插入

根据对作弊序列码样本集C的结构可知，数字键（D）的使用率较高，且多数集中在1～5 位。因此，该规则选择在D1或D2所对应的子集Si中随机选择字符串s插入到C中数字段的头部或尾部。即若作弊序列码c的模板t（c）=DiFjMk，然后在D1或D2所对应的子集Si中随机选取字符串Dq，q>0，将其插入到数字段的头部或尾部，得到模板为t（y）=DnFjMk（n=i+k）的作弊预测码y。

5.3 规则3：交换

该规则是按照顺序依次判断满足条件，进而对作弊序列码c进行变形得到y。

1）段内随机排序。对于作弊序列码c模板t（c）=DiFjMk，i，j，k分别代表每个段的长度，若其中存在长度大于3 的段，即i≥3 或j≥3 或k≥3，则对该段的段内字符进行随机排序，排序结果由随机函数所决定，但t（c）仍保持不变。

2）字符段逆序排列。将整个作弊序列码c按照字符类型进行逆序排序，得到作弊预测码y，即段内字符逆序排列输出。即作弊序列码c=d1d2d3d4f1f2，字符段逆序排列后得到y=d4d3d2d1f2f1。

6 实验结果和分析

为了进一步验证以上方法的有效性，实验基于计量执法过程中收缴的电子秤的作弊序列码样本建立作弊序列码预测集。

通过上述方法生成的作弊序列码预测集具有较高的真实性，并保持着样本集中作弊序列码的结构分布规律。实验从作弊电子秤的作弊序列码的命中率和运行耗时两方面测试该方法的有效性。命中率（Rate）指作弊序列码预测集在原始数据集中命中的作弊码所占的比例，这体现了该算法生成的预测集对原始数据集的还原能力。运行耗时（Time）指针对一定规模的电子秤进行作弊序列码测试，即用基于样本生成的预测集去与电子秤进行碰撞，观察能否将电子秤的作弊序列码预测成功，若能，则统计预测这些电子秤作弊码所需要的时间。

实验的主要流程如下：

1）依照作弊序列码的结构特点，随机生成规模为1 000 的原始数据集Q。按照DλFφMω的规则形式生成，1≤λ≤3，0≤φ≤1，0≤ω≤1。

2）在原始数据集Q中随机分别抽取一部分样本组成作弊序列码样本集C，样本集C的规模分别为200，250，300，350，400，450，500。基于该作弊序列码样本集C，使用本文方法生成规模为样本集C的5 倍的作弊序列码预测集SIM。

3）在原始数据集Q中剩余的样本中，依次随机选择10，15，20，25，30，35，40 条作弊序列码样本组成不同规模的测试集TS。用本次生成的预测集SIM 依次与不同规模的测试集TS 进行碰撞，统计在不同规模的TS 中的命中率（Rate）以及命中作弊序列码所需要的时间。在与某一规模TS 碰撞时，随机在SIM 中选取作弊序列预测码y去测试，选取后便不再放回。

实验的运行环境为Windows 10 系统，CPU 为Intel i7⁃8550U，内存大小为4.0 GB。

图2为样本集C的规模分别为200，250，300，350，400，450，500 情况下，测试对10，15，20，25，30，35，40 条作弊序列码的命中率情况。

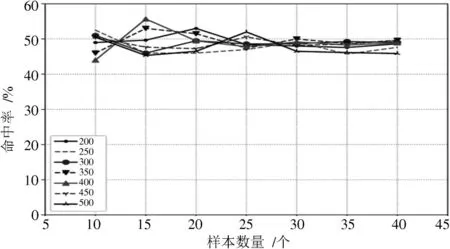
图2 不同样本规模下的命中率

由图2可知，在不同的测试集下，其命中率均在50%左右，随着测试集的增加，命中率相对稳定。可见，本文的预测方法可在不同的测试样本下保持稳定的命中率。

为了进一步说明本文方法的有效性，图3展示了预测集在对10，15，20，25，30，35，40 条作弊序列码的命中测试过程中的耗时情况。

由图3可知，在10条测试作弊序列码的耗时最短，耗时约0.025 ms；在40 条时，耗时最多，大约为0.035 ms。这表明随着测试作弊序列码的条数增加，耗时大约呈线性增加，这是由于测试过程中的对比次数相应的增多。

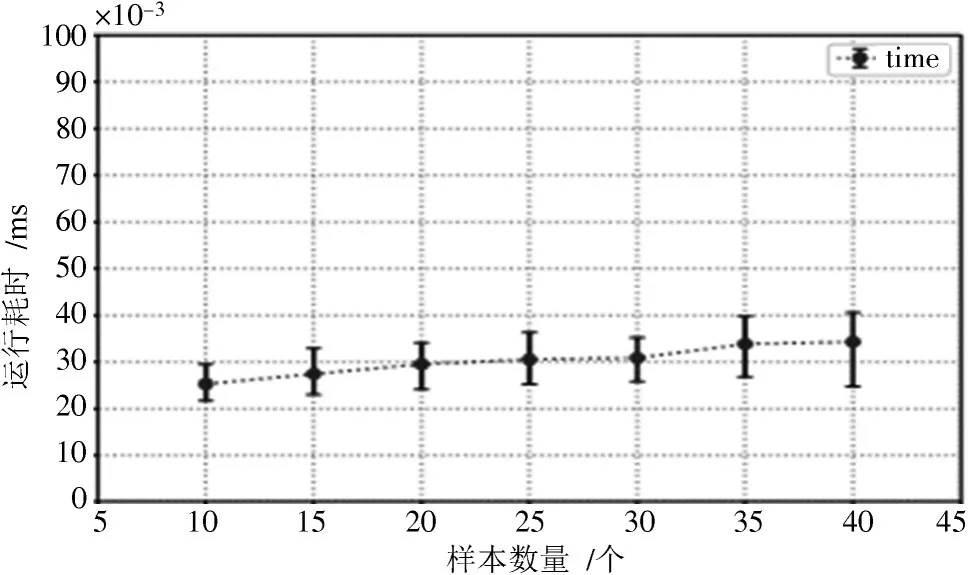
图3 不同测试样本下的运行耗时

为了能够更加直观地说明该方法的有效性，现将两种评估指标综合进行对比，如表1所示。

通过表1的数据分析可以看出，本文所提出的作弊序列码预测方法作弊序列码命中率稳定，且耗时短，表明该方法具有一定的有效性。

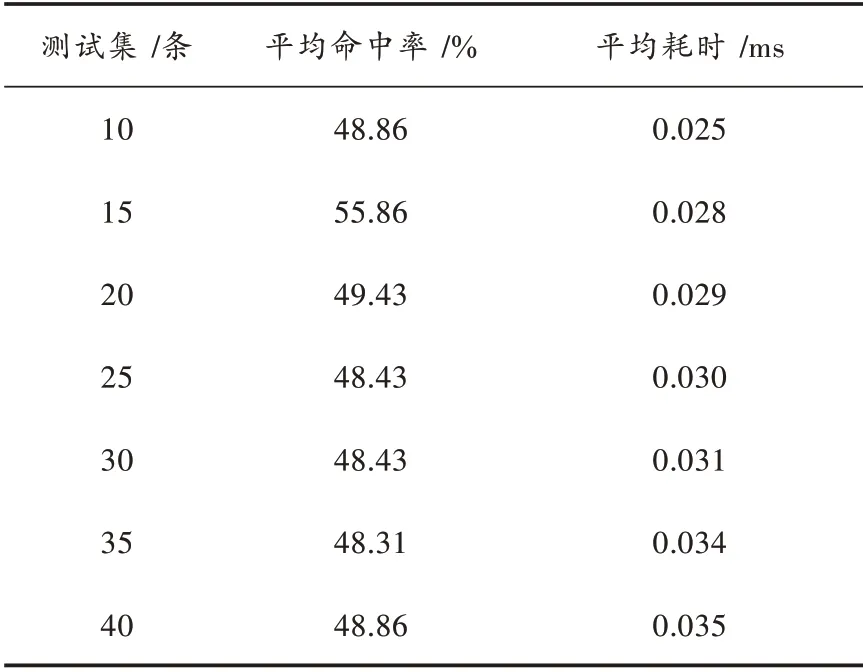
表1 不同测试样本下的平均命中率和平均耗时

7 结 论

作弊序列码的生成过程实际上是两个层次的概率组合，一层是作弊序列码的模板结构的概率组合，另一层是指示秤按键字符串的概率组合。

本文针对电子秤作弊性检测过程中的作弊序列码生成匹配问题，基于概率模型与虚拟样本技术提出一种可行且有效的电子秤作弊序列码生成方法。在接下来的研究工作中，本研究将对该方法的规则变化部分进行深入研究与优化。同时，该方法在样本空间与命中率方面还有一定的改进空间，可从作弊序列码的变形方法与扩大样本和预测集空间的比例进行进一步的详细研究，以提高电子秤作弊检测的效率。