有界格上一致模的构造

蒋玉秀, 郑 旭

(成都信息工程大学应用数学学院,四川 成都 610225)

0 引言

Yager等[1]在1996年提出了单位区间上的一致模算子。单位区间上的一致模算子作为三角模[2]与三角余模的推广和一致化,具有很多良好的性质,被广泛地应用于信息聚合、模糊系统模型、神经网络等领域[3-5],具有十分重要的理论和应用价值。

由于有界格[6]比单位区间更具一般性,因此都倾向于研究有界格上的一致模[7-21]。Karaçal等[7]第一次提出有界格上的一致模,还证明了有界格上一致模的存在性。随后,Çaylı等[12-13,15]构造了有界格上的幂等一致模。Ouyang等[16]首次引进有界格上的闭包算子(内部算子)构造一致模。Çaylı等[17-18]也给出了一些在有界格上用闭包算子(内部算子)构造一致模的方法。Ji[19]首次引进有界格上的三角次模(三角次余模)构造一致模。Hua等[20-21]也给出了一些在有界格上用三角次模(三角次余模)构造一致模的方法。一致模的构造是研究一致模需要解决的首要问题。关于一致模的构造已经有很多的结果,但是目前还没有同时基于闭包算子(内部算子)和三角次模(三角次余模)的一致模结构。本文将利用有界格上的闭包算子(内部算子)和三角次模(三角次余模)给出一致模的两种具体构造方法。

1 预备知识

定义1[6]设(L,≤)是偏序集,如果L中的任意一对元a和b,a∧b与a∨b恒存在,则称(L,≤)为格。若格(L,≤)存在最大元1和最小元0,则称(L,≤)为有界格。

文中除非特别说明,都定义L为有最大元1和最小元0的有界格。

定义2[6]设L是一个有界格,a,b∈L且a≤b。L的一个子集[a,b]被定义为

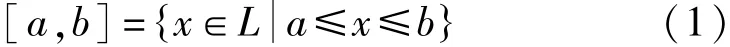
同样可以定义[a,b)= {x∈L a≤x＜b},(a,b]={x∈L a＜x≤b} 和(a,b)= {x∈L a＜x＜b}。 如果a和b无法比较大小,记为a‖b。对e∈L{0,1},定义Ie={ x ∈L x‖e}。

定理1[7]设(L,≤,0,1)是一个有界格,U是L上的一致模,其单位元e∈L{0,1},可以得到:

(1)Te=U [0,e]2:[0,e]2→[0,e]是[0,e]的一个三角模;

(2)Se=U [e,1]2:[e,1]2→[e,1]是[e,1]的一

定义3[2]设(L,≤,0,1)是一个有界格。

(1)算子T:L2→L叫作L上的三角模,如果满足交换性、结合性且对于每个变量是单调递增的,并且它有单位元1,∀x∈L都有T(x,1)=x。

(2)算子S:L2→L叫作L上的三角余模,如果满足交换性、结合性且对于每个变量是单调递增的,并且它有单位元0,∀x∈L都有S(x,0)=x。

定义4[7]设(L,≤,0,1)是一个有界格。算子U:L2→L叫作L上的一致模,如果满足交换性、结合性且对于每个变量是单调递增的,并且它有单位元e∈L,∀x∈L 都有 U(x,e)=x。个三角余模。

定义5[2]设(L,≤,0,1)是一个有界格。

(1)算子F:L2→L叫作L上的三角次模,如果满足交换性、结合性且对于每个变量是单调递增的,并且∀x,y∈L 都有 F(x,y)≤x∧y。

(2)算子R:L2→L叫作L上的三角次余模,如果满足交换性、结合性且对于每个变量是单调递增的,并且∀x,y∈L 都有 R(x,y)≥x∨y。

定义6[22]设(L,≤,0,1)是一个有界格。

(1)映射cl:L→L叫作闭包算子,如果∀x,y∈L,都满足以下条件:

(i)x≤cl(x);

(ii)cl(x∨y)=cl(x)∨cl(y);

(iii)cl(cl(x))=cl(x)。

(2)映射int:L→L叫作内部算子,如果∀x,y∈L,都满足以下条件:

(i)int(x)≤x;

(ii)int(x∧y)=int(x)∧int(y);

(iii)int(int(x))=int(x)。

定理2[19]设(L,≤,0,1)是一个有界格并且e∈L{0,1}。

(1)如果F是一个L上的三角次模且Se是[e,1]上的三角余模,则算子U:L×L→L是L上的一个单位元为e的一致模,其中U定义如下:

(2)如果R是一个L上的三角次余模且Te是[0,e]上的三角模,则算子U:L×L→L是L上的一个单位元为e的一致模,其中U定义如下:

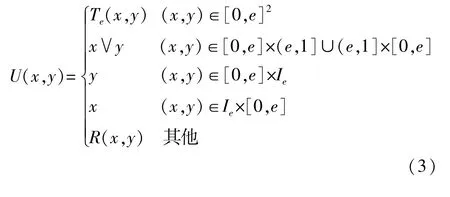
2 有界格上一致模的构造

利用闭包算子(内部算子)和三角次模(三角次余模)在有界格上给出一致模的两种具体构造方法。

定理3 设(L,≤,0,1)是一个有界格并且e∈L{0,1}。如果F是一个L上的三角次模且cl是L上的闭包算子,则算子U1:L×L→L是L上的一个单位元为e的一致模,其中U1定义如下:

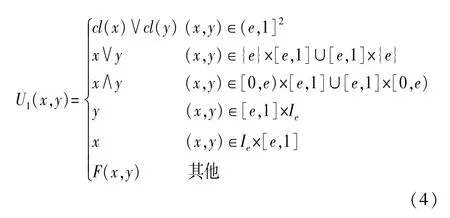
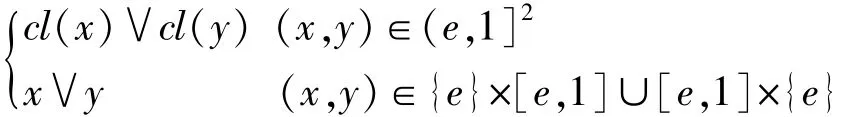
单位元:∀x∈[e,1],都有 Se(x,e)=x∨e=x。

单调性:设x≤y,∀z∈L都有Se(x,z)≤Se(y,z)。

当x=e,y=e,z=e时,Se(x,z)=e=Se(y,z);

当x=e,y=e,z∈(e,1]时,Se(x,z)=z=Se(y,z);

当 x=e,y∈(e,1],z=e时,Se(x,z)=e＜y=Se(y,z);

当 x=e,y∈(e,1],z=e时,Se(x,z)=z≤cl(y)∨cl(z)=Se(y,z);

当 x∈(e,1],y∈(e,1],z=e时,Se(x,z)=x≤y=Se(y,z);

当 x∈(e,1],y∈(e,1],z∈(e,1]时,Se(x,z)=cl(x)∨cl(z)≤cl(y)∨cl(z)=Se(y,z)。

结合性:当x,y,z∈[e,1]三者至少有一个取e时,必有Se(x,Se(y,z))=Se(Se(x,y),z);当x,y,z∈(e,1]时,有Se(x,Se(y,z))=cl(x)∨cl(y)∨cl(z)=Se(Se(x,y),z)。

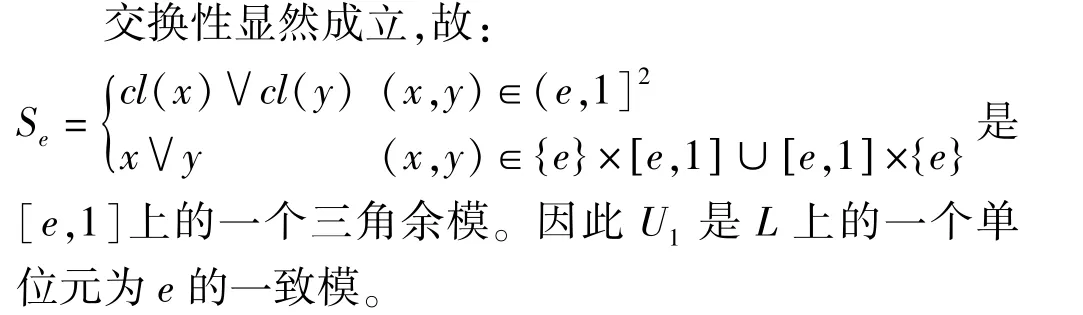
定理4 设(L,≤,0,1)是一个有界格并且e∈L{0,1}。如果R是一个L上的三角次余模且int是L上的内部算子,则算子U2:L×L→L是L上的一个单位元为e的一致模,其中U2定义如下:

证明:此证明与定理3的证明类似。

3 结束语

利用闭包算子(内部算子)和三角次模(三角次余模)在有界格上给出一致模的一个构造方法,即利用闭包算子和内部算子分别给出定理2中的三角模和三角余模的具体形式构造一致模。接下来将继续利用闭包算子(内部算子)或者三角次模(三角次余模)在有界格上构造新的一致模,以此丰富有界格上一致模的结构。