基于模糊滑模控制的双馈风力发电机阻尼控制器设计

师 磊，李现伟

(1.中国电力工程顾问集团华北电力设计院有限公司，北京 100120；2.中国大唐集团科学技术研究院有限公司中南电力试验研究院，河南 郑州 450000)

0 引言

近年来，随着风力发电装机容量不断增大，建设百万千瓦级风电场(风电基地)和实现大规模风电跨区远送成为风电发展的战略重点[1]。我国大型风电场通常分布在偏远地区，它们远离电力负荷中心，因此其输电线具有长距离和重负荷的特点[2-3]，加之风电的随机性和波动性，大规模风电并网往往会导致电力系统存在弱(负)阻尼低频振荡的风险[4]。

区域间振荡问题一直是电力系统稳定与控制研究中的一个重要课题，考虑到双馈风力发电 机 (double fed induction generator，DFIG)具有强大的功率调节能力，近年来针对DFIG抑制系统振荡进行了许多研究[5-6]。文献[7]研究了双馈风电机组并网距离，并网容量等多项因素对互联电力系统的低频振荡特性的影响，为双馈风电机组抑制系统振荡控制策略的设计奠定了基础。在以往的研究中，通过在DFIG的转子侧增加电力系统稳定器是一种比较常用且较为有效的控制方法[8-11]。文献[12]根据电力系统稳定器的设计原理，协调双馈风电机组的有功功率控制与无功功率控制，设计出了有功—无功协调阻尼控制。

随着智能算法的发展，一些先进的优化算法被运用在控制器中。文献[13]则通过运用均值方差映射算法对广域阻尼控制器的参数进一步优化。文献[14]则将人工蜂群算法与自抗扰控制思想运用于广域阻尼控制器中，显著提高了系统的稳定性。文献[15-17]将模糊控制算法运用到双馈风电机组转子侧功率控制回路中，对抑制系统振荡起到了良好效果。

以上文献表明，现阶段很多研究皆是为DFIG的功率控制环节引入电力系统稳定器(power system stabilizer，PSS)结 构 的 阻 尼 控制器对系统进行抑制，虽然这些控制器具有一定的效果但也有一定的局限性，其往往只能适用单一情况下的低频振荡效果的抑制，鲁棒性较差。针对此问题，本文运用暂态能量函数法(transient energy function，TEF)在含DFIG的两区域电力系统模型上对风电接入系统之后系统发生低频振荡的整个动态行为进行分析。基于此理论，引入模糊控制与滑模控制方法，设计出阻尼系统振荡的DFIG模糊滑模控制器(fuzzy sliding mode controller, FSMC)，在四机两区域电力系统进行模拟验证。实验结果验证了基于TEF理论的FSMC控制可以在系统低频振荡工况下起到很好的作用，证明了其鲁棒性较好。

1 基于TEF理论的振荡机理分析

TEF理论假设一个函数来描述系统在一个周期性扰动结束时的暂态能量，通过将临界能量值和计算值进行分析，估计系统的暂态稳定性，稳定性则指这两个值的差值。

通过建立含风电机组的区域电力系统探究TEF在DFIG阻尼系统振荡的机理，如图1所示。

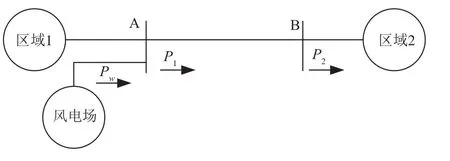
图1 含DFIG的简单电力系统模型

对图1而言，其两区域系统动态性能微分方程为：

式中： ω12与δ12为系统区域1与区域2的两个惯性中心之间的角速度转差和功角差；P1、P2表示传输线两端系统母线A、B处的有功输出；M1、M2表示电力系统区域1和区域2的惯性常数；Meq表示等值惯性时间常数；P10、P20为区域 1和区域 2 所有发电机发出的有功输出去掉线阻和负荷损耗之后的值；Pw为双馈风电场发出的有功输出；t为时间。

把零阻尼情况考虑进系统中，并且定义系统稳定时的平衡点公式为：

式中：ω120为零阻尼情况下系统稳定时的角速度转差；δ120为零阻尼情况下系统稳定时的功角差。

根据TEF原理，对系统的暂态能量函数作如下定义：

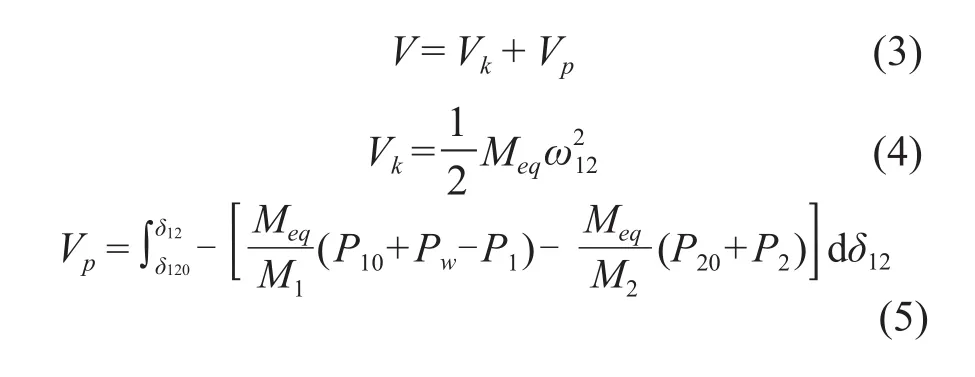
式中：V为简单电力系统暂态能量总量；Vk为系统振荡时的暂态动能；Vp为系统振荡时的暂态势能。

当系统在零阻尼状况下发生低频振荡时，系统的角速度转差ω12与功角差δ12在振荡过程中的变化特性如图2所示。在整个振荡过程中，可以根据角速度转差ω12的变化将系统的整个振荡周期分成四个阶段：阶段I，时间为t0-t1，此时，转差ω12的值逐渐由0变到最小ωmin，这就意味着系统的势能Vp降到了最小，而相应地，系统的动能Vk开始随着势能的减小而增大，逐渐达到最大值；阶段II，时间为t1-t2，此时，转差ω12的值逐渐由最小ωmin变到0，而系统的势能Vp则升到了最大，则系统的动能Vk开始随着势能的增大而减小，逐渐达到最小值；阶段III，时间为t2-t3，此时，转差ω12的值逐渐由0变到最大ωmax，而系统的势能Vp则降到了最小，系统的动能Vk开始随着势能的减小而增大，逐渐达到最大值；阶段IV，时间为t3-t4，此时，转差ω12的值逐渐由最大ωmax变到0，而系统的势能Vp开始升高到最大，相应地，系统的动能Vk开始随着势能的升高而减小，逐渐达到最小值。

图2 零阻尼状况下角速度转差ω12与δ12功角差的振荡特性曲线

根据以上四个阶段进行分析可以得知，当系统处于零阻尼状况下，系统的暂态能量总量V始终恒定不变，即系统出现低频振荡情况下，系统的动能和势能总和始终恒定。

根据式(5)可得：

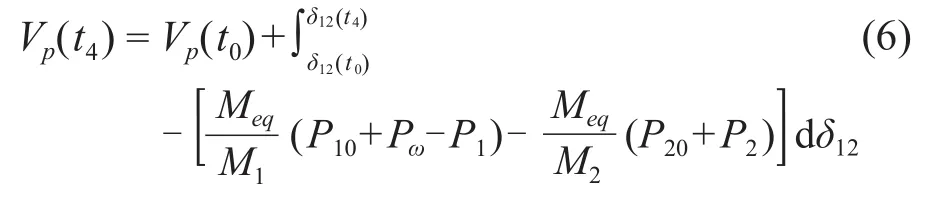
通过图2可以看出，在振荡时间为t0和t4时，系统的动能Vk(t0)和Vk(t4)的值皆是零，对于零阻尼系统而言，其势能Vp(t0)和Vp(t4)应该是个不变常数。则可得：

故此推断，自身功率可调的双馈风电场接入区域电力系统之后，如果通过双馈风电机组自身的功率调节能力来改变系统的功率输出，则会使系统的暂态能量总量V持续减小，进而保证系统的稳定性。

假定双馈风电机组的可控有功输出功率增量是ΔPw，并且其值大于零。在阶段I与II，可以通过双馈风电机组有功功率调节减小ΔPw，使该阶段的振荡暂态能量减小；在阶段III与IV，调节双馈风电机组有功输出增加ΔPw，使该阶段的系统振荡暂态能量减小=整个周期系统的振荡暂态能量减小如下：

故而，通过调节风电场的有功输出，可以改变式(5)中的积分项中的大小，进而减小系统振荡暂态能量，使系统趋于稳定。

2 基于模糊滑模控制的自适应阻尼控制器的设计

由TEF可知，可以采用同步发电机或区域之间的转子角速度偏差来判定电力系统的振荡模态。对于图1所示的两区域系统，振荡模态可以通过来进行判定，其中ω12= ω1- ω1。

由图2所示，系统振荡工况下，ω12的一个周期可分为四个阶段。在阶段I和阶段III中，ω12的幅值增加，此时增加较强的阻尼信号限制其幅值，进而导致II阶段和IV阶段ω12的振幅下降，此时增加较弱的阻尼信号，进而起到抑制系统振荡的作用。

因此，本节在DFIG转子侧变流器的有功功率控制回路中提出一个模糊滑模自适应阻尼控制器，用以改善电力系统的低频振荡，系统结构图如图3所示。

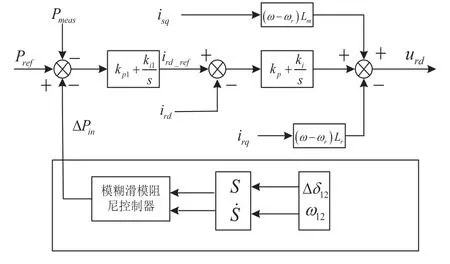
图3 含自适应阻尼控制器的转子侧变流器结构框图

由式(1)可知，区域系统的机电暂态可以通过状态变量δ12与ω12来表示，本节在设计的过程中，为了方便系统得到变量参数，δ12在这里表示区域电网母线A、B的两端电压的相角差值，而ω12则是相角差值δ12的导数。

本文设置切换函数如下所示：

其中，Δδ12= δ12-δ120，C 为切换面的权重值，并且有C＞0。

当区域电力系统没有发生低频振荡现象时，系统则有如下关系：

这时系统满足S=0，则此时的系统状态位于切换面上。

构造Lyapunov函数如下所示：

为了系统的运动点能做趋向于滑模面的运动，当运动点位于切换面附近时，需满足以下条件：

式(12)保证了在切换线S=0的任何一侧的邻域中，状态量的运动都朝向切换线。

3 算例验证

本文采用Matlab/Simulink软件搭建含风电场的区域系统模型，模型采用IEEE四机两区域系统，系统中的两区域分别包含两个额定容量为900 MW的同步机，且同步机G1～G4参数相同，接入的风电场容量为150 MW，且为了更好的分析，所有风机采用单机等值模型，具有相同的工作状态，即采用100台1.5 MW的DFIG，风电场通过10 km长的输电线接入电力系统的母线1处，如图4所示。

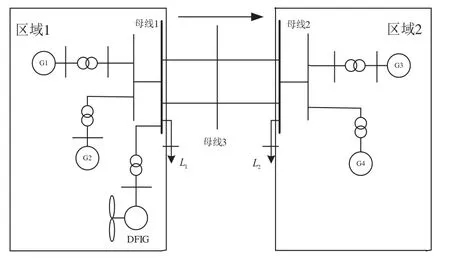
图4 风电接入的四机两区域电力系统模型

为了对比突出本文所设计控制器的有效性，借用PSS控制理论，引入控制结构进入DFIG的有功功率控制环节中，将Δω为附加控制器的输入信号，进行有功功率附加阻尼控制器设计，其系统控制框图如图5所示。

图5 附加阻尼控制框图

其中控制框图中控制器由四部分组成，主要包括增益参数、隔直环节、相位补偿模块与限幅模块。

3.1 三相短路故障分析

首先测试附加阻尼控制器在三相短路故障下抑制系统振荡的情况，在区域电力系统进行仿真实验，系统运行至15 s时，在图4中的母线3处设置一个持续时长为0.1 s的三相短路故障。通过示波器观测系统中各变化量，将模糊滑模控制与无附加控制和图5所示的PSS附加阻尼控制的情况进行对比，判断模糊滑模控制策略抑制系统低频振荡的有效性，系统中各变化量如图6～图8所示。

图6为同步机G1、G2分别相对于同步机G4的相对转子角d14和d24的试验曲线。由图所示，与无附加控制相比，考虑附加阻尼控制和FSMC控制两种工况的振荡稳定时间比无附加控制工况更快速。附加阻尼控制与FSMC控制工况相比，FSMC控制下d14和d24提前3.7 s达到稳定状态，振荡峰值也有降低。

图6 三相短路下G1、G2相对于G4的相对转子角

图7为联络线的有功功率的响应曲线。由图所示，采用FSMC控制工况下，传输线功率振荡波动较小，故障发生后振荡3 s趋于稳定，稳定时间比考虑阻尼控制工况下提前了2 s，证明了FSMC控制在抑制系统振荡情况具有较好的鲁棒性。

图7 三相短路下传输线有功功率振荡响应曲线

图8为三相短路故障工况下有功功率的响应曲线。由图所示，若无附加装置的DFIG进行响应三相短路故障工况时，DFIG有功功率在进行故障暂态响应之后无动作，系统持续较长时间振荡工况。系统发生故障时，考虑附加阻尼控制和FSMC控制情况下DFIG的有功功率控制环均参与了系统的调节，有功功率可随着振荡做出响应动作，具有抑制振荡的作用。

图8 三相短路下双馈风电机组有功功率的响应曲线

3.2 机端扰动分析

通过增加机端扰动特例进一步测试所提出的控制策略的有效性，工况如下：在图4所示的模型中，系统运行至15 s时，在同步发电机的励磁参考电压 处增加10%的阶跃扰动，使Vref的值由1.0 p.u.突降至0.9 p.u.，持续时间0.6 s，扰动去除，系统恢复正常，观察系统变量响应。

由图9～图11所示，与三相短路故障相似，当机端扰动工况下，FSMC控制可以使DFIG有功环快速做出响应动作抑制系统振荡。并且由于FSMC控制具有模糊控制和滑模控制的优点，其具有更好的控制效果。

图9 机端扰动下G1、G2相对于G4的相对转子角

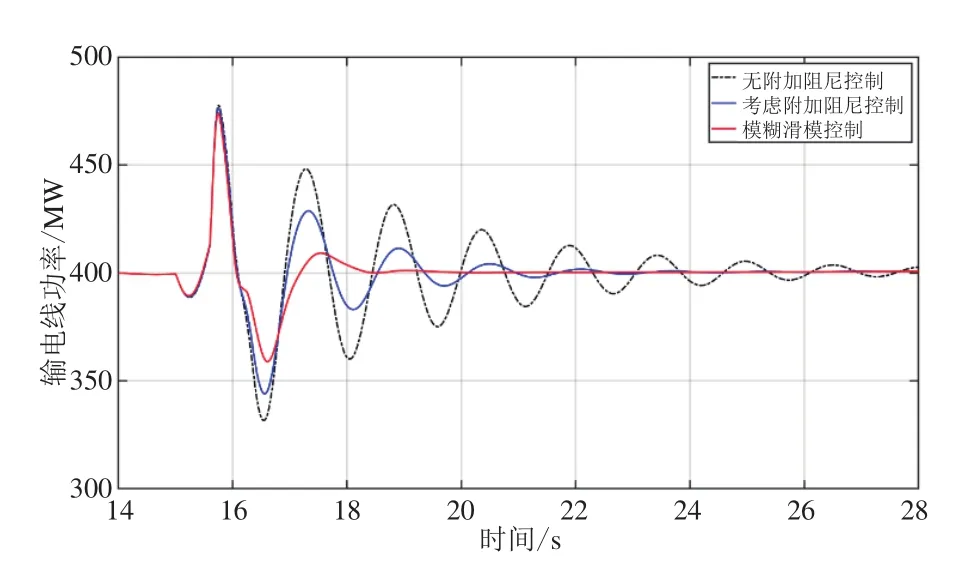
图10 机端扰动下传输线有功功率振荡响应曲线

图11 机端扰动下双馈风电机组有功功率的响应曲线

3.3 负荷突变扰动分析

本节通过设置负荷突变扰动进一步测试双馈风电机组转子侧有功控制环附加阻尼控制器的有效性。设置如下：在四机两区域模型的母线3处加装500 MW负荷模块，运行过程中通过负荷突变来模拟低频振荡环境。系统实验仿真结果如图12～图14所示。

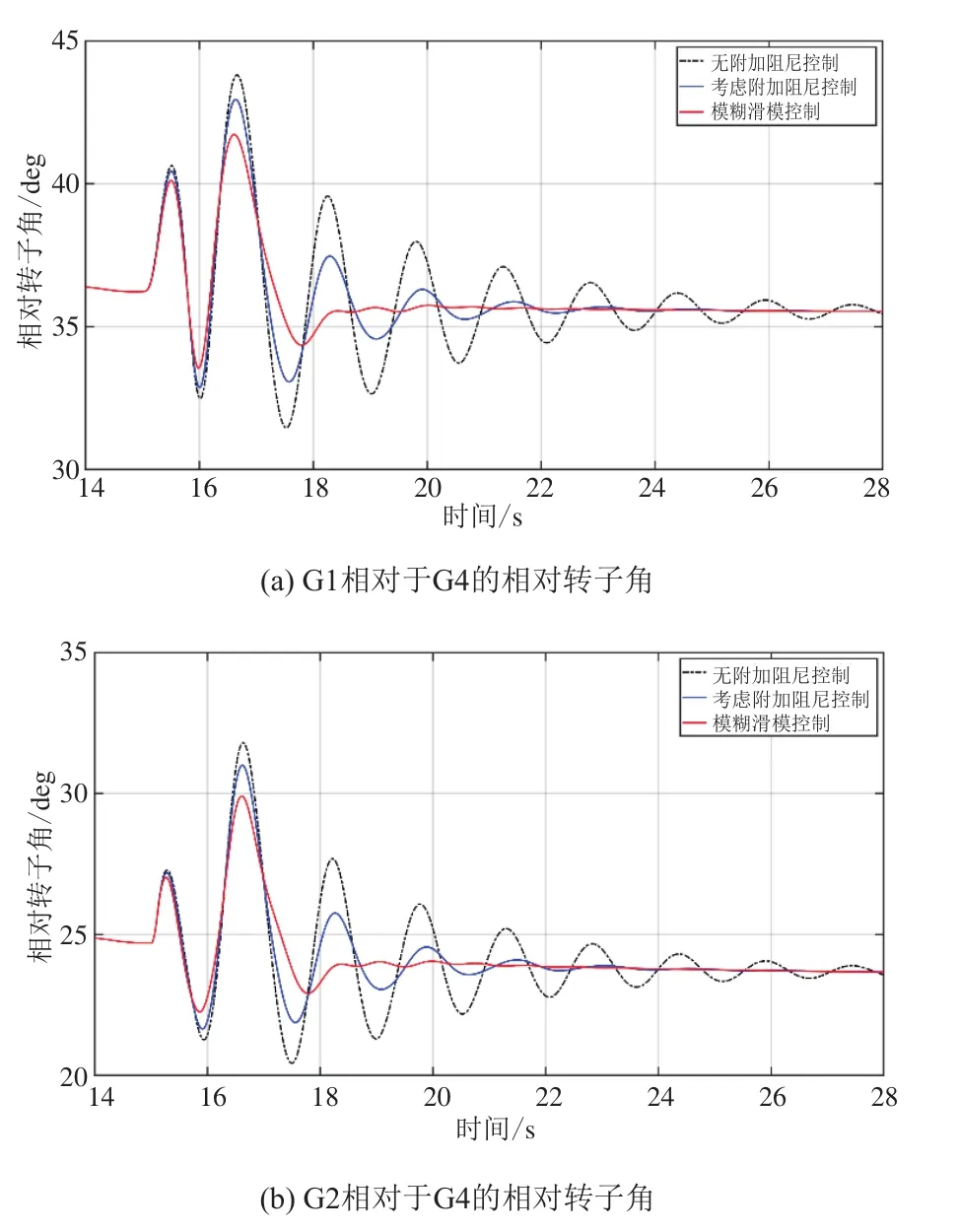
图12 负荷突变下G1、G2相对于G4的相对转子角

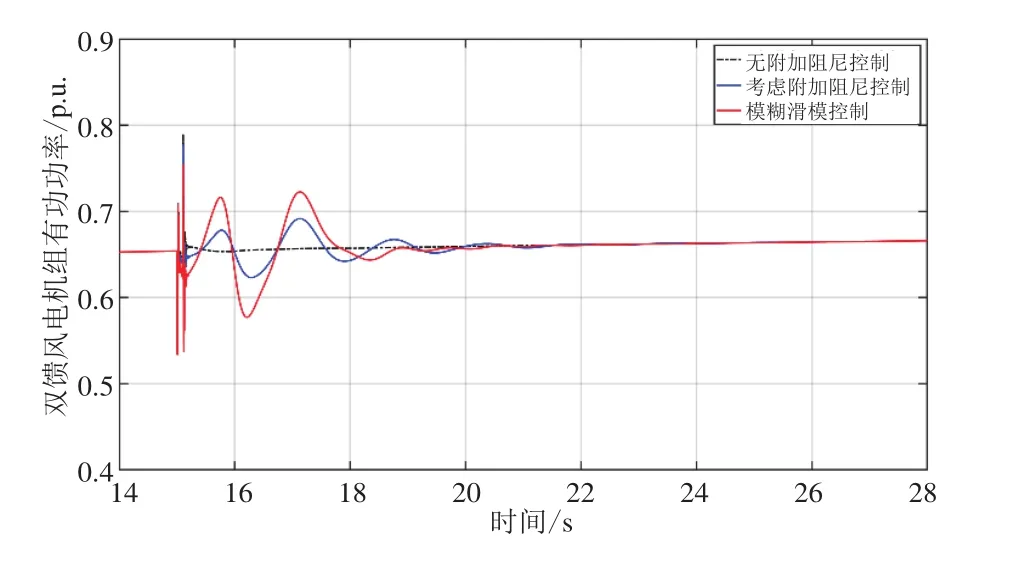
图13 负荷突变下传输线有功功率振荡响应曲线

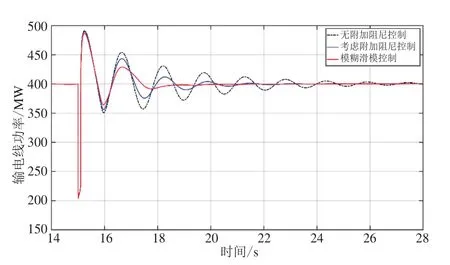
图14 负荷突变下DFIG有功功率的响应曲线

从图12～图14可以看出，负荷突变扰动工况下，采用模糊滑模控制的DFIG在变风速情况下，仍能为系统提供功率支撑，可以使振荡系统更快的趋于稳定。

4 结论

通过研究TEF基本原理，结合模糊控制与滑模控制，设计出了基于FSMC控制的DFIG阻尼控制器，并在四机两区域系统上进行了仿真验证。通过运用Matlab软件进行三相短路故障、机端扰动和负荷突变扰动三种工况的模拟验证，验证了基于FSMC控制的DFIG阻尼控制器在抑制系统振荡的有效性，由于该控制器具有模糊控制与滑模控制的优点，故而在改善含风电机组的电力系统阻尼特性方面具有较好的鲁棒性。