一种适用于窄波束雷达捕获空间目标的等仰角搜索方法

刘科君 徐 劲 曹志斌

(1中国科学院紫金山天文台 南京 210023)(2 中国科学技术大学天文与空间科学学院 合肥 230026)(3 中国科学院空间目标与碎片观测重点实验室 南京 210023)

1 引言

通常雷达观测空间目标的过程是根据点位预报的引导,捕获目标并跟踪获取数据,因此对于点位预报的精度有一定的要求,特别是影响最大的沿迹误差部分[1–2],对视场很小(例如0.1°甚至更窄)的高频窄波束雷达而言,点位预报就有可能失效.

为解决此问题,可以从提高预报精度和改变雷达工作模式两方面入手,目前已有一些针对性的积极工作[3–6],如文献[5]针对主要作用在沿迹方向却难以精确计算的大气阻力,从沿迹误差发散规律的表达式中寻求特殊条件,调节预报段的大气阻力系数,让初值和模型的误差得到“抑制”或者“抵消”,从而使得误差发散斜率趋近于0.这个方法能将短期预报精度提高45%左右.

文献[6]从改变雷达工作模式出发,提出采用低频宽波束和高频窄波束相结合进行点位搜索的方式,即先由低频宽波束根据目标指向预报的程序引导,完成对目标的捕获和跟踪,然后转同轴高频窄波束对目标继续进行捕获和跟踪;或直接使用高频窄波束,在对目标过境点位进行搜索的同时,在较小的预定区域以叠加螺旋扫描[7]搜索的方式实现目标捕获.

本文借鉴前人观测激光卫星的凝视和拦截预报思想[8–9],提出了一种适用于窄波束雷达捕获空间目标的等仰角搜索方法,该方法的基本出发点是:虽然不能确知沿迹误差,但可以先行预估沿迹误差的范围,同一轨道上沿迹误差范围内不同位置的目标,受地球自转的影响,到达测站当地某个过境仰角的时间和方位角将随目标沿迹位置的前后关系呈单调变化,因此实际目标到达这个仰角的可能时间和方位角均存在一个有序变化范围.基于这个规律,可以通过搜索指定一个合适的仰角,根据雷达的有效波束直径,在方位角范围及其相应的时间范围内进行有序分割,以生成雷达的系列引导数据,雷达按这些引导数据在指定仰角上对目标进行搜索,其效果相当于对沿迹误差范围内的目标在指定仰角上所有可能出现的位置实施遍历观测,而目标的实际位置就在其中.

2 方法步骤

等仰角搜索可以形象地描述为:雷达观测目标时,其波束指向的仰角始终保持不变,根据计算出的引导数据,按照时间的推移单向调整波束指向的方位角,从而完成对目标的搜索捕获.具体算法步骤如图1所示.

图1 等仰角搜索流程Fig.1 The procedure of constant elevation search method

详细步骤描述如下:

(1)根据空间目标(本文主要针对低轨高动态目标)的一组初始精密轨道根数σq(tq,→rq,˙→rq,ϵ)(其中tq为该组轨道参数的历元时刻,→rq、˙→rq分别为目标相对于历元地心惯性系的位置和速度矢量,ϵ为目标面质比),使用数值积分[1]方法和高精密力学模型(力模型包括地球非球形摄动、日月引力、大气阻力)[1]外推计算出某次过境中间时刻t0的位置速度矢量→r0和˙→r0,转换为第一类无奇点变量形式的初始拟平均根数[1,10],建立一种简化分析摄动模型,用于计算该次过境期间的目标根数变化.此简化分析摄动模型在目标该次过境时间段内,仅包含轨道摄动变化的一阶长期项、一阶短周期项以及二阶短周期项中由地球自转引起的少量降阶项;

(2)依据预估的沿迹误差范围,可以将t0时刻的初始拟平均根数等时间间隔离散为一系列仅平纬度角λ不同的虚拟目标,各虚拟目标对应于同一轨道上的不同沿迹位置,且时差分布恰好覆盖预估的沿迹误差范围.由于地球自转,从观测站的角度看,各虚拟目标在一次过境期间所产生的不同视轨迹将组成一个视轨迹簇,其中每条视轨迹的观测仰角都是呈先升后降变化,在近站点达到仰角最大值,并且视轨迹簇中的最大仰角具有逐步变大(接近天顶)、逐步变小(远离天顶)、先逐步增大过天顶后再逐步变小3种变化规律;

(3)雷达观测的前提是可见,同时需要获取数量足且质量高的观测数据,这就决定了近站点不可见或可探测弧段太短的视轨迹都是无效的,可据此结合雷达的观测条件(作用距离和仰角限制)进行筛除[11–12].视轨迹簇的连续变化特征使得所筛除的若干视轨迹一定集中、连续地处于视轨迹簇的两端或其中一端,因此筛除后的视轨迹簇仍然具有连续性,从而可以计算出剩余视轨迹最大可探测仰角的最小值H和最小可探测仰角的最大值h,根据视轨迹簇的连续变化特征和雷达作用距约束条件可以证明H总是大于h,于是可确定该次过境的搜索仰角取值范围:hs∈[h,H].由于过境的搜索仰角可选范围在计算前是未知的,因此无法直接指定搜索仰角,但可以通过设置一个比例因子β,使搜索仰角按下式取值:hs=h+β×(H-h);

(4)根据选取的有效搜索仰角hs,可以计算各连续虚拟目标上升到该仰角时的特征参量,包括目标到达时刻tk、方位角Ak、观测斜距ρk等,k按照沿迹位置先后依次表示不同的虚拟目标.考虑到目标运动的角速度远大于地球自转速度,则可断定各虚拟目标上升到搜索仰角hs的时间tk和方位角Ak随k的单调变化(方位角需经连续化处理).因此可认为真实目标上升到搜索仰角hs时的可能方位角与对应时间存在严格单调函数关系,虽然真实目标上升到搜索仰角hs时的方位不确知,但它如果出现在某一个方位,则只可能出现于一个唯一的时刻.这一时空关系结论使得在沿迹误差估值范围包含实际沿迹误差的前提下,雷达按时序进行等仰角搜索时能够遍历真实目标所有可能出现的方位.因此可以tk为基点,利用基点上的特征参量,采用三次自然样条内插[12]构建关于方位、斜距等的插值函数A(t)和ρ(t)等.同时,由于构造出的方位角A(t)是时刻t的严格单调函数,其存在一个唯一的逆函数,可以Ak为基点构造出插值函数t(A),用于给出真实目标在一个连续的方位角范围内可能出现的不同时刻;

(5)记步骤(4)中目标上升到指定仰角hs的时间范围对应的方位角范围为ΔA.与之相对应的,雷达在指定仰角hs上的搜索范围记为Δψ.对Δψ按照雷达有效波束直径进行均匀划分后,即成为若干个搜索子区间,每个子区间的值均为Δψ*;ΔA也相应地被划分为同样多个子区间,每个子区间的值均为ΔA*,如图2所示.将雷达波束按时间顺序依次摆放于每个Δψ*的中心方向,该方向的方位角即为对应ΔA*的中心方位角;每个Δψ*代表一次波束驻留,驻留的起止时间即为对应ΔA*的首末端点时间(可通过步骤(4)中构造的插值函数得到),这样就形成了等仰角搜索过程.实际上,由于非沿迹误差(法向和径向)未在预估误差中考虑,需要将按有效波束直径划分的子区间适当重叠,才能在非沿迹误差增长不超过有效波束半径的前提下保证搜索无遗漏,重叠示意图如图3所示,δ表示子区间的重叠比例.

图2 指定仰角上的搜索范围及子区间划分方法Fig.2 The search scope and division of subinterval on a specified elevation

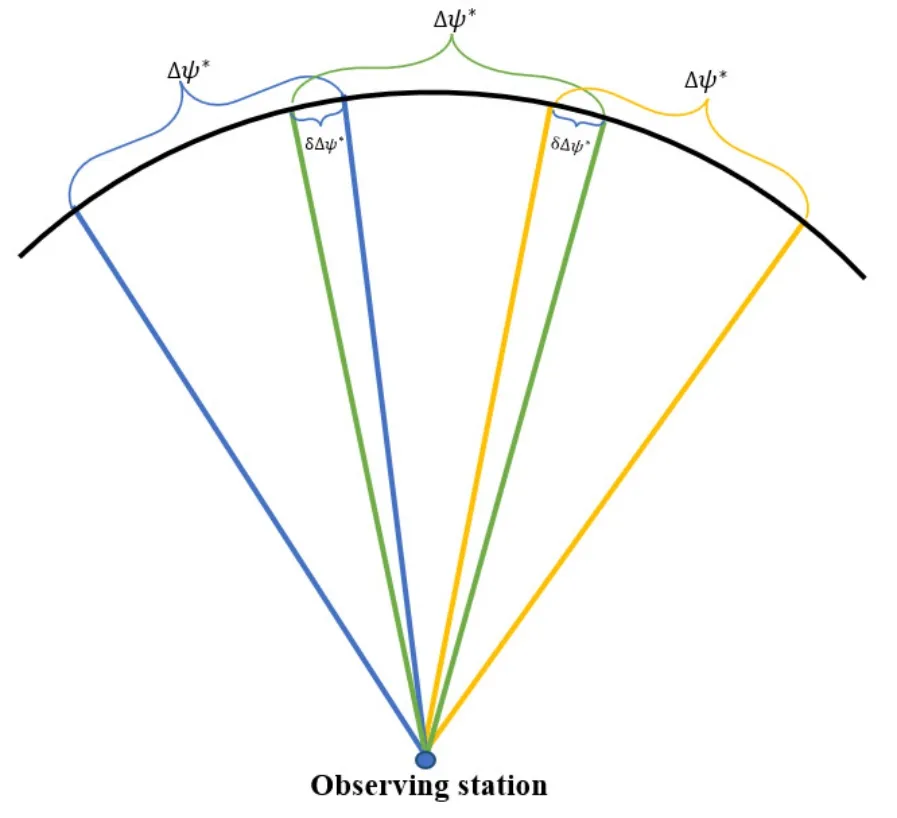
图3 子区间重叠方法Fig.3 The overlap method of subinterval

3 等仰角搜索方法的效果验证

3.1 验证方法

为了验证等仰角搜索方法是否有效,本文与采用SGP4(简化常规摄动模型)的点位预报结果进行了对比,选择激光星为测试目标,选取该目标的一个过境时段,并以若干天前的TLE(双行轨道根数)为初始根数,分别产生该过境时段的等仰角搜索数据和点位预报数据,然后使用国际激光测距服务(ILRS)发布的激光星精密星历解算的站心系观测量为比对数据,比对数据时刻取整秒点.

(1)等仰角搜索方法

从某一过境区间中选择一个有比对数据的仰角值作为搜索仰角,计算波束按该仰角搜索时的引导数据,包括若干驻留波束的起止时刻、中心指向的方位角以及驻留波束中心指向上的激光星距离.按照比对数据的历元时刻查找对应时间区间的驻留波束,比较该驻留波束中心指向与比对数据站心观测矢量的夹角,即指向偏差.若指向偏差小于波束有效半宽,则代表等仰角搜索有效,否则代表其失效.

(2)点位预报方法

采用SGP4模型预报该激光星在同一个比对数据时刻的位置和速度,进而计算其相对于测站的方位角和仰角.比较预报点位的站心观测矢量与比对数据的站心观测矢量的夹角,即点位预报的指向偏差,比较依据同上.

3.2 算例分析

3.2.1 有效性验证

本节按照不同轨道高度选择3颗激光星作为测试目标(北美防空司令部(NORAD)编目号分别为39452、36508和16908),雷达波束半宽设为0.025°,涉及到的时刻均为北京时间.

(1)轨道高度420 km的39452

用2021年3月12日4:21:50.766的TLE根 数,产生2021年3月16日3:45–3:54过境区间的引导数据,预报时长约为4 d.所选的比对点历元时刻为2021年3月16日3:48:01.000,方 位 角350.0074°、仰 角20.7434°、斜 距1026455.67 m.搜 索 仰 角hs设 为20.7434°,最大沿迹误差范围预估为±20 s,子区间的重叠比例设为20%.表1是两种方法预报约4 d的部分引导数据,其中等仰角搜索(Constant Elevation Search,CES)部分列出了雷达波束沿指定仰角hs搜索的3个连续驻留波束,Begin time和End time分别代表波束驻留的开始时间和结束时间,A1表示驻留波束中心指向的方位角,ρ1表示驻留波束中心指向上的目标距离.比对点历元时刻3:48:01.000在时间区间3:48:00.425–3:48:02.109内,则此驻留波束(底色加粗标出)就是我们需要查找的波束,其中心指向偏差θ1为0.0084°,小于波束半宽0.025°,表明本方法有效;点 位 预 报 部 分 则 列 出 了2021年3月16日3:48:01.000的点位(底色加粗标出),A2、h2和ρ2分别表示预报的方位角、仰角和斜距,其指向偏差θ2为0.0943°,明显超过波束半宽,表明点位预报失效.

(2)轨道高度750 km的36508

用2021年2月14日05:18:53.121的TLE根数,产生2021年3月1日13:08–13:19过境区间的引导数据,预报时长约为15 d.所选的比对点历元时刻为2021年3月1日13:11:56.000,方 位 角57.0719°、仰角19.0593°、斜距1665191.62 m.搜索仰角hs设为19.0593°,最大沿迹误差范围预估为±30 s,子区间的重叠比例亦设为20%.表2是两种方法预报约15 d的部分引导数据,表中各参数意义同表1.比对点历元时刻13:11:56.000在时间区间13:11:55.789–13:11:57.075内,则此驻留波束(底色加粗标出)就是我们需要查找的波束,其中心指向偏差θ1为0.0066°,小于波束半宽0.025°,表明本方法有效;而点位预报的指向偏差θ2为0.1560°(底色加粗标出),明显超过波束半宽,表明点位预报失效.

(3)轨道高度1400 km的16908

利用2020年10月16日05:25:16.146的TLE根数,产 生2021年3月1日13:29–13:49过 境 区 间 的 引 导数据,预报时长约为4个半月.所选的比对点历元时刻为2021年3月1日13:34:17.000,方位角190.1323°、仰角25.0861°、斜距2624898.24 m.搜索仰角hs设为25.0861°,最大沿迹误差范围预估为±100 s,子区间的重叠比例亦设为20%.表3是两种方法预报约4个半月的引导数据,表中各参数意义同表1、表2.比对点历元时刻13:34:17.000在时间区间13:34:15.945–13:34:19.519内,则此驻留波束(底色加粗标出)就是我们需要查找的波束,可以看出其中心指向偏差θ1为0.0122°,小于波束半宽,表示本方法有效;而点位预报的指向偏差θ2为1.8880°(底色加粗标出),远远超出了波束半宽,表明点位预报失效.

表1 39452的部分引导数据对比(预报约4 d)Table 1 Comparison of selected guidance data for 39452(predict about 4 days)

表2 36508的部分引导数据对比(预报约15 d)Table 2 Comparison of selected guidance data for 36508(predict about 15 days)

表3 16908的部分引导数据对比(预报约4个半月)Table 3 Comparison of selected guidance data for 16908(predict about 4.5 months)

从以上3个计算实例可以看出,在点位预报失效的情况下,等仰角搜索方法均有效,对所选轨道高度的目标均适用;且目标越高,采用等仰角搜索方法的根数有效预报时间越长.同时需要说明的是,雷达跟踪探测时对斜距引导数据的精度也有一定要求,一般是公里量级.表1–3中底色标出的引导数据中,点位预报的斜距误差分别为4279.87 m、2690.67 m、69029.30 m;而对应的等仰角搜索方法斜距误差分别为402.62 m、121.26 m、266.12 m,均显著优于点位预报.

3.2.2 效果对比

对于39452、36508和16908,分别选取2021年3月16日3:47:52.000–3:48:10.000、2021年3月1日13:11:47.000–13:12:05.000和2021年3月1日13:34:08.000–13:34:26.000这3个各19 s的时间段,以对比的方式直观展示两种方法的效果,结果分别如图4、图5和图6所示;纵坐标代表指向偏差,其中红线表示等仰角搜索驻留波束的中心指向与同时刻比对数据的站心观测矢量的偏差,紫线表示点位预报的站心观测矢量与同时刻比对数据的站心观测矢量的偏差,平行于横坐标的绿线表示波束半宽0.025°.由图4(a)、图5(a)和图6(a)可以看出,3个目标的点位预报的指向偏差均超出波束半宽,代表这19 s的点位预报结果均失效;图4(b)、图5(b)和图6(b)分别是图4(a)、图5(a)和图6(a)中等仰角搜索算法效果的局部放大,图中CES方法预报的观测指向偏差在搜索过程中存在一段优于0.025°的短时区间,代表目标可在此时被驻留波束观测到.

图4 指向偏差对比—39452.(a)19 s过境弧段,(b)等仰角搜索效果局部放大.Fig.4 Comparison of pointing deviation—39452.(a)19 s of transit arc,(b)Zoom in to show CES results.

图5 指向偏差对比—36508.(a)19 s过境弧段,(b)等仰角搜索效果局部放大.Fig.5 Comparison of pointing deviation—36508.(a)19 s of transit arc,(b)Zoom in to show CES results.

图6 指向偏差对比—16908.(a)19 s过境弧段,(b)等仰角搜索效果局部放大.Fig.6 Comparison of pointing deviation—16908.(a)19 s of transit arc,(b)Zoom in to show CES results.

3.2.3 结果统计

本节通过更多算例来验证等仰角搜索方法的有效性.继续选取3个目标其他若干个过境区间以同样的方法进行对比,结果如表4所示,其中A0、h0和ρ0分别表示比对数据的方位角、仰角和斜距.最大沿迹误差范围仍分别设为±20 s、±30 s和±100 s,预报的时间仍分别为4 d、15 d和4个半月,等仰角搜索所用的仰角值即各比对点站心系观测量的仰角值(底色加粗标出),试算过程中根据需要将子区间重叠比例调整为20%–30%不等,波束半宽仍然为0.025°.从表4的共计25次算例结果中可以看出,基于相同的TLE根数,点位预报全部失败,而等仰角搜索方法均能成功.

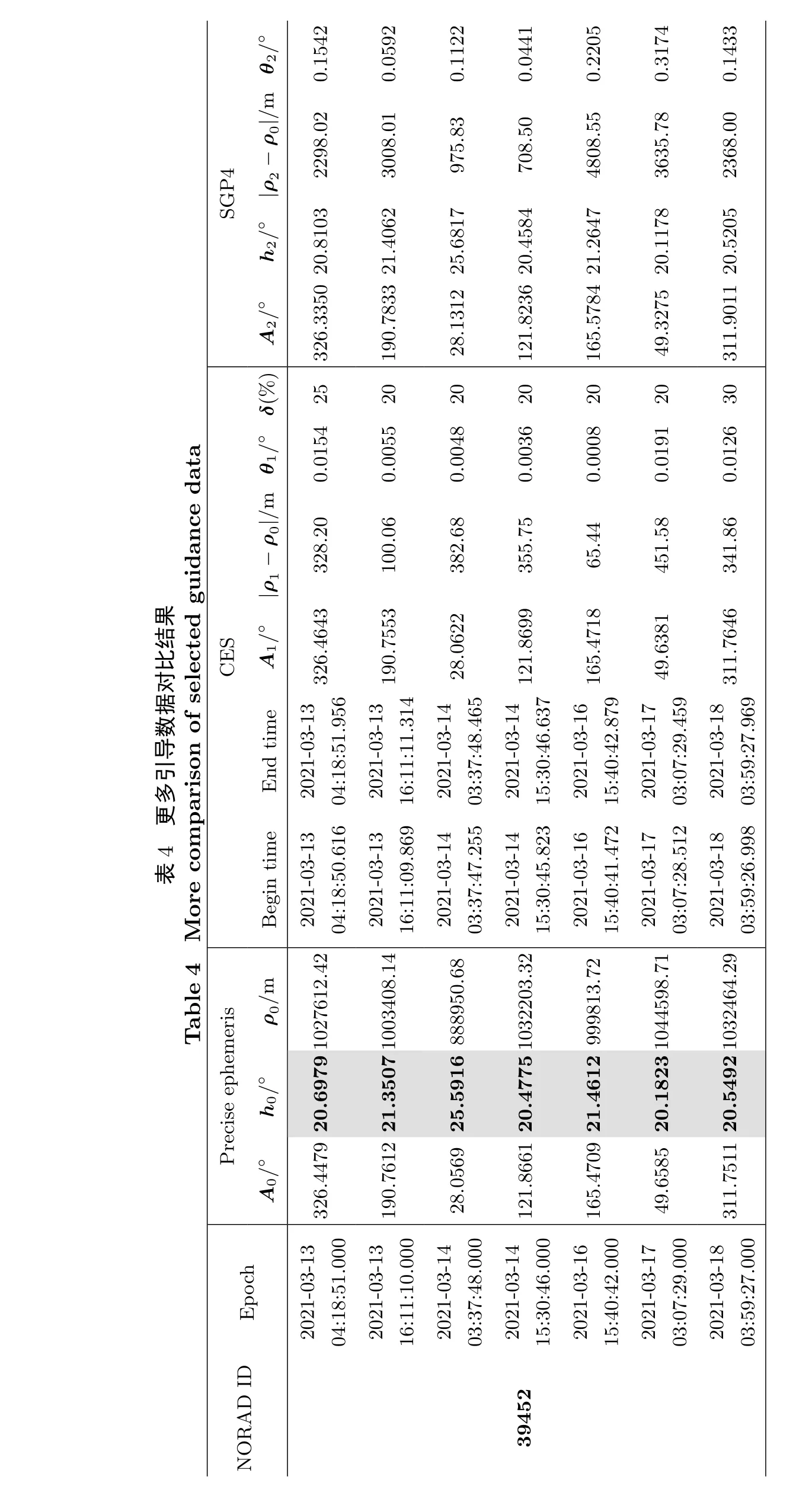
表4更多引导数据对比结果Table 4 M ore com parison of selected guidance data NORAD ID Epoch Precise ephemeris CES SGP4 A0/°h0/°ρ0/m Begin time End time A1/° |ρ1-ρ0|/m θ1/° δ(%)A2/°h2/° |ρ2-ρ0|/m θ2/°39452 2021-03-13 04:18:51.000 326.4479 20.6979 1027612.42 2021-03-13 04:18:50.616 2021-03-13 04:18:51.956 326.4643 328.20 0.0154 25 326.3350 20.8103 2298.02 0.1542 2021-03-13 16:11:10.000 190.7612 21.3507 1003408.14 2021-03-13 16:11:09.869 2021-03-13 16:11:11.314 190.7553 100.06 0.0055 20 190.7833 21.4062 3008.01 0.0592 2021-03-14 03:37:48.000 28.0569 25.5916 888950.68 2021-03-14 03:37:47.255 2021-03-14 03:37:48.465 28.0622 382.68 0.0048 20 28.1312 25.6817 975.83 0.1122 2021-03-14 15:30:46.000 121.8661 20.4775 1032203.32 2021-03-14 15:30:45.823 2021-03-14 15:30:46.637 121.8699 355.75 0.0036 20 121.8236 20.4584 708.50 0.0441 2021-03-16 15:40:42.000 165.4709 21.4612 999813.72 2021-03-16 15:40:41.472 2021-03-16 15:40:42.879 165.4718 65.44 0.0008 20 165.5784 21.2647 4808.55 0.2205 2021-03-17 03:07:29.000 49.6585 20.1823 1044598.71 2021-03-17 03:07:28.512 2021-03-17 03:07:29.459 49.6381 451.58 0.0191 20 49.3275 20.1178 3635.78 0.3174 2021-03-18 03:59:27.000 311.7511 20.5492 1032464.29 2021-03-18 03:59:26.998 2021-03-18 03:59:27.969 311.7646 341.86 0.0126 30 311.9011 20.5205 2368.00 0.1433

表4续Table 4 Continued NORAD ID Epoch Precise ephemeris CES SGP4 A0/°h0/°ρ0/m Begin time End time A1/° |ρ1-ρ0|/m θ1/° δ(%)A2/°h2/° |ρ2-ρ0|/m θ2/°36508 2021-02-26 01:52:39.000 164.7270 19.9910 1615163.53 2021-02-26 01:52:38.914 2021-02-26 01:52:41.090 164.7296 108.77 0.0025 20 164.7452 19.9440 418.60 0.0500 2021-02-26 14:02:50.000 9.0557 20.1226 1615592.52 2021-02-26 14:02:48.838 2021-02-26 14:02:51.509 9.0356 488.15 0.0189 20 9.0272 20.1094 3511.31 0.0299 2021-02-27 02:42:35.000 233.9054 21.0283 1570246.90 2021-02-27 02:42:34.060 2021-02-27 02:42:35.415 233.9228 147.36 0.0163 20 233.8508 20.9611 619.33 0.0843 2021-02-27 14:52:41.000 311.9426 19.9552 1623483.70 2021-02-27 14:52:40.863 2021-02-27 14:52:42.304 311.9587 136.67 0.0151 20 312.0776 19.9468 3276.08 0.1272 2021-02-28 01:50:42.000 169.3057 20.1195 1608693.13 2021-02-28 01:50:40.740 2021-02-28 01:50:42.929 169.3261 182.86 0.0192 20 169.3392 20.0113 2296.58 0.1126 2021-02-28 14:00:53.000 5.3266 20.0568 1619447.30 2021-02-28 14:00:51.240 2021-02-28 14:00:53.921 5.3098 506.44 0.0158 20 5.3021 20.0115 4925.60 0.0508 2021-03-01 02:40:50.000 239.0533 19.9314 1617351.33 2021-03-01 02:40:49.675 2021-03-01 02:40:50.926 239.0463 56.55 0.0066 20 238.9267 19.8459 1562.58 0.1466 2021-03-02 01:48:45.000 173.9026 20.0870 1609437.39 2021-03-02 01:48:43.230 2021-03-02 01:48:45.430 173.8807 75.22 0.0205 20 173.9273 19.9575 3299.84 0.1316 2021-03-02 13:58:57.000 1.6247 20.0008 1622884.80 2021-03-02 13:58:54.647 2021-03-02 13:58:57.226 1.6180 440.50 0.0062 25 1.6165 19.9457 5175.39 0.0556

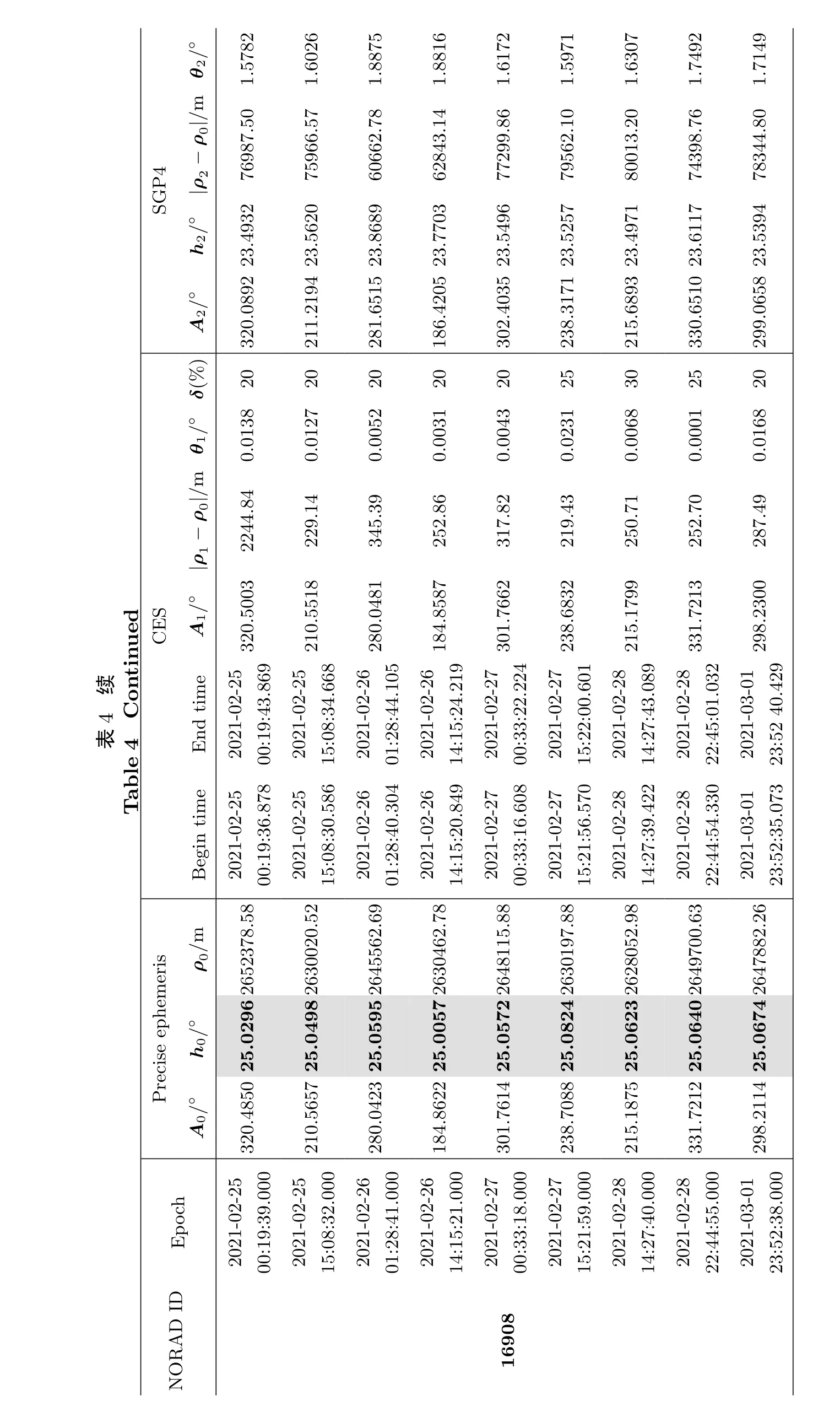
表4续Table 4 Continued NORAD ID Epoch Precise ephemeris CES SGP4 A0/°h0/°ρ0/m Begin time End time A1/° |ρ1-ρ0|/m θ1/° δ(%)A2/°h2/° |ρ2-ρ0|/m θ2/°16908 2021-02-25 00:19:39.000 320.4850 25.0296 2652378.58 2021-02-25 00:19:36.878 2021-02-25 00:19:43.869 320.5003 2244.84 0.0138 20 320.0892 23.4932 76987.50 1.5782 2021-02-25 15:08:32.000 210.5657 25.0498 2630020.52 2021-02-25 15:08:30.586 2021-02-25 15:08:34.668 210.5518 229.14 0.0127 20 211.2194 23.5620 75966.57 1.6026 2021-02-26 01:28:41.000 280.0423 25.0595 2645562.69 2021-02-26 01:28:40.304 2021-02-26 01:28:44.105 280.0481 345.39 0.0052 20 281.6515 23.8689 60662.78 1.8875 2021-02-26 14:15:21.000 184.8622 25.0057 2630462.78 2021-02-26 14:15:20.849 2021-02-26 14:15:24.219 184.8587 252.86 0.0031 20 186.4205 23.7703 62843.14 1.8816 2021-02-27 00:33:18.000 301.7614 25.0572 2648115.88 2021-02-27 00:33:16.608 2021-02-27 00:33:22.224 301.7662 317.82 0.0043 20 302.4035 23.5496 77299.86 1.6172 2021-02-27 15:21:59.000 238.7088 25.0824 2630197.88 2021-02-27 15:21:56.570 2021-02-27 15:22:00.601 238.6832 219.43 0.0231 25 238.3171 23.5257 79562.10 1.5971 2021-02-28 14:27:40.000 215.1875 25.0623 2628052.98 2021-02-28 14:27:39.422 2021-02-28 14:27:43.089 215.1799 250.71 0.0068 30 215.6893 23.4971 80013.20 1.6307 2021-02-28 22:44:55.000 331.7212 25.0640 2649700.63 2021-02-28 22:44:54.330 2021-02-28 22:45:01.032 331.7213 252.70 0.0001 25 330.6510 23.6117 74398.76 1.7492 2021-03-01 23:52:38.000 298.2114 25.0674 2647882.26 2021-03-01 23:52:35.073 2021-03-01 23:52 40.429 298.2300 287.49 0.0168 20 299.0658 23.5394 78344.80 1.7149

3.3 波束宽度探索

上文已验证等仰角搜索算法的有效性,其在点位预报失效时仍能搜索捕获到目标.在此基础上,本节逐渐缩小有效波束半宽,探索等仰角搜索4 d左右(最大沿迹误差均设置为±20 s)能够成功的波束半宽下限.探索过程中根据需要适当调整重叠比例因子δ,且若计算出的波束驻留时间接近1 s,则不再继续探索.表5汇总了3个目标共计28组试算成功的最窄有效波束宽度的等仰角搜索结果,bhw表示波束半宽,搜索仰角以及比对点站心系观测量同3.2节,且仅列出成功搜索到比对点的驻留波束引导数据.根据表5中3目标不同过境弧段的波束半宽下限试算结果可估计,基于TLE根数时,在波束驻留时间接近1 s的情况下,对39452目标,有效波束半宽下限约0.0222°(均值);对36508目标,有效波束半宽下限约0.0151°(均值);对16908目标,有效波束半宽下限约0.0062°(均值),可以看出轨道高度越高,可试算成功的波束半宽下限越小.

表5 续Table 5 Continued

4 结论

本文基于沿迹误差补偿的思想,提出了一种适用于窄波束雷达捕获空间目标的等仰角搜索方法,仿真结果表明,该方法在点位预报失败的情况下能成功捕获目标,且轨道高度越高的目标,可成功探测的最窄波束宽度越小.本文研究工作具有以下特点:

(1)区别于点位预报方法,通过预估沿迹误差范围将不确知的沿迹误差转化成了可精确计算的搜索范围,并通过精密轨道计算得到引导数据,引导雷达波束在指定的仰角上单向调整波束指向的方位角,为窄波束雷达或其他窄视场设备的目标捕获提供了一条新的技术途径;

(2)通过适当重叠子区间削弱了相对于沿迹误差均为小量且随预报时间增长缓慢的法向误差和径向误差的影响,充分保障可靠性的同时还允许预报更长的时间.

由于目标在被搜索到以后很快便会偏离雷达视场,为了获得更加充足的观测资料,还需要继续探索本文方法应用于窄视场观测设备时的工作模式,特别是如何由捕获转入跟踪的技术方法,使得观测设备能够“捕获”并“跟踪”目标,这是我们后续的工作之一.