用GeoGebra软件探究“追逐之路”
——图解第38届物理竞赛预赛中的多人追逐问题
鲍吴兵 谢恩东
(安庆市第一中学 安徽 安庆 246003)
1 多人追逐问题
【例1】(第38届全国中学生物理竞赛预赛第13题) 6个小朋友在操场上玩追逐游戏.开始时,6个小朋友两两间距离相等,构成一正六边形.然后每个小朋友均以不变的速率v追赶前面的小朋友(即小朋友1追2,2追3,3追4,4追5,5追6,6追1),在此过程中,每个小朋友的运动方向总是指向其前方的小朋友.已知某一时刻t0=0,相邻两个小朋友的距离为l,如图1所示.试问:
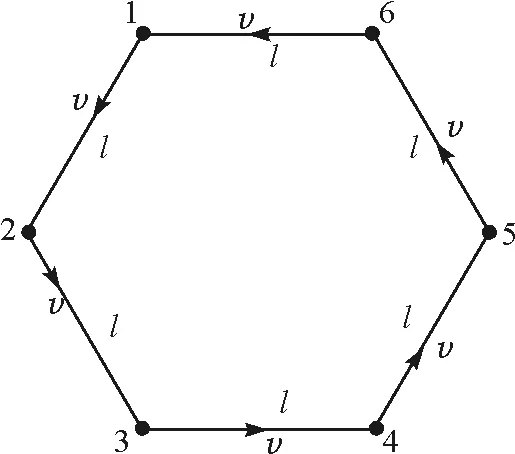
图1 例1题图
(1)从t0时刻开始,又经过多长时间后面的小朋友可追到前面的小朋友?
(2)从t0时刻开始,直至追上前面的小朋友,每个小朋友又跑了多少路程?
(3)在t0时刻,每个小朋友的加速度大小是多少?
以上问题中物体B始终正对物体A以一定速率追逐A,由于物体B的运动取决于物体A的位置,这类问题通常比较复杂,很难用方程直接表述B的轨迹,我们可用电脑软件辅助处理,但有些软件专业要求较高[1],令多数教师望而却步.GeoGebra软件是一款动态几何软件,其“向量”功能可很好地表达上述问题中的“物体B始终正对物体A”的速度方向问题,下面以任意N个质点为例,介绍GeoGebra软件如何实现“追逐之路”.
2 用GeoGebra软件描绘轨迹
如图2所示,有N(N≥ 3)个人P1,P2,…,PN,分别位于边长为L的正N边形的各顶点上,这N个人从某时刻开始按逆时针依次追击,即P1追P2,P2追P3,…,PN-1追PN.

图2 人的初始位置
(1)引入变量.用滑动条N表示人的数量,滑动条v表示人的速度大小,滑动条t表示时间;
(2)描点.标出坐标原点O,描点P1表示人,指令栏输入:P_2=旋转(P_1, (360°)/N,O),用正多边形工具作出过点P1和P2各点的正N边形,作图过程与效果如图3所示;

图3 作图过程与效果
(3)设置速度.在指令栏输入:单位向量(向量(P_1,P_2)),得到P1追P2方向上的单位向量u,u是辅助对象可隐藏,再输入:向量(P_1,P_1 + 0.3vu),得到的向量w能动态显示速度大小、方向的变化;
(4)设置运动.在滑动条t的脚本区输入代码:赋值(P_1,P_1+0.01vu),如图4所示,此代码表示在时间t更新时P1的位置会按设定的速度变化,启动滑动条t的动画就可看到相互追逐的运动;

图4 脚本代码
(5)显示轨迹.隐藏不必要对象,设置对象的相关属性,并显示点的轨迹,就可得到追逐路径,如图5和图6所示.
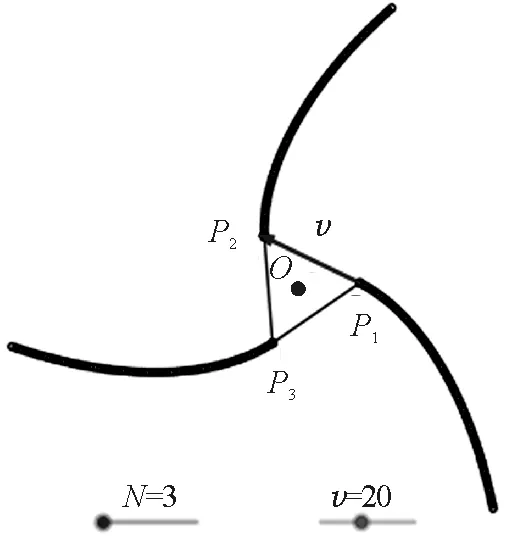
图5 3人追逐
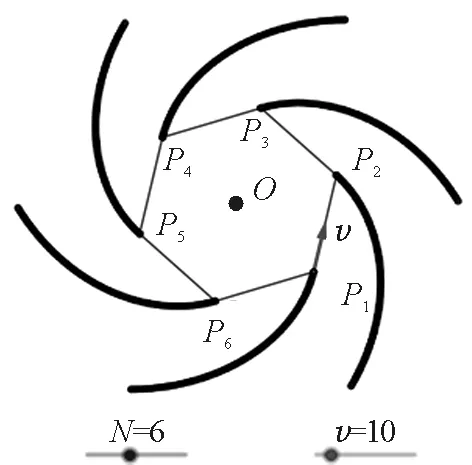
图6 6人追逐
3 拓展应用
按以上方法还可以实现多种追逐问题的轨迹,图7是速度较小的物体B追逐速度较大的匀速圆周运动的物体A的部分轨迹.由于物体B速度较小,不可能追上物体A,经足够长时间后物体B将做半径较小的圆周运动,如图8所示.图9是模拟导弹的拦截过程,速度较小的导弹A(视为斜抛)被速度较大的导弹B击中.
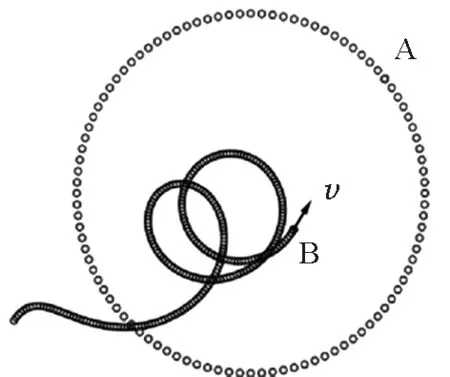
图7 追逐圆周运动的过程

图8 追逐圆周运动的终态

图9 导弹的拦截过程

