泊松截断δ冲击模型冲击参数的Bayes估计*

彭博，马明，拉毛措，冶建华

(西北民族大学数学与计算机科学学院，甘肃 兰州 730030)

引言

截断δ冲击模型是以冲击时间间隔为失效机制的可靠性模型. 该模型是指在一个遭受间歇性冲击的系统中，如果经过某次冲击之后，超过δ长的时间还没有冲击到达，则系统失效[1].

目前关于截断δ冲击模型的文章有很多. 文献[2]～[6]分别得到了泊松截断δ冲击模型相关参数的极大似然估计、(0,b)均匀截断δ冲击模型、(a,b)均匀截断δ冲击模型相关参数的极大似然估计和Bayes估计. 文献[7]与文献[8]分别研究了时间点服从0-1分布的截断δ冲击模型、离散弱更新下幂级数开型截断δ冲击模型的寿命分布、平均寿命这两类可靠性指标. 文献[9]与文献[10]分别得到了格点更新截断δ冲击模型、非负几何离散开型截断δ冲击模型的寿命分布、平均寿命、失效率、可靠度等可靠性指标. 文献[11]讨论了截断δ冲击模型的标值过程，得到了截断δ冲击模型的标值过程的二阶矩，并将结果应用于客户寿命价值的二阶矩中. 文献[12]将泊松截断δ冲击模型应用到不完全维修更换策略，建立了N型不完全维修更换策略模型.

本文讨论了泊松截断δ冲击模型冲击参数的(多层)Bayes估计. 首先给出了模型和两类样本观测数据. 其次讨论了基于两类样本数据，冲击参数λ的先验分布分别是伽马先验、伽马均匀多重先验和Jeffreys先验情形下的Bayes估计和多层Bayes估计.

1 模型及样本观测数据

考虑一个遭受外部冲击的单元件系统，该系统的寿命遵循冲击参数为λ，失效参数为δ的泊松截断δ冲击模型[1]，对该系统的冲击情况进行观测，假设分别观测到以下两类样本数据[2],分别记为A1与A2.

A1：观测到该系统在失效时总共冲击次数为m，m≥0.

A2：不仅观测到该系统失效时总共的冲击次数m，若m≠0，则还观测到冲击到达时间t1,t2,…,tm,m=1,2,…，其中ti,i=1,2,…,m是观测到的第i次冲击到达时刻，且tm是系统失效前最后一次冲击时刻.

2 主要结果

2.1 基于样本数据A1的λ的参数估计

由文献[2]可知泊松截断δ冲击模型基于样本数据A1的似然函数为

(1)

基于样本数据A1可得当δ已知时λ的Bayes估计.

定理1设λ的先验分布是形状参数为α，尺度参数为β的伽马分布，且α,β,δ均已知，则基于样本数据A1，在最小均方误差原则下，λ的Bayes估计为

(2)

证明因为λ的先验分布是形状参数为α，尺度参数为β的伽马分布，所以λ的先验密度函数为

(3)

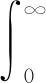
由(3)式与(1)式可得λ的后验密度函数为

(4)

因此在最小均方误差原则下λ的Bayes估计为

(5)

下面需要判断(5)式的敛散性.

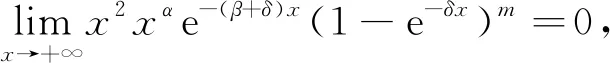
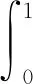
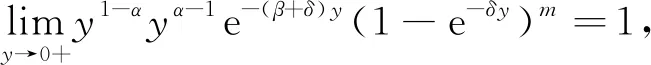
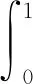
根据定理1可以推出当系统失效时没有冲击到达情形下λ的估计.

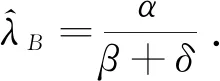
证明 若观测到系统失效时没有冲击到达，则由(2)式得λ的Bayes估计为

(6)

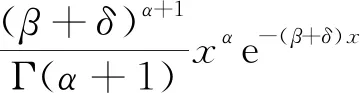
(7)

同理可得

(8)

下面定理得到了当δ已知时，基于样本数据A1，在最小均方误差原则下，λ的先验分布是Jeffreys先验时冲击参数λ的Bayes估计. Jeffreys先验是在未知参数的先验分布是未知的情形下，利用似然函数的Fisher信息量获得先验分布的一种先验确定方法.

定理2设λ的先验分布是Jeffreys先验，且δ已知，则基于样本数据A1，在最小均方误差原则下，λ的Bayes估计为

证明样本数据A1的似然函数为(1)式，对数化(1)式得lnL(m|λ)=mln(1-e-λδ)-λδ，

所以似然函数L(m|λ)的Fisher信息量为

其中M是系统失效时可能遭受的总冲击次数，样本数据A1中的m是M的一个实现，且易知M的概率分布列是(1)式中的似然函数.

易得

(9)

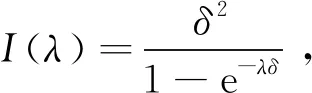
(10)

由(10)式与(1)式得λ的后验密度函数为

则在最小均方误差原则下，λ的Bayes估计为

(11)

定理得证.

定理3设λ服从参数是c1,c2的伽马均匀多重先验，则基于样本数据A1，在最小均方误差原则下，λ的多层Bayes估计为

证明因为λ服从形状参数为α，尺度参数为β的伽马分布，所以可得λ的第一层先验密度函数为

又因为α,β分别服从(0,c1),(0,c2)上的均匀分布，且α与β相互独立，则可得超参数(α,β)的超先验密度为

因此λ的多层先验密度函数fλ(s)为

(12)

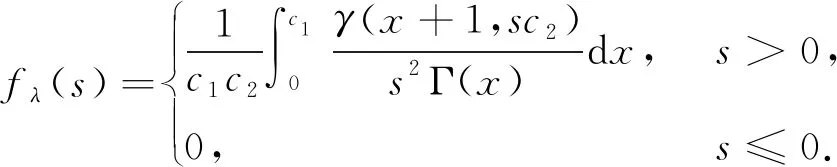
(13)

由(13)式与(1)式得λ的后验密度函数为

因此在最小均方误差原则下λ的多层Bayes估计为

定理得证.

由定理3可得当系统失效时没有冲击到达情形下λ的多层Bayes估计.

推论2 设λ服从参数是c1,c2的伽马均匀多重先验，若观测到系统失效时没有冲击到达，则在最小均方误差原则下，λ的多层Bayes估计为

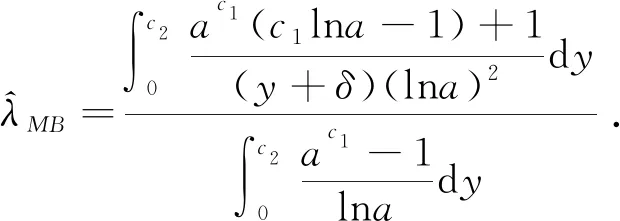
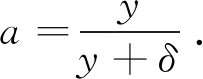
证明 由定理3可知,当系统失效时没有冲击到达时λ的多层Bayes估计为

由(7)式及(8)式可知

因此

(14)

所以

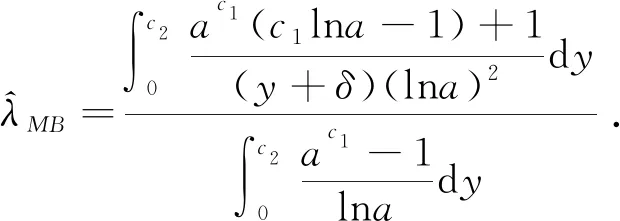
推论得证.

2.2 基于样本数据A2的λ的参数估计

由文献[2]可知泊松截断δ冲击模型样本数据A2的似然函数为

(15)

其中m=0,1,2,…，对∀m≥1，有0

定理4设λ的先验分布是形状参数为α，尺度参数为β的伽马分布，且α,β,δ均已知，则基于样本数据A2，在最小均方误差原则下，λ的Bayes估计为

证明由λ的先验密度(3)式与样本数据A2的似然函数(15)式可得λ的后验密度函数为

则在最小均方误差原则下λ的Bayes估计为

当系统失效时没有冲击到达情形下，由定理4也可直接得到推论1. 下面定理5给出在样本数据A2下λ的一个多重Bayes估计.

定理5设λ服从参数是c1,c2的伽马均匀多重先验，则基于样本数据A2，在最小均方误差原则下，λ的多层Bayes估计为

(16)

证明易知λ的多层先验密度函数仍如(12)式所述，则由(12)式与(15)式可得λ的后验密度函数为

由此可以得到最小均方误差原则下λ的多层Bayes估计

注意到

因此

定理得证.

作为定理5的一个验证，下面讨论推导当系统失效时没有冲击到达情形下λ的多层Bayes估计.

由(16)式可知，当系统失效没有冲击到达时λ的多层Bayes估计为

(17)

注意到(17)式与(14)式形式相同，因此推论2也是定理5的一个推论.

下面定理得到了当δ已知时，基于样本数据A2，在最小均方误差原则下，先验分布是Jeffreys先验时λ的Bayes估计.

定理6设λ的先验分布是Jeffreys先验，且δ已知，则基于样本数据A2，在最小均方误差原则下，λ的Bayes估计为

证明样本数据A2的似然函数为(15)式，对数化(15)式得

lnL(t0,t1,…,tm;m|λ)=mlnλ-λtm-λδ，

因此似然函数的Fisher信息量为

(18)

可以得到λ的后验密度函数为

则在最小均方误差原则下λ的Bayes估计为

(19)

下面需要判断(19)式的敛散性.

由于

所以由迫敛性可得

(20)

因此(19)式的分子部分收敛.

则由(20)式得

3 结语

本文主要研究了泊松截断δ冲击模型冲击参数的Bayes估计和多层Bayes估计，基于样本数据A1,A2和最小均方误差原则，分别在形状参数为α，尺度参数为β的Gamma分布、参数为c1,c2的伽马均匀多重先验和Jeffreys先验三种先验下，得到了冲击参数λ的Bayes估计量.

本文考虑的是单元件系统，未来可以讨论多元件系统的参数估计. 同时，A1、A2这两类样本数据是完全寿命数据，在可靠性试验中一般得到的是不完全数据，在今后可以研究本模型在不完全寿命数据下的参数估计.