Finite-Time Stability for Nonlinear Fractional Differential Equations with Time Delay
HE Huazhen(閤华珍), KOU Chunhai(寇春海)
College of Science, Donghua University, Shanghai 201620, China
Abstract: The finite-time stability and the finite-time contractive stability of solutions for nonlinear fractional differential equations with bounded delay are investigated. The derivative of Lyapunov function along solutions of the considered system is defined in terms of the Caputo fractional Dini derivative. Based on the Lyapunov-Razumikhin method, several sufficient criteria are established to guarantee the finite-time stability and the finite-time contractive stability of solutions for the related systems. An example is provided to illustrate the effectiveness of the obtained results.
Key words: finite-time stability; nonlinear fractional differential equation; time delay; Caputo fractional Dini derivative; Lyapunov-Razumikhin method
Introduction
Fractional calculus is an important extension of classical calculus. Due to the fact that many real systems have heredity and memory properties, fractional differential systems are more accurate in modeling the dynamic behaviors than traditional integer order differential systems. In the analysis of qualitative theory of differential systems, the stability of solutions is the primary consideration. Therefore, the stability of solutions is one of the most significant research topics for fractional differential systems with many results[1-5].
In the field of classic control theory, researchers usually pay attention to the Lyapunov stability. However, the finite-time stability (FTS), which was first introduced in the 1950s[6], only considered the changes of states of systems over a finite time interval. Recently, for the finite-time stability of fractional differential systems, some useful results have been obtained by using generalized Gronwall inequality[7-13], Hölder inequality and Cauchy-Schwartz inequality[14-15], Mittag-Leffler type matrix function[16-17], linear matrix inequalities[18]and so on. In 1967, Weiss and Infante[19]proposed a new concept, finite-time contractive stability (FTCS), which characterized not only the “boundedness”, but also the “contraction”. FTCS requires the system state to remain within a certain threshold in finite time and within a smaller specified bound before reaching the terminal time. Chengetal.[20]studied the finite-time contractive stability for a class of Markovian jump linear systems.
Since the middle of the 20th century, time-delay dynamics problems have appeared in many different fields, such as ecology, electric power, control engineering, and management systems, which may affect the stability of systems. The Lyapunov-Razumikhin method is an important method in studying the stability of delay differential systems. In the existing contributions, the Caputo fractional derivative is commonly adopted, which requires a continuously differentiable Lyapunov function[1, 21]. However, if we use the fractional Dini derivative in Caputo sense, Lyapunov function only needs to be continuous[22-24]. For this reason, it is naturally meaningful to study the finite-time stability for fractional delay differential equations by employing the fractional Dini derivative.
The rest of this paper is organized as follows. In section 1, some preliminaries about fractional calculus and finite-time stability are presented. In section 2, we give and prove the main results. An example to demonstrate the validity of the gotten results is given in section 3. In section 4, some conclusions are drawned.
1 Preliminaries
In this section, we will give some useful definitions and lemmas. Throughout this paper, we assumeα∈(0,1) and 0≤t0 Definition1[25]The Riemann-Liouville fractional derivative of orderα∈(0,1) for a functiong(t) is defined by Definition2[25]The Caputo fractional derivative of orderα∈(0,1) for a functiong(t) is defined by (1) The Riemann-Liouville fractional derivative and the Caputo fractional derivative are connected by the following relation: (2) The Caputo fractional derivative coincides with the Riemann-Liouville fractional derivative wheng(t0)=0 andg(t) satisfies certain conditions. Definition3[25]The Grünwald-Letnikov fractional derivative of orderα∈(0,1) for a functiong(t) is defined by and the Grünwald-Letnikov fractional Dini derivative of orderα∈(0,1) for a functiong(t) is defined by (3) Lemma1[26]Letα∈(0,1). Ifg∈C[t0,T], then for allt∈(t0,T], From Eqs. (2) and (3), we can define the Caputo fractional Dini derivative ofg(t) as i.e., (4) Consider the following fractional delay differential equations with Caputo fractional Dini derivative (5) In this paper, we assume that the functionfis that the corresponding system (5) has a unique solutionx(t;t0,φ0)∈Cα([t0,T],Rn) for any initial data (t0,φ0). Definition5[27]The system (5) is as follows. (1) Finite-time stable with respect to (c1,c2,T).If given three positive constantsT,c1, andc2withc1 (2) Finite-time contractive stable with respect to (c1,c2,η,σ,T).If given five positive constantsT,c1,c2,η, andσwithη As usual, we shall use the following function class: K={ω∈C(R,R): ω(s) is strictly increasing andω(0)=0}. Now, we introduce the following class of Lyapunov-like functions which will be used in the discussion. Definition6LetJ=[t0-τ,T] be a given interval and 0∈Δ⊂Rnbe a given set. We say that the functionV(t,x):J×Δ→R+belongs to the class Λ(J,Δ), ifV(t,x) is continuous onJ×Δand locally Lipschitzian with respect to its second argument andV(t,0)≡0. When we use Lyapunov function to study the stability of differential equations, the derivative of Lyapunov function along the solutions of differential equations require an appropriate definition. Here, we adopt the Caputo fractional Dini derivative which is given in Eq. (4) for fractional differential equations. Letm(θ)=x(t+θ),θ∈[-τ, 0]. The Caputo fractional Dini derivative of Lyapunov functionV(t,x)∈Λ(J,Δ) along the solutions of system (5) is defined by (6) i.e., (7) where for allt∈(t0,T), there existsht>0 such thatt-η∈J,m(0)-hαf(t,m)∈Δfor 0<η Next, we give an important lemma which will be used later. In this section, by using the Lyapunov-Razumikhin method, several sufficient criteria will be derived to guarantee the finite-time stability of the system (5). (ⅰ)ω1(‖x‖)≤V(t,x)≤ω2(‖x‖), ∀(t,x)∈(J,Δ); (ⅱ) fort∈[t0,T], wheneverV(t+s,m(s))≤Ψ(t,s)V(t,m(0)) fors∈[-τ, 0], where Then the system (5) is finite-time stable with respect to (c1,c2,T). (8) Let We have 0<η<1 and ∀t∈[t0-τ,T], whereεis an enough small positive constant which is Then we can get Now we prove thatΩε(t)≤V0,∀t∈[t0,T].Note thatt=t0,Ωε(t0)=V(t0)≤V0.So, if the above assertion does not hold, there ist*∈(t0,T] such thatΩε(t*)>V0, andΩε(t)≤V0fort∈[t0,t*). From Lemma 2, we obtain Then (9) Ωε(t)≤V0<Ωε(t*), ∀t∈[t0-τ,t*], which means that i.e., ∀t∈[t0-τ,t*]. (10) It follows that which implies that ∀s∈[-τ, 0]. Now we need to estimate the Caputo fractional Dini derivative ofΩε(t).For anyt∈(t0,t*],h>0, let From Eqs. (3)-(5), it follows that fort∈(t0,t*], the solutionx(t) satisfies the equalities and Hence, whenh→0, x(t)-hαf(t,xt)=H(x(t),h)+φ0(0)+o(hα) (11) holds. Then for anyt∈(t0,t*], we have (12) where (13) SinceV(t,x) is locally Lipschitzian with respect to its second argument with a Lipschitz constantL>0, we get (14) (15) Sett=t*. We have By the condition (ⅱ), we obtain (16) Thus (17) By the conditions (ⅰ) and (ⅲ) and formula (17), we obtain that when ‖φ0‖τ (18) for anyt∈[t0,T], which implies that ‖x(t)‖ Theorem2Assume that there exist positive constantsc1,c2,η,σ, andTwithη Then system (5) is finite-time contractive stable with respect to (c1,c2,η,σ,T). ProofFrom Theorem 1, we know if ‖φ0‖τ ω1(‖x(t)‖)≤V(t,x(t))≤ (19) which implies that ‖x(t)‖<η,∀t∈[T-σ,T]. Corollary1Lett0=0.Assume that there exist positive constantsc1,c2,η,σ,T,λ,ω1,ω2, andawithη 1)ω1‖x‖a≤V(t,x)≤ω2‖x‖a, ∀(t,x)∈(J,Δ); 2) for allt∈[0,T], wheneverV(t+s,m(s))≤exp(λτ)V(t,m(0)) fors∈[-τ, 0]; Then the system (5) is finite-time stable with respect to (c1,c2,T). In this section, we give an example to illustrate the effectiveness of the above results. Consider the initial value problem (IVP) for the scalar delay fractional differential equations (20) wherex∈R,φ0∈C([-1,0],R). The IVP for the scalar fractional differential equations (20) with zero initial function has a zero solution. (ⅲ) For anyt∈[0, ln 2] ands∈[-1, 0], whenever [m(s)]2≤e[m(0)]2, we have Hence, from Corollary 1, system (20) is finite-time stable with respect to (1, 2, ln 2). In this paper, we study finite-time stability and finite-time contractive stability of nonlinear nonautonomous fractional delay differential equations. The Caputo fractional Dini derivative is adopted to define the derivative of the Lyapunov function along the solutions of the given system. Moreover, we extend the Lyapunov-Razumikhin method for finite-time stability from integer order delay differential equations to fractional delay differential equations. Then several sufficient criteria for finite-time stability are obtained.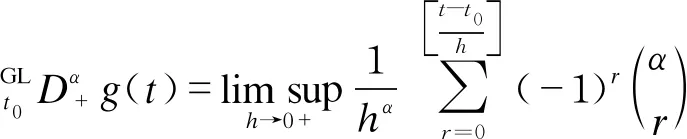



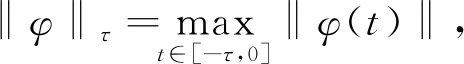


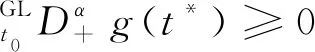
2 Main Results
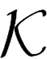
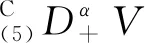
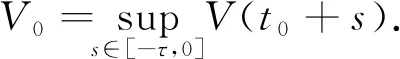



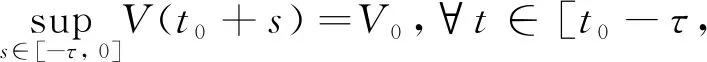
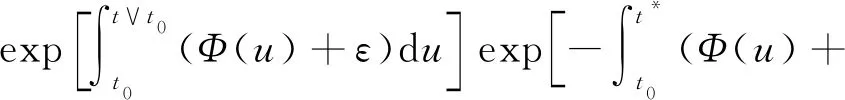

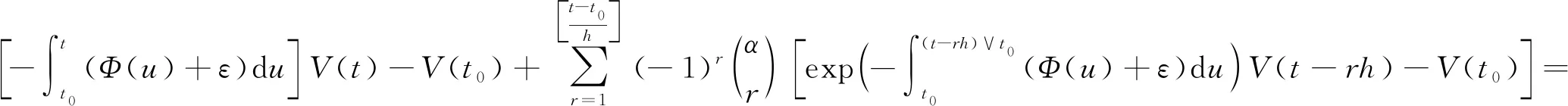
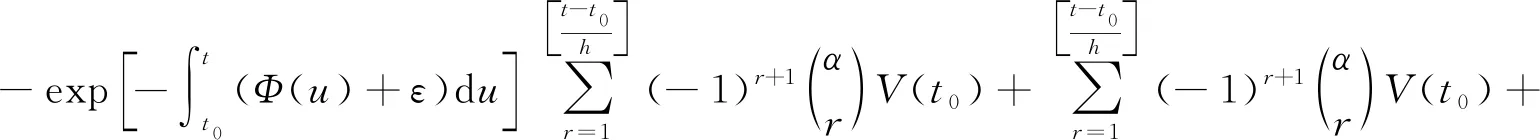

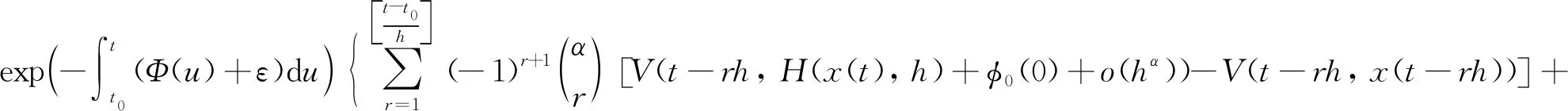

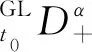
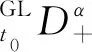
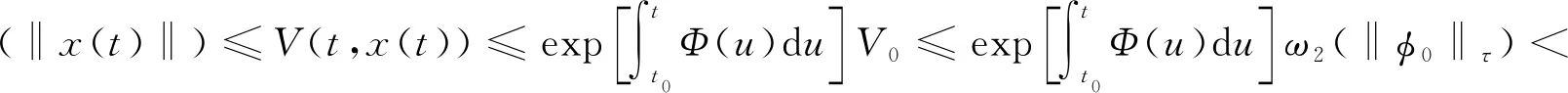

3 Examples
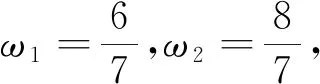



4 Conclusions
 Journal of Donghua University(English Edition)2022年5期
Journal of Donghua University(English Edition)2022年5期
