基于大概念的单元教学设计——以“平面向量”单元为例

江苏师范大学 刘 娜 吴晓红

基于大概念的单元教学设计已经成为当前学者们研究的热点话题。《普通高中数学课程标准（2017年版2020年修订）》指出，教师在进行教学设计时应以大概念为核心，以主题为引领，优化单元知识，统整零碎的知识，突出知识之间的逻辑关系，培养学生的实践能力，让学生形成数学观念，提高学生解决问题的能力，助力学科核心素养的落实。那么，如何进行基于大概念的单元教学设计呢？现以“平面向量”单元为例，探讨基于大概念进行单元整体教学设计的路径。

一、基于大概念的单元教学的内涵

大概念，也称为“核心概念”“大观念”等，起源于国外，具有较长的研究历史。布鲁纳提出的“一般概念”，具有大概念的影子。埃里克森认为大概念是一种概念性的工具，对于学生今后的生活具有指导性作用。威金斯和麦克泰格认为大概念是学科中较为核心的概念，常常表现为概念、观点、有争议的论点、问题等。顿继安、何彩霞认为大概念具有高度的聚合性，是学科的核心，能够将更多相关的知识联系起来，具有可持续迁移性。依据大概念范围和大小的不同，可将其依次划分为单元大概念、学科大概念、跨学科大概念以及哲学大概念。

基于大概念的单元教学设计，是教师基于课程标准的要求，将单元内容划分成若干个小单元，提炼出各个小单元的大任务与单元大概念，再以大概念为核心，基于学生已有的认知基础，选择并整合单元知识，引导学生把握知识背后所蕴含的思想方法，构建知识网络图。通过整体设计、实施，帮助学生获取系统的知识，促进学生的深度学习，让学生从整体上把握学科知识、学科逻辑、学科本质，形成有意义且可迁移的知识体系。较为典型的以大概念为中心的单元教学设计的路径主要有“逆向教学设计”与“科学—写作启发式教学设计”。研究借鉴“逆向教学设计”理论，即“目标—评价—教学”，探析以学科核心素养为导向，基于单元大概念的单元整体教学设计的路径。

二、基于大概念的单元教学路径

依据“逆向教学设计”理论，结合国内外学者对大概念和单元教学的研究成果，尝试提出基于大概念的单元教学设计的教学路径（见图1）。该模式有前期分析与开发设计两个环节。前期分析阶段主要有三个步骤：首先，结合课程标准对教材内容整体进行分析，提炼单元大概念；其次，依据大概念制定单元教学目标；最后，制定与单元教学目标相匹配的评估依据。开发设计环节是依据前期的分析设计相应的学习问题、学习活动。现以“平面向量”单元为例，通过对课程标准和“平面向量”单元知识内容的分析，提取单元大概念，制定单元教学目标、评估依据，设计单元任务，制定核心问题、基本问题。

图1 基于大概念的单元教学设计路径

（一）提炼单元大概念

对于提炼大概念的具体实施路径，邵卓越、刘徽等提出了两种路径：一是自上而下的方法，即从课程标准、学科核心素养等方面提取；二是自下而上的方法，即从生活价值、知能目标等方面提取。由于不同的学科具有不同的学科特征，因此在提炼大概念时要聚焦学科视角。现以“平面向量”单元为例，从知识技能出发，思考具体知识背后蕴含的思想方法，进而凝练成单元大概念。

依据知识的逻辑关系将“平面向量”单元分为四个小单元，依次为“向量的概念”“向量的运算”“向量的定理以及坐标表示”“向量的应用”。对于“向量的概念”，围绕“向量是一种怎样的数学工具”这一大任务，探究向量的特征、表示以及向量的性质，揭示了用数学的观点刻画和研究现实事物的方法和途径；对于“向量的运算”，围绕“如何借助代数运算刻画几何对象？”这一大任务，揭示几何直观与代数运算之间的关系；对于“向量的定理以及坐标表示”，围绕“如何表示平面内任意向量？”这一大任务，给出了用代数方法论证几何关系的数学方法；对于“向量的应用”，围绕“用向量法解决问题”这一大任务，利用向量列出图形中元素的相等关系式，将代数运算与几何图形融为一体。因而本单元内容的纵向逻辑可以理解为“概念—运算—代数运算与图形运算之间的关系—应用—研究平面向量的整个过程”。若按照这一纵向逻辑来进行教学，那么学生掌握的就是向量的概念、运算、定理等分散性的知识，难以形成系统的知识体系。因此，我们还需要从纵向的角度对教材进行解读，在此基础上建构起教与学的单元大概念。

依据上述分析，得到了四个小单元的大任务，且都围绕着“利用代数运算解决几何问题”进行教学，揭示了代数运算与几何直观之间的关系。在厘清四个小单元之间的关系之后，结合课程标准对本单元的要求——理解平面向量的几何意义和代数意义，掌握平面向量的概念、运算、定理以及向量的应用，用向量法解决问题等，概括出“平面向量”的单元大概念：建立向量模型及简化可以用代数运算描述几何图形的规律。以此为核心，设计指向核心素养的单元教学目标，为学生构建大概念下的教学过程。

（二）确定基于大概念的单元教学目标

单元教学目标为学生的学习起到指向性作用，是单元大概念的具体化。制定单元教学目标时需要依据学情，分析教材内容、课程标准，跳出具体的知识点，立足于可迁移的应用和持久的理解，设计出适合学生学习的目标，以便更好地落实学科核心素养，为开展教学活动提供可靠保障。

现以“平面向量”单元为例，以“平面向量”为主题，以“建立向量模型及简化可以用代数运算描述几何图形的规律”为单元大概念，制定单元的教学目标。在向量的学习之前，学生的数学知识系统中已经具有了学习向量的知识基础，学生能够对运算对象进行抽象与表示，掌握了数的运算体系的研究方法，具备了一些解决问题的能力。上述分析已经给出了“平面向量”单元的大任务：（1）了解向量是一种怎样的数学工具；（2）如何借助代数运算刻画几何图形？（3）建立向量模型并用向量模型解决几何问题。

基于对以上学习大任务的分析，将基于大概念的单元教学目标设计如下（见表1）。

表1 平面向量大单元学习目标

（三）制定基于大概念的评估依据

评估依据是逆向教学设计模式的重要环节，倾向于设置基于真实情境的表现性任务对学生学习的全过程进行评估，旨在引领学生学习的全过程。评估依据可以来自课堂的观察与对话、师生的交谈、随堂测试、作业、反思以及表现性任务。基于单元教学目标制定评估依据，评估学生是否达到了教学目标的预期结果，有利于发现问题并进行调整。具体的评估依据见表2。

表2 平面向量大单元的评估依据

（四）基于大概念的单元教学设计

围绕单元大概念创设问题情境，需要关联教学内容与学生的生活经验，让学生深入问题情境中，以核心问题为导向，以基本问题为探究线索，引导学生深度思考，帮助学生在已有的学习基础之上自主建构知识，落实学科核心素养。现以“平面向量”单元为例，以“建立向量模型及简化可以用代数运算描述几何图形的规律”为单元大概念，以“如何用向量模型解决问题？”为大任务，设置了三个问题情境，同时围绕大概念与单元教学目标设置与之相匹配的“核心问题”。具体如表3所示。

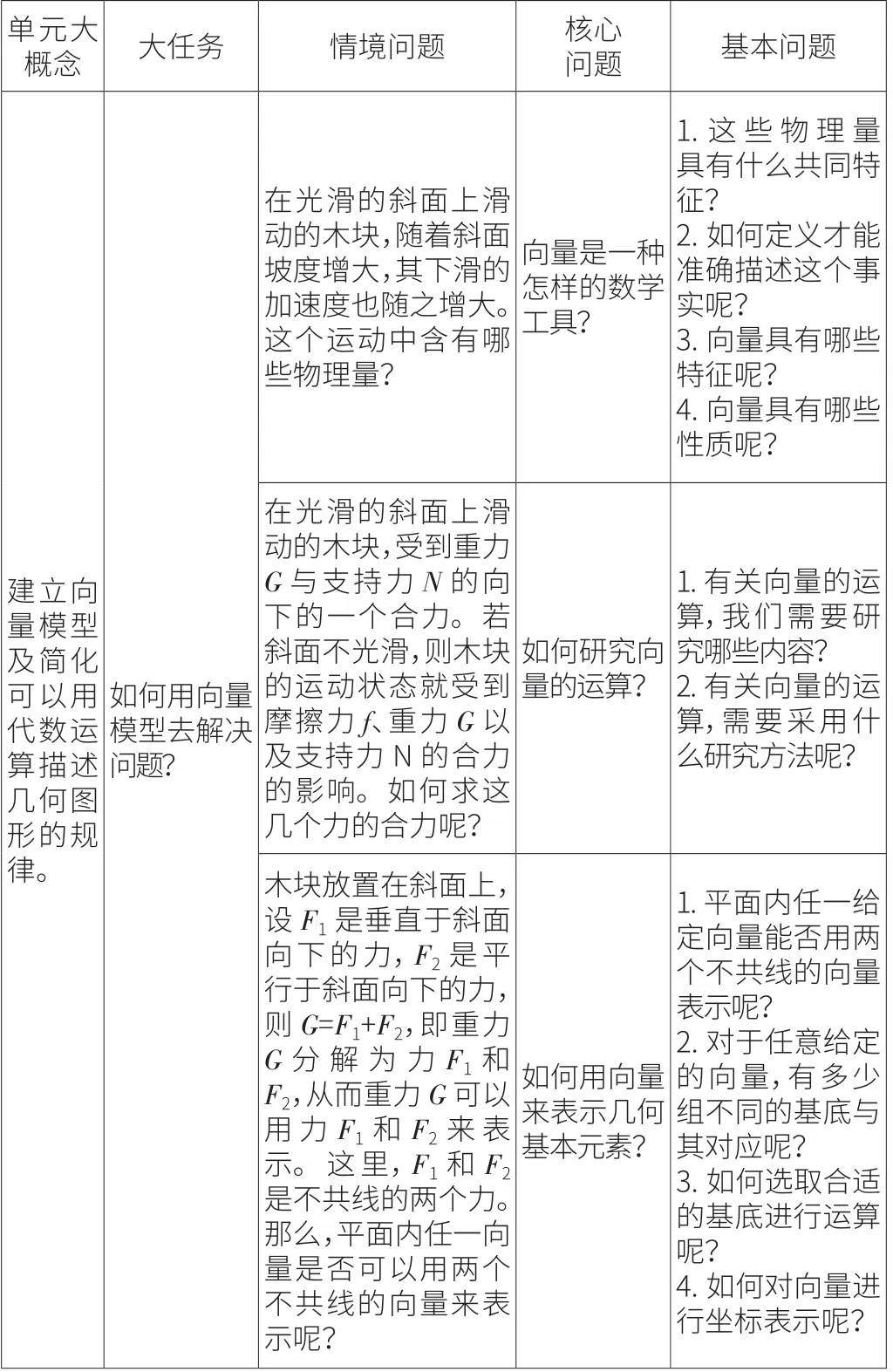
表3 基于大概念的单元情境与问题设计

学生通过探究和思考，很容易建构起向量的知识逻辑结构图（见图2），对向量的有关知识形成初步认识。

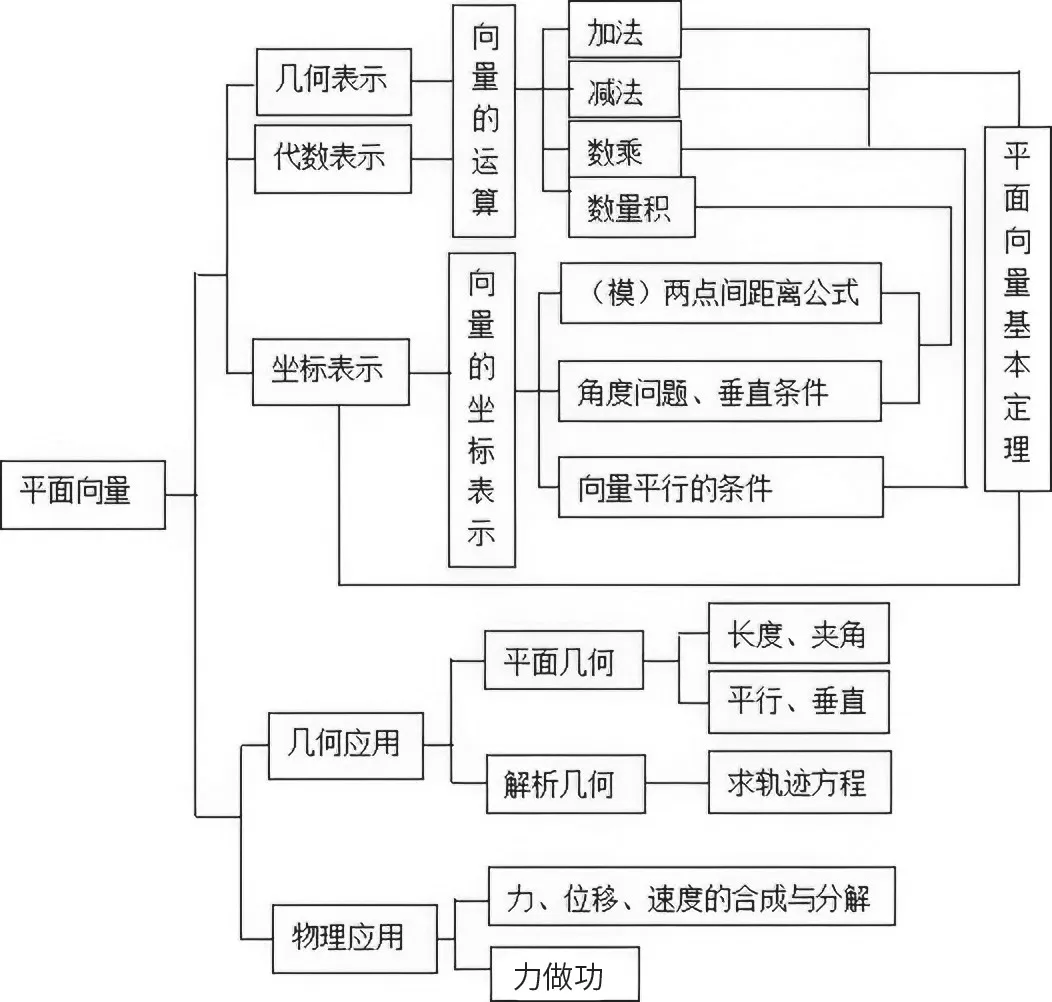
图2 “平面向量”单元知识的纵横关系

通过梳理单元知识之间的纵横关系，从具体小单元的知识出发，提炼出能够承载小单元的大任务，然后再进一步概括为更为上位的单元大概念，促使学生在不断的学习中构建出内涵丰富的知识框架。这种自下而上进行抽象概括的思路能够帮助我们找到具体知识之间的关联，为单元教学设计提供了新的思路。