排队系统中的顾客进队策略分析
韦骁劼
(广西职业师范学院,广西 南宁 530007)
1 排队论概述
一个排队系统由队伍与服务台构成,日常中可视为排队系统的现象有购物、餐厅等位、交通拥堵、医院救护、水库泄水、飞机起降的调度、码头货物的装卸、工厂的流水线生产、网络数据传输。当顾客在排队时,很自然想到的问题就是“我还需要等多久”“有多少人排在我前面”等等诸如此类的问题。而作为服务系统的管理者,虽然提高服务效率可以减少拥挤,然而过度的提升,会造成资源的浪费,也会加速服务设备的损耗,所以,管理者会很自然去关心如何合理的调整服务台的服务能力,使之既能满足顾客的需求,又能最大程度的节约运营成本。为了解决优化顾客与服务台之间的问题,便发展出了排队论这个领域,经过了一个世纪的发展,排队论的应用已经深入各个领域,在交通运输、仓库存储、工业生产、网络数据传输、计算机系统设计、自动化技术、可靠性理论甚至军事作战领域都能看到排队论的身影。
排队系统的相关研究最早是在20 世纪初由埃尔朗(A.K.Erlang,丹麦数学家)研究话务理论开始[1],他得出了著名的埃尔朗损失率公式并且为排队理论奠定了基础。20 世纪30 年代波拉切克(Pollacezk F,法国数学家)、辛钦(Khinchin A Y,前苏联数学家)等人也做了许多相关的工作,得到了一些重要的结果,比如波拉切克-辛钦公式。20世纪50年代,肯道尔(Kendall D G,英国数学家)使用嵌入马氏链方法进一步奠定了排队系统的理论基础,比如在M/G/1 与GI/M/1 排队系统中,嵌入点分别是顾客的离去时刻与到达时刻。除了嵌入马氏链方法,学者们还运用许多其他方法对排队系统进行研究,比如积分方程方法、补充变量法、向量马氏过程方法、矩阵几何方法。
在排队论中,最经典的模型是M/M/1 排队系统,学者们不仅研究了该系统的平稳性态,还得出了瞬时性态的结果。虽然泊松输入这个假设在实际情况中不一定能成立,比如去食堂吃饭的学生大都集中在下课之后,这就不满足平稳性的假设,又比如去食堂吃饭的学生往往是三两成群,这就不满足普通性的假设,还有就是如果某个学生觉得这个食堂的菜比较好吃,那么下次他极有可能再来这个食堂吃饭,这就不满足独立增量性这个假设。然而,泊松输入过程仍可以看成是实际情况相当程度上的近似。随着研究的深入,科学家们还考虑了其他情形更为一般排队模型,并且都得到了瞬时性态的相关结果。比如GI/M/1 型排队系统、离散时间排队系统、GI/M/n 型排队系统、GI/G/1型排队系统。
同时,还有许多具有特殊排队规则的排队系统也被科学家们深入的研究,比如带负顾客的排队系统、重试排队系统、带中途止步的排队系统、具有伯努利控制策略的排队系统。
对于一个排队系统,人们主要关心的性能指标是:
等待时间:指的是从顾客到达开始直到接受服务的这段时间。
逗留时间:指的是等待时间加上顾客被服务的时间,也就是从到达开始直到离开队伍的这段时间。
系统队长:指的是系统中的顾客数,包括正在排队的顾客和正在接受服务的顾客。
忙期:指的是从服务台开始工作直到把系统中的顾客全部服务完毕的这段时间。
闲期:指的是从服务台将顾客全部服务完毕开始直到下一次开始工作的这段时间。
忙循环:指的是相邻两次忙期的开始时间的间隔。
还有一个重要的指标是排队系统的服务强度,定义如下:
假设某个排队系统的顾客到达间隔的分布函数为A(x),服务时间的分布函数为B(x),记为公式(1)。

公式(2)称为服务台的服务强度。在许多排队系统中,ρ<1 是排队系统平稳的条件。
在经典排队系统中,服务台的服务率不会随时间变化,这明显与现实有着较大的偏差。比如生产工具的磨损会使生产效率降低,又比如由于交通拥堵导致路口的通过率下降。为此,研究者们在排队系统中引入了休假机制,这里的休假除了传统意义的“休假”外,也可以是在当前排队系统不繁忙时,服务台以较低的服务率来为顾客提供服务或者去从事另外一项服务工作,这被称为工作休假。
自从20 世纪70 年代,学者们首先对M/G/1 休假排队系统做了初步研究,此后休假排队系统立刻成为排队论的研究热点。库柏(Cooper R B)、哈里斯(Harris C M)等人利用随机分解手段并且做了大量的研究工作后,逐步完善了休假排队理论,田乃硕等首次利用矩阵几何方法来对休假排队系统研究,进一步推进了休假排队论的发展。直到2022 年,工作休假的概念才被提出,随后便引起了学者们的极大兴趣,大量关于工作休假排队系统研究工作就此展开。
与经典排队模型不同,在描述休假排队系统时,还要加入休假策略来进行描述。所谓休假策略,指的是触发休假的条件和休假结束的规则。一般来说,触发休假的条件有两类:第一类是当服务台忙期结束时立刻开始休假,被称为空竭服务;另一类是虽然系统中仍有顾客排队但也可以开始休假,被称为非空竭服务[2]。而常见的休假结束的条件有:
N 策略:当系统中排队顾客数到达指定数量N 时,服务台休假结束。
启动时间:当有新顾客到达系统时,服务台需要经历一个随机时长的启动期。
单重休假:服务台只进行一次休假,若休假结束时有顾客到达系统,则正常为顾客提供服务,若休假结束时仍无顾客到达,则进入闲期。
多重休假:服务台可进行多次休假,具体地说,若一次休假结束时系统中仍无顾客到达,则开始另一次独立同分布的休假,直到某次休假结束时系统中已有顾客在等待。
此外,还有许多休假策略的组合所形成的策略,比如N 策略多重休假,启动期单重休假等。
2 排队经济学概述
当顾客到达某排队系统时,根据队伍长度信息与服务台状态信息的不同组合,可将系统的信息水平分为四类:完全可见、几乎可见、几乎不可见以及完全不可见。排队经济学主要的研究目的是利用排队系统的相关指标来构建顾客和社会的收益函数,在考虑队伍长度以及服务台状态的前提下给出顾客的均衡进队策略和使得顾客和服务商的总收益达到最大的策略,即社会最优策略(顾客与服务商之间的利益转换不计入其中)。
在经典的排队理论中,顾客是被动接受服务的一方,无法主动做出决策。然而事实上,顾客会根据风险偏好、收支结构等因素,在处于不同的信息程度的条件下来做出自己满意的选择,最常见的就是顾客会考虑何时选择止步或者进队或者中途退出。而对于服务系统的管理者而言,由于提供服务的成本,他们需要控制客流量或者对顾客收取一定的费用。总之,顾客和管理者在决策的同时都必须把对方的行为考虑进去,于是就形成了双方的博弈。同样的,顾客与顾客之间也存在着博弈,比如排位靠前的顾客所做的决策可能会对后到的顾客产生影响。于是,越来越多的学者开始运用博弈论对于有顾客个体特征的排队系统进行研究。
最早的一篇基于博弈论的排队经济学文献是Naor[3]关于M/M/1 排队经济学模型的研究,并给出了在队伍长度及服务台状态可见时的顾客进队策略和社会最优策略,并且发现顾客为了追求个人最优,会对系统造成拥堵,于是提出需要对顾客征收一定的费用来保证社会收益最大化。而后侯赛因、拉森及内勒巴夫等学者对该模型进行了一系列的拓展。斯迪达姆研究了更一般的GI/M/1 排队模型,值得一提的是在大部分文献中,顾客经过服务后所获得的回报一般假设为常数R,而在斯迪达姆的文献中,顾客经过服务所获得的回报被假设为一个随机变量,同样的假设出现在米勒和巴克曼的文献中。除了上述经典排队模型,具有特殊排队规则的排队模型也被深入的研究。比如可修排队系统、有优先权的排队系统、重试排队系统。
2007 年学者们开始对休假排队系统中的排队经济学问题进行研究,博内塔斯与伊科诺穆在M/M/1 模型中加入了启动机制,并得出了在不同信息下的顾客进队策略,田乃硕、郭鹏飞等对该模型进行了推广,加入了启动可中断的条件。随后又有学者们提出了新的模型,他们引入了N 策略机制,即当系统中有N 名顾客排队时服务台便结束休假,同样得出了不同信息水平下的顾客进队策略,伊科诺穆、戈麦斯和坎塔考虑了M/G/1 多重休假排队系统,得出了在队伍长度不可知时的顾客进队策略和社会最优策略。另外,对于工作休假排队经济学模型的研究,成果如下:在单重工作休假的Geo/Geo/1 模型下,得出了在队伍长度及服务台状态都可知与都不可知情形下的顾客进队策略;更进一步地,考虑在服务完工作休假期中进入的第一名顾客后,如果仍有顾客在排队,则以某个正概率中断工作休假;如果没有顾客在排队,则继续工作休假的在休假可中断的Geo/Geo/1 工作休假模型下,得出了队长与服务台均可知、队长可知但服务台状态不可知与队长及服务台状态均不可知情形下的顾客进队策略与社会最优策略;在多重工作休假的M/M/1 排队模型中,给出了所有信息水平下的顾客进队策略与社会最优策略。在批量到达的GI/M/1 单重和多重休假排队系统中,分析了队伍长度与服务台状态均可见与队伍长度不可知但服务台状态可知下的顾客进队策略以及队伍长度及服务台状态均不可知情形下的社会最优策略。
3 一类排队系统中顾客的进队策略
考虑一个M/M/1 排队系统,并在该排队模型中加入启动机制及N 策略,即当系统中无人排队时,服务台开始休假期,不再提供服务,直到系统中有N 名顾客时时,服务台开始进入一个时长服从指数分布的启动期[4]。随后服务台开始工作直到系统再次变空。引入启动机制与N 策略具有很现实的应用背景,比如当水位到达一定高度时,水库才开始开闸泄洪,又比如大巴车需要等到满座才发车。进一步地,假设每名顾客都是风险中立的,并且顾客一旦选择进队就不允许退出,而选择止步的顾客则不允许再次进入队伍。顾客在被服务完毕后可获得的回报为常数R,逗留期间每个单位时间的等待费用为常数C。同时,为使系统为空时顾客选择进队,应有回报R 大于该顾客的总等待费用。
先考虑在完全可见情形下的顾客进队策略,此时顾客知道排队人数以及服务台处于休假期、启动期还是正在工作。作为顾客而言,一个最直观的想法就是根据排队人数来决定是否进入队伍,因此可以选择阈值策略,即顾客根据服务台的不同状态来选择进入队伍的不同阈值。顾客发现服务台在休假且有n 人排队,若n<n_0,则选择进队,否则止步;顾客发现服务台在启动且有人排队,若n<n_1,则选择进队,否则止步;顾客发现系统在工作且有n 人排队,若n<n_2,则选择进队,否则止步。显然,在服务台休假时到达的顾客必然会选择进入队伍。而对于处于启动期与工作期的排队系统,根据阈值策略可求得:
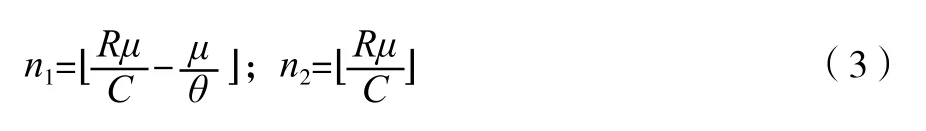
根据以上分析有如下结论:在完全可见情形下,策略“若顾客发现系统在休假则必然进队;顾客发现系统在启动期且排队人数少于则选择进队,否则止步;顾客发现系统在工作且排队人数少于则进队,否则止步”唯一的均衡策略。
接下来进一步地考虑在几乎可见情形下的顾客进队策略,此时顾客知道排队人数但不知道服务台处于休假期、启动期还是正在工作,与完全可见情形完全类似,顾客很自然地会根据队伍人数来选择是否进队,因此仍然考虑选择阈值策略,即:顾客发现系统中有n人排队,若n<ne,则选择进队,否则止步。此时,可列出平衡方程,进而得出系统的稳态概率。更进一步的,由稳态概率可列出关于收益的函数,经过一系列分析可得出结论:在几乎可见情形下,对于具有启动期及N策略的M/M/1 排队系统,存在正整数K1、K2(K1<K2)使得进队阈值ne∈[K1,K2],并且策略“若排队人数n<ne,则顾客进队;否则,顾客止步”是均衡策略。[5]
在R=25,C=1,N=5,λ=0.5,μ=1,θ=0.1 时的系统收益函数图像,经过计算可知K1=16,K2=19。这就是说对于该排队系统而言,当队伍长度为16 至19人时,均可选择进队,但是当队伍长度至少为20 人时,就应该止步。

