基于改进粒子群算法的电力系统储能容量配置方法

赵 扉，薛龙江，朱晶亮，陈鼎，方景辉，吴军，朱悦人

（1.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314033；2.国网浙江省电力有限公司平湖市供电公司，浙江 嘉兴 314000）

0 引言

电力系统储能容量的调节和调度过程受到应用场景、容量、经济成本等多种因素的影响，如何对电力系统储能容量进行最优配置，是现今电力系统发展亟待解决的问题之一。

文献［1］建立了考虑风电不确定性、风电爬坡和风电消纳问题的多参数储能配置模型，基于单一变量原则和相关性分析，量化研究系统中各类参数对储能配置的影响，但未考虑可靠性约束，导致配置成本较高。文献［2］研究了考虑风电不确定性和弃风率约束的风电场储能容量配置问题，根据历史数据构造风电出力的经验分布函数，建立以储能投资成本最小为目标、以弃风率为约束的鲁棒机会约束规划模型，将鲁棒机会约束转化为传统机会约束，并采用凸近似和抽样平均构建线性规划进行高效求解，但未考虑配置场景条件，导致配置效率较低。文献［3］分析了各种储能技术在响应特性、经济成本、容量规模等方面的特点，针对提高能耗和调峰压力的技术瓶颈，提出一种由全钒液流电池和先进绝热压缩空气储能组成的混合储能系统，在此基础上建立一种新的两级容量优化分配的电力资源混合储能系统模式，上层以综合投资最小为指标，下层以系统运行费用最小为指标，确定其调度能力，不仅能满足电力市场各种特性的要求，而且能提高电力市场的经济效益。

以上研究方法未考虑可靠性约束、配置场景条件等问题，使得储能容量配置成本较高、配置效率较低，无法满足电力系统的发展需求。为了提高配置效率，降低配置成本，本文提出基于改进粒子群算法的电力系统储能容量配置方法。创新性地在储能系统剩余电量、充/放电功率、可靠性3个方面进行相应的约束，根据负荷缺电率与电力系统光伏发电成本设置储能容量配置目标函数；采用量子力学中的波函数改进粒子群算法，计算电力系统储能配置功率，进而确定电力系统储能配置容量，以提高储能容量配置寻优的速度，缩短电力系统储能容量配置时间，优化储能容量净收益数值模拟过程，提升储能容量配置性能。

1 电力系统储能容量配置方法

1.1 电力系统储能容量确定

电力系统储能容量确定是储能容量配置的首要环节，也是储能容量配置的基础与前提［4］。以光伏与风力发电作为电力系统储能的主要形式，储能容量确定步骤如下。

步骤1，获取电力系统储能容量相关数据。针对某个研究区域，在电力系统中导出历史数据信息，获取时刻t对应的电力系统功率数据，表达式为：

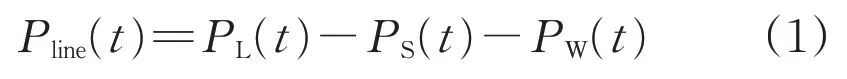
式中：Pline(t)为时刻t电力系统功率；PL(t)为时刻t采样负荷；PS(t)为时刻t光伏出力；PW(t)为时刻t风电出力。Pline(t)＞0 时，表明功率从主电网流向区域电网；Pline(t)＜0时，表明功率从区域电网流向主电网［5］。

步骤2，分析电力系统功率数据。对步骤1得到的电力系统功率数据Pline(t)进行频谱分析，表达式为：

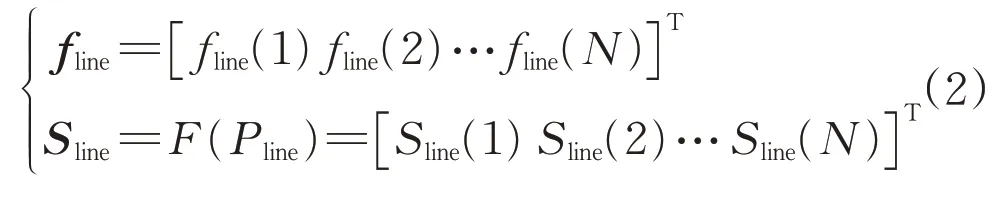
式中：fline为功率数据Pline(t)的傅里叶变换结果；Sline为其对应的分量；N为功率数据总数；F(Pline)为样本数据的傅里叶变换函数。

步骤3，计算电力系统储能配置功率。采用平滑功率目标输出的形式，表示电力系统储能配置理想功率输出结果，表达式为：

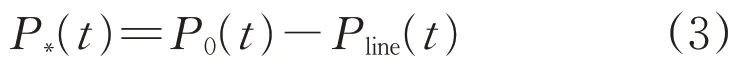
式中：P*(t)为电力系统储能配置理想功率输出；P0(t)为平滑功率目标输出。P*(t)＞0时，表明储能系统处于放电状态；P*(t)＜0 时，表明储能系统处于充电状态［6］。

步骤4，确定电力系统储能配置容量。实际电力系统运行过程中，储能设备在充/放电转换过程中会存在一定的损耗。以步骤3 计算结果为依据，累计全部采样时刻的储能充/放电电量，即可获得电力系统储能配置容量［7］，计算公式为：

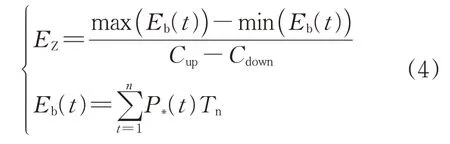
式中：EZ为电力系统储能配置容量；Eb(t)为时刻t储能系统相对于初始状态的容量波动；Cup和Cdown分别为储能系统运行过程中的荷电上限约束和下限约束；Tn为储能容量数据的采样周期；n为采样点数。

1.2 储能容量配置约束条件分析

储能容量配置需要满足多种约束条件，这是储能容量配置优化的关键。本文借鉴已有文献研究成果［8］，对储能系统剩余电量、充/放电功率、可靠性进行相应的约束。

储能系统剩余电量也被称为SOC（荷电状态），一直处于动态变化中，由充/放电功率、效率等因素决定。剩余电量需要满足下述约束条件：

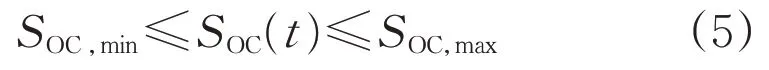
式中：SOC(t)为时刻t储能系统SOC；SOC，min和SOC，max分别为储能系统SOC的最小值和最大值。

储能系统充/放电功率计算公式为：

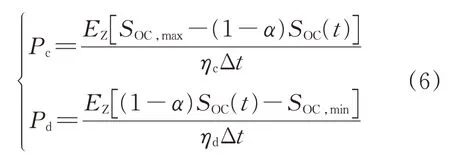
式中：Pc和Pd分别为充电功率和放电功率；α为功率计算辅助因子，取值范围为[0，1]；Δt为采样时间间隔；ηc和ηd分别为充电功率和放电功率的误差参量，取值范围需要根据实际情况进行设置。

储能系统充/放电功率约束条件为：

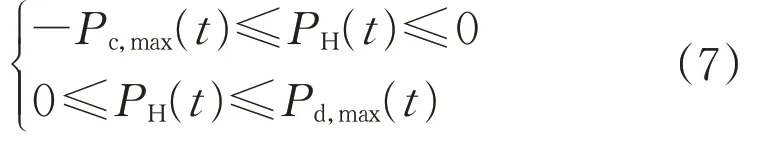
式中：Pc，max(t)和Pd，max(t)分别为充电功率和放电功率的最大值；PH(t)为时刻t的充/放电功率实际数值。

可靠性约束主要依靠负荷缺电率来衡量，计算公式与约束条件为：

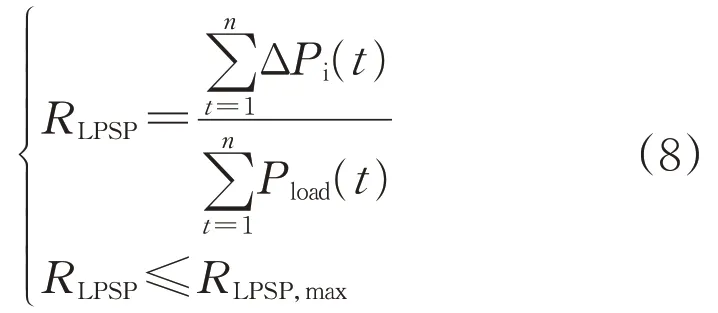
式中：RLPSP为负荷缺电率；ΔPi(t)为时刻t的缺电功率；Pload(t)为负荷总需求功率；RLPSP，max为负荷缺电率的最大值。

1.3 电力系统经济模型

依据1.1 节和1.2 节确定的储能容量与约束条件，基于成本理论以净收益最大为储能容量配置目标，构建电力系统经济模型（即储能容量配置目标函数），表达式为：

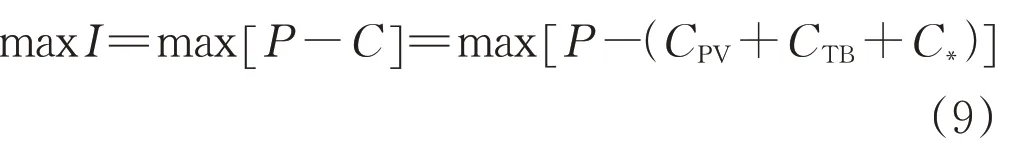
式中：I为收入；P为支出；C为成本；CPV为光伏发电成本；CTB为风力发电成本；C*为电力系统储能容量配置的其他成本。

电力系统光伏发电成本CPV主要由运行成本及其折旧成本决定，计算公式为：

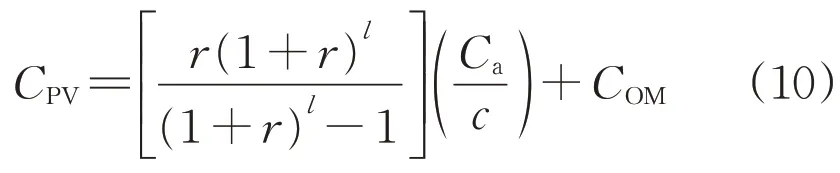
式中：r为固定年利率；l为运行年数；Ca为光伏发电装机成本；c为平均容量系数；COM为光伏发电运行成本。

1.4 基于改进粒子群算法的储能容量配置

引入改进粒子群算法求解1.3节构建的电力系统经济模型，算法输出结果即为最优电力系统储能容量配置结果。一般粒子群算法的粒子搜索速度较慢，改进粒子群算法主要采用量子力学中的波函数描述粒子的速度与搜索位置，提高粒子搜索速度，以实现储能容量快速配置。另外，粒子群算法容易陷入局部寻优状况，导致搜索精准度较差，本文以变异操作改进粒子群算法，使粒子持续进行迭代运算，提高搜索精准度。

设定改进粒子群算法搜索空间由目标函数所有解构成，记为集合X，集合中移动粒子的数量采用波函数ψ(t)表示，t∈X。选择p点作为搜索空间的中心［9-11］，随着时间的推移，粒子逐渐接近p点。粒子运动方程为：

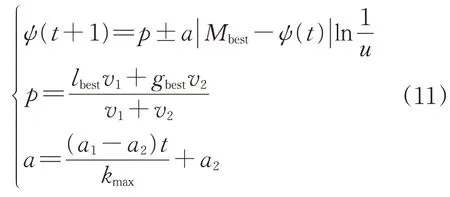
式中：ψ(t)为时刻t移动粒子的数量；a为变收缩因子；Mbest为种群中粒子的总数量［12-14］；u为服从泊松分布的任意整数值；lbest和gbest分别为局部最优值与全局最优值；v1和v2为粒子运行速度参量，取值范围为[0，1]；a1和a2分别为变收缩因子的开始值和结束值；kmax为改进粒子群算法的最大迭代次数。

为了防止算法进入局部寻优状况，设定多样性度量值ω0。若种群多样性大于ω0，正常进行算法流程；若种群多样性小于ω0，需要对种群粒子进行变异操作。变异公式为：

式中：ε为变异因子。

以变异操作后的粒子继续进行迭代运算，直至满足最大迭代次数条件为止，输出结果即为最优电力系统储能容量配置结果。

通过上述过程，应用改进粒子群算法实现了电力系统储能容量的配置，加快了储能容量配置寻优的速度，可为电力系统稳定运行提供保障。

2 实验与结果分析

2.1 实验对象

为了验证本文提出方法的应用性能，选取文献［1］方法和文献［2］方法分别作为对比方法1和对比方法2，设计对比实验。选取某地区电力系统随机10 日（工况序号1—10）的储能数据作为实验对象，并对储能设备进行选取和配置。

实验对象储能数据如图1所示。

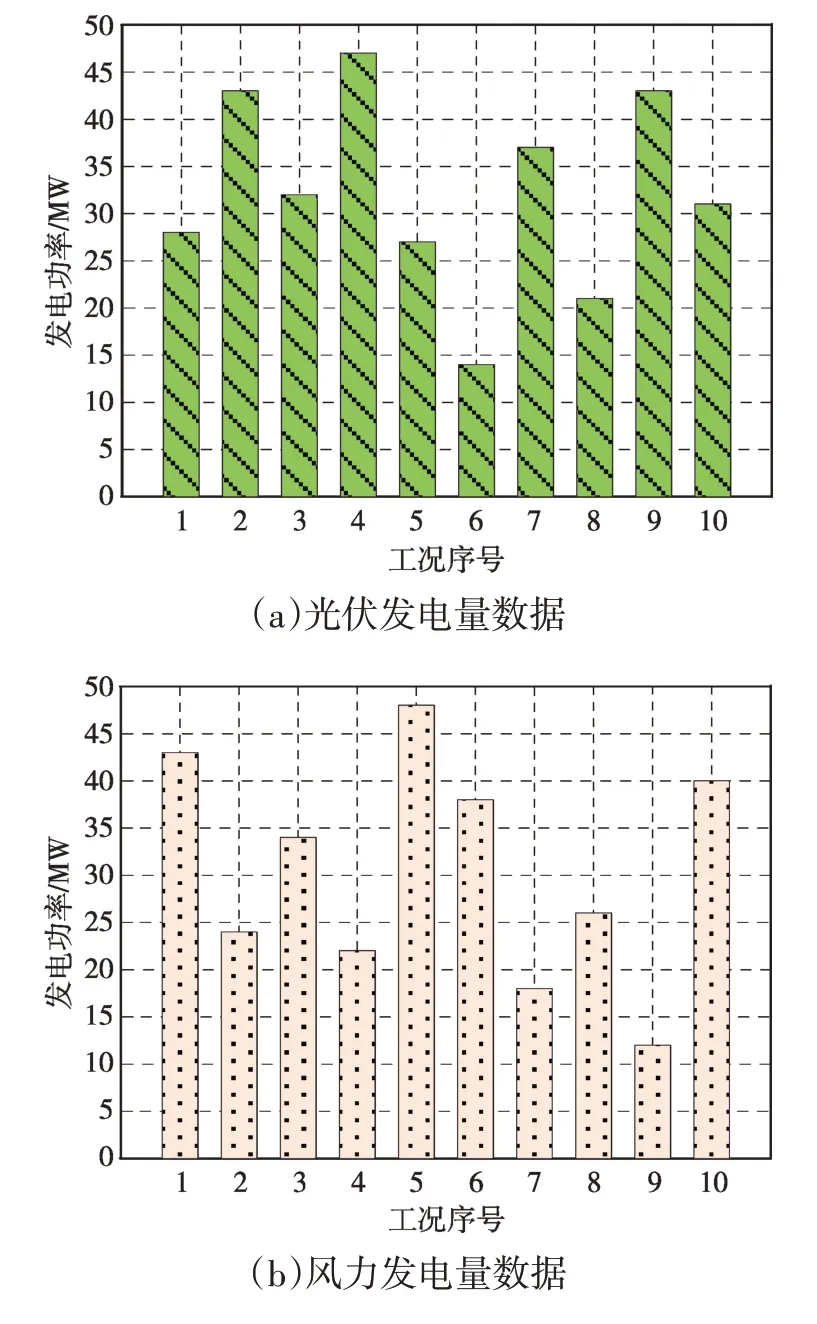
图1 实验对象储能数据

实验对象采用超级电容与蓄电池作为电力系统储能设备，依据储能容量配置需求，对储能设备参数进行合理设置，如表1所示。

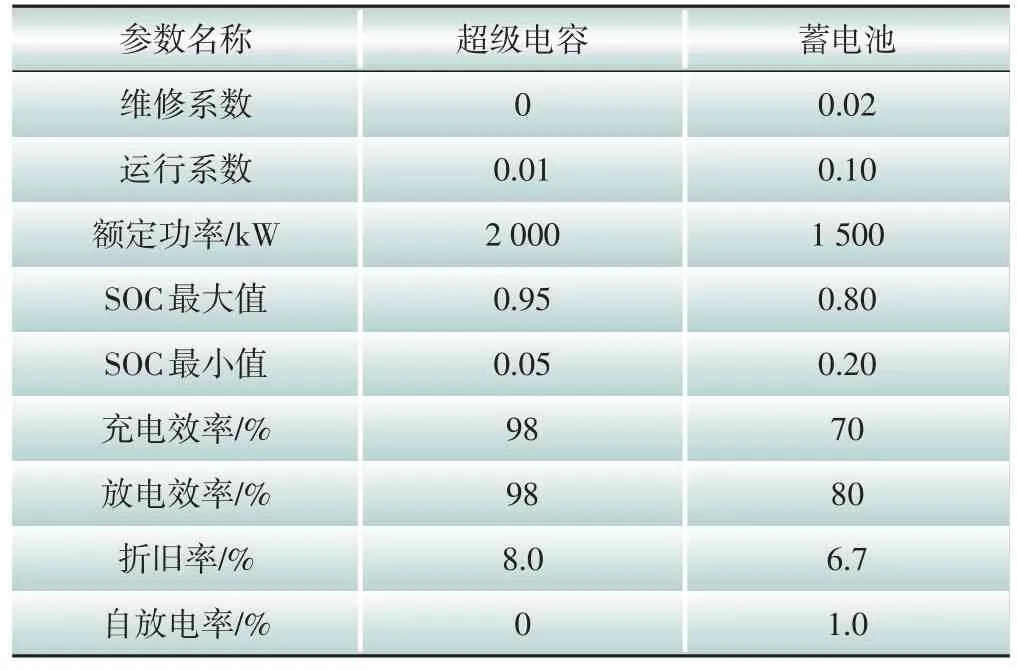
表1 储能设备参数设置

2.2 实验结果分析

以上述选取的实验对象、获取的实验数据、设置的储能设备参数为基础，进行电力系统储能容量配置实验。为了客观表示储能容量配置性能，选取储能容量配置时间与储能容量配置净收益作为评价指标，具体实验结果分析如下。

2.2.1 储能容量配置时间分析

储能容量配置时间直接反映电力系统储能容量配置方法的效率，一般情况下：储能容量配置时间越短，表明方法应用效率越高；储能容量配置时间越长，表明方法应用效率越低。通过实验获得7 日（工况序号1—7）的储能容量配置时间数据，如图2所示。

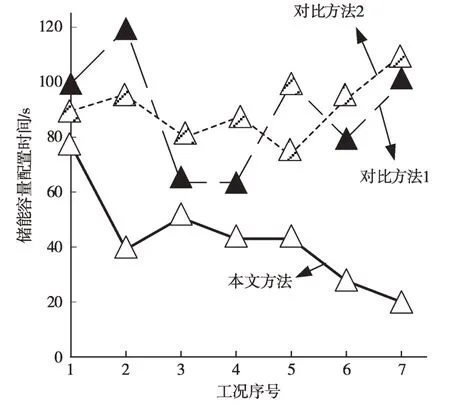
图2 储能容量配置时间数据

由图2可以看出，相对于两种对比方法，本文方法的储能容量配置时间更短，储能容量配置效率更高。本文方法取得优势结果的原因是，改进粒子群算法主要采用量子力学中的波函数描述粒子的速度与搜索位置，加快了粒子搜索速度，为储能容量配置的快速实现提供了助力。

2.2.2 储能容量配置净收益分析

储能容量配置净收益直接反映电力系统储能容量配置方法的效果，一般情况下：储能容量配置净收益数值越大，表明储能容量配置效果越好；储能容量配置净收益数值越小，表明储能容量配置效果越差。通过实验获得储能容量配置净收益数据，如图3所示。

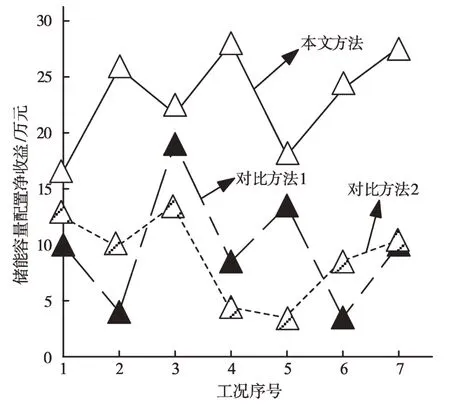
图3 储能容量配置净收益数据

由图3可以看出，应用本文方法获得的储能容量净收益数值最高值达到28万元，工况2、4、6、7的收益情况较对比方法有明显提高。以上数据充分表明本文方法能够带来巨大的收益增长，具有优秀的应用前景。

2.2.3 储能容量配置可靠性分析

不同应用场景的电力系统波动率对储能容量的配置有很大影响，因此，测试不同功率波动对3 种储能容量配置方式的影响程度，以验证本文配置方法的可靠性。3种方法的可靠性测试结果如图4所示。

图4 可靠性测试结果

由图4可以看出，随着限制波动率增大，能够配置的储能最大容量相应减小。本文方法的配置储能变化较为平稳，可配置容量保持在20 MWh以上，而其他方法的可配置容量降低到10 MWh以下，证明本文方法受电力系统功率波动影响程度较低，可靠性较高。这是因为本文考虑了可靠性约束、配置场景条件等，提高了配置可靠性。

3 结语

本文引入改进粒子群算法，设计了新的电力系统储能容量配置方法。采集电力系统储能容量相关数据，分析并计算电力系统储能配置功率；累计全部时刻的储能充/放电电量，确定电力系统储能配置容量；在储能系统剩余电量、充/放电功率、可靠性3个方面进行了相应的约束，根据负荷缺电率与电力系统光伏发电成本设置储能容量配置目标函数；应用波函数描述粒子的速度与搜索位置，对粒子群算法进行改进。实验结果表明该方法加快了储能容量配置寻优的速度，极大地缩短了储能容量配置时间，提高了储能容量净收益，可以为储能容量配置提供更有效的方法支撑，也为电力系统的发展提供助力，为居民、企业等电力用户提供更加优质和稳定的电力供应。

本文未考虑各个分区的负荷水平和设置备用需求系数，存在模型响应特性不明显的问题。在未来的研究中，应根据区域调频需求，分析惯性响应能力，进一步优化电力系统储能容量配置结果。