汽车转向非线性平衡点求解新方法及其应用

李杰，贾长旺，赵旗

（吉林大学汽车仿真与控制国家重点实验室，长春 130025）

传统的汽车理论是采用线性轮胎模型进行汽车性能研究的，经典的汽车操纵稳定性理论也是在此基础上发展起来的［1］。然而，轮胎非线性对汽车性能的影响很大，在高速或大转角行驶条件下，轮胎很容易进入非线性区域，如果再使用线性轮胎模型进行汽车性能研究，会造成较大的误差［2］。

转向非线性平衡点是进行汽车转向非线性稳定性分析与控制的起点，只有在确定转向非线性平衡点后才能判别汽车转向非线性运动稳定性。稳定的转向非线性平衡点决定了汽车非线性转向运动的稳定性，不稳定的非线性转向平衡点表征了汽车非线性转向稳定域的边界，由此划分出汽车转向非线性运动的稳定域和非稳定域［3］，便于分析和应用。通过将转向非线性平衡点作为稳定域边界，可用双直线［4］或菱形［5-7］等描述汽车非线性运动的稳定域，以此实现汽车转向非线性稳定性控制系统设计［8-9］。此外，非线性分岔可能会在转向非线性平衡点处发生［10-13］。一旦发生分岔，汽车很有可能会变得不稳定［14-15］。因此，针对不同行驶条件，定量确定转向非线性平衡点及其变化规律，对汽车非线性转向稳定性分析与控制的研究具有重要意义。

以往求解转向非线性平衡点，最常用的方法是通过在相平面或者相空间中绘制相轨迹获得［3-6］，优点是清晰直观。然而，这种图解法的缺点是只能确定转向非线性平衡点的大概位置；并且对于转向非线性平衡点的连续求解和复杂汽车模型的转向非线性平衡点求解，这种图解法也是有一定难度的。

为了克服转向非线性平衡点求解图解法的缺点，提出了求解转向非线性平衡点的常规数值方法和遗传算法［16］。常规数值方法多采用梯度类算法求解转向非线性平衡点，如下降法、牛顿法或拟牛顿法等，存在初值敏感性问题，即对初值比较依赖，没有较好的初值，往往得到较好的结果。遗传算法是一种智能算法，具有较强的全局寻优能力，不依赖初值，已经用于转向非线性平衡点的求解，但是遗传算法存在早熟、停滞、重复等问题，造成过多的迭代。为克服遗传算法存在的问题，提出了将遗传算法与拟牛顿法相结合求解转向非线性平衡点的混合优化算法［17］，取得了不错的效果。但是算法复杂，耗时较长，在求解转向非线性平衡点时，会耗费很多时间。因此，需要对转向非线性平衡点的求解进行更多的研究，找到一些更加简单和快速求解转向非线性平衡点的方法，以便更好地开展汽车转向非线性稳定性分析与控制的相关研究。

针对转向非线性平衡点求解问题，在前人研究的基础上，结合汽车转向非线性2自由度模型，提出求解转向非线性平衡点的粒子群算法，对转角、路面附着系数和车速分别变化行驶条件的转向非线性平衡点进行求解。

1 汽车转向非线性2自由度模型

1.1 汽车模型

汽车转向2自由度模型是最经典的操纵稳定性模型，可以揭示汽车的基本规律，应用广泛［1］。因此，选择汽车转向2自由度模型为研究对象。考虑汽车的侧向运动和横摆运动两个自由度，模型的微分方程表示为：

式中：m为汽车总质量；Iz为横摆转动惯量；a为汽车质心到前轮的距离；b为汽车质心到后轮的距离；ay为汽车质心侧向加速度；γ为汽车质心横摆角速度；Fyf为前轴轮胎侧向力；Fyr为后轴轮胎侧向力。

汽车质心侧向加速度的计算公式为：

式中：u为汽车纵向速度，假设为常速；β为汽车质心侧偏角。

将式（3）代入式（1），有：

联立式（4）和式（2）进行变换，得：

取状态变量x=[β，γ]T，将式（5）和式（6）改写成状态方程，有：

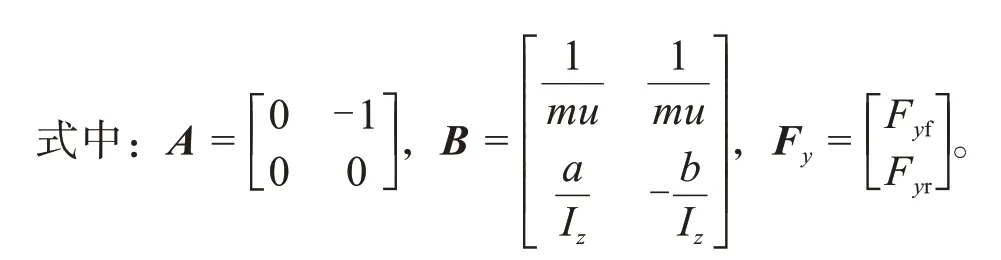
1.2 非线性轮胎模型

采用简化魔术公式轮胎模型描述轮胎侧向力，公式为：

式中：μ为路面附着系数；Fz为车轮垂向载荷；α为轮胎侧偏角；C和B为魔术轮胎模型参数。

将式（8）应用于前后轮胎时，需要确定前后轮垂向载荷和前后轮胎侧偏角。前后轮垂向载荷计算公式为：

式中：Fzf为前轮垂向载荷；Fzr为后轮垂向载荷；g为重力加速度。

前后轮胎侧偏角计算公式为

式中：αf为前轮胎侧偏角；αr为后轮胎侧偏角；δ为前轮转角。

2 汽车转向非线性平衡点求解

2.1 转向非线性平衡点

式（8）的非线性导致Fy非线性，因此，式（7）就成为非线性方程，可表示为非线性自治系统的形式：

满足̇=0，即同时满足̇=f1(β，γ)=0和γ̇=f2(β，γ)=0的点xe=[βe，γe]T，称为汽车转向非线性平衡点，简称为转向平衡点。

2.2 粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）是模拟鸟群觅食行为而提出的一种优化算法。鸟群在搜索食物时，会相互交换信息，每只鸟根据自身信息与其他鸟信息，再根据自己与食物的距离对搜索方向做出调整。在距离食物最近的鸟的周围区域搜索可以更快找到食物，通过鸟之间的合作可以使鸟群最快搜索到食物［18］。

在PSO中，将优化问题的解看作是搜索空间中的一只鸟，称为“粒子”，将鸟群作为“群体”。每个粒子具有和鸟类捕食类似的行为规则，从搜索空间的随机解出发，通过逐步迭代搜索问题的最优解。在每一步迭代中，粒子根据本身的最优解和整个群体的最优解来调整自己的速度，群体更新当前最优解，从而使个体和群体逐步优化。

下面对粒子群算法的实现过程进行描述。假设在一个D维的搜索空间中，有N个粒子组成一个群体。对于i=1，2，…，N，第i个粒子的位置表示为一个D维向量：

第i个粒子的速度也是一个D维向量：

第i个粒子迄今为止搜索到的最优位置称为个体极值，记为：

迄今为止，整个粒子群搜索到的最优位置为全局极值，记为：

在每一步的迭代中，粒子根据如下公式来更新自己的速度和位置：

式中：w为惯性权重；c1和c2为学习因子；r1和r2为［0，1］范围内的均匀随机数。

粒子群算法流程，如图1所示。为了实现粒子群算法，首先，要根据具体问题，设计适应度函数fitness，用于计算适应度；其次，设置基本参数，包括维数D、粒子数目N、惯性权重w、学习因子c1和c2、最大迭代数M、精度ε；再次，设置粒子群初始的位置和速度，既可以设置为随机值，也可以根据求解的问题设置相应范围；最后，设置迭代终止条件，让迭代次数k达到最大迭代次数M或者适应度fitness满足精度要求ε，即：

图1 粒子群算法流程

2.3 转向平衡点求解的粒子群算法

为了应用粒子群算法求解转向平衡点，需要设计适应度函数fitness。转向平衡点求解问题，就是找出̇=f1(β，γ)=0和̇=f2(β，γ)=0的解，可以将其转换为求解适应度函数最小值的数学问题，即：

求解转向平衡点的粒子群算法，步骤具体如下：

（1）设置粒子群算法基本参数：维数D、粒子数目N、惯性权重w、学习因子c1和c2、最大迭代数M、精度ε。

（2）确定粒子群位置范围(βmin，βmax)、(γmin，γmax)和速度范围[-vβm，vβm]、[-vγm，vγm]。

（3）在粒子群位置范围和速度范围内，生成均匀分布的每个粒子的位置初值βi、γi和速度初值vβi、vγi，i=1，2，…，N。

（4）由式（21）计算每个粒子的适应度fitness。

（5）通过逐步比较，获得每个粒子的个体最优位置βibest、γibest，通过整个种群比较，获得群体最优位置βbest、γbest。

（6）检查是否满足终止条件，即式（20），如果满足，结束搜索，输出当前群体最优值βbest、γbest；如果不满足，转向步骤（7）。

（7）迭代更新第k+1步的粒子速度：首先，按照式（18）初步更新每个粒子速度，得到v′βi、v′γi；其次，要保证速度在限制范围内，因此，第k+1步迭代的粒子速度为：

（8）迭代更新第k+1步的粒子位置：首先，按照式（19）初步计算每个粒子位置，得到β′i、γ′i；其次，保证粒子位置在限制范围内，当β′i>βmax时，将β′i依次减去βmax-βmin，直到βi′∈[βmin，βmax]；当β′i<βmin时，将 β′i依 次 加 上 βmax-βmin，直 到β′i∈[βmin，βmax]；粒子位置βik+1为处理后的β′i，按照同样的方法得到γki+1。

（9）转入步骤（4）。

需要指出的是，粒子群算法是一种启发式算法，具有随机性，一次求出的结果不一定都能满足精度要求。当结果不满足精度要求时，通过多次运行程序求解或者改变群初值和求解范围，问题就会得到解决。

3 应用分析

3.1 参数设置

设置汽车和轮胎参数，见表1；设置粒子群算法参数，见表2。

表1 汽车参数

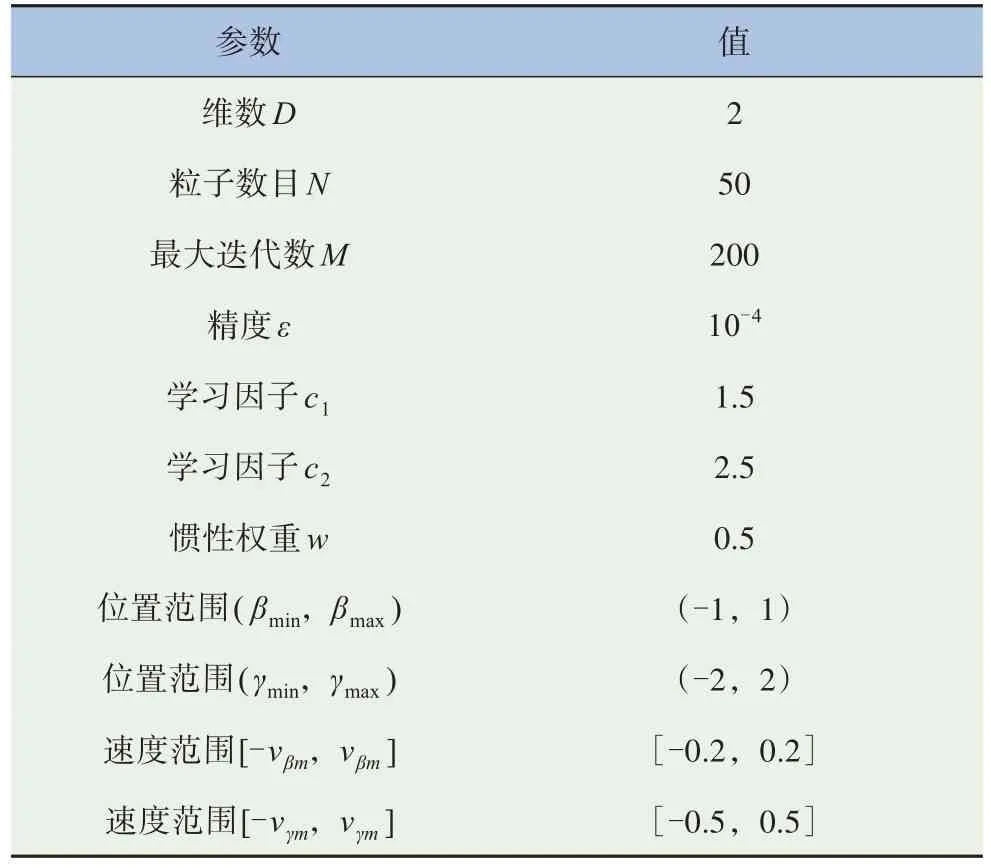
表2 粒子群算法参数

3.2 不同转角下转向平衡点求解

选择路面为良好路面，路面附着系数μ设置为0.8，车速u设置为70 km/h，汽车左转和右转情况相同，因此，只需要研究前轮转角δ为正值的情况，范围取为0～0.2 rad，以0.02 rad为间隔。

求解得到的3个转向平衡点，如表3～5所示。由这些表可以看出，应用粒子群算法求解的转向平衡点都能满足设置的精度要求；在某一固定转角下，一共有3个转向平衡点；随着前轮转角增大，第1个转向平衡点和第3个转向平衡点的β值增大，γ值变化不大；第2个平衡点的β值减小，γ值增大。

表3 u=70 km/h和μ=0.8时的第1个转向平衡点

表4 u=70 km/h和μ=0.8时的第2个转向平衡点

3.3 不同路面附着系数下转向平衡点求解

选择从结冰路面到良好路面，路面附着系数μ范围取0.2～1，以0.1为间隔。考虑到在结冰路面上汽车都会减速慢行，设置车速u为30 km/h，前轮转角δ为0.1 rad。

求取的转向平衡点，如表6～8所示。由这些表可以看出，应用粒子群算法求解的平衡点都能满足设置的精度要求；在某一固定路面附着系数下，一共有3个转向平衡点；随着路面附着系数的增大，第1个转向平衡点β值增大，γ值减小；第2个转向平衡点的β值增大，γ值增大；第3个转向平衡点β值增大，γ值减小。

表6 u=30 km/h和δ=0.1 rad时的第1个转向平衡点

3.4 不同车速下转向平衡点求解

选择路面为良好路面，路面附着系数μ设置为0.8，车速u的范围取30～120 km/h，以10 km/h为间隔，前轮转角δ为0.1 rad。

表5 u=70 km/h和μ=0.8时的第3个转向平衡点

表7 u=30 km/h和δ=0.1 rad时的第2个转向平衡点

表8 u=30 km/h和δ=0.1 rad时的第3个转向平衡点

求取的转向平衡点，如表9～11所示。由这些表可以看出，应用粒子群算法求解的转向平衡点都能满足设置的精度要求；在某一固定车速下，一共有3个转向平衡点；随着车速增大，第1个转向平衡点值增大，总体变化不大，值减小；第2个转向平衡点的值减小，值先增后减；第3个转向平衡点值减小，值增大。

表9 μ=0.8和δ=0.1 rad时的第1个转向平衡点

表10 μ=0.8和δ=0.1 rad时的第2个转向平衡点

表11 μ=0.8和δ=0.1rad时的第3个转向平衡点

4结论

（1）建立了汽车转向非线性2自由度模型，其中由微分方程和状态方程表示的汽车模型适于任何轮胎模型；给出了转向非线性平衡点的定义，提出了求解转向非线性平衡点的粒子群算法，其为智能算法，易于实现和精度较高，可以达到设置的精度要求。

（2）对3种行驶条件下转向非线性平衡点进行了求解，结果表明，粒子群算法可以求出对应给定精度10-4的3个转向平衡点；随着转角、车速的增加和路面附着系数的减小，转向平衡点的变化范围减小，第1个平衡点会和第2个平衡点相互靠近，为后续的汽车转向非线性稳定性分析与控制提供了前提。