基于改进Zernike矩的铆接孔径亚像素检测方法研究*

张函力，李海伟，于国栋，申 霖，张新喜，纪 俐，3，4

（1. 沈阳航空航天大学，沈阳 110136；2. 航空工业沈阳飞机工业（集团）有限公司，沈阳 110850；3. 沈阳工业大学，沈阳 110870；4. 华晨汽车集团控股有限公司，沈阳 110141）

随着现代航空技术的发展，飞机装配技术正逐步进入智能化、数字化的新阶段[1]。铆钉连接作为飞机蒙皮上的主要连接形式，铆钉孔的加工质量与效率直接影响蒙皮甚至飞机整机结构的性能[2]。许多企业采用自动出钉的铆钉机进行人工铆接，在铆接时对铆钉进行不断敲击，铆钉便会产生一定程度的变形，以此来保证将两个连接面紧密贴合在一起，但人工铆接效率不高。为保证制孔效率，弥补铆钉在加工与装配过程中产生的形变，很多创新型企业纷纷引进基于机器人的在线加工方式完成制孔加工，这样的制造工艺使生产效率得到了保证，铆接工艺迎来了机器视觉时代的曙光。但随之而来的便是制孔后铆钉的质量检测问题。近年来，航空铆钉尺寸检测技术受到重视，然而在国内的生产中，普遍仍以人工通过肉眼进行检测[3]，导致了铆钉尺寸的检测效率很难满足航空工业的需求，使得航空具有潜在的事故风险[4]。

图像边缘是重要的视觉感知信息，也是图像最基本的特征之一。边缘检测作为圆孔视觉测量过程的核心技术[5]，随着实际应用中对检测精度要求的不断提高，传统的像素级边缘检测算法包括Sobel、Prewitt、Laplace算子等，已经无法满足实际需求。因此，人们提出了“亚像素”的概念，针对亚像素级算法的研究也受到越来越多的关注[6]。Zernike矩作为一种特殊的基于Zernike多项式的正交函数的复矩，虽然计算较为复杂，但其具有旋转不变性，在表达能力和噪声敏感性方面具有强大的优势，在目标识别领域得到了广泛的应用[7]。Julier等[8]首次提出了利用Zernike正交矩来检测图像的亚像素边缘，建立了理想的阶跃灰度模型，推导了亚像素坐标的公式。但在实际中由于非理想的离散采样和光学系统衍射效应的限制[9]，往往可能会导致检测边缘附近出现过渡区。

综上，本研究以3D激光轮廓传感器作为图像采集模块，设计出铆接孔径检测系统的整体机械结构，提出了一种改进的基于Zernike矩算法的铆接孔径亚像素检测方法，实现了对锪窝孔外圆孔径的高精度、高效率的检测。

1 检测系统结构设计

本检测系统主要由软件和硬件两部分组成。软件部分在相机已有的Demo文件以及客户端软件3DMVS的图像检测SDK文件开发包的基础上，进行二次开发，并集成Halcon图像深度学习识别算法，利用算法库对采集到的图像进行坐标系统一与数据拼合重构，最终得到铆钉孔径的形貌。硬件部分采用海康威视型号为MV–DP2305–01H的3D激光轮廓传感器，将传感器装配在同步传送装置上，驱动传送装置便可带动光栅尺触发脉冲，使相机在Y方向做直线运动。拟合传感器自身获得的X、Z方向的数据，结合高帧率芯片和激光精准的时序控制，实时输出高精度三维点云数据。采集数据通过千兆网卡传输到计算机上，在客户端软件上设置参数后便可进行测量。测量系统结构框如图1所示。

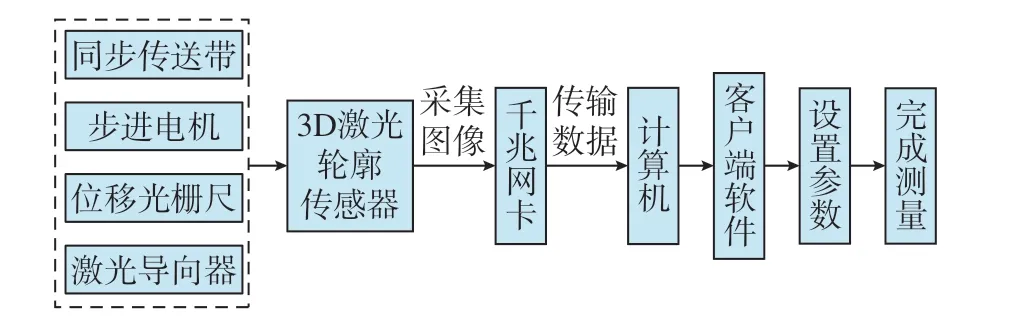
图1 测量系统结构框图Fig.1 Structure block diagram of measurement system

2 锪窝孔径图像处理

2.1 铆接孔图像处理流程

根据采集铆接孔径图像的特点，制定相应的图像处理流程，如图2所示。首先，通过3D激光轮廓传感器获取铆钉孔图像，并对所采集的铆接孔径图进行图像增强处理，然后采用Canny算子边缘检测对锪窝孔内外圆进行边缘识别，利用改进的Zernike矩进行亚像素级的边缘精确检测，提取出锪窝孔外圆的圆环区域，最后结合RANSAC算法进行圆拟合，产生圆轮廓并获取半径，完成测量。

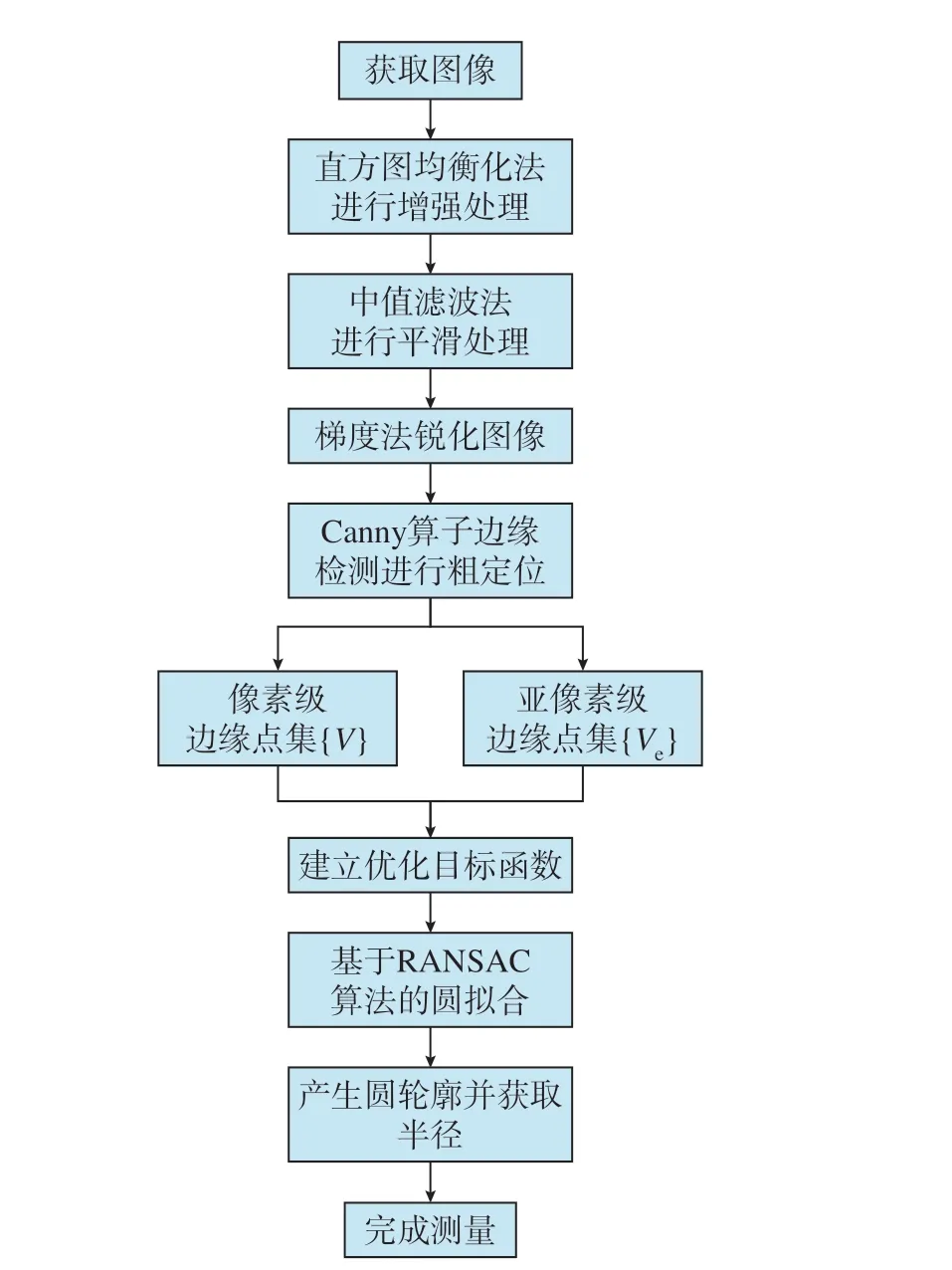
图2 图像处理流程Fig.2 Flow chart of image processing

2.2 图像增强

图像增强是有目的性地强调图像的整体或局部特性，扩大图像中不同特征之间的差别，抑制不感兴趣的特征，使处理结果更适用于机器识别系统。但增强处理并不能增加原始图像信息，只能对某些信息的辨识能力进行提升，满足某些特殊分析的需要。

2.2.1 直方图均衡化法

在数字图像处理中，直方图是一种简单而又实用的工具，它能够描述出图像的概貌，并反映出图像中每一灰度级与其出现像素频率间的统计关系。综合对比增强效果后，选用空间域处理法中的直方图均衡化法。

直方图均衡化法通过对原图像的灰度直方图进行某种变换，可以修正原图像中具有相近灰度值且占有大量像素点的区域，使其灰度范围变宽并均匀分布，以达到增强图像整体对比的效果。

假定r和s分别表示已完成归一化的变换前后的图像灰度，T（r）为变换函数，则二者变换关系为

若想保证灰度变换前后灰度级由黑到白的次序不变，像素灰度值仍在变换前所允许动态范围，则需满足当0≤r≤1时，T（r）为单调递增函数，且0≤T（r）≤1（0代表黑色，1代表白色）。

对于灰度级为离散的数字图像，用频率来代替概率，则灰度级rk出现的频率为

式中，nk表示第k个像素级像素个数，n表示总像素个数。

若设L为灰度级的个数，那么原图像的灰度级为[0，L–1]，为了保证变换前后的灰度值和灰度范围一致，则均衡变换函数T（rk）采用求和方式可表示为

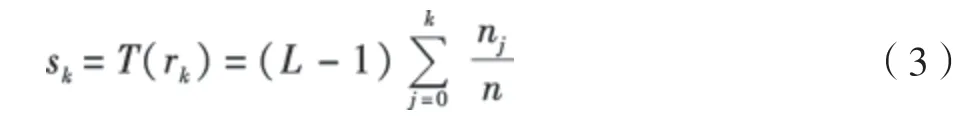
式中，nj表示第j个像素级像素个数。

利用直方图均衡化法对所采集的铆接孔径图进行增强处理后的效果如图3所示。

图3（a）为相机采集的原始成像图，整体颜色偏暗，且各部分颜色不均衡且不分明；图3（b）为灰度化后的图像，相对于图3（a），锪窝孔外圆轮廓更加明显，但内孔轮廓不清晰；图3（c）为使用直方图均衡化后的图像，与图3（a）和（b）两图对比不难看出，图3（c）边缘轮廓处的像素值变化更加明显，且锪窝孔外圆轮廓和内孔轮廓清晰。

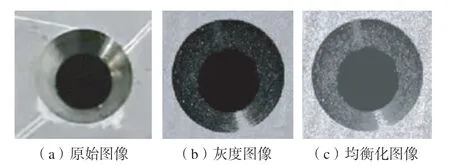
图3 图像增强效果图Fig.3 Sketch of image enhancement

2.2.2 图像平滑

为了抑制噪声，使图像亮度趋于平缓，减小突变梯度，改善图像质量，对图像进行图像平滑处理。均值滤波法虽然算法简单，计算速度快，但经过其处理过的图像在平滑过程中会导致图像边缘模糊化。因此，选用中值滤波法进行平滑处理。

中值滤波是对邻域内的像素灰度值进行排序，用其中值代替中心点像素的灰度值的滤波方法，是一种非线性信号平滑处理技术，能有效消除孤立点和线段的干扰，可以减弱或消除傅立叶空间的高频分量。假设f（x，y）为原始图像，g（x，y）为中值滤波处理后的图像，则中值滤波可以表达为

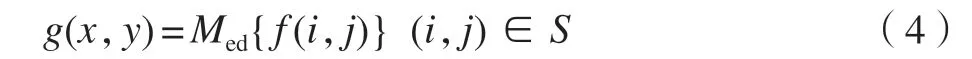
式中，f（x，y）为二维图像数据序列；g（x，y）为中值滤波后的数据；S是以点（x，y）邻域为中心的邻域集合。利用中值滤波法进行平滑处理后的效果如图4所示。

图4 图像平滑效果图Fig.4 Sketch of image smoothing

2.2.3 图像锐化

经过降噪后的图像在图像形成和传输过程中，由于成像系统聚焦不好或者信道的带宽过窄，图像边缘和图像轮廓模糊、细节不清晰。因此，采用图像锐化技术来减少这类不利效果的影响，使图像的边缘轮廓清晰。

Sobel算子结合了高斯平滑和微分求导，采用卷积核对图像中的像素点做卷积运算，拥有x、y两个方向的卷积核，是常用的微分算子。

若将图像经过两个算子的滤波，便可获得增强后的图像灰度值，即

式中，Gx和Gy分别表示图像对应像素中心点的像素在x、y两个方向上的梯度。锐化后的图像如图5所示。

图5 图像锐化效果图Fig.5 Sketch of image sharpening

2.3 图像分割

图像分割本质上是对图像中具有相同特征的区域进行标记的过程，可以进一步对经预处理后的图像进行简化图像分析，根据灰度、形状、颜色等参数的差异，将图像划分为多个不同的子区域，并使这些参数在同一区域内呈现相似性，而在不同区域之间呈现明显的差异性。

2.3.1 基于直方图谷底法的自动阈值分割

为了适应在采集过程中的环境变化，并消除人工设定阈值的主观性，可以运用自动阈值分割方法。自动阈值分割方法是基于图像的灰度直方图来确定灰度阈值，其原理是以灰度直方图中出现的谷底为分割点，对灰度直方图的波峰进行分割。

在HALCON中常用Auto threshold算子进行自动值分割处理，该算子可以对单通道图像进行多重阈值处理，其原理是以直方图出现的谷底为分割点，对灰度直方图的波峰进行处理，效果如图6所示。

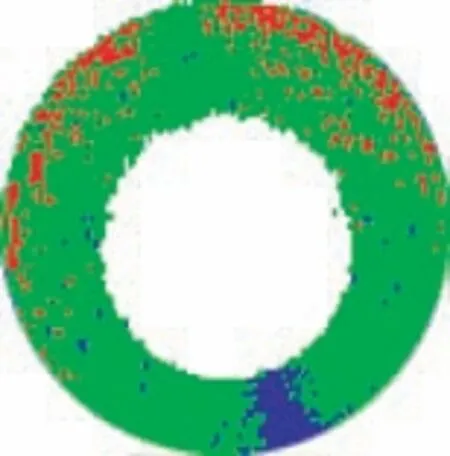
图6 直方图法自动阈值分割Fig.6 Automatic threshold segmentation in histogram

但该方法存在两个难点： （1）在图像分割前，无法确定图像分割生成区域的数目； （2）因为阈值的选择直接影响分割的精度及分割后的图像进行描述分析的正确性，可能会导致阈值分割不准确。可以看出，该方法对铆接孔内外圆环分割不完整。

2.3.2 Prewitt算子边缘提取

Prewitt算子是利用像素邻点之间的灰度差，在边缘处达到极值的方法，从而检测出图形边缘。因此，其对噪声具有一定的抑制能力，但不能完全排除检测结果中出现的虚假边缘，处理后的效果如图7所示。

图7 Prewitt算子边缘提取Fig.7 Edge extraction in Prewitt

Prewitt算子对噪声具有抑制作用，因此对于噪声较多、灰度渐变的图像处理得较好。当某些噪声点的灰度值很大，而对于那些幅值较小的边缘点，其可能会造成边缘点的误判。

2.3.3 Kirsch算子边缘提取

Kirsch算法是一种非线性的边缘检测器，由8个方向的模板决定，将这8个模板的元素与图像上的每一个元素进行卷积求导数，然后筛选出其中的最大值作为中央像素的边缘强度，处理后的效果如图8所示。

图8 Kirsch算子边缘提取Fig.8 Edge extraction in Kirsch

这种方法比较容易得到平滑的边缘，但是由于其方向模板比较有限，对称性可能会减半。因此，很难检测出图像所有的边缘方向。

2.4 基于改进Zernike矩算法的亚像素边缘提取

在综合分析多种边缘检测方法的基础上，本文提出了一种基于改进Zernike矩的亚像素铆接孔径检测方法，采用Canny边缘提取进行像素级的粗定位，并利用改进的Zernike矩算法进行亚像素级的精定位。

2.4.1 Canny边缘提取粗定位

Canny算子是一种多阶段的优化算子，利用高斯函数的一阶微分性质，把边缘检测问题转换为检测准则函数极大值的问题，能在噪声抑制和边缘检测之间取得较好的折中，提取的边缘也相对完整，能够检测出图像较细的边缘部分[10]。

Canny边缘检测的基本思想是首先对图像选择一定的高斯滤波器进行平滑滤波，并计算出平滑后图像G各点处的梯度幅值和梯度方向，获得相应的梯度幅值图像H和梯度方向图像R[11]。则此时点（i，j）处的梯度幅值为

梯度方向为

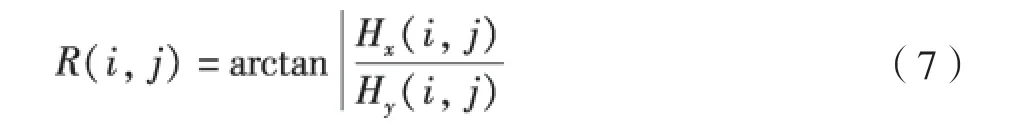
边缘提取后的效果如图9所示。

图9 Canny边缘提取分割Fig.9 Edge extraction and segmentation in Canny

2.4.2 改进的Zernike矩算法的亚像素级精定位

在传统方法中，图像整体采用一个不变的阈值qt，这就导致边缘的检测效果不理想。较为理想的qt值所应该达到的效果是能够根据qt值将像素区分为目标和背景，即让目标和背景的类间方差最大[12]。

假设f（x，y）为一幅图像，Apq为p阶q次的Zernike矩，则当图像为离散形式时，Zernike矩可表示为

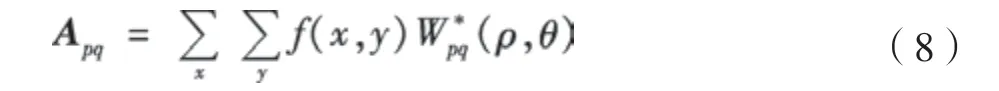
式中，Wp*q（ρ，θ）表示在极坐标系下，共轭的单位圆内的正交p阶q次Zernike多项式[13]。

由于Zernike矩本身是积分形算子，这就使其拥有对噪声不敏感的特性。因此，采用Zernike矩进行亚像素级别的边缘检测。理想的阶跃边缘模型如图10所示[14]。其中，m为背景灰度；l为圆心到边缘的垂直距离；φ为边缘关于x轴所成的角度；n为阶跃高度。

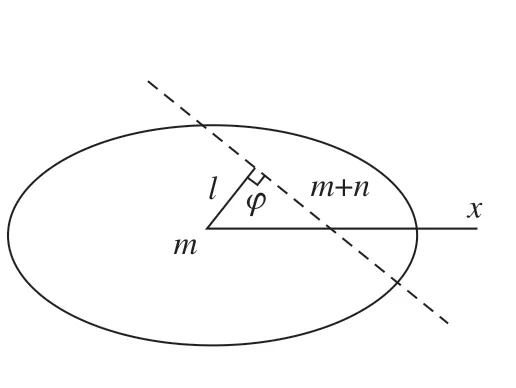
图10 理想阶跃模型[14]Fig.10 Ideal step edge model[14]

如果把边缘旋转角度–φ，则边缘将与y轴平行。此时，有

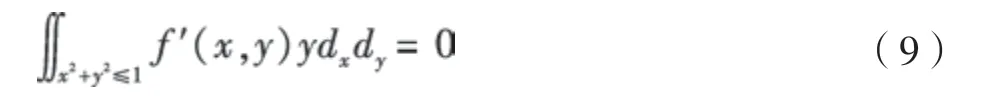
式中，f′（x，y）是旋转后得到的图像边缘函数。

但若仅考虑理想情况下的阶跃模型，便会导致检测出的孔径边缘比较模糊。因此，这里提出对铆钉孔径边缘附近的每一个像素都采用Zernike矩计算其边缘参数的方法。当Zernike模板为N×N时，其亚像素边缘检测公式为

结合铆钉的实际情况，这里设定相对灰度阈值α和强度阈值β，在铆钉孔径边缘附近搜索灰度值低于相对灰度阈值α的区域，并沿着这个梯度方向，找出强度值大于强度阈值β的点，记下其坐标。设像素级边缘点集为{V}，按照式（10）进行计算，生成亚像素点集。

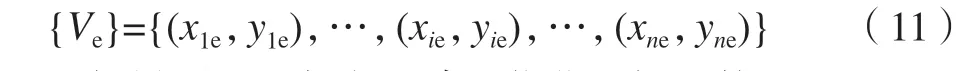
根据椭圆的一般方程建立优化目标函数。

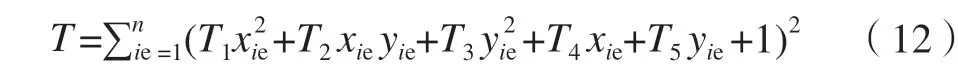
在实际计算过程中，首先利用Canny边缘检测确定铆钉孔径图像的像素级边缘，再利用上述改进的Zernike矩进行亚像素级定位。不仅避免了繁杂的计算，而且能够提取到精确的边缘信息。最终完成了对铆接孔外圆亚像素级的边缘提取，如图11所示。与之前的边缘检测方法相比，该算法检测出的圆孔边缘轮廓信息相对完整，实现了亚像素级的边缘检测。

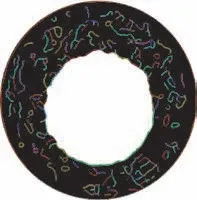
图11 亚像素级的边缘提取Fig.11 Edge extraction in sub-pixel

2.5 基于RANSAC算法的圆拟合

随机抽样一致（RANSAC）算法是一种鲁棒性强，且适用于大比例外点的参数估计算法[15]，最早在1981年由Raguram等[16]提出。该算法的基本假设是样本中包含正确数据，即内点（可以被模型描述的数据）；也包含异常数据，即外点（偏离正常范围很远、无法适应数学模型的数据）。

RANSAC算法的关键是计算出模板图像的特征点与待匹配图像的相应特征点之间的坐标转换关系，即变换矩阵M，变换矩阵和特征点之间关系如式（13）所示[17]。

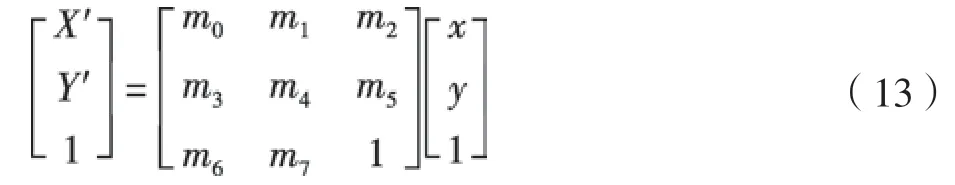
RANSAC算法采用迭代的方式从一组包含局外点的数据中估算出数学模型的参数。经过一定次数的迭代后，选取接近合理解概率最大的样本集，得到最合理解[18]。置信度L与迭代次数K关系式为

RANSAC算法拟合过程排除了局外点的干扰，并估计出高精度的模型参数，拟合结果如图12所示。

图12 RANSAC拟合圆Fig.12 Circle fitting in RANSAC

3 检测试验与数据分析

3.1 检测设置

开始检测前，分别设置锪窝外圆孔径的基准值为7190 μm和极限偏差值为50 μm，即孔径在（7190±50） μm范围内，均为合格孔，否则为不合格孔，如图13所示。

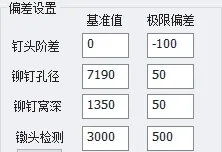
图13 极限偏差设置Fig.13 Limit deviation setting

3.2 检测结果

人工利用内卡规进行测量时，把卡规插入铆接孔中，使测头接触内孔表面，尽量保持测头连线与孔轴线垂直，测头沿孔壁圆周方向摆动，卡规指示最大值即为测量值（直径）。人工检测进行3次测量取其均值，并将其作为参考，检验机器视觉检测结果正确性。为了使检测结果真实准确，选取铆接板上的5行6列共30个铆接位置进行3次重复检测，记录每个位置的铆接孔径尺寸信息，并对测量出的数据进行统计分析，检测结果如图14所示。

图14 检测结果Fig.14 Test results

3.3 数据分析

将3组机器视觉检测的铆接孔径的均值与人工检测的均值数据进行对比，如图15所示。可以看出，两组检测数据的变化趋于一致，而且两条折线在各个节点处相差不超过10 μm。

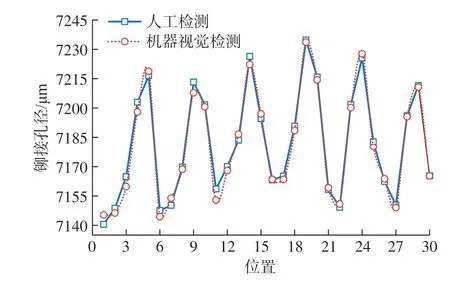
图15 机器和人工检测孔径均值对比图Fig.15 Comparison diagram of mean value of aperture detected by machine and manual

将3次机器视觉检测的铆接孔径数据进行对比，如图16所示。可以看出，3者整体变化趋势基本相同，说明这些位置的3次检测结果大致相同。折线波动部分的检测结果相差不超过10 μm，即铆接孔径的重复测量精度可达到10 μm。

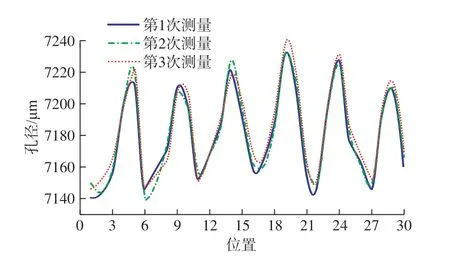
图16 机器视觉3次孔径检测对比图Fig.16 Comparison diagram of cubic aperture detection in machine vision

将机器视觉检测的3次铆接孔径分别与人工测量的均值数据作差，求出各个铆接孔径的差值，并将3组差值进行对比，如图17所示。可以看出，每点相差值均在10 μm以内，说明检测系统具有较高的稳定性。

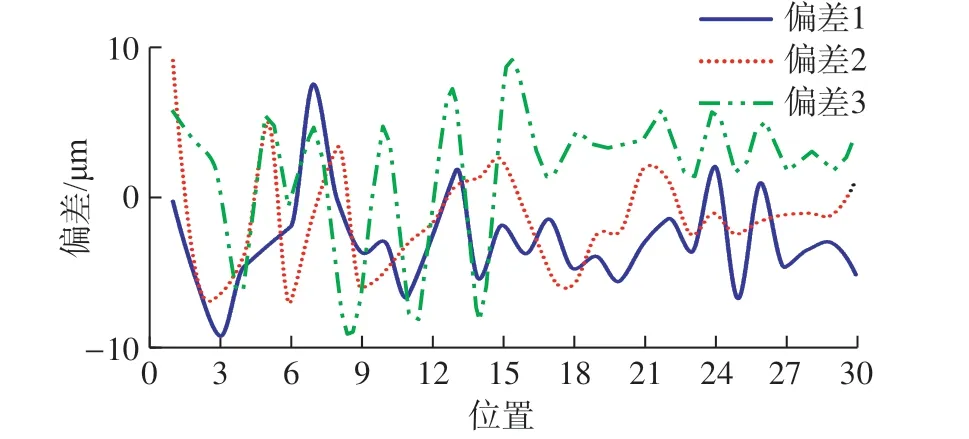
图17 人工和机器视觉测量偏差图Fig.17 Deviation diagram of manual and machine vision measurement

为了更加直观地对比机器视觉检测与人工检测的铆接孔径数据，将二者检测数据的均值做成箱线图，如图18所示。可以看出： （1）箱体在竖直方向的高度反映了数值范围，蓝色箱体整体在红色箱体上方，说明机器视觉检测孔径数值整体偏大； （2）黄色线的位置基本相同，即人工检测和机器视觉检测铆接孔径的中心趋势基本相同； （3）小方块表示异常值，人工与机器视觉检测孔径时，各出现1个异常点，说明二者都具有良好的检测稳定性； （4）紫色线为非异常范围内的最大值和最小值，即机器视觉检测铆接孔径极差更小； （5）箱体的宽度反映了数据的散布情况，说明二者检测孔径分布情况基本相同。

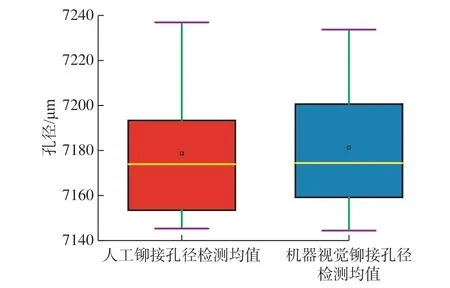
图18 人工和机器视觉测量箱线图Fig.18 Box diagram of manual and machine vision measurement

4 结论

（1）针对飞机铆接孔径的检测问题，本研究提出了一种改进的基于Zernike矩算法的亚像素级边缘检测方法。该方法检测出的圆孔边缘轮廓信息相对完整，实现了亚像素级的边缘检测。

（2）设计了锪窝孔外圆直径检测系统，在对30个位置的铆接孔径进行重复检测，并与人工检测结果对比后，证明该系统检测结果的偏差值在±10 μm范围内，重复测量精度可达到10 μm。

（3）该检测系统可以同时测量多个位置的孔径，实现了对铆接孔径的高精度、高效率测量。