中美通信铁塔独立基础计算差异分析

程骞，高海江

(中兴通讯股份有限公司，南京 210012)

1 引言

随着我国通信技术实力的不断发展，中国企业在海外的通信基础设施建设规模也在不断增长，例如，中兴通讯在菲律宾的DITO 项目，新建铁塔站点数量多，土建设计方案对整个项目的工程成本具有重要影响。菲律宾结构设计规范大多借鉴美国标准，为了适应海外项目建设需求，有必要对以美国标准为代表的国外设计规范进行深入解读并分析其与中国规范的差异。

地基承载力、基底脱开面积、抗倾覆稳定、抗拔稳定对独立基础的尺寸、埋深起到决定性作用，从而对工程成本产生关键影响。本文就以上验算内容逐项讨论，结合算例，分析中美规范差异及其对设计结果的影响，为海外铁塔工程成本及方案优化提供一定参考价值。

2 地基承载力验算

2.1 两国规范设计方法对比

由于土壤相比钢筋混凝土结构具有高变异性，基于极限状态设计法(LSD）的荷载与抗力分项系数法(LRFD）研究尚不成熟，我国GB 50007—2011《建筑地基基础设计规范》[1]地基承载力验算采用容许应力法(ASD），基底压应力采用相应于荷载标准组合的值，地基承载力采用特征值。

美国TIA-222-F 版规范[2](以下简称“F 版”）中地基承载力验算也是采用ASD 法，地基承载力采用容许承载力。

美国TIA-222-G 版[3]和TIA-222-H 版[4]规范(以 下简称“G版”“H 版”）地基承载力验算均采用LRFD 法，基底压应力的采用在概念上相当于我国的基本组合值。两版规范风荷载分项系数不同，G 版采用1.6，H 版采用1.0，原因在于两版风速重现期规定有区别，对于普通铁塔，如果采用重现期50年的风速计算风荷载WL，则风荷载分项系数都应取1.6。

美国标准G 版和H 版地基承载力设计值采用标称承载力(nominal soil resistance）乘以一个小于1 的抗力分项系数φs。标称承载力对应土壤发生剪切破坏的极限承载力。对于自立式铁塔独立基础，G 版和H 版的抗力分项系数φs都取0.75。

2.2 地基承载力确定方法对比

美国规范里没有明确指定地基承载力的确定方法，国际上应用较为普遍的是太沙基公式及其衍生公式[5]。我国GB 50007—2011《建筑地基基础设计规范》根据土壤剪切参数计算地基承载力的公式和太沙基理论公式类似。

以方形基础为例，太沙基理论计算如式(1）：

我国标准计算公式可表达如式(2）：

式中，qu为地基发生一般剪切破坏相应的极限承载力，采用ASD 法验算时，需除以安全系数得到容许承载力qa，而地基承载力特征值fa是考虑了安全系数的；c′为黏聚力，q 为基底埋深处的土压应力；γ 为基底处土的有效重度；B 为基底宽度；Nc、Nq、Nγ和Mc、Md、Mb都是与内摩擦角有关的系数，具体如表1所示。

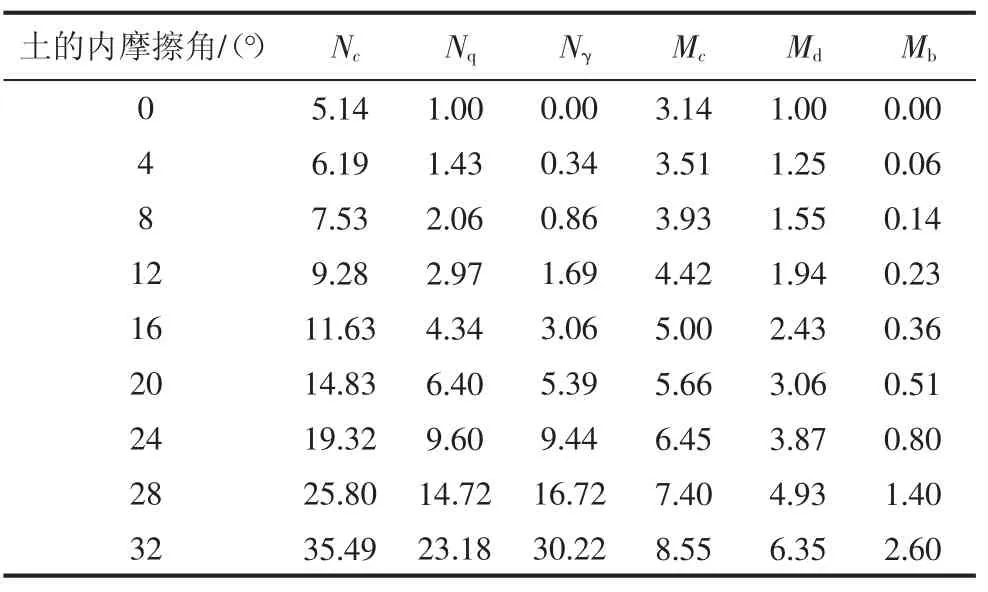
表1 两种地基承载力计算公式中和内摩擦角有关的系数

从表1数值可以看出，我国规范公式参数随内摩擦角增大的幅度较缓，也就是说内摩擦角越大的土层，我国规范计算结果相对越保守，但是由于不同地基承载力确定方法的适用条件不一，且考虑的修正、安全系数不尽相同，实际工程中建议结合当地工程经验选用。

2.3 各版规范设计差异对比

美国标准F 版地基承载力验算式可表达为：

式中，pk为标准组合荷载作用下的基底压应力，qa为地基容许承载力。

美国标准G 版、H 版规定，若土测资料没有明确安全系数，则按安全系数2 反推极限承载力，即地基极限承载力qu=2qa的关系，于是G 版和H 版的验算式可表达为：

仅考虑恒荷载DL和风荷载WL时，pk为荷载1.0DL+1.0WL组合相应的基底压应力，p 为荷载1.2DL+1.6WL组合相应的基底压应力，根据大量铁塔设计经验，p 一般为1.35～1.4 倍pk。通常的地勘资料安全系数都不小于2，因此，美国标准F 版地基承载力验算往往比G 版、H 版更保守些。

我国规范地基承载力验算式和美国标准F 版一致，但是对相应于偏心荷载作用下的基底压应力，其地基承载力验算考虑了1.2 的地基承载力加强系数。可见，单从地基承载力验算式上来看，美国标准F 版相比我国标准也更保守些。

3 基底脱开面积控制、抗倾覆稳定性验算

铁塔为主要承受水平风荷载的结构，铁塔基础需要抵抗水平风荷载产生的倾覆弯矩，对于单管塔独立基础，需重点验算基底脱开面积和抗倾覆稳定性。

3.1 基底脱开面积百分率、荷载偏心率、抗倾覆稳定安全系数之间的关系

根据三角形分布基底反力模型，荷载偏心率e/B，基底脱开面积百分率X 和抗倾覆稳定安全系数k 的关系可做如下推导。

如图1所示，基底宽度为B，上部结构传至基础底板的荷载为N，偏心距e，三角形分布基底反力作用合力点位于三角形形心，和N 的作用点相同，其距基础边缘的距离为a=B/2-e，则三角形分布基底反力作用宽度为3a，基底脱开宽度即零应力区宽度为B-3a=3e-B/2，于是基底脱开面积百分率X 为：

在上述偏心荷载作用下，相当于一个大小为N 的竖向作用力和一个大小为Ne 的弯矩作用于基础底板形心，Ne 即倾覆弯矩，抗倾覆弯矩为N·B/2，于是抗倾覆安全系数k=B/(2e）。综上，三者之间关系如式(6）：

3.2 我国及美国各版规范有关规定及对比

我国YD/T 5131—2019《移动通信工程钢塔桅结构设计规范》[6]规定，荷载标准组合下，基底脱开面积不超过1/4，同时规定了抗倾覆稳定安全系数为2.0。美国标准F 版规定的抗倾覆安全系数是1.5。美国标准H 版则规定考虑分项系数的荷载组合下，荷载偏心距不超过基底宽度的45%。美国标准G 版未做相关规定。

于是，美国标准F 版相当于规定了基底脱开面积百分率不超过50%(荷载标准组合），H 版相当于规定了基底脱开面积百分率不超过85%(考虑分项系数的荷载组合）。可见，对于单管塔独立基础，地基承载力足够时，按美国标准TIA 系列设计的基础尺寸比我国标准要小。

4 基础抗拔稳定性验算

在风荷载产生的倾覆弯矩作用下，格构式铁塔独立基础会承受较大的上拔力，需进行抗拔稳定性验算。

4.1 两国规范设计方法及相关参数对比

4.1.1 我国规范设计方法

我国标准抗拔稳定验算也是采用的ASD 法。我国YD/T 5131—2019《移动通信工程钢塔桅结构设计规范》规定抗拔验算宜采用土重法，即基础所受拔力完全由基础自重Gc和其上抗拔角范围内的土体自重Gs抵抗。拔力Fuk采用标准组合值，土重安全系数取2.0，基础重安全系数取1.4。公式可表达如式(7）：

4.1.2 美国规范设计方法

美国标准里也给出了土重法抗拔验算的公式或参数。美国标准F 版和我国标准类似，其公式可表达如式(8）：

拔力同样采用标准组合值，土重安全系数2.0，基础重安全系数1.25，且还应满足总体安全系数1.5。

美国标准G 版和H 版都是采用LRFD 法，拔力采用乘分项系数的组合值Fu，抗拔力乘抗力折减系数，基础自重Gc和其正上方柱体内土重Gs1的抗力折减系数取0.9，柱体以外土体Gs2的抗力折减系数取0.75，其验算式如式(9）：

以下采用典型算例对各版规范抗拔验算进行对比。

4.2 算例

某独立基础底板尺寸4 m×4 m，底板厚度0.45 m，基础短柱尺寸0.7 m×0.7 m，短柱出地面高度0.1 m，基础埋置于某黏性土层中，抗拔角取25°，埋深3 m，土重度16 kN/m3，混凝土重度24 kN/m3，地下水位于基础底面以下，用土重法计算该基础可承受的最大上拔力。

按各版规范计算出的该基础可承受最大上拔力计算值如下：

我国标准：Fuk＝694.6 kN； 美国标准F 版：Fuk＝718.9 kN；美国标准G 版、H 版：Fu＝1 101.9 kN。

其中，我国标准和美国标准F 版的Fuk相应的拔力为1.0DL+1.0WL荷载组合下的拔力，美国标准G 版、H 版Fu相应的拔力为0.9DL+1.6WL(WL为50年重现期风速作用下的风荷载）荷载组合下的拔力，同样的荷载作用下，两种组合相应的拔力计算值是大于1.6 倍的关系，而抗拔力计算值的比值1 101.87/718.89=1.53＜1.6。由该算例可见，我国标准和美国标准G 版、H 版的抗拔稳定性验算要比F 版保守。

5 结论

1）关于地基承载力的确定方法，中国和美国差异较大，且修正系数、安全系数不尽相同，建议结合当地工程经验选用。美国标准G 版和H 版相比F 版，其地基承载力验算结果更经济。

2）美国标准F 版和H 版对基底脱开、抗倾覆稳定验算的规定比我国标准要宽松。因此，对于单管塔独立基础，地基承载力足够时，按美国标准TIA 系列设计的基础尺寸比我国标准要小。建议我国规范进一步研究铁塔基础抗倾覆安全系数是否具有优化空间。

3）对于格构式自立铁塔，当上拔工况对基础尺寸起控制作用时，按美国标准F 版设计的基础通常要比G 版、H 版及我国标准要更经济。