战争策略算法与变色龙算法优化极限学习机的输沙量时间序列预测
许建伟,崔东文
(1.云南省水利水电勘测设计院,云南 昆明 650021;2.云南省文山州水务局,云南 文山 663000)
作者简介:许建伟(1984—),男,云南楚雄人,高级工程师,主要从事水利水电工程规划、建设征地移民安置等工作;崔东文(通讯作者).
1 研究背景
泥沙问题一直都是水土流失治理的重点,提高输沙量预测精度对于区域水土流失治理、防洪减灾、水资源科学调度以及河势演变、取水工程防淤治理均具有重要意义。输沙量时间序列预测是依据已有的历史监测数据,通过科学的方法推测将输沙量的变化趋势,以期达到撑握输沙量现状及发展趋势的目的。与径流预测相比,输沙量受径流、气候、人类活动等众多因素影响,不仅预测难度大,缺少成熟、适用的模型与方法;而且时序数据表现出高噪声、非线性、非平稳性和多尺度等多重特征,神经网络[1-3]、支持向量机[4]、灰色预测[5]等单一模型难以获得满意的预测效果。当前,基于“分解算法+预测模型+叠加重构”的预测方法已在径流或降水时间序列预测中得到广泛应用,但在输沙量预测研究中应用较少,如陶望雄等[6]基于经验模态分解(EMD)和自回归方法构建预测模型对泾河年输沙量进行预测,结果表明该模型适用性较好,模拟精度高,可应用于年输沙量预测;王俊杰等[7]提出自适应噪声完备经验模态分解(CEEMDAN)耦合小波神经网络(WNN)的输沙量预测模型,通过黄河利津站输沙量预测实例对CEEMDAN-WNN进行验证,结果表明该模型比BP神经网络和小波神经网络精度更高,能够实现对水沙序列的准确预测。然而,在实际应用中,EMD模态混叠问题使其分解存在局限性,难以获取有效信息;CEEMDAN在一定程度上解决模型混叠问题,但仍然存在计算量大、复杂度高等问题;自回归模型显然难于应对复杂的时间序列预测问题;小波神经网络反向传播算法存在着易陷入局部极值和对初值要求较高等不足。
小波包变换(Wavelet Packet Transform,WPT)源于小波分解,它在分解信号低频子集同时,对高频子集继续分解,具有数学释意明确、使用简洁、能够自行设定分解层数和分解效果好等特点,已在含沙量预测研究中得到应用[8]。极限学习机(Extreme Learning Machine,ELM)是一种快速学习算法,用于训练单隐层前馈神经网络,具有自主学习、学习速度快、泛化能力强等特点,已在各行业领域得到应用。在实际应用中,由于ELM初始权值和隐含层偏置(超参数)是随机选取的,致使ELM网络性能难以达到最优。目前,粒子群优化(PSO)算法[9]、果蝇优化算法[10]、灰狼优化(GWO)算法[11]、鲸鱼优化算法(WOA)[12]、黑猩猩优化算法(ChOA)[13]、樽海鞘群算法(SSA)[14]、鸟群算法(BSA)[15]等群体智能算法(Swarm Intelligence Algorithms,SIA)已在优化ELM超参数中得到应用。为提高输沙量时间序列预测精度,本文基于WPT、战争策略优化(War Strategy Optimization,WSO)算法、变色龙群算法(Chameleon Swarm Algorithm,CSA)和“分解算法+预测模型+叠加重构”思想,建立WPT-WSO-ELM、WPT-CSA-ELM输沙量时间序列预测模型,并构建WPT-ELM模型以及基于小波变换(Wavelet Transform,WT)的WT-WSO-ELM、WT-CSA-ELM、WT-ELM作对比分析模型,通过云南省龙潭寨1968年~2013年汛期、枯期输沙量时序数据对各模型预测性能进行验证。
2 方法描述
2.1 小波包变换(WPT)
小波包变换(WPT)通过低通滤波器H和高通滤波器G将信号数据分解为低频信号和高频信号序列各一组,然后将各层的频带进一步分解为其下一层的2个子频带,以此类推实现多层分解。利用WPT对原始信号进行分解的公式[16-18]为
(1)
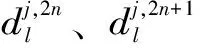
重构算法如下
(2)
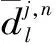
2.2 极限学习机(ELM)
给定M个样本Xk={xk,yk},k=1,2,…,M,其中,xk为输入数据,yk为真实值,f(·)为激活函数,隐层节点为m个,ELM输出可表示为
(3)
式中,oj为输出值;Wi={wi1,wi2,…,wim}′为输入层节点与第i个隐含层节点的连接权值;bi为第i个输入节点和隐含层节点的偏值;λi为第i个隐含层节点与输出节点的连接权值。
2.3 战争策略优化(WSO)算法
WSO是Ayyarao等人于2022年提出一种基于古代战争策略的新型元启发式优化算法[19]。该算法灵感来自于古代战争中的攻击策略和防御策略,并通过士兵在战场上的位置更新来达到求解优化问题的目的。WSO基于以下假设:①军队士兵随机分布于战场并攻击对方军队;攻击力最强的士兵为指挥官;国王是军队的最高领袖。②士兵根据国王和指挥官的位置动态更新位置。③国王根据战场上的局势通过战鼓动态地改变策略。④士兵根据附近士兵位置和国王位置来改变其位置。⑤对于战斗力最低的士兵或受伤的士兵,通过新兵替换或重新安置的策略进行位置更新。⑥所有士兵都有同等的概率成为国王或指挥官。
参考文献[19],WSO数学描述如下。
(1)攻击策略。士兵根据国王和指挥官的位置来更新自己的位置。数学描述为
Xi(t+1)=Xi(t)+2×rand×(C-King)+
rand×(Wi×King-Xi(t))
(4)
式中,Xi(t+1)为第t+1次迭代士兵新位置;Xi(t)为第t次迭代士兵位置;C为指挥官位置;King为国王位置;rand为介于0和1之间的随机数;Wi为国王位置的权重。
(2)排序和权重。士兵的等级Ri取决于他在战场上的攻击力(适应度值)。若士兵新位置的攻击力Fn小于前代位置的攻击力Fp,则士兵占据前一个位置。数学描述为
Xi(t+1)=(Xi(t+1))×(Fn≥Fp)+
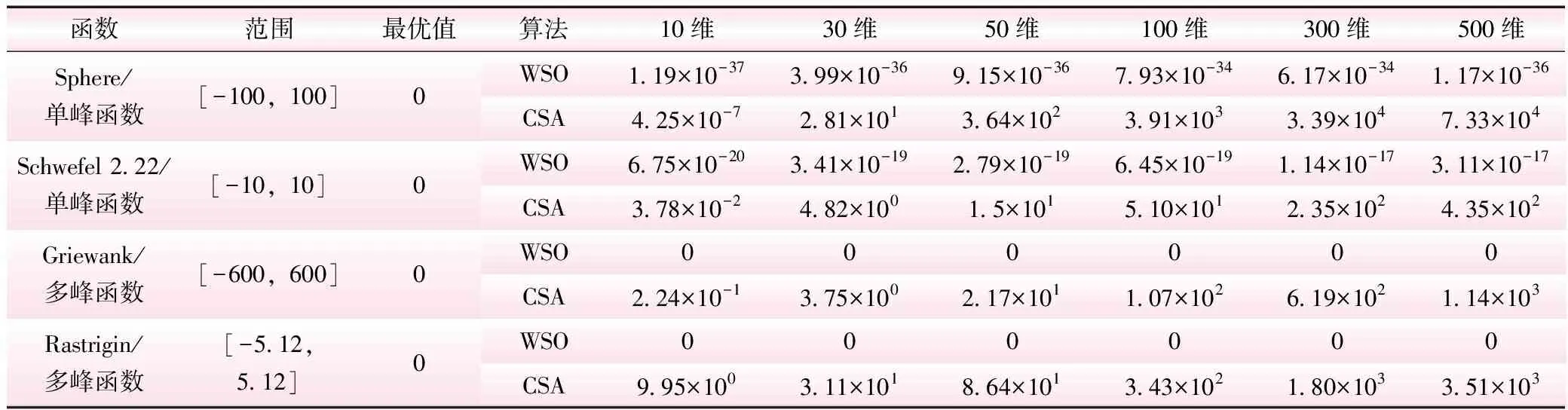
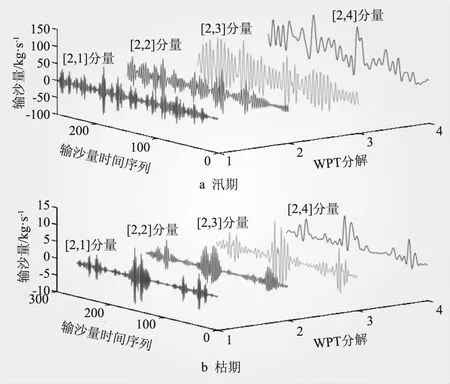
(Xi(t))×(Fn (5) 若士兵成功更新位置,则士兵等级Ri将得到提升。数学描述为 Ri=(Ri+1)×(Fn≥Fp)+(Ri)×(Fn (6) 根据士兵的攻击力(适应度值)进行排序,权重更新数学描述为 Wi=Wi×(1-Ri/T)α (7) 式中,Fn为士兵新位置攻击力(适应度值);Fp为士兵前代位置攻击力(适应度值);Ri为第i个士兵的等级;α为指数变化因子。 (3)防御策略。士兵根据附近士兵位置和国王位置来改变其位置,并在不输掉战斗的情况下最大限度地保护国王。数学描述为 Xi(t+1)=Xi(t)+2×rand×(King-Xrand(t))+ rand×Wi×(C-Xi(t)) (8) 式中,Xrand(t)为第t次迭代士兵的随机位置;其他参数意义同上。 (4)替换或安置弱兵。WSO利用两种方式更新弱兵位置:一是利用式(9)中给出的随机士兵位置替换弱兵位置;二是通过式(10)将弱兵安置到更靠近整个战场中位数的位置,这将有利于提高算法的收敛性。 Xw(t+1)=Lb+rand×(Ub-Lb) (9) Xw(t+1)=-(1-randn)× (Xw(t)-median(X))+King (10) 式中,Xw(t+1)为第t+1次迭代替换或安置的弱兵位置;Ub、Lb为搜索空间的上、下限值;Xw(t)为第t次迭代弱兵位置;randn为0和1之间均匀分布的随机数;median(·)为中位数函数。 CSA是Braik于2021年提出的一种基于变色龙觅食策略的新型元启发式优化算法[20-21]。该算法主要通过搜索猎物、眼睛旋转发现猎物和捕捉猎物三阶段的位置更新来求解优化问题。 参考文献[20-21],CSA数学描述如下: (1)初始化。CSA通过随机初始化变色龙种群个体开始,每个个体均为目标问题的候选解。设在d维搜索空间中,种群规模为n的变色龙个体初始位置 xij=Ub+r×(Ub-Lb) (11) 式中,xij为第i只变色龙第j维空间位置;r为(0,1)范围均匀生成的随机数。 (2)搜索猎物。变色龙群体在觅食过程中主要通过式(12)进行位置更新来搜索和发现食物。位置更新数学描述为 (12) (3)眼睛旋转发现猎物。变色龙的眼睛能360°旋转进行猎物搜索,并根据猎物的位置来更新自已的位置。位置更新数学描述为 (13) (4)捕捉猎物。当猎物离变色龙较近时,变色龙便利用舌头攻击猎物并捕捉猎物。位置更新数学描述为 (14) 选取Sphere等4个基准函数在不同维度下对WSO、CSA进行仿真测试,见表1。基于Matlab 2018a M语言实现对4个基准函数的20次寻优,采用平均值进行性能评估。设置WSO、CSA最大迭代次数为200,士兵及变色龙群体规模为50,其他参数设置采用各算法默认值。 表1 标准测试函数寻优结果 对于单峰函数,WSO在不同维度寻优精度均在3.11×10-17以上,较CSA提高19个数量级以上;对于多峰函数,WSO在不同维度寻优均获得理论最优值0,寻优精度远优于CSA。可见,WSO在不同维度下寻优精度及全局搜索能力均优于CSA,具有较好的寻优效果,且寻优精度基本不受维度变化的影响;CSA寻优效果受维度变化影响显著,寻优精度随维度的增加而降低。 步骤一:基于dmey小波包基,分别采用2层WPT和db3小波对龙潭寨1968年~2013年汛期、枯期逐月输沙量时序数据进行分解,分别得到4个子序列分量[2,1]~[2,4]和1个低频率分量rA3、3个高频率分量rD1、rD2、rD3,见图1(限于篇幅,逐月输沙量时序数据WT分解图从略)。 图1 逐月输沙量时序数据WPT分解 步骤二:在延迟时间为1的条件下,采用Cao方法(Cao方法为虚假邻近点法FNN的改进算法)确定子序列分量[2,1]~[2,4]和rA3、rD1、rD2、rD3的嵌入维度K,并利用前n个月的输沙量分量来预测当月输沙量分量,最后将各输沙量分量的预测结果叠加即得到最终月均输沙量的预测结果。输沙量分量预测动态系统描述为 yn=f(xn-1,xn-2,…,xn-K) (15) 式中,yn为当月输沙量预测值;n为月输沙量序列长度;K为嵌入维或滞后数。通过Cao方法计算,汛期、枯期分量[2,1]~[2,4]的K值分别为11、17、13、12和6、16、19、24;汛期、枯期rA3、rD1、rD2、rD3的K值分别为17、13、11、7和13、19、12、15。利用1968年1月~2003年12月月均输沙量作为训练样本,2004年1月~2013年12月月均输沙量作为预测样本。 步骤三:利用各分量训练样本构建WSO、CSA优化ELM超参数的适应度函数f(·) (16) 步骤四:WSO、CSA参数设置同“2.5算法验证”。初始化士兵或变色龙位置,令当前迭代次数t=1。 步骤五:计算士兵或变色龙个体适应度值minf;保存当前最佳士兵或变色龙位置。 步骤六:对于WSO,若r<0.5,利用式(8)更新士兵位置;否则利用式(4)更新士兵位置;计算每个士兵的攻击力(适应度值),对每个士兵的适应度值进行排序,并利用式(5)更新每个士兵位置;利用式(6)、(7)更新士兵等级和权重;通过每次迭代识别出适应度最差的弱兵,基于式(9)、(10)更新弱兵位置。 步骤七:对于CSA,分别基于式(12)~式(14)搜索猎物策略、眼睛旋转发现猎物策略、捕捉猎物策略更新变色龙位置。 步骤八:利用更新后的士兵或变色龙位置计算适应度值minf,比较并保存当前最佳士兵或变色龙位置。 步骤九:令t=t+1,判断算法是否达到终止条件,若是输出最优适应度值和最佳士兵或变色龙位置,算法结束;否则,返至步骤六。 步骤十:输出最优适应度值minf和最佳士兵或变色龙位置。最佳士兵或变色龙位置即为ELM最佳超参数。利用ELM最佳超参数建立4种模型对各子序列分量进行预测,将预测结果叠加即得到输沙量最终预测结果。 云南省龙潭站始建于1951年,断面以上集水面积3 128 km2,河长114 km,平均坡降0.3%,为盘龙河上游主要控制站。盘龙河发源于红河州蒙自县三道沟,流经砚山、文山等5县(市),于天保口岸注入越南,交泸江汇入红河。盘龙河泥沙主要受大气降水和径流的影响,龙潭站多年平均输沙量66.4万t,含沙量为0.898 kg/m3,最大值集中在5月~9月,尤以6月~9月含沙量较大;最小值集中在1月~3月。由于汛期、枯期输沙量起伏变化十分激烈,为有效提高输沙量预测精度,本文按汛期(5月~10月)、枯期(1月~4月、11月~12月)划分输沙量时间序列。即以龙潭站1968年1月~2013年12月汛期、枯期月均输沙量时间序列为研究对象,选取1968年1月~2003年12月月均输沙量作为训练样本,2004年1月~2013年12月月均输沙量作为预测样本,输沙量变化曲线及训练、预测样本见图2。 图2 逐月输沙量时间序列变化 本文选取平均绝对百分比误差(MAPE)、平均绝对误差(MAE)、均方根误差(RMSE)对各种模型进行评估。即 (17) (1)WPT-WSO-ELM、WPT-CSA-ELM、WT-WSO-ELM、WT-CSA-ELM模型:WSO、CSA参数设置同“2.5算法验证”;ELM网络激活函数选择sigmoid,ELM隐层节点数设置为2K-1,分解分量时序数据采用[-1,1]进行归一化处理。 (2)WPT-ELM、WT-ELM模型:为验证WSO、CSA优化ELM超参数的效果,ELM模型相关参数设置同上。 基于“2.6建模流程”实现各模型对龙潭站汛期、枯期输沙量时序数据的训练及预测,预测结果见图3~4,预测相对误差效果见图5。 图3 汛期月均输沙量预测结果误差对比分析 依据图5~7可以得出以下结论: 图5 月均输沙量预测相对误差效果 (1)对于汛期输沙量,WPT-WSO-ELM模型预测的MAPE、MAE、RMSE分别为5.84%、0.574kg/s和0.731kg/s,MAPE较WT-WSO-ELM、WPT-CSA-ELM提高56.5%以上,较WT-CSA-ELM提高79.6%,较WPT-ELM、WT-ELM提高90.2%以上;MAE较WT-WSO-ELM、WPT-CSA-ELM提高36.4%以上,较WT-CSA-ELM提高70.8%,较WPT-ELM、WT-ELM提高83.8%以上;RMSE较WT-WSO-ELM、WPT-CSA-ELM提高38.0%以上,较WT-CSA-ELM提高70.1%,较WPT-ELM、WT-ELM提高84.9%以上。对于枯期输沙量,WPT-WSO-ELM模型预测的MAPE、MAE、RMSE分别为6.73%、0.017kg/s及0.022kg/s,MAPE较WT-WSO-ELM提高60.1%,较WPT-CSA-ELM、WT-CSA-ELM提高83.2%以上,较WPT-ELM、WT-ELM提高92.4%以上;MAE较WT-WSO-ELM提高57.5%,较WPT-CSA-ELM、WT-CSA-ELM提高85.3%以上,较WPT-ELM、WT-ELM提高93.3%以上;RMSE较WT-WSO-ELM提高58.5%,较WPT-CSA-ELM、WT-CSA-ELM提高86.7%以上,较WPT-ELM、WT-ELM提高94.1%以上。这表明WPT-WSO-ELM模型具有更高的预测精度,将其用于输沙量时间序列预测是可行的。 图4 枯期月均输沙量预测结果误差对比分析 (2)在同一WPT分解或WT分解的情形下,WSO优化ELM网络的预测误差要小于CSA优化ELM网络的预测误差,远小于未经优化的ELM网络误差,表明WSO、CSA能有效优化ELM超参数,提高ELM预测性能;算法寻优能力越强,获得的ELM超参数越优,由此构建的ELM模型预测效果越好。 (3)在同一WSO或CSA优化的情形下,基于WPT分解的模型,其预测误差要远小于基于WT分解的模型,表明WPT能将输沙量时序数据分解为更具规律的子序列分量,分解效果要优于WT。 提高输沙量时间序列预测精度对于水土流失防治具有重要意义。本文综合考虑输沙量时序数据的多尺度、高度非线性等多重特征,提出了耦合的WPT-WSO-ELM、WPT-CSA-ELM输沙量时间序列预测模型,并构建WT-WSO-ELM、WT-CSA-ELM、WPT-ELM、WT-ELM对比预测模型,通过龙潭站汛期、枯汛输沙量实例进行验证,得到如下结论: (1)对于基准函数,WSO寻优值均小于CSA,具有较好的寻优精度及全局搜索能力。WSO寻优精度基本不受维度变化的影响,CSA寻优精度随维度的增加而降低。 (2)WPT-WSO-ELM模型的预测误差小于WPT-CSA-ELM模型及WT-WSO-ELM、WT-CSA-ELM模型,远小于WPT-ELM、WT-ELM,具有较好的预测精度和泛化能力,将其用于输沙量时间序列预测是可行的。模型不但预测效果好,而且智能化水平高,可为相关输沙或含沙量时间序列预测研究提供新途径。 (3)WSO、CSA能有效优化ELM超参数,大大提高了ELM的预测性能;WSO的优化效果要优于CSA;算法寻优能力越强,获得的ELM超参数越优,由此构建的ELM模型预测效果越好。 (4)WPT能同时对高频、低频信号进行分解,可将输沙量时序数据分解为更具规律的子序列分量,其分解效果要优于WT。2.4 变色龙群算法(CSA)
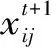
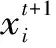

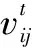
2.5 算法验证
2.6 建模流程

3 实例应用
3.1 数据来源

3.2 评价指标
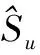
3.3 参数设置
3.4 结果及分析



4 结 论

