融合随机森林和SHAP方法的灌区用水调度经验分析——以淠史杭灌区瓦西干渠灌域为例

苏 楠，章少辉, ，白美健, ，张宝忠,

（1.中国水利水电科学研究院，北京 100038；2.流域水循环模拟与调控国家重点实验室，北京 100038）

▪区域农业水管理▪

融合随机森林和SHAP方法的灌区用水调度经验分析——以淠史杭灌区瓦西干渠灌域为例

苏 楠1，章少辉1,2*，白美健1,2，张宝忠1,2

（1.中国水利水电科学研究院，北京 100038；2.流域水循环模拟与调控国家重点实验室，北京 100038）

【目的】定量表征灌区积累丰富的用水调度经验，使其能够被其他管理人员复制和应用。【方法】本文基于淠史杭灌区瓦西干渠灌域的3个典型年实测数据样本，在充分考虑温度、降雨和土壤墒情等特征变量的空间变异基础上，通过融合随机森林模型和SHAP方法，构建有限数据样本下灌区用水调度目标流量与各特征变量之间的非线性定量表征。【结果】应用该方法可得到长时间序列以及不同典型年情境下各特征变量的重要性得分及变化情况，在找到适用于实际用水调度特征变量组合的同时，可分析得到不同调度情景下主要参考的特征变量指标；结合SHAP值正负情况分析，还可得到用水调度目标流量对各特征变量响应的正负方向。【结论】本文所用方法实现了灌区用水调度历史经验的定量知识化表征，为理性预测未来不同用水调度流量提供科学依据。

淠史杭灌区；用水调度；随机森林模型；SHAP方法；特征变量；非线性表征

0 引 言

【研究意义】灌区是一个典型的自然和社会因素双重驱动演化的复杂水资源系统，也是国家水网建设的重要内容。优化灌区用水调度，对提高全局用水效率、实现水资源可持续发展具有重要意义。【研究进展】当前多数灌区真实的用水调度过程，主要依赖于灌区用水调度人员多年的历史经验。若以用水调度的目标流量作为决策结果，影响目标流量的原因要素众多，需用多个特征变量描述，而这些特征变量既有定性的也有定量的，且某一特征变量可能源于不同空间分布测点，由此形成了依赖于历史经验的复杂逻辑决策网络。该决策网络是灌区用水调度人员经过长期学习试错历练，被固化在其潜意识思维中，外在表现出能科学理性预测灌区用水调度过程的能力。要想模型化该决策网络，进而使其能够迅速被其他用水调度人员应用，需总结其特征，由此寻找适宜的数学建模工具。该决策网络具有3个典型特征，一是其形式是一个复杂网络，二是由于历史原因迄今灌区用水调度实测的数据样本数量有限，三是影响该网络目标流量的特征变量具有显著的自然与社会双重特征。目前灌区用水调度多基于水文学或水文-水力学耦合模型[1-4]，以及能在决策网络中将影响决策结果的主要要素抓取出来的主成分分析法、GIS空间分析与传统确定性系数相结合的方法、多因子综合评价法[5-7]等，都难有效同时应对上述3个特征。灌区用水调度的上述特征，极易使人想到智能算法中源于人工神经网络的深度学习模型[8]。【切入点】但迄今深度学习模型需要海量的训练样本量，因为样本量不足时深度学习模型的精度显著低于其他智能算法[9]。而需要少量样本即能建立目标变量与原因变量或特征变量的智能算法，例如随机森林模型和支持向量机模型，前者难适用于特征变量间存在某些相关或同一特征变量具有显著空间分布或变异性的情景，而支持向量机无法有效应对强非线性问题。【拟解决的关键问题】为此，本文基于安徽淠史杭灌区瓦西干渠灌域内在时间上严格匹配的用水调度目标流量和特征变量的观测数据，拟通过融合随机森林法和SHAP方法2种算法，来应对上述灌区用水调度具备的特征，由此建立灌区用水调度目标流量与各影响特征变量之间的非线性映射定量表征，给出简洁实用的特征变量组合，同时得到各特征变量对目标流量的影响程度及影响方向，为改进当前灌区用水调度仅凭经验定性决策的现实状况提供定量支撑。

1 材料与方法

1.1 研究区域概况

淠史杭灌区位于安徽六安，始建于1958年，包括淠河、史河和杭埠河3个子灌区，实际灌溉面积约67万hm2，是以防洪、灌溉、供水为主，兼有发电、生态、旅游等功能的综合性水利工程，是典型的引、蓄、提3种水源综合利用灌区[10]。本文关注的瓦西干渠位于淠河子灌区上段（图1），渠首瓦西干渠进水闸的设计流量为27.4 m3/s，干渠长61.2 km，其包括15条支渠，涉及灌溉面积约3.84万hm2。

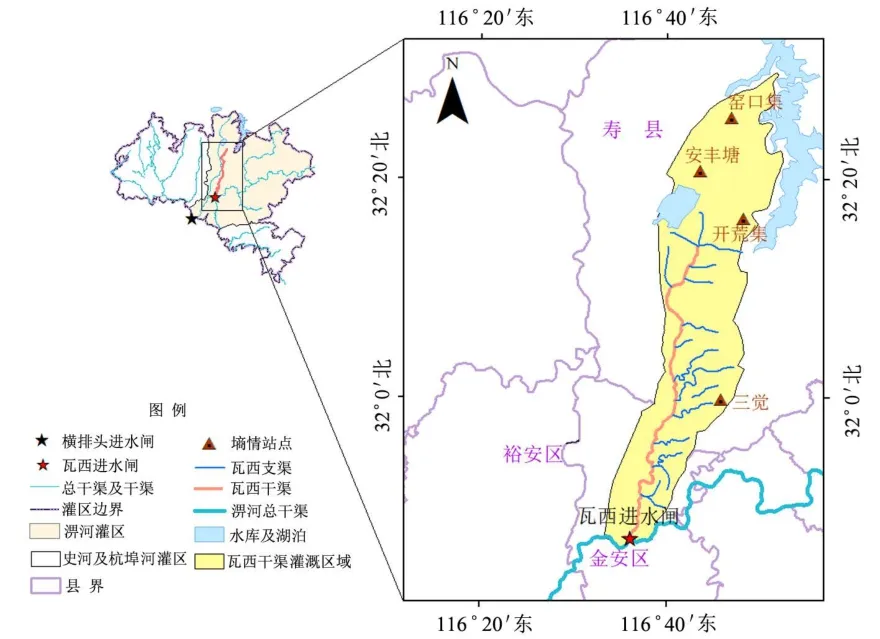
图1 淠史杭灌区瓦西干渠灌域示意Fig.1 Schematic diagram of Waxi canal irrigation area in Pishihang Irrigation District

1.2 特征变量与观测数据

灌区用水调度的目标变量是瓦西干渠进水闸（后文简称瓦西进水闸）的实时调度流量（Q）。依据以往经验，影响目标流量的原因或特征变量共有8类，如表1所示。温度、降雨、土壤墒情等数据具有显著的空间变异性，为定量表征局部小气候或水文水力特征，故把各个观测点获得的实测数据单独作为特征变量，以反映其对目标变量的真实影响，由此形成8类共87个特征变量。

基于特征变量和目标变量这2类因果数据在时间上匹配的原则，收集淠史杭灌区瓦西干渠灌域内的上述变量数据，为建立目标变量和特征变量之间的非线性定量映射表征提供基础数据。其中，淠史杭灌区瓦西干渠进水闸用水调度流量记录、用水调度请求、中小型水库和塘坝蓄水量以及城市和生态分阶段供水补水水量数据均来自淠史杭灌区管理总局。用水调度请求的原始数据为地方向调度总局发送的调度请求电报，由于部分电报没有具体流量值，故用0、1、2来表征无电报、电报要求减少流量和电报要求增加流量这3种情况。如图1所示，从淠河渠首横排头到瓦西灌域，渠道共经过了六安市的裕安区、金安区和淮南市的寿县，为确保模型模拟的精度，搜集了这3个区县内共60个雨量站点的日降雨数据，以考虑瓦西进水闸上游及干渠控制范围内降雨对渠道流量的影响。墒情数据和日降雨量数据来自六安市水文水资源局。灌期经验划分和淠史杭灌区温度日变化数据也均为特征变量数据，灌期和非灌期分别用0和1定量表征。气温数据以及长系列降雨数据（1996—2020年）来自中国气象科学数据共享服务网的《中国地面气象资料数据集（V3.0）》。气温数据提取2018—2020年的逐日气象观测资料。各特征变量及说明汇总至表1。

表1 特征变量及说明Table 1 Characteristic variables and their description

1.3 非线性映射定量表征方法

为消除该非线性映射中不同特征变量之间和考虑空间变异时同类特征变量之间的相关冗余、提高对灌区用水调度经验描述的精度，采用沙普利可加性特征解释法（Shapley Additive exPlanations，SHAP），简称SHAP方法，进一步优化该非线性映射的具体表达，计算出各特征变量对用水调度目标流量的重要性赋分及排序，从而表征各特征变量对调度流量的影响程度及影响方式。

1.3.1 基于随机森林模型的非线性回归映射

随机森林模型是以树状网络的形式，形成灌区用水调度目标流量与各特征变量之间的非线性回归映射。该映射基于所有与灌区用水调度相关的特征变量作为样本集，在特定规则下形成决策树节点与目标变量之间的树状决策（即决策树），再由众多决策树形成决策森林网络。模型构建过程中需根据预测结果不断优化特征变量数目和决策树数目，最终即可得到灌区用水调度目标流量与各特征变量之间的非线性回归映射。在决策树形成过程中未被抽到的样本数据称为袋外数据（out-of-bag，OOB），其可用来估计内部误差和评价特征变量重要性[11-12]。

1.3.2 特征变量重要性评价方法的选择

表2为不同类型特征变量之间的相关性系数矩阵。由表2可知，特征变量之间的相关性不仅存在于同类型特征变量之内，也存在于不同类型特征之间，即最终选定的不同调度情景下的特征变量组合，特征变量间一定存在较大的相关性，这与选择特征时要使特征变量之间相关性最小的原则不相符[13]，会造成随机森林模型预测结果的误差。另外，通过袋外数据误差来衡量特征变量重要性的方法，存在可解释性弱等问题。故本文最终选用能克服上述问题的SHAP方法来定量评价各特征变量对目标流量的重要性，并优化掉多余的特征变量相关[14]。

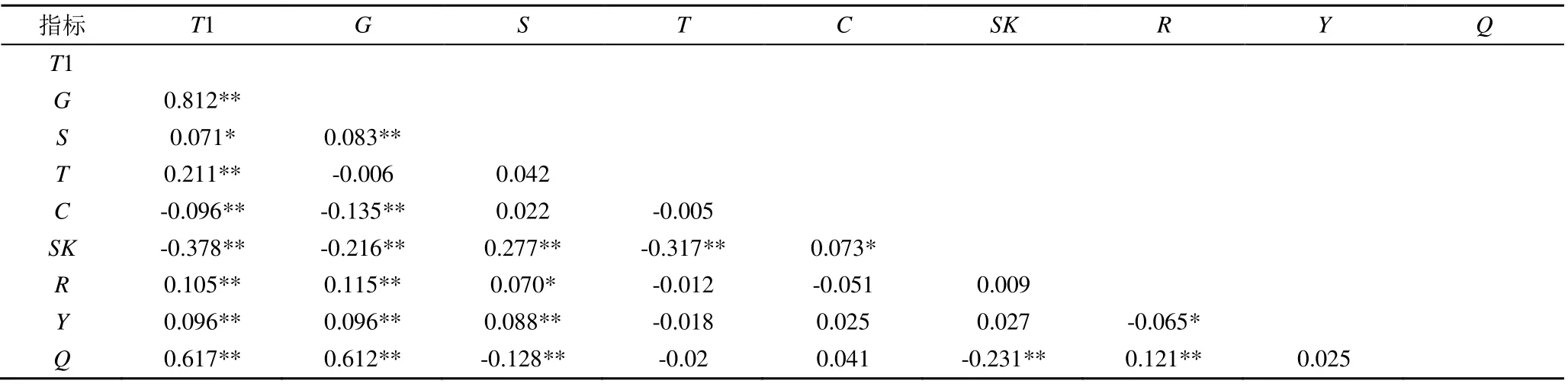
表2 特征变量相关系数矩阵Table 2 Pearson correlation coefficient matrix of Characteristic variables

注*，plt;0.05；**，plt;0.01。

1.3.3 SHAP方法

灌区用水调度过程中，针对目标流量，管理人员事实上在不断权衡各影响要素或特征变量的重要程度，进而动态联合决策，这是一个典型的各特征变量之间的合作博弈过程。在合作博弈中，各特征变量的Shapley值兼具了效率和公平的原则，而SHAP值则是合作博弈中的最佳Shapley值，直接反映了特征变量的重要程度[15]。

实际应用中，SHAP值计算为：

特征变量的Shapley值是所有可能特征变量组合对目标结果贡献的加权求和：

每一个数据样本对应的预测值，都可得到一个SHAP值，即将式（2）代入式（1）后可求得，其绝对值反应的就是该特征的影响力大小。而特征变量的重要性赋分为所有SHAP值绝对值的平均值。本文用Python带有的Shap库来计算各特征变量的重要性赋分。

1.4 模型精度评价指标与特征变量筛选准则

采用五折交叉法来验证上述非线性映射的预测值与实测值之间的吻合程度[16]，定量评价指标包括决定性系数（coefficient of determination，R2）和平均绝对误差（mean absolute error，MAE）。特征变量往往较多，故需筛选出主要特征变量，形成简洁实用的特征变量组合，为此，选取重要性赋分归一化后累计达到85%的特征变量。

2 结果与分析

2.1 特征变量重要性评价分析

由长系列降雨数据分析可确认2018—2020年分属为3种不同的旱涝等级年型。为此，分别开展长时间整体序列和典型年的特征变量重要性评价，依据模拟值与观测数据之间的拟合度，来选取适宜的样本类型，给出更切实际的灌区用水调度建议。限于从六安市60个气象站点所能获取的降雨数据历史年限限制，2018—2020年旱涝等级由中国气象科学数据共享服务网所获长系列（1996—2020年）降雨数据来确定。

2.1.1 长时间整体序列样本分析

将2018—2020年与淠史杭灌区瓦西干渠用水调度历史事件相关的8类、87个特征变量全部输入随机森林模型，经测试评估调参后，MAE约为1 572.70 mm，R2约为0.806 8。在此基础上，由SHAP方法获得了各特征变量的SHAP值。为了尽可能展示更多的特征变量及重要性赋分，图2给出了重要性赋分大于0.001的31个特征变量及其排序。由图2可知，最应关注的特征变量是能表征灌域陆面小气候状态的温度（T1），这与陆面温度直接决定着作物生长密切相关。其次应关注的特征变量是灌期经验划分和小（二）型水库蓄水量。第3～第6个应关注的特征变量分别是中型水库蓄水量、时间及城市和生态分阶段供水补水水量。通常而言，降雨和调水请求亦应重点关注，但其特征变量重要性赋分却显著靠后，原因是降雨直接补给了水库和灌域土壤（墒情），故不是影响用水调度流量的直接要素，而调水请求仅是用水单元的需水总量，不能与总闸的用水调度流量在以天为单位的细分时空分布上相匹配，故亦属于间接影响要素。

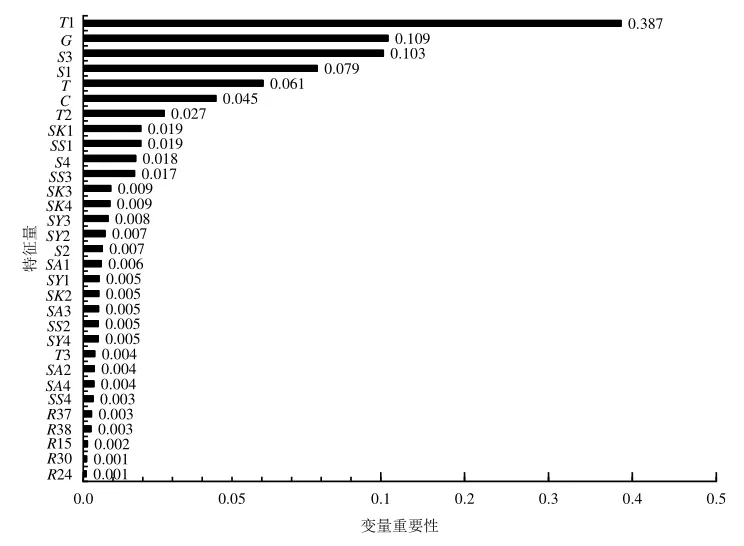
图2 重要性得分大于0.01的31个特征变量及排序Fig.2 31 characteristic variables with significance score greater than 0.01 and their ranking

2.1.2 典型年样本分析

通过对长系列降雨数据的分析后可获知，2018—2020年累计降雨量分别为1 316.53、620.73、152.70 mm，每年累积降雨量的降雨距平分别为24.70%、-41.20%、48.97%，基于以降雨距平百分数（Pr）为指标的旱涝划分体系可知[17]，瓦西干渠灌域在2018年是正常年，2019年为偏旱年，2020年为偏涝年。

将这3个典型年的用水调度样本数据分别导入模型，特征变量仍是87个，调参后，模型输出如下：2018年的MAE为2.09，R2为0.7741；2019年的MAE为0.91，R2为0.84；2020年的MAE为1.96，R2为0.77。特征变量重要性赋分中，有25个特征变量排序一直稳居在前30，结合前述长时间整体序列样本的重要性赋分及排序，图3直观给出了这25个特征的重要性赋分及排序。图3中从左往右为长时间序列下特征变量重要性赋分从高到低排序。由图3可知，3个典型年都应重点关注的特征变量，是时间以及能表征灌域陆面小气候状态的温度。偏涝（2020年）时，中型水库蓄水量重要性位于第二，降雨的重要性相较正常年和偏旱年显著提升（2020年降雨重要性排名进入了前30），而灌期经验划分及用水调度请求的重要性显著下降。偏旱（2019年）时，灌期经验划分、城市及生态用水量、用水调度请求排名相较其他2个典型年显著提升，土壤墒情亦有提升。另外，中小型水库蓄水量的重要性比其他2个典型年有所下降。正常年（2018年）时，塘坝蓄水量的重要性比较突出，分析其原因是瓦西灌域内优先利用当地塘坝蓄水资源，若其蓄水量减小，则渠道用水会对其进行补充。

2.1.3 两类样本综合对比分析

长时间整体序列的各特征变量重要性排序和正常年（2018年）结果相近，这表明长时间整体序列确实会弱化特殊典型年情景。另外，降雨和用水调度请求在长时间整体序列样本和正常年样本中的重要性排名不高，但在偏涝年和偏旱年这类非常规调度样本情境下的重要性开始凸显。由此可见，在长时间整体序列样本中有效融入特殊典型年情景，是提高模型结果应用性的重要手段。

对于降雨而言，偏涝年（2020年）和偏旱年（2019）这类需非常规用水调度的特殊年份，应重点关注瓦西干渠沿程，尤其中下游的降雨（站点）；而长时间整体序列和正常年（2018年）这类常规用水调度年份，则应重点关注瓦西干渠进水闸上游的降雨（站点）。分析其原因是，偏旱年或偏涝年时灌区用水调度多关注灌域内的降雨，且瓦西干渠中下游更易发生旱涝灾害；若降雨正常，则会弱化瓦西干渠灌域内降雨的重要性，因为此时水源多来自淠河的正常来水。对于水库及塘坝蓄水量而言，任何数据序列样本下中型水库蓄水量都比较重要性，而偏涝年和偏旱年这类特殊场景下小型水库和塘坝蓄水量的作用尤其突出。对于土壤墒情而言，无论何种数据序列样本，瓦西干渠中后段土壤墒情（开荒集）都应重点关注。

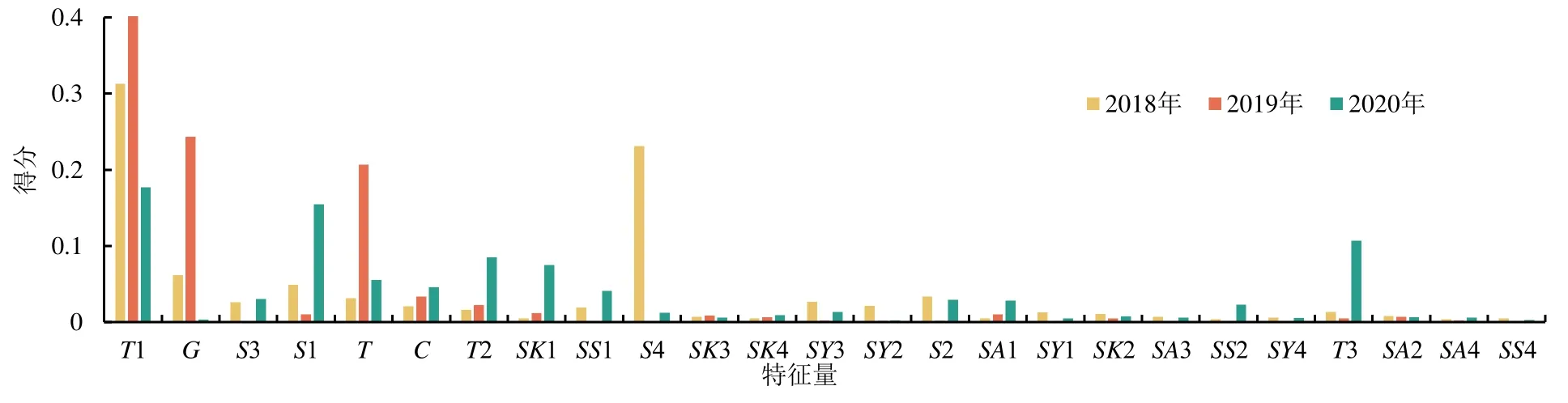
图3 不同典型年特征变量赋分变化情况Fig.3 Variation of characteristic variable scores in different typical years

2.2 特征变量组合

不同特征变量组合及精度评价指标值如表3。由表3中前6组模拟结果可知，合理的特征变量组合是重要性赋分累计达到85%的前9个特征变量，因为更少和更多的特征变量会削弱模型预测精度。为验证更多特征变量组合的模拟精度，表3中第7～第12个特征变量组合是剔除9个特征变量中（考虑空间变异时）同类变量的结果，由其评价指标值可见，仅剔除T2（表征水库附近小气候的温度）时模型检验结果最优（即第9个特征变量组合）。在基于组合9所得结果最优的前提下，组合13—组合18检验了不同用水调度情境下特征变量组合得到的模型预测精度值。根据不同用水调度情景，将偏涝年（2020年）和偏旱年（2019年）降雨重要性赋分都相对较高的R37站点考虑在内，组合13—组合15模拟不考虑为城市和生态供水补水时，将降雨以及用水请求电报考虑在内的用水调度情景；组合9以及组合16—组合17则是对应的考虑为城市和生态供水补水时的用水调度情景。组合18是将正常年（2018年）重要性赋分较为突出的塘坝蓄水量考虑在内的用水调度情景。同最初利用87个特征量训练模型相比较（R2为0.806 8），除了组合5和组合6，其他特征变量组合得到的模型精度R2均显著提高，且最佳特征变量组合是组合9。

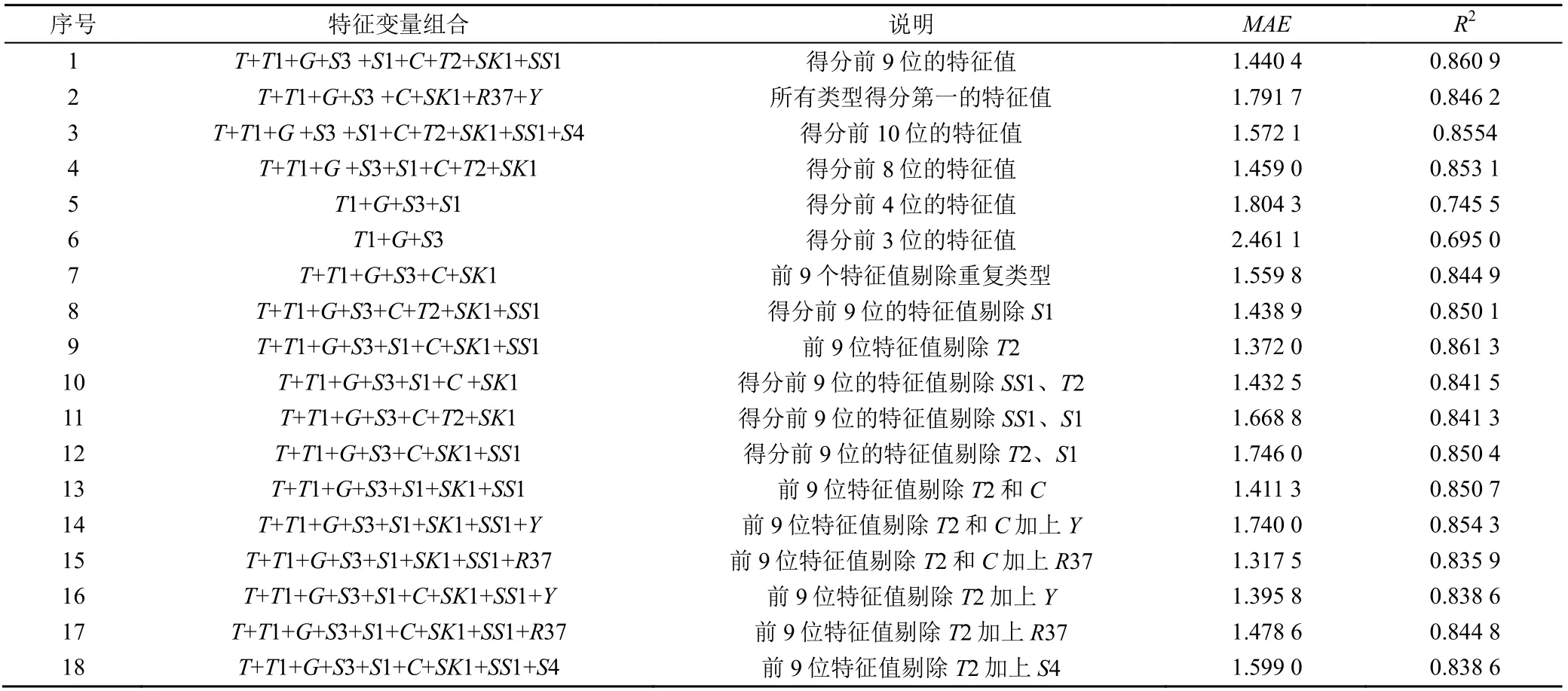
表3 不同特征变量组合的模型预测精度Table 3 Model prediction accuracy of different combination of characteristic variables

2.3 特征变量影响目标变量的方向性

图4定量表征了各特征变量对用水调度目标流量影响的正负性。图4中每行代表1个特征变量，横坐标为其SHAP值，1个点代表1个样本。颜色越红说明特征本身数值越大，颜色越蓝说明特征本身数值越小。SHAP值大于0时正向影响目标流量，即此时应调大流量；若SHAP值小于0则调小流量。从其SHAP值分布可知，降雨（位于瓦西干渠进水闸上游的观测点R37）双向影响用水调度目标流量，这与灌区需充分利用雨洪水资源密切相关。降雨正向影响用水调度目标流量时，瓦西干渠进水闸上游来水多是雨洪水源，负向影响时则是瓦西干渠上游主干渠引来的淠河日常来水。另外，由图4可知，其分布在SHAP值正半轴样本点更多、且SHAP值绝对值明显更大，这表明瓦西进水闸调度时，在确保不发生洪涝灾害前提下，降雨应尽量保留在渠系中，形成渠池水资源，达到最大节约用水的目标。结合所有特征量的SHAP值分布可知，全年大部分时间内瓦西干渠进水闸都处于关闭状态，故其大量样本点集中在一固定值附近且位于坐标轴的左半部分。温度较高时，瓦西进水闸调度流量通常是增大的。与此同时，水库蓄水量与用水调度流量基本呈负相关，这表明蓄水量与瓦西干渠进水闸过流量之间具有互补效应。另外，灌期经验划分、城市和生态供水补水水量与用水调度流量正相关，土壤墒情与用水调度流量负相关，这符合正常的灌区用水规律。

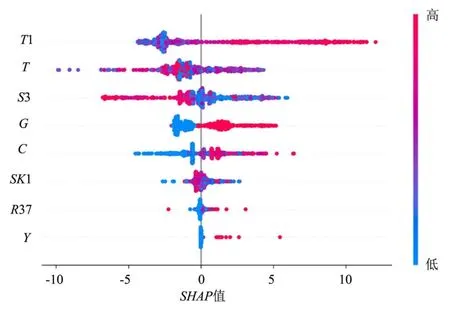
图4 SHAP 分析的变量散点Fig.4 Scatter plots of variables for SHAP analysis

3 讨 论

李刚军等[18]基于事理推理技术将灌区水量调度事件作为历史事件构建事件库，采用在事例库中寻找相似案例的方法来应对灌区水量调度的复杂性和不确定性。此方法要解决的问题与本文一致，且也同样是将人工智能技术应用到解决灌区调度问题中来。但其与本文侧重点有所不同，相似事例虽能提供给调度员一定参考信息，但调度指令的下达仍然需要以适用于不同实际调度情景的经验为主。但若能实现2个方法的相互补充，即可更好的应对用水调度问题的复杂性和不确定性。

同时本方法还有如下可改进的方面：首先，2018—2020年的淠史杭灌区用水调度历史事件数据可代表日常、抗旱和防涝调度3种不同典型灌区用水调度情形，故具有一定的普适性。然而，灌区实际用水调度具有随机性，这归因于自然和社会影响要素的多变性和不确定性。故后续将增加更多的年度样本数据，并对特殊场景进行聚类分析等特殊化处理，以增加模型的普适性和合理性。其次，为提高模型精度，在增加年度样本数据基础上，应引入作物生长周期、灌溉周期等更多的特征变量，进一步细化灌区用水调度过程，以期能使模型细分出更加精准的灌区用水场景。与此同时，应增强实测数据精度。目前有2个因素影响实测数据精度，一是淠史杭灌区已有用水调度数据多以人工测量、手工书写方式进行记录，二是灌区内小型水库塘坝蓄水量和土壤墒情等数据非逐日记录，而当前开始实施的数字灌区项目将在一定程度上弥补该问题。

随着实测样本数据的增加，事实上深度学习模型比随机森林模型等智能算法更具精细预测未来场景的能力，但其前提是极其海量丰富的大数据样本，否则深度学习的细分、识别和预测场景的能力劣于随机森林等模型[9]。故与灌区合作开展更加丰富精准的数据搜集、并深度发掘已有历史数据，同时结合数值模拟仿真结果，是建立更加强大的灌区用水调度模型的必由之路。

4 结 论

1）偏涝年时中型水库蓄水量和降雨重要性相较正常年和偏旱年显著提升，而灌期经验划分及用水调度请求重要性显著下降；偏旱年时，灌期经验划分、城市及生态用水量、用水调度请求的重要性相较偏涝年和正常年显著提升，水库蓄水量重要性有所下降，降雨重要性也显著下降。瓦西干渠中后段区域的土壤墒情是重要的用水调度参考指标。偏涝年时灌区用水调度参考的降雨站点多位于瓦西干渠中下游，正常年时多位于瓦西干渠进水闸上游。中型水库蓄水量在偏旱年和偏涝年时重要性尤为突出，而正常年时小型水库及塘坝的蓄水量对用水调度影响更大。

2）瓦西干渠进水闸用水调度的最优特征变量组合是：时间+（表征陆面小气候的）温度+灌期经验划分+小（二）型及中型水库蓄水量+城市和生态分阶段供水补水水量+干渠中下游土壤墒情（开荒集和三觉土壤墒情观测站）。

3）蓄水量与瓦西干渠进水闸过闸流量之间具有互补效应；降雨双向影响用水调度目标流量，且在确保无洪涝灾害时应尽量利用降雨水资源。

[1]柴福鑫, 邱林, 谢新民. 灌区水资源实时优化调度[J]. 水利学报, 2007,38(6): 710-716.

CHAI Fuxin, QIU Lin, XIE Xinmin. Real time optimal dispatch of water resources for irrigation area[J]. Journal of Hydraulic Engineering,2007, 38(6): 710-716.

[2]GHAHRAMAN Bijan, SEPASKHAH Ali-Reza. Optimal allocation of water from a single purpose reservoir to an irrigation project with pre-determined multiple cropping patterns[J]. Irrigation Science,2002, 21(3): 127-137.

[3]YANG Ling, QIU Yuanmei, ZHANG Huiying, et al. The study of decision support system on water resources optimal allocation in irrigation area based on unsufficient irrigation[J]. Water Saving Irrigation, 2012, 345: 716-725.

[4]邵东国, 吴振, 顾文权, 等. 基于供求关系和生产函数的灌区水量使用权交易模型[J]. 水利学报, 2017, 48(1): 61-69.

SHAO Dongguo, WU Zhen, GU Wenquan, et al. Water use right trading model of irrigation area based on supply-demand relation and production function[J]. Journal of Hydraulic Engineering, 2017, 48(1): 61-69.

[5] WANG Xuemei, LEI Xiaohui, GUO Xuning, et al. Forecast of irrigation water demand considering multiple factors[C]. Beijing: Remote Sensing and GIS for Hydrology and Water Resources, 2015.

[6] 许冲, 戴福初, 姚鑫, 等. 基于GIS与确定性系数分析方法的汶川地震滑坡易发性评价[J]. 工程地质学报, 2010, 18(1): 15-26.

XU Chong, DAI Fuchu, YAO Xin, et al. GIS platform and certainty factor analysis method based wenchuan earthquake-induced landslide susceptibility evaluation[J]. Journal of Engineering Geology, 2010,18(1): 15-26.

[7] 徐艳琴, 白淑英, 徐永明. 基于两种方法的攀西泥石流易发性评价对比分析[J]. 水土保持研究, 2018, 25(3): 285-291.

XU Yanqin, BAI Shuying, XU Yongming. comparative analysis of debris flow susceptibility assessment based on two methods in pani district[J].Research of Soil and Water Conservation, 2018, 25(3): 285-291.

[8] GOODFELLOW Ian, BENGIO Yoshua, COURVILLE Aaron. Deep learning[M]. Cambridge: Massachusetts Institute of Technology press, 2016.

[9] 史良胜, 查元源, 胡小龙, 等. 智慧灌区的架构、理论和方法之初探[J].水利学报, 2020, 51(10): 1 212-1 222.

SHI Liangsheng, ZHA Yuanyuan, HU Xiaolong, et al. A preliminary exploration of framework, theory and method for intelligent irrigation district[J]. Journal of Hydraulic Engineering, 2020, 51(10): 1 212-1 222.

[10] 朱红. 淠史杭灌区水资源配置与调度实践[J]. 中国水利, 2019(3): 16-18.ZHU Hong. Water allocation and regulation in Pishihang Irrigation District[J]. China Water Resources, 2019(3): 16-18.

[11] BREIMAN LI, FRIEDMAN Jerome H, OLSHEN RA, et al. Classification and regression trees (CART)[J]. Biometrics, 1984, 40(3): 358.

[12] BERK Richard A. Classification and Regression Trees (CART)[M].New York: Springer, 2016.

[13] PENG Hanchuan, LONG Fuhui, DING C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis amp; Machine Intelligence, 2005, 27(8): 1 226-1 238.

[14] 宋亚男, 武惠韬, 应俊, 等. 基于机器学习算法探讨糖尿病视网膜病变的风险因素[J]. 解放军医学院学报, 2021, 42(9): 906-912, 992.

SONG Ya’nan, WU Huitao, YING Jun, et al. Risk factors analysis of diabetic retinopathy based on machine learning[J]. Academic Journal of Chinese PLA Medical School, 2021, 42(9): 906-912, 992.

[15] LUNDBERG Scott M, ERION Gabriel G, LEE Su-in. Consistent Individualized Feature attribution for tree ensembles[J]. Computer Science, 2018, 3: 1 706.

[16] 杨柳, 王钰. 泛化误差的各种交叉验证估计方法综述[J]. 计算机应用研, 2015, 32(5): 1 287-1 290, 1 297.

YANG Liu, WANG Yu. Survey for various cross-validation estimators of generalization error[J]. Application Research of Computers, 2015,32(5): 1 287-1 290, 1 297.

[17] 陆桂荣, 郑美琴, 袁安芳, 等. 日照市旱涝变化特征分析[J]. 中国农业气象, 2009, 30(3): 436-439, 448.

LU Guirong, ZHENG Meiqin, YUAN Anfang, et al. Characteristic of flood and drought changes in Rizhao city[J]. Chinese Journal of Agrometeorology, 2009, 30(3): 436-439, 448.

[18] 李刚军, 罗军刚, 解建仓, 等. 基于事例推理技术在灌区水量调度中的应用[J]. 西安建筑科技大学学报(自然科学版), 2008, 40(1): 126-131.

LI Gangjun, LUO Jungang, XIE Jiancang, et al. Research on case-based reasoning for water dispatching of irrigation region[J]. Journal of Xi’an University of Architecture amp; Technology (Natural Science Edition),2008, 40(1): 126-131.

Water Allocations in Irrigation Districts Determined by Random Forest Combined with SHAP Method

SU Nan1, ZHANG Shaohui1,2*, BAI Meijian1,2, ZHANG Baozhong1,2
(1. China Institute of Water Resources and Hydropower Research, Beijing 100038, China;2. State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, Beijing 100038, China)

【Objective】Decades of management of various irrigation districts have accumulated valuable experiences, but how to make most of these experiences has not yet been appreciated. The purpose of this paper is to fill this gap, proposing a method to harness these experiences to improve water allocation calculation in irrigation districts.【Method】The analysis is based on data measured over a three-year period from an irrigation area at the Waxi branch in the Pishihang irrigation district. We consider spatial variation in variables such as temperature,rainfall and soil moisture in integrating the interpretation method of the random forest model with the SHAP model.Nonlinear quantitative relationship between the target water allocation and each variable was constructed using limited data samples.【Result】The model obtains the important scores and changes in each variable in a long time series for different typical years. In addition to the combination of characteristic variables suitable for actual water dispatching, the indexes of characteristic variables that dispatchers mainly refer to different dispatching scenarios can be analyzed and obtained. Combined with the analysis ofSHAPvalue, the positive and negative directions of the response of water dispatching target flow to each characteristic variable is obtained.【Conclusion】The method proposed has realized quantitative representation of historical experience of water dispatching in irrigated areas and provided guidelines for rational prediction of different water dispatching flows in irrigation districts.

Pishihang irrigation district; water dispatching; random forest model; SHAP method; characteristic variable; nonlinear characterization

苏楠, 章少辉, 白美健, 等. 融合随机森林和SHAP方法的灌区用水调度经验分析：以淠史杭灌区瓦西干渠灌域为例[J].灌溉排水学报, 2022, 41(11): 122-128.

SU Nan, ZHANG Shaohui, BAI Meijian, et al. Water Allocations in Irrigation Districts Determined by Random Forest Combined with SHAP Method[J]. Journal of Irrigation and Drainage, 2022, 41(11): 122-128.

S274

A

10.13522/j.cnki.ggps.2022123

1672 - 3317（2022）11 - 0122 - 07

2022-03-10

中国水利水电科学研究院专项项目（ID0145B052021）

苏楠（1997-），女，云南楚雄人。硕士研究生，主要从事灌区用水管理研究。E-mail: Sue_sn_email@163.com

章少辉（1977-），男，河北石家庄人。教授级高级工程师，博士，主要从事水动力学模拟与灌区用水调控研究。E-mail: zhangsh@iwhr.com

责任编辑：白芳芳