电阻的等效分解及其在电路分析中的应用
秦章蓓
(西南民族大学,四川 成都 610225)
电路分析中常用的工作方法即为电阻等效分解法,对于简单的串并联电路、复杂的混联电路以及含有受控源的二端网络等各类电路,均可以采用适当的方式将电路电阻快速等效分析,实现对相关电路参数的快速计算。本文主要提出了一种假设节点N的电路电阻等效方法,并针对性地进行了论证分析,同时针对二端网络提出了受控源电路和无受控源混联电路的分析方法,各类方法的论述均附有相关案例,能够有效为相关人员提供指导。
1 等效分解原理分析
某电路中电阻的等效分解如图1所示。该电路具有3个节点,分别为a、b、c,这里应用、与表示3个节点的电压。其中,电阻支路即为ab,电阻阻值为R,通过等效分解的方式可以得到图1(b)所示电路,电阻分为αR与(1-α) R两部分,两电阻相互串联,此时的节点N可以处于任意位置,即N的电压不确定。如果设节点c的电压即为节点N的电压,则此时两节点重合,此时的α数值为:

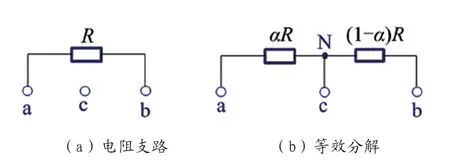
图1 电阻的等效分解
根据式(1)可以求得:
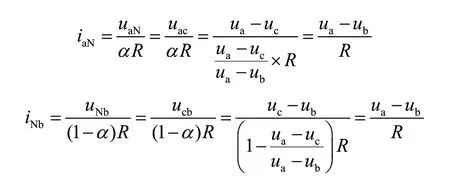
由于iaN= iNb,则iNc= 0
由此可见,Nc支路并无电流流通,可以假设该回路为断路,同时ab两端之间的等效电阻数值为R,证明图1(b)可以作为图1(a)的等效电路。因为c节点为任意节点,因此在应用该方法进行电阻等效分解的过程中,可以在任意节点转移电阻支路,且其他的支路电流与电压并不会因此受到影响。
2 二端网络等效电阻的快速求解方法
2.1 含有受控源电路等效电阻的分析
外加电源法的长远的等效电阻求解方法之一,为验证外加电源法的应用效果,本文选择针对图2(a)所示电路应用外加电压源的方法进行等效分析。
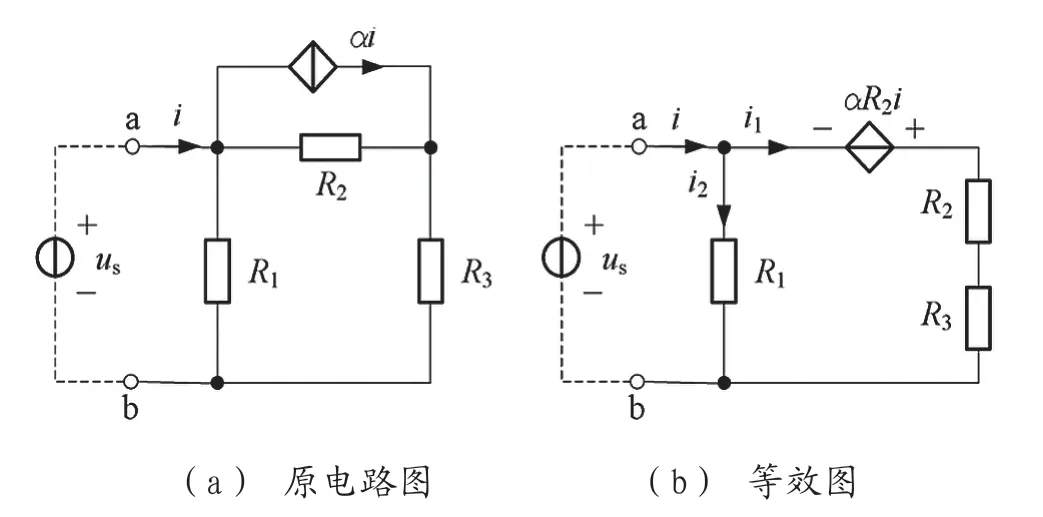
图2 含有受控源的二端网络
对于图2(a)中的电流源,图2(b)等效图中将其转化为电压源,根据基尔霍夫电压定律可以求得:

根据基尔霍夫电流定律,得到下式:

联立以上3式可得:

相对而言,上述电路结构的难度不高,通过3组公式即可完成等效电阻的求解工作,然而在复杂电路之中,外加电压求解的难度将大幅度提升,大量的方程公式将大幅度增加计算时长,下面针对受控源电路提出更简单的电阻等效求解方法。
2.2 二端网络中的受控源电路模型的分析
受控电源通常不被认为是独立电源,当电路中存在受控电源时,电阻电路的等效变换无法直接变换出等效电阻。通过深入分析受控电源电路发现,此类电路在等效电阻计算过程中具有一定的规律。通过提取电路中的受控电源相关内容,对其结构进行完全分解,并针对电压源与电流源两种受控电源进行分别研究,具体如下。
2.2.1 受控电流源结构
图3所示电路为含有受控电流源的二端电路,图中的N即为单纯的电阻网络,在等效电阻求解过程中可以借助外加电压源法,得到公式如下:

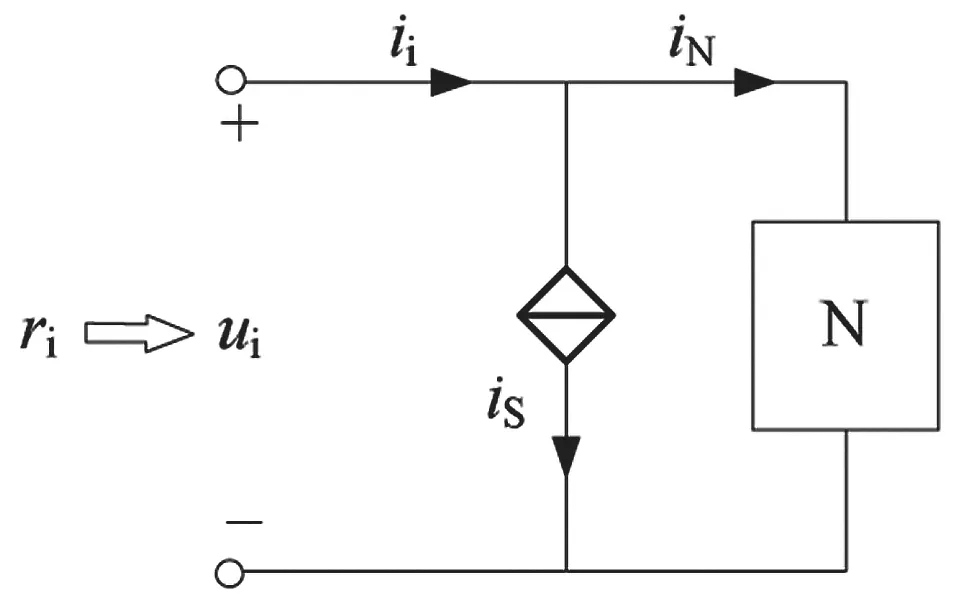
图3 受控电流源基本结构
ri的计算结果表明,图3电路电阻等效后得到的数值为RN这一并联电路网络阻值的iN/(iS+ iN)倍,即电阻网络所在支路电流与总电流之间的比值。在计算分析阶段,总电流ii需要保持与两支路电流相同的参考方向,如图3所示。按照上述方法计算求得的电阻数值可能为负,负值电阻证明此处的电路为电源。
2.2.2 受控电压源结构
图3所示电路为含有受控电压源的二端电路,图中的N即为单纯的电阻网络,在等效电阻求解过程中可以借助外加电压源法,得到公式如下:

ri的计算结果表明,图4电路电阻等效后得到的数值为RN这一串联电路网络阻值的ui/uN倍,即总电压与电阻网络两端电压之间的比值。在计算分析阶段,总电压ui需要保持与各分电压相同的参考方向,如图4所示。上述计算结果表明,当二端电路中存在受控电源时,将某个折算系数与电阻网络的电阻数值相乘即可得到等效电阻的数值,在掌握具体系数数值的情况下,即可实现对电路电阻的等效分解,最终得到一个较为简单的纯电阻电路,有效降低电路分析的 难度。

图4 受控电压源基本结构
3 无源二端网络混联电路等效电阻电路分析
上文主要对二端网络中含有受控电源的情况进行了分析,当二端网络中不存在受控电源时,等效电阻的分解计算难度相对较低。因此,本文对于二端网络中的并联与串联电路不再赘述,主要针对相对复杂的混联电路进行研究分析,分析处理混联电路的具体方法,为相关电路的等效电阻分解与电路分析提供参考。
拆点分线法是直流电路等效处理过程中的常用方法,该方法不会对电路结构进行修改,处理方法相对直观明了。在实际应用过程中,计算人员需要确认二端无源混联电路中可合并节点的数量,当数量不低于2个时,则可以应用该方法。对于存在两个可合并节点的电路,处理过程中需要将一条导线设置在节点旁边,并将其中一点拆分,形成双节点回路。此时,计算人员能够更简单地完成对混联电路各组成电流的判断分析工作,而且现有的电路结构不会产生较大的变化,该方法实质上是从局部到整体的等效电阻分解计算方法。
某无源二端混联电路如图5(左)所示,该电路中串并联的电阻多且复杂,但在实际计算分析过程中可以针对c与c’这两个能够合并的节点应用拆点分线画法进行处理,通过添加导向的方式将节点分开,得到图5(右)所示单路,此时的R3与R6可以视为一组并联的电阻,两个并联电阻又与R1串联,串联后的电阻则与R2并联,依此类推,最终实现对电阻的等效求解。

图5 混联电路示意图
当无源二端混联电路中能够合并的节点数量超出2个时,则可以针对相应节点进行添加导线划分节点的方式处理,最终快速实现对混联电路的分解与等效分析计算。
4 结语
综上所述,电阻等效分解法对于解决复杂的电路分析问题具有重要作用,本文提出了定义节点简化电路的电阻等效分解方法能够有效处理复杂电路分析问题,在密勒定理求证、非平衡桥式电路分析以及T 形反馈放大器分析中的分析求解难度较低,能够更高效地完成电路分析工作;二端网络受控电源电路等效分析过程中需要结合电压源、电流源具体情况进行置零处理,当受控电源数量较多时需要进行合并或分层计算;二端无源网络中的混联电路分析过程中可以采用拆点分线等效处理,实现对电路的快速分析。

