基于Lévy稳定分布的失效概率预测模型
黄啸宇,顾冲时,何 菁
(1.河海大学水利水电学院,江苏 南京 210024;2.南京市水利建筑工程检测中心有限公司,江苏 南京 210036)
失效概率是定量估计工程结构可靠性的重要指标。一般来说,失效概率值很小,并且受各影响因素统计分布的选取影响很大,极为敏感[1-2]。合理选择随机变量的统计分布是有效计算失效概率的前提。目前描述随机变量的统计分布有正态分布、对数正态分布、极值分布等,然而这些统计分布并不能准确描述出某些随机变量的尖峰与拖尾特征。而Lévy稳定分布是分数阶统计分布的一种,也属于幂律分布,常用于描述服从非高斯分布的随机变量,并且可以刻画出随机变量尖峰、拖尾及非对称的特征[3]。随着计算机科学的迅速发展,前人在已有理论和算法的基础上,开发了一系列易用的Matlab软件包来解决估计Lévy稳定分布的参数、生成随机数、拟合图像等相关问题,使得Lévy稳定分布在数值模拟和统计上更加备受关注。
本文以内蒙古永济第二节制闸为例,通过Lévy稳定分布描述各随机变量的统计特征,建立极限状态方程,计算结构的失效概率。
1 Lévy稳定分布的统计基础
1.1 Lévy稳定分布的统计特征
Lévy稳定分布是一类广泛应用于反常扩散、信号处理和金融工程等领域的统计分布[4]。近年来,许多学者对Lévy稳定分布理论和应用进行了深入研究,并取得了一定成果。目前使用特征函数来描述Lévy稳定分布是比较简单的[4-5]。
在理论应用上,Samorodnitsky和Taqqu提出,假设随机变量X服从Lévy稳定分布,即X~S0(α,β,γ,δ),那么X的特征函数
(1)
式中,α、β、γ、δ分别为稳定指数、倾斜指数、尺度参数和位置参数,参数的取值范围为, 0≤α≤2,-1≤β≤1,γ>0,δ∈R,其中,α的值分别为1和2时10-3,对应的是Lévy稳定分布的特殊情况,即柯西分布和高斯分布;signt为t的符号函数;i为1,2,3,4,…,t为步长。
1.2 Lévy稳定分布的优势
确定影响结构可靠性的随机变量的统计分布是准确评估水工结构可靠性的前提,《水利水电工程钢闸门设计规范》指出,作用在闸门上的荷载主要有静水压力、动水压力、自重等,这些荷载都可以作为随机变量进行失效概率的计算。目前应用于工程结构随机变量估计的常用统计分布有正态分布、对数正态分布、极值I型分布、威布尔分布等。然而,这些统计分布只通过观测试验资料的期望和方差来确定工程随机变量的分布,却忽视了偏态、峰态、尾部等信息,尤其不能准确描述随机变量概率密度函数的尖峰及尾部的幂律特征,因而不能全面真实地反映服役水工结构的可靠性等信息,甚至可能得出与实际情况相悖的结论[5]。
而Lévy稳定分布的概率密度函数具有尖峰、拖尾、非对称的特征,与影响水工结构可靠性的随机变量的非高斯统计特征一致,因此可以通过Lévy稳定分布的稳定指数α以及倾斜指数β直接刻画出各随机变量的尖峰、拖尾和非对称特征,实现对影响工程结构可靠性随机变量统计分布的准确估计,从而得到较为准确的分析结论。整理需要研究的随机变量的数据,得到随机变量数组X=(x1,x2,x3,x4,x5)。将X视为独立同分布的随机向量,为了研究随机变量满足的统计分布,首先要确定与实际数据拟合程度最高的统计分布。本文将Lévy稳定分布、极值I型分布和对数正态分布3种统计分布作对比分析。需要指出的是Lévy稳定分布没有确定解析形式的累积分布函数和概率密度函数,目前采用的方法是首先通过Koutrouvelis和Kogon、Williams[6]提出的经验特征函数法确定各随机变量对应的Lévy稳定分布的4个参数,包括稳定指数α、倾斜指数β、尺度参数γ和位置参数δ,然后使用Nolan提出的一种直接积分法计算Lévy稳定分布的累积分布函数。
1.3 基于 Lévy稳定分布的蒙特卡罗法
本文通过Lévy稳定分布与蒙特卡罗法相结合对失效概率进行计算,具体步骤如下:
(1)确定研究对象以及随机变量并获取数据。选择合适的水工结构作为研究对象,选择影响其可靠性的因素x1,x2,x3,x4,x5…作为随机变量,并获取相关的实验数据,得到随机变量矩阵X=(x1,x2,x3,x4,…)。
(2)建立极限状态方程
g(R-S)=R-S=g(x1,x2,x3,x4,x5,…)
(4)
式中,R为容力;S为抗力;g(R,S)为X=(x1,x2,x3,x4,x5…)的函数。
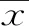
(5)
(6)
(4)计算静态失效概率。将还原后并标准化过的数据代入极限状态方程,当计算值g(X)≤a时(a为常数),水工结构将失效。对失效情况进行蒙特卡罗模拟,进行R次数值试验,则水工结构失效概率为
(7)
式中,I为逻辑指示函数;g(Xi)为失效概率计算值。当g(X)≤a时,I=1,否则,I=0。由上式可知,失效概率Pf与试验次数R有关,为保证准确性,需要计算不同试验次数R下的失效概率。
2 实例分析
2.1 Lévy稳定分布
为进一步验证Lévy稳定分布对水工建筑物影响因素的拟合优势,本文以内蒙古永济第二节制闸1995年~2001年的下游水位为例,通过K-S法来定量分析3种统计分布与实际数据之间有无显著性差异。K-S法是Kolmogorov和Smirnov提出的一种检验误差的方法,主要思想为对每一个数据进行理论观测和数值计算的比较,如果计算出的最大值偏差小于允许偏差时,认为原假设是正确的[7]。之后再绘制出不同统计分布的下游水位累积分布函数图像,可以比较出最优拟合统计分布。
图1给出了下游水位在不同统计分布下的累积分布函数。从图1可以看出,Lévy稳定分布相比于对数正态分布和极值I型分布,对实际数据的拟合程度更好。表1给出了3种统计分布的K-S检验最大误差。从表1可以看出,Lévy稳定分布的K-S检验最大误差仅为0.062 67,远小于对数正态分布和极值I型分布,由此确定,Lévy稳定分布具有最好的拟合效果。
2.2 失效概率计算
内蒙古永济第二节制闸是一座整体开放式水闸,闸室包括两扇闸门,每扇闸门都配有一座螺旋式启闭机,在河道和河道的两侧连接有钢筋混凝土的后墙。相关数据如下:闸门宽2.5 m,高3 m,自重3.25 t,中墩厚0.8 m,闸室底板顺水流方向长7.5 m。计算工况采用闸上设计水位2.6 m,闸下设计水位0.6 m[8]。在上述工况条件下,计算水闸的抗滑稳定性。《水闸设计规范》指出,水闸抗滑稳定性的主要影响因素有:水闸结构自重、上下游水压力、渗透压力、水体重力、底板与地基间摩擦力、基底粘着力及地震荷载等。在本文的计算中,选取结构自重、上游水位、下游水位、底板与地基间摩擦力、基底粘着力作为随机变量,将其依次设为x1,x2,x3,x4,x5。
以内蒙古永济第二节制闸为研究对象,采用上述失效概率预测模型分析永济第二节制闸的抗滑稳定性。建立水闸抗滑稳定性极限状态方程
g(X)=f[Wu+Wd+Ws-U]+AFg-(Pu-Pd)
(8)
式中,f为底部内摩擦系数;Wu为上游水重;Wd为下游水重;Ws为水闸自重;U为扬压力;A为底部受剪面积;Fg为基底粘着力;Pu为闸上游水压力;Pd为下游水压力。当g(X)≤0时,水闸将失效。
之后,将还原并标准化后的Lévy随机数代入极限状态方程中,进行多次蒙特卡罗模拟试验,得到失效概率Pf。本文通过Matlab软件实现对Lévy稳定分布的参数估计、概率密度函数及累积分布函数的计算、生成随机数等,并且根据蒙特卡罗法的思想编写程序计算失效概率。由大数定理可知,当试验次数R极大时,试验结果可以反映失效概率Pf。为了保证计算得到的失效概率有效,需要进行多次试验来判断收敛情况,这也使得对水闸的可靠性评估更加准确。作者通过不断增加多次试验并观察后确定失效概率Pf曲线收敛并且在一个值附近波动,当曲线趋于平稳时表明在该试验次数R下可以得到较为准确的失效概率Pf。
本文进行了10组试验次数依次递增的蒙特卡罗模拟试验,失效概率随模拟次数变化的收敛曲线见图2。从图2可以看出,当试验次数数量级达到106时,失效概率曲线开始趋于收敛,并在0.227%附近波动,相对误差不超过2%。模拟次数以及失效概率的计算结果见表2。
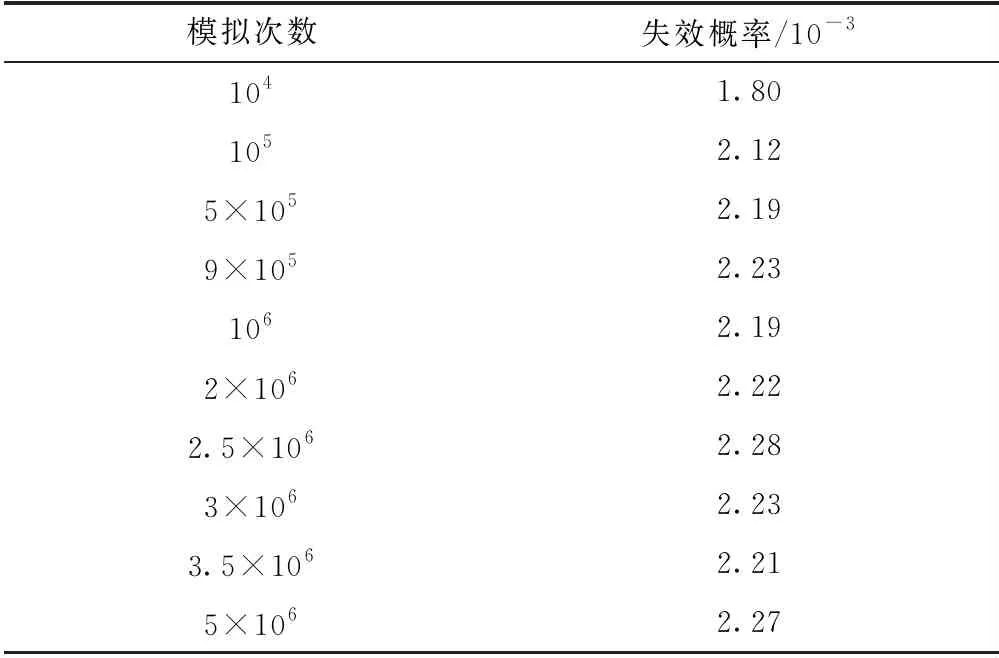
表2 模拟次数、失效概率
文献[8]给出了1995年~2001年下游水位数据,为了研究不同年份中该水闸抗滑稳定性及其变化规律,对各年数据按前述Lévy稳定分布失效概率计算方法分别进行处理。表3给出了失效概率逐年变化的计算数据。进一步观察可发现,该水闸随使用年限增加,失效概率与年份近似为线性增长关系。基于Lévy稳定分布得到的失效概率随年份变化的函数可对水工建筑物失效概率进行分析和预测。

表3 失效概率逐年变化数据
3 结 论
(1)与对数正态分布和极值I型分布相比,Lévy稳定分布作为影响水工建筑物可靠性随机变量的统计分布时对实测数据的拟合效果好,可以较好地反映水工结构水位数据的统计特征。
(2)从理论和数值计算两方面来看,基于Lévy稳定分布的失效概率预测模型是有效的,Lévy稳定分布对影响水工建筑物可靠性的各随机变量具有较好的还原性,可以据此进行失效概率的预测,分析在一定年限内水工建筑物可靠性的变化,可应用于实际工程中。

