范德瓦尔斯方程在空间充气装置设计中的应用

王 盼,叶晓滨,李旭东,吴艳红

(1.航天科工空间工程发展有限公司 空间结构技术部,北京 100080;2.凯迈(洛阳)气源有限公司 气源部,河南 洛阳 471003)

0 引言

随着航天技术的发展和各国在深空领域研究的持续深入,许多新型材料和结构正在不断地被研制并投入到航天器的设计制造中。其中,空间充气结构是一种以柔性复合材料薄膜构造的空间结构,用于制造各种类型的航天器或者航天器上的功能部件,如卫星天线、太阳能电池阵、太阳能防护罩以及空间结构的展开支撑机构等[1-2]。与传统的空间结构相比,利用充气技术构建的空间结构具有许多明显优势,例如发射体积小、结构重量轻、研究和制造成本低,并且可用于构建大型和超大型的空间结构。因此,空间充气结构技术受到了越来越多的关注,并成为空间技术领域的研究热点[3]。

对于空间充气结构而言,充气装置(介质一般为氮气)是为其提供气源的重要组成部分。按照工作气体的生成/输送方式,充气装置可以分为气瓶式充气装置、化学反应气体生成充气装置,以及这两种方式的混合充气装置。气瓶式充气装置以其高可靠性和可控性,被广泛应用于各种航天器产品中。本文将以气瓶式充气装置为背景,对范德瓦尔斯气体方程在充气装置设计中的应用进行研究。

1 气瓶式充气装置概述

气瓶式充气装置的组成一般包括高压气瓶、阀门系统(包括充气阀、自锁阀或电爆阀、减压阀、电磁阀等)、过滤器以及管路系统、压力传感器等[3]。其工作原理为:根据充气需求,向气瓶中充入适量的气体,为了留有设计裕度,充入的气量一般为所需气量的1.3～1.5倍;在航天器进入轨道,需要对充气结构进行充气时,打开阀门系统自锁阀(或电爆阀),高压气体通过减压阀、节流阀等减压、节流装置为充气结构充入气体,以达到稳压输出的目的,电磁阀作为控制充气动作开始或停止的开关元件接收航天器控制系统的指令,压力传感器可以作为充气状态反馈的元件,对充气过程以及最终充气完成状态进行反馈。简单的充气装置如图1所示。

图1 气瓶式充气装置组成图Fig.1 Composition diagram of the gas cylinder inflatable device

气瓶式充气装置设计的一般思路为:首先,根据充气需求,如空间充气结构所在环境温度、所需充气体积、充气压力等,以及航天器机械总体的布局要求,进行充气装置各元器件的初步设计,如气瓶内部的储气压力、减压阀的减压比、自锁阀以及电磁阀的承压能力、压力传感器的量程及精度等;然后,根据研制任务对充气装置的环境要求,如力学环境要求、热环境要求、空间环境要求等,对各元器件进行选型或设计;最后,根据机械总体的布局要求进行各元器件具体的布局设计和管路系统设计。

表1 充气要求Tab.1 Requirements for air inflation operation

2 范德瓦尔斯方程在充气装置设计中的应用

2.1 范德瓦尔斯方程简述

在充气装置设计过程中,气体物态方程是必要的应用条件。pV=nRT是理想气体方程,理想气体反映实际气体压力趋于0时的极限性质,理想气体忽略了气体分子的体积和分子间相互作用力。在常温常压下,也可以把实际气体近似地当做理想气体[4]。

然而,在高压和低温环境条件下,实际气体与理想气体的偏离较大,充气装置在轨道空间环境下一般都包含高压(气瓶自身高压贮气特点)或者低温的环境特性,使用理想气体方程用于空间产品过程设计会导致精度降低[5]。为了更加真实地描述实际气体的行为,荷兰物理学家范德瓦尔斯引入了气体体积修正参数和分子引力修正参数,得到了著名的范德瓦尔斯物态方程(推导过程参见文献[4])

(1)

式(1)为1 mol气体的范德瓦尔斯方程，1 mol气体的修正量a和b称为范德瓦尔斯常量，对于充气装置设计而言，a的单位可取“MPa(mL/mol)2”，b的单位可取“mL/mol”，对于特定的气体，范德瓦尔斯常量都有确定的值，对于不同种类的气体，范德瓦尔斯常量也不同；Vm为1 mol气体所占据的体积；R为气体常数，取值8.314 J/(mol·K)；T为绝对温度，单位K。

质量为m体积为V的气体的范德瓦尔斯方程一般形式为：

(2)

式中:M为气体的摩尔质量，修正量a和b与1 mol气体的修正量a和b相同。如果将气体的密度ρ引入，可得到范德瓦尔斯方程的另一变种形式：

(3)

根据热力学第一、第二定律对范德瓦尔斯气体的讨论,发现范德瓦尔斯气体状态方程相对于理想气体方程,在描述真实气体的性质方面更具优势[6]。

2.2 范德瓦尔斯方程的应用

高压气瓶做为充气装置的关键组成部件,对其设计的精确度和可靠度是保证充气装置整体质量水平的重要设计环节。以某型航天器的充气结构充气要求(如下表1)为例,对范德瓦尔斯方程在充气装置设计过程中的应用做如下阐述,其中涉及的压力如果不做特殊说明,均为绝压。

根据充气要求，初选气瓶工作压力P=15 MPa，容积为V(需要计算的物理量)。

根据充气装置管路出口压力应满足(800±100) kPa的要求可知，当气瓶内部剩余气体压力低于(800±100) kPa时，充气装置就不能继续给展开结构充入气体，计算时，取气瓶内部余气压力P1=0.9 MPa；充气结构展开后内部压力为0.05 MPa。

低温时，气体压力变小，以-50 ℃为计算输入，计算压力为0.9 MPa(余气)以及0.05 MPa(需充气)下气体(N2)的密度。地面给气瓶充气的过程取常温20 ℃。

为了得到气瓶的容积V，需要计算得出不同状态下氮气的密度。由式(3)可知，范德瓦尔斯方式是关于密度ρ的三次方程，手算过程较为繁琐，可借助matlab计算工具进行数值计算，以0.9 MPa、-50 ℃为例，计算过程如下：

第1步：声明变量，T，M，p为绝对温度、摩尔质量、压强；ρ为密度；a，b为范德瓦尔斯常量。

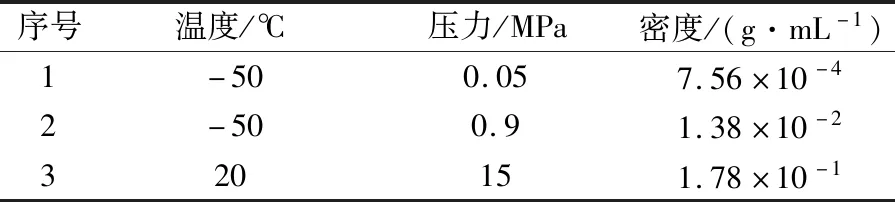
表2 3种状态下氮气密度Tab.2 Nitrogen densitiesunder three conditions

matlab语句为：symsTMpρab

第2步：为各个变量赋值。

matlab语句为：T=(-50+273.15);M=28;p=0.9;a=1.39×105;b=39;

第3步：建立范德瓦尔斯方程。

matlab语句为：eqn=8.31*T/(M*(1/ρ-b/M))-(a*ρ^2)/M^2=p;

第4步：三次方程求解

matlab语句为：ρ=solve(eqn);

用此方法解出的3种状态下氮气的密度如表2所示

由此可得充气展开结构需要的充气量m1=7.56×10-4×50 000=37.8 g ；

气瓶内余气量m2=1.38×10-2×V；

气瓶在地面充气时，总的充气量m=1.78×10-1×V；

根据质量守恒，m=m1+m2，计算得出气瓶容积V≈230 mL 。

由以上计算得到气瓶的容积，再结合气瓶设计的行业规范，确定其安全系数，考虑机械总体的布局约束，便可得到气瓶具体的形状尺寸，从而对充气装置进行详细的工程设计。

如果初步设计中预先给定了气瓶的容积，根据范德瓦尔斯方程，同样可以得到该容积下气瓶的工作压力等参数，形成闭环设计。

3 与理想气态方程的对比

为了直观地对两种气态方程的差异进行进行对比，选取不同的工况，对氮气(N2)的密度进行统计计算。

质量为m的理想气体方程为：

(4)

式中：M为气体的摩尔质量；m为气体质量；R为气体常数；T为绝对温度。

将密度公式带入式(4)，可得到带有密度参数的理想气体方程

(5)

对比工况一：

气体压力为10 MPa，温度分别为0 ℃，-20 ℃，-40 ℃，-60 ℃，-80 ℃，计算出的密度均以g/mL为单位，计算结果如表3所示。

表3 压力为10 MPa,不同温度下的密度Tab.3 Densities at different temperatures under 10 MPa

对比工况二:

气体温度为-20 ℃,压力分别为10 MPa,20 MPa,30 MPa,40 MPa,50 MPa,计算出的密度均以g/mL为单位,计算结果如表4所示。

表4 温度为-20 ℃,不同压力下的密度Tab.4 Densities under different pressures at fixed temperature of -20 ℃

如上所述,一般情况下,温度越低、压力越大,则范德瓦尔斯气体方程与理想气体方程的计算结果差异就越大,而且达到一定工况条件后,这种差异是不可忽略的。

4 总结

以范德瓦尔斯方程在空间充气装置设计中的应用为研究目标,首先,对充气结构技术在航天器上的应用进行了概述,并对气瓶式充气装置进行了必要的介绍,包括其一般组成、工作原理和设计思路;然后,结合某充气要求的具体工况(包括充气体积、充气压力、工作温度等)对范德瓦尔斯方程的应用过程进行详细描述,求得该充气装置气瓶的容积。为进一步反映范德瓦尔斯方程在设计过程应用的必要性,将范德瓦尔斯方程与理想气体方程在不同工况下的计算结果进行了对比,揭示出了低温、高压下范德瓦尔斯气体方程与理想气体方程计算结果的差异性。

另外,有学者对遵从推广的范德瓦斯方程进行研究,将温度变化对气体实际行为的影响做了深入详细地描述,并得出有益结论。还有部分学者通过试验,对适用于精细研究和应用的气体热力学RK方程进行了研究,得出了温度变化对RK系数的实际影响[6-8]。但对范德瓦尔斯方程本身来讲,其特点是方程形式简单、物理意义明确,而且,对于工程应用而言,在设计中一般都会留有适当的设计裕度,所以,在空间充气装置的设计过程中,范德瓦尔斯方程的应用将会起到重要的作用。