层流机翼飞行验证平台雷诺数效应分析及修正

杨钊，李杰，牛笑天

西北工业大学 航空学院，西安 710072

当前，在气动力相关性分析研究中一个主流趋势是将CFD、风洞试验和飞行试验这3种用于确定飞机气动特性的技术手段紧密结合起来为飞行器的设计提供有力的支撑。图1显示了3种方法各自的特点和它们之间的区别。CFD和风洞试验一般用于在设计研制阶段初步确定飞行器的基本气动特性，而飞行试验则通常用来在最后阶段对飞行器真实飞行性能进行综合评估。通过建立3种分析手段之间的关联模型，便可以利用CFD手段辅助数据修正，发展从地面风洞试验数据向天上真实飞行数据的外推方法，从而尽可能在飞行试验开展之前完善飞行器的总体设计[1]，同时也能够为飞行试验计划提供参考。对于CFD计算分析而言，可以针对全尺寸飞机几何外形开展数值模拟研究，状态可以涵盖完整的飞行工况，并且不存在雷诺数效应问题，能够作为缩比风洞试验和飞行试验之间的桥梁，在风洞试验数据的修正和飞行结果的对比校验中都发挥着相当重要的作用[2]。

图1 确定飞机气动特性的技术手段和方法

相关性分析中最重要的一个方面就是对飞行器雷诺数效应的分析和修正。对于一般的附着流动来说，雷诺数的大小影响模型表面上附面层的性质，从而改变附面层的厚度、附面层转捩位置、表面摩擦阻力以及与气体黏性有关的气流分离情况。这样，在试验雷诺数与飞行雷诺数相差较大的情况下必然导致风洞试验数据与飞行情况不一致[3-4]。换言之，两种雷诺数之间的差异使风洞试验数据的准确度受到了影响。雷诺数效应又可分为直接雷诺数效应和间接雷诺数效应[1]。直接雷诺数效应是与恒定压力分布有关的效应，而间接雷诺数效应则与雷诺数变化时压力分布的变化有关。通常依赖于间接雷诺数效应的气动特性是：升力和俯仰力矩、波阻、阻力发散和抖振边界；而依赖于直接雷诺数效应的特性主要有：黏性阻力、边界层分离特性和抖振边界。众所周知，边界层的流动转捩位置也会随雷诺数变化而发生改变。由于层流边界层更容易分离，而湍流边界层在一定雷诺数下具有更高的壁面摩阻，因此飞机的阻力和升力都会随着转捩位置的改变而发生不同程度的变化。因此，雷诺数的变化不仅会直接影响到全机的主要气动力特性，还能够通过改变表面流动转捩位置来间接对升、阻力及力矩特性等产生影响[1]。

在风洞试验中，模型尺寸远小于真实飞机，因此试验雷诺数远小于飞行雷诺数。这种由雷诺数差异所引起的“雷诺数效应”对附面层的结构和飞机的气动特性往往有着不可忽略的影响。一般来说，低雷诺数风洞试验结果主要会存在以下问题[4]：

1) 大迎角时气流分离比真实飞行提前，影响飞机的最大升力系数以及其他与分离有关的气动特性。

2) 飞机表面摩擦系数与真实飞行相比偏大，雷诺数的差异会显著影响飞机的阻力系数(最小阻力系数、零升阻力系数、升致阻力因子等均是雷诺数的敏感项)。

3) 风洞试验中飞机表面附面层状态与真实情况下有很大不同，从而使表面各种小的突出物对全机阻力的影响也不同。

4) 雷诺数会对物面边界层的流动转捩特性产生显著影响，进而影响到全机的升阻特性和压力分布特征。通常来说，风洞试验中所得到的层流流动转捩位置与真实情况相比会有所推迟。

近年来，国内外利用高雷诺数或变雷诺数试验[5-10]针对各种类型的飞机开展了大量的关于雷诺数效应的试验研究，取得了丰硕的成果。但是大量的风洞试验所带来的高昂费用是设计人员们不得不面临的一个严峻的问题。因此，通过数值模拟方法来研究飞行器的雷诺数效应逐渐成为研究热点。Pettersson等开展了运输机构型雷诺数影响的数值研究[11]；Said等通过数值模拟方法研究了雷诺数对三角翼流场和气动特性的具体影响[12]；Rudnik等利用CFD方法研究了雷诺数的差异对某增升构型低速气动特性的影响规律[13]；Curtin等则深入探究了跨声速飞行状态下雷诺数效应对双发运输机构型气动性能的影响[14]。近年来，国内同样在这方面开展了很多的研究工作。周林[15]、马明生[16]等通过数值计算研究了雷诺数效应对于运输机构型气动性能的具体影响规律；张培红等[17]采用CFD方法，同时结合风洞试验数据开展了雷诺数对某飞机气动性能的影响研究；张彦军等[18]采用试验和数值计算两种手段分别研究了雷诺数差异对于超临界翼型气动性能的影响；李中武等[19]开展了低速增升装置变雷诺数的计算研究。通过这些研究进一步加深了研究人员对于雷诺数效应的认识，也更加清晰地得到了雷诺数对于飞机气动性能的具体影响规律。

图2中的阶段1部分给出了本文的主要研究路线和内容，同时也表明本文研究工作在整个层流机翼设计、验证和评估项目中的重要性。文中利用数值计算方法针对特殊布局形式的层流机翼飞行验证平台低速起降和高速巡航构型在试验和飞行雷诺数下进行数值模拟分析，以得到全机气动力系数和流场结果。通过计算结果与风洞试验数据的对比分析，进行已有数据的相互校验。同时，深入剖析雷诺数效应对飞行验证平台高、低速气动性能、低速失速分离特性和高速层流转捩特性等的具体影响规律，并据此对低速和高速试验数据进行修正，为后期阶段2中飞行试验的设计提供数据支撑，协助完成国内首次基于高亚声速无人验证平台开展的高空层流流动验证工作，实现阶段3中层流机翼设计效果的综合评估。

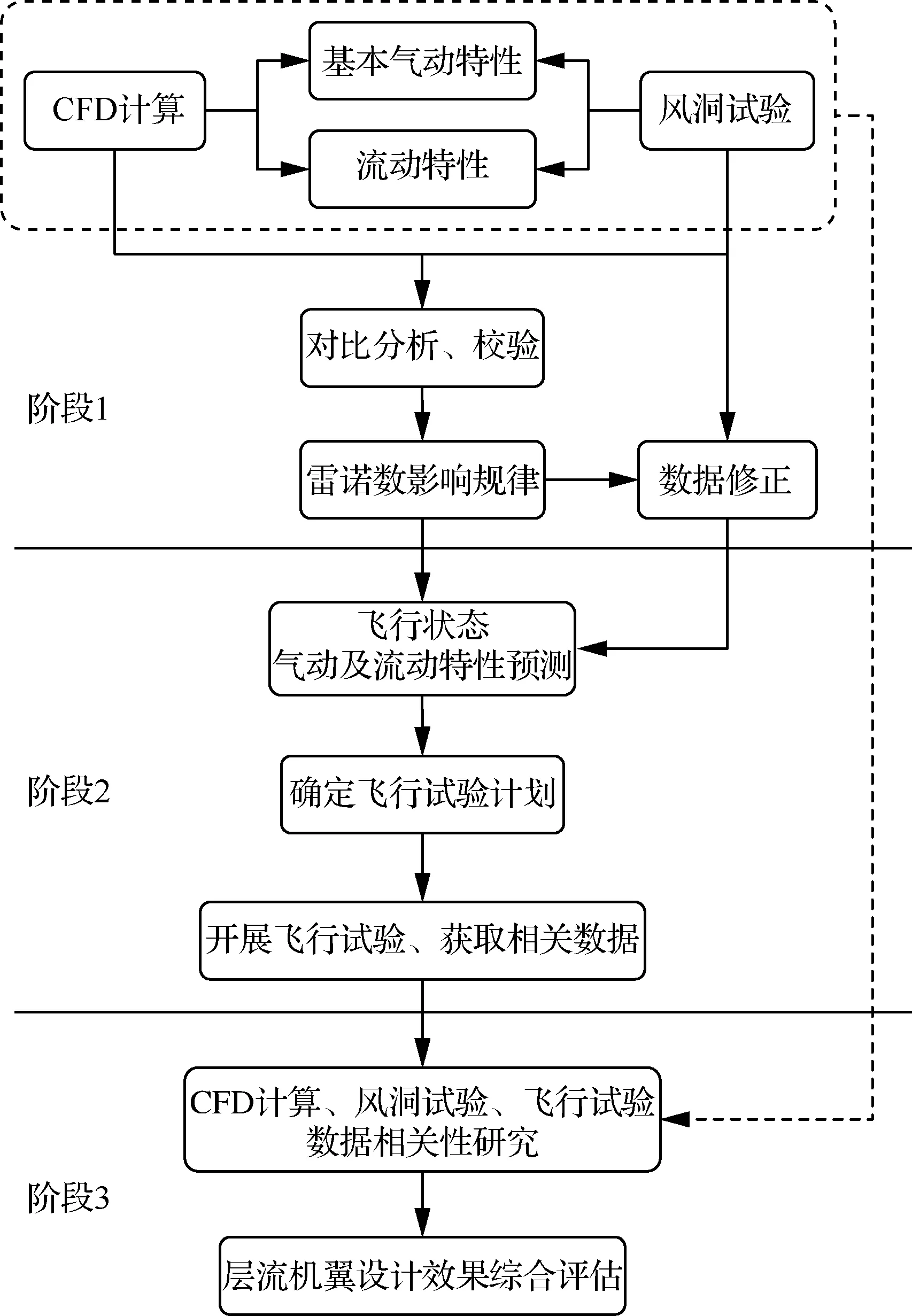
图2 研究路线图

1 风洞试验

本文的研究对象是航空工业第一飞机设计研究院研制的层流机翼飞行验证平台，是国内首个为开展层流飞行试验设计的高亚声速无人飞行平台。该平台气动布局采用双机身、π型尾翼设计，外翼下吊装4台小型涡喷发动机。机翼分为内、外翼两段，内翼段为层流验证段，上表面光滑，且无运动翼面。外翼段后缘内侧为单缝简单偏转式襟翼，供起飞、着陆时增升使用，外侧为副翼控制面。尾翼为π字型结构，双垂尾底部分别和双机身尾部相连，顶部则与平尾相连。垂尾和平尾后缘分别设有方向舵和升降舵。该特殊布局层流机翼飞行验证平台的主要几何参数如表1中所示。

表1 飞行验证平台几何参数

针对该层流机翼验证平台的低速风洞试验是在航空工业空气动力研究院的FL-8低速风洞中进行的，风洞试验中采用的是1∶3.25的缩比模型，试验雷诺数大概在150万量级。风洞试验模型示意图如图3所示。该低速试验采用腹撑式天平进行测力，并通过图 4所示的对称天平测量试验来定量扣除天平装置气动外形对飞机流场和气动力的影响。

图3 低速风洞试验模型示意图

图4 天平影响测量试验

高速风洞试验是在航空工业空气动力研究院的FL-2风洞中进行的，风洞试验中采用的是1∶7的全金属通气缩比模型，试验雷诺数大概在300万量级。风洞试验模型示意图如图5所示。全模测力主支撑形式为中央翼段下部畸变的尾支撑形式，畸变带来的支撑干扰通过双支杆支撑方式进行扣除。试验模型在风洞试验中的具体支撑形式如图6所示。

图5 高速风洞试验模型示意图

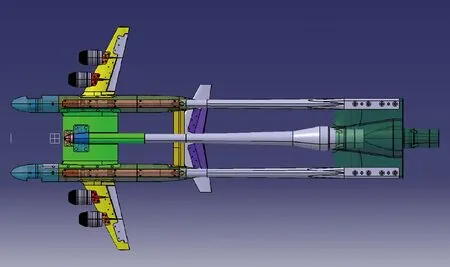
图6 试验模型在风洞中的支撑示意图

2 计算方法

数值模拟计算主要采用NASA的CFL3D求解器。其作为一种多块结构网格求解器，计算效率高，计算精度基本满足工程应用要求，适合作为飞机设计研制过程中的计算分析和设计辅助手段。

2.1 控制方程

CFL3D求解器采用积分形式的雷诺平均Navier-Stokes方程作为流场控制方程：

(1)

式中：V为控制体体积；S为控制体表面积；Q为守恒变量向量；f为通过控制体表面的通量向量，包含3个方向的无黏和黏性通量；n为控制体表面的外法向单位向量。

采用格心格式的有限体积法对控制方程进行离散，其中黏性项的空间离散采用二阶中心差分格式，无黏项则采用二阶Roe迎风通量差分格式离散。时间项采用双时间隐式近似因子分解法(A-F)进行推进，计算中应用了多重网格技术加速流场收敛。

2.2 转捩模型

(2)

γ间歇因子输运方程的作用是进行转捩的判定和对转捩区的发展进行预测，具体形式如下：

(3)

为了模拟分离诱导转捩，对输运方程做了特殊处理，使得γ在流动分离处快速增长，以模拟层流分离/湍流再附现象，主要的修正如下：

(4)

(5)

γeff=max(γ,γsep)

(6)

上公式中涉及到相关变量的具体定义详见文献[20-22]。

2.3 计算模型与网格

CFD计算采用如图7中所示的真实尺寸全机模型，模型中设置有襟翼、副翼、升降舵和方向舵等部件，舵面与其他部件之间留有缝隙。计算网格采用多块结构化网格划分，计算区域的远场边界流向前后取30倍平均气动弦长，展向和竖直方向各取为20倍。附面层第1层网格高度为5.0×10-6m，法向增长率为1.15，物面网格的y+值均小于1[23]。y+是与壁面第1层网格间距和具体流动参数直接相关的无量纲壁面距离，表征的是第1层网格点在附面层分区结构中的位置。对于中央翼段进行流向加密，以满足高速状态层流计算的要求，最终总网格量为3 000万左右，计算中所采用的验证平台表面网格如图8所示。

图7 计算模型三视图

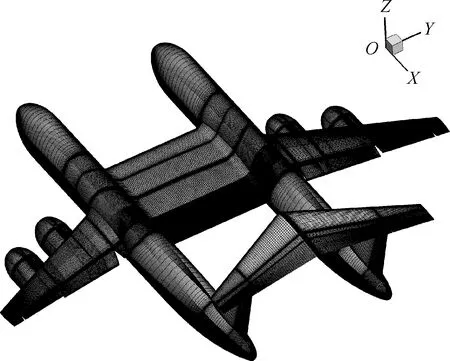
图8 计算网格

3 计算结果与讨论

3.1 CFD计算状态

针对层流机翼验证机低速起降构型(襟翼下偏30°)和高速干净构型(襟翼下偏0°)不同马赫数飞行状态,分别开展试验和飞行雷诺数下的数值计算分析，所有的CFD计算状态如表2所示。通过气动力系数计算结果与试验数据的对比验证了方法的计算能力和可靠性。同时利用不同雷诺数下的计算结果分析总结雷诺数的差异在低速和高速状态下对全机气动性能的影响程度和具体规律。

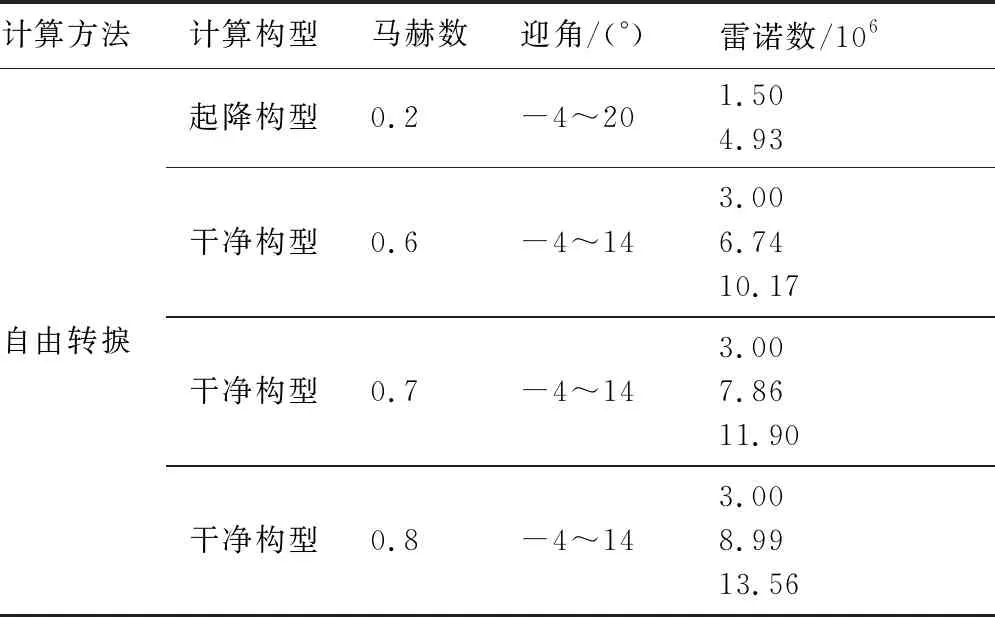
表2 CFD计算状态

3.2 低速飞行状态雷诺数影响

针对低速起降构型飞行雷诺数和试验雷诺数下的数值计算结果(Cal)与试验数据(Exp)的对比如图9所示。可以看出，-4°～8°迎角之间计算所得升力系数CL与试验数据吻合较好；计算与试验零升力矩相差不大，但试验结果中的纵向稳定度略大于数值预测结果。低速状态下雷诺数的差异对线性段小迎角状态的升力和力矩系数Cm影响不大，主要会对失速迎角附近的全机升力特性产生较为明显的影响。高雷诺数状态全机升力线性段由低雷诺数状态下的8°迎角增加至10°以上，最大升力系数也由低雷诺数时的1.28增加至1.35左右。可见，在低速时雷诺数的增加会明显提升大迎角状态下机翼表面流动的稳定性，进而改善层流机翼飞行验证平台的失速特性。

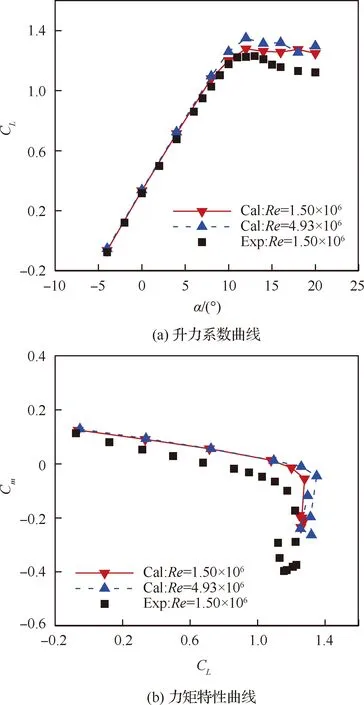
图9 Ma=0.2不同雷诺数下的全机气动力系数结果

图10给出了Ma=0.2，不同迎角下两种雷诺数状态计算所得全机表面压力分布云图和流线的对比。从图中可以明显看出雷诺数对于大迎角翼面流动状态的具体影响规律:在8°～12°迎角范围内高、低雷诺数状态下中央翼段上表面流动状态总体差异不大，而外翼段表面的流线形态差别则非常明显。低雷诺数状态外翼段外侧在8°迎角时即存在显著流动分离现象，并随着迎角的增大分离区域进一步扩大；而高雷诺数状态下直到12°迎角时翼面上大部分区域依旧保持着较好的附着流动，只在翼根部分出现了局部的流动分离现象。这充分表明雷诺数的增加能够显著提升大迎角状态机翼表面流动的稳定性。

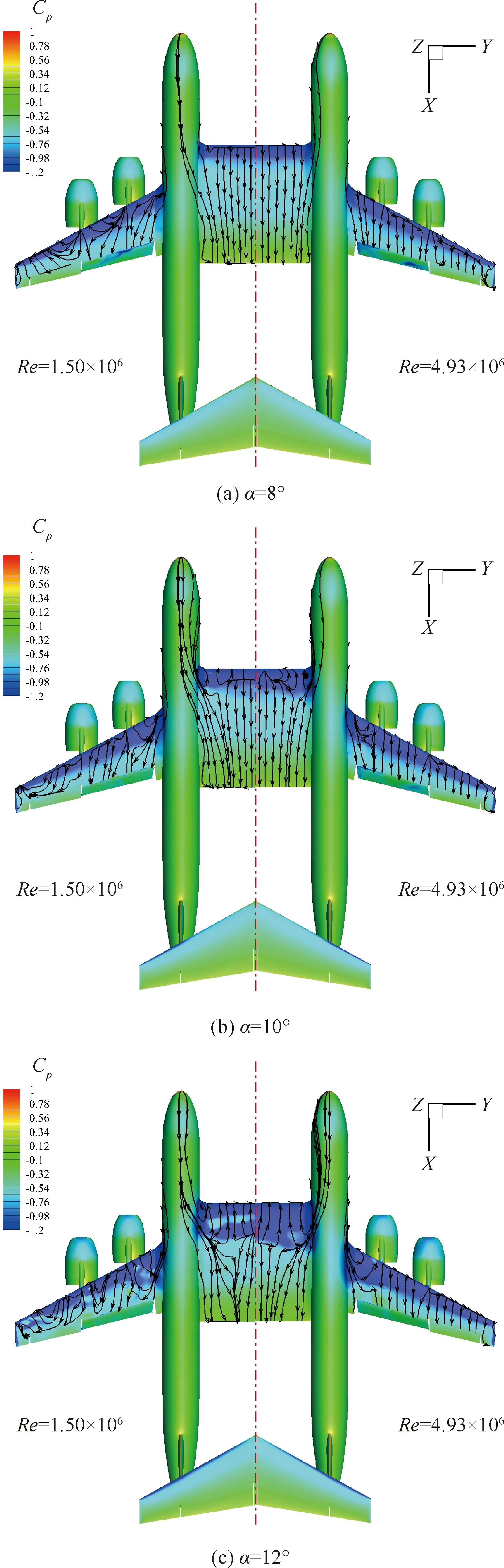
图10 Ma=0.2不同迎角下的表面压力分布云图及流线

风洞试验雷诺数计算状态，8°迎角下机翼表面出现局部流动分离，升力系数进入非线性区域，针对8°迎角下的表面压力分布和流线结果开展进一步分析。图11给出了机翼展向压力分布截面所对应的站位信息。图 12则显示了8°迎角下自由转捩计算所得不同雷诺数下机翼展向不同站位截面压力分布曲线的对比。可以看出，试验雷诺数下中央翼段和外翼上表面前部均存在明显的锯齿状，表明在此处预测到前缘层流分离泡现象；而对于飞行雷诺数计算结果，其前缘压力分布曲线相对较为光滑，未能从中观察到明显的层流分离泡现象。图13两种雷诺数下中央翼段前缘表面压力分布云图及流线可以更为直观的看出不同计算结果的差异。试验雷诺数下前缘分离泡的尺寸和分离程度要明显大于飞行雷诺数下的计算结果。

图11 机翼展向压力分布截面站位示意图

图12 α=8°机翼展向不同站位压力分布曲线对比

图13 Ma=0.2不同雷诺数下的中央翼段前缘表面压力分布云图及流线

图13中所表现出的现象与图14中央翼段前缘附近表面摩擦力系数云图的结果相一致，试验雷诺数下上表面前缘附近存在明显的分离区。从图15中展向15%站位和65%站位表面摩擦力系数分布曲线的对比中能够更加直观的看出两种雷诺数下机翼前缘流动分离特性的差异。在试验雷诺数下两个站位处均有明显的层流分离泡存在，尤其是在外翼段，其前缘分离区域长度将近局部弦长的25%；而对于飞行雷诺数，15%站位处前缘分离极小，而在65%站位处表面分离区长度也不及局部弦长的10%。

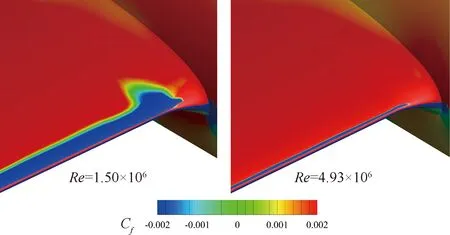
图14 Ma=0.2不同雷诺数下的中央翼段前缘表面摩擦力系数分布云图

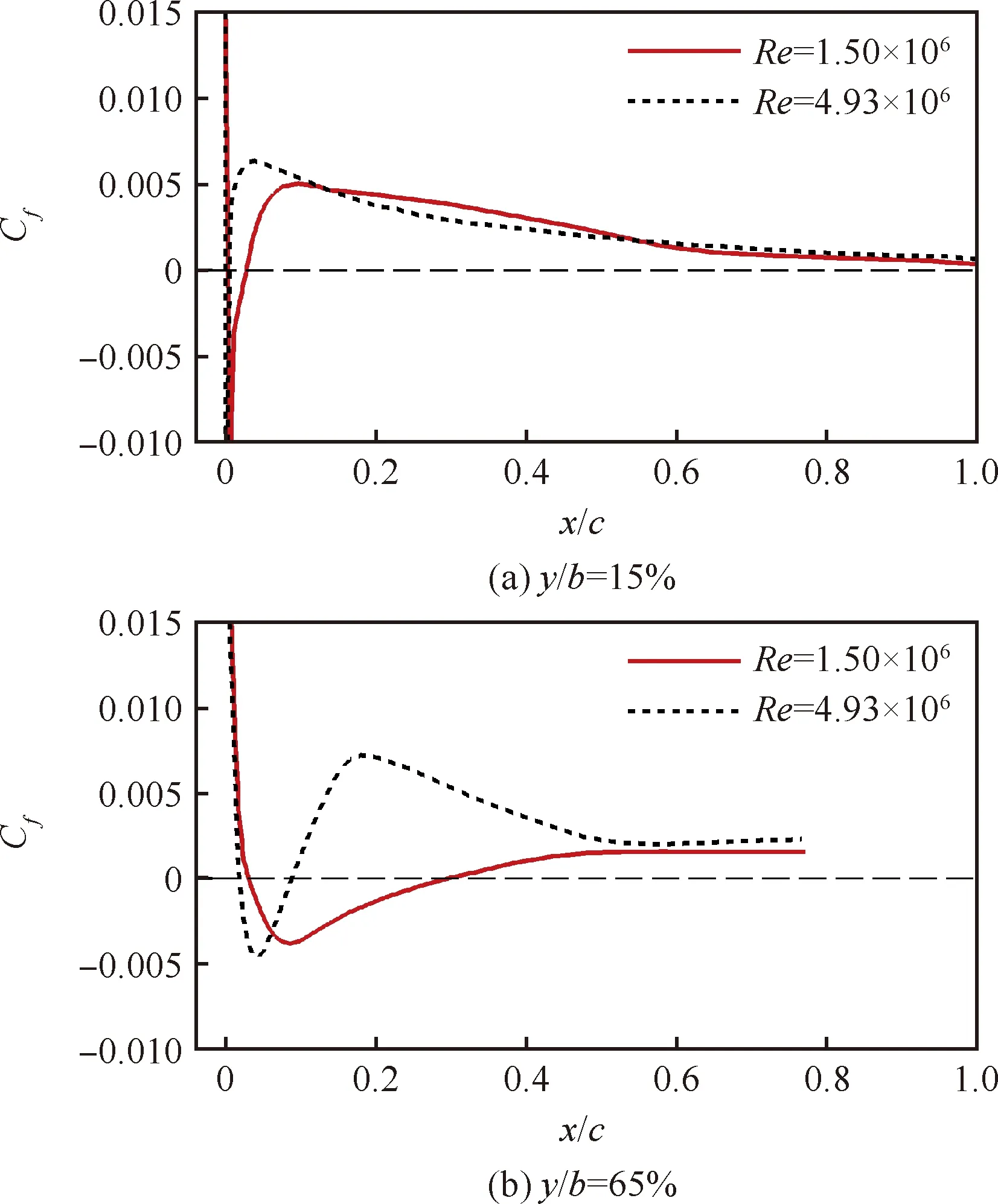
图15 α=8°机翼展向不同站位表面摩擦力系数分布曲线对比

3.3 高速飞行状态雷诺数影响

针对干净构型高速不同马赫数状态的计算气动力系数与试验结果的对比如图16中所示。可以看出，雷诺数对不同马赫数下的全机升力系数影响相对较小。从300～1 000万雷诺数以上线性段升力系数均与试验数据吻合良好。雷诺数的差异对于全机的阻力和纵向力矩系数影响较为明显。由于采用自由转捩方式进行计算，雷诺数对阻力的影响规律与全湍流计算状态下有所不同，试验雷诺数300万状态下小迎角阻力系数最小，中等和高雷诺数状态阻力系数差异不大，均略高于低雷诺数状态。这主要是因为雷诺数增加会导致翼面流动转捩特性发生变化，进而改变全机表面摩擦阻力量值。由于验证机在试验和计算中所采用短舱模型略有差异，试验和计算所得阻力量值整体差距偏大，但是数值计算结果中依旧能够反映出雷诺数对整体阻力特性的影响规律。从全机纵向力矩特性曲线来看，不同马赫数状态试验雷诺数下的计算结果在绝对量值和纵向稳定度方面均与试验数据吻合得更好。对于马赫数0.6和0.8状态试验雷诺数下的力矩结果与中、高雷诺数差异较大；而马赫数0.7下3种雷诺数的计算结果之间则差异相对较小。

图16 不同马赫数状态全机气动力系数曲线

高速飞行状态下雷诺数的差异不仅会影响全机基本气动力系数，还会对全机表面，尤其是中央层流验证段上表面的层流转捩特性产生明显的影响。风洞试验中来流湍流度大致为0.3%～0.4% 之间，计算采用的自由来流湍流度为0.3%，黏性比为10，计算中维持流动湍流度沿流向不发生明显衰减。图17中展示了Ma=0.7、迎角为2°时不同雷诺数下的全机表面摩擦阻力系数云图。可以看出，随着雷诺数的增加层流转捩位置呈现出逐渐提前的趋势，当雷诺数达到11.90×106时中央翼段上表面仅剩22%倍弦长的层流区长度。图18给出了不同雷诺数下预测所得中央验证段上表面转捩位置与试验结果的对比。在试验雷诺数的范围内试验结果与数值预测结果有一定的差异，但整体绝对量值差异不大，并且计算中所得转捩位置随雷诺数的变化趋势与试验结果基本一致。

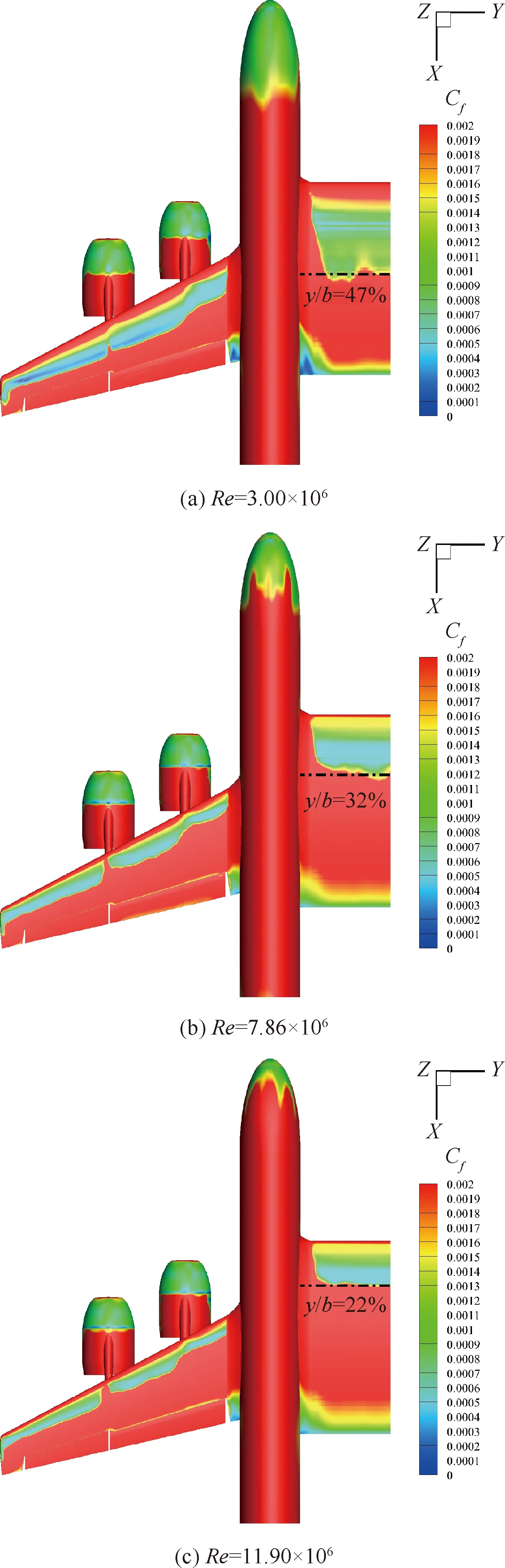
图17 Ma=0.7、α=2°时不同雷诺数下的全机表面摩擦阻力系数云图

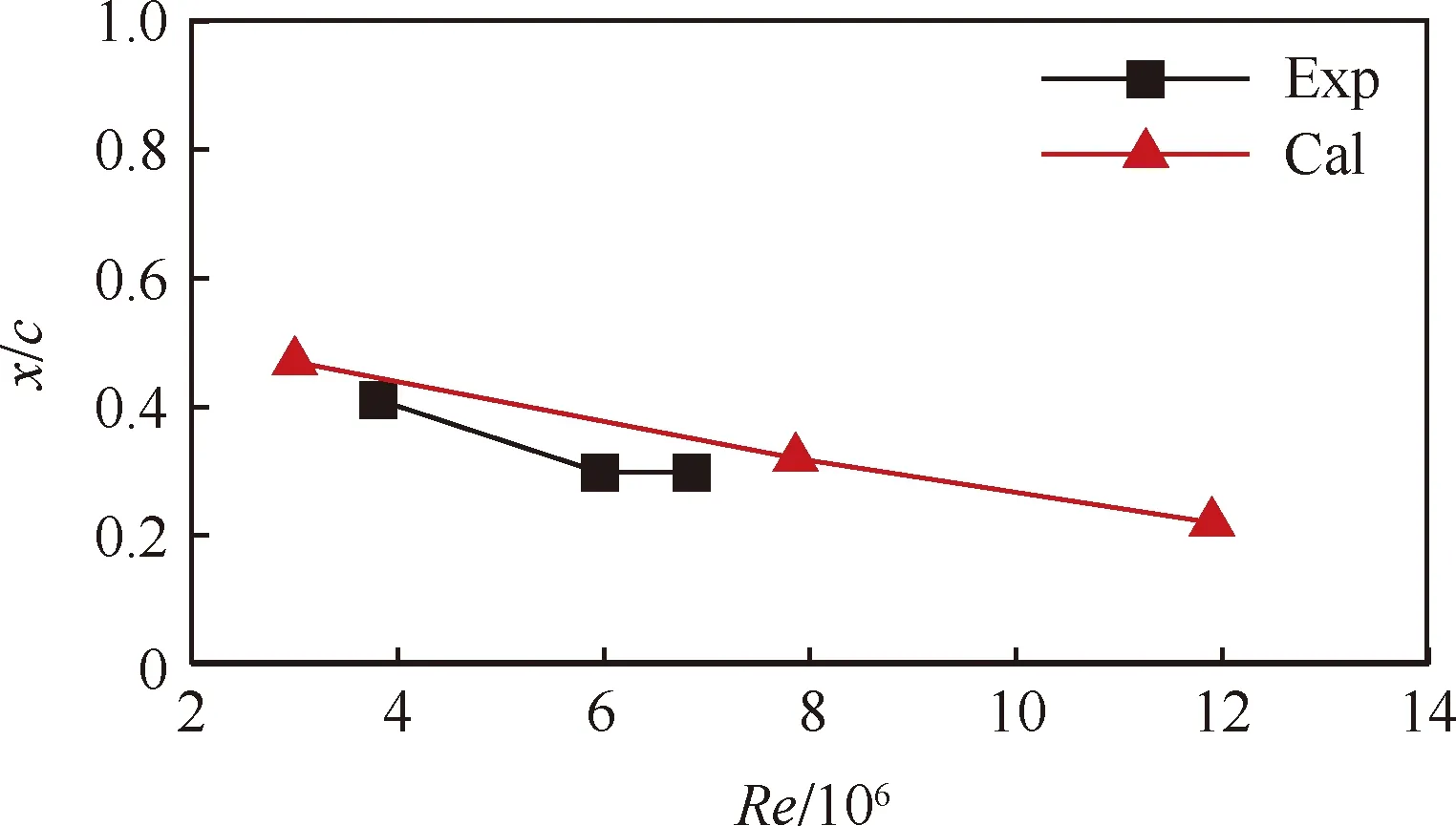
图18 Ma=0.7、α=2°时预测所得中央翼段上表面转捩位置与试验结果的对比

图19展示了马赫数0.7、迎角2°状态不同雷诺数下中央翼段上表面监测点处湍动能沿法向的分布。监测点设置在对称面上，沿流向距离机翼前缘0.2倍弦长处。横坐标k代表湍动能的绝对量值，纵坐标代表沿着壁面法向的各个点与壁面的绝对距离h。可以看出，在该监测点处随着流动雷诺数的增大边界层的厚度逐渐变薄，但其内部湍动能的峰值却会明显增加。因此，雷诺数的增加会使得边界层内部流动动能和不稳定性均大幅提升，导致流动转捩更容易发生。

图19 Ma=0.7、α=2°时不同雷诺数下预测所得中央翼段上表面转捩位置与试验结果的对比

图20给出了全机表面压力分布截面站位示意，在内、外翼段及平尾上各取多个展向截面，并对所得不同雷诺数下的压力分布曲线进行对比，分别如图21和图22中所示。由图可以看出，在2°迎角状态3个不同雷诺数下，内、外翼段表面各个站位截面压力分布曲线差异相对较小，主要集中在上表面前部和中部区域；并且，雷诺数的差异对于机翼外段压力分布的影响更为明显一些。雷诺数的改变对平尾截面压力分布形态也有一定程度的影响，但从压力分布结果的对比中未观察到显著的规律性。而雷诺数的差异对平尾截面压力分布形态的影响则稍大一些。

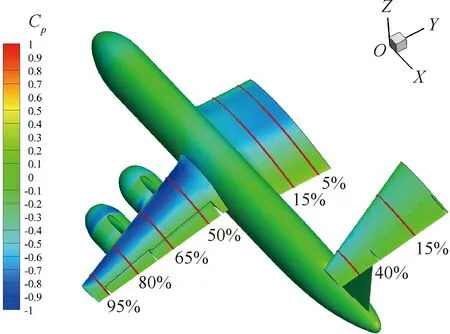
图20 压力分布截面位置示意

图21 Ma=0.7、α=2°时不同雷诺数下的内外翼段展向不同站位截面压力分布曲线对比

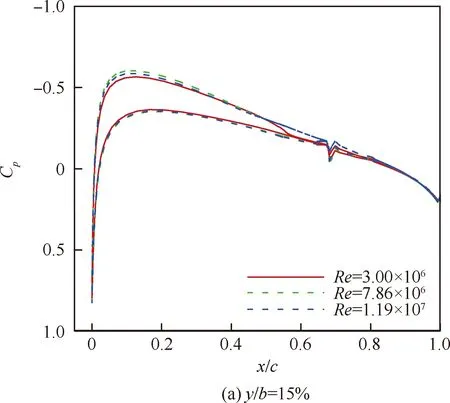
图22 Ma=0.7、α=2°时不同雷诺数下平尾展向不同站位截面压力分布曲线对比

3.4 高低速飞行状态雷诺数效应修正

鉴于文中变雷诺数CFD计算结果所体现出的雷诺数影响规律基本符合相关物理机理，气动力及流动状态差异可以得到合理解释，同时计算结果与高低速状态风洞试验结果之间也具备很好的数据相关性，采用如图23所示的雷诺数效应修正思路，将CFD计算中获取的雷诺数差异引起的气动力系数差量叠加在对应的基础风洞试验数据上，从而获得真实飞行状态气动力数据预测值。对于高速状态试验迎角范围比计算迎角范围小的问题，首先利用试验迎角范围之外试验雷诺数下的CFD计算结果，以试验迎角区间边界点上的各个气动力系数的吹风结果为基准，进行数据平移以将风洞试验结果向外拓展；而后，在此基础上通过差量叠加的方式进行雷诺数效应的修正。图24 和图25分别给出了低速马赫数0.2和高速马赫数0.7状态下风洞试验数据修正实例。真实飞行状态气动力数据预测值反映出了本文通过数值计算所得到的雷诺数对验证平台低速和高速气动力系数的基本影响规律，具备一定的合理性。

图23 雷诺数效应修正思路

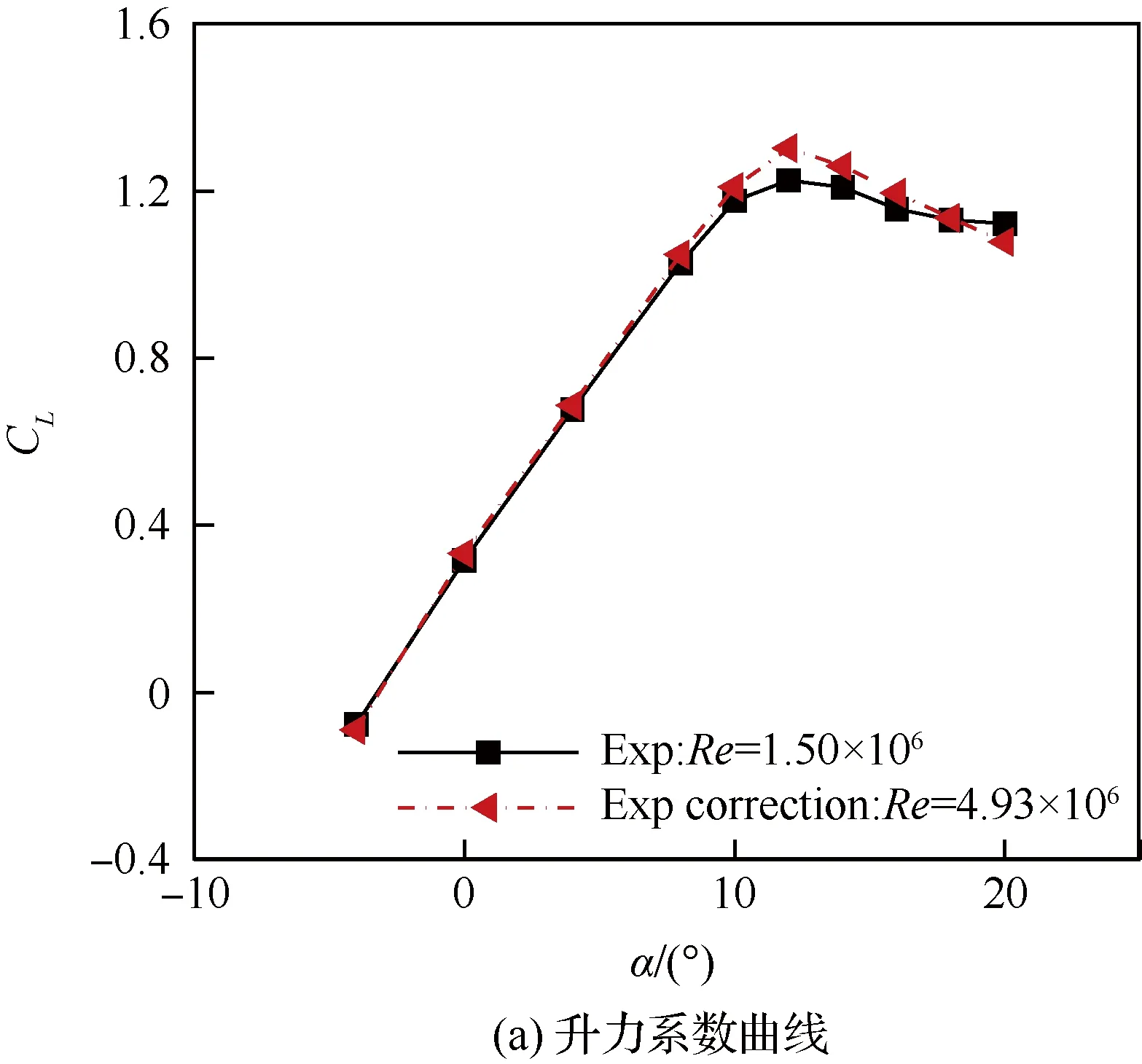
图24 Ma=0.2基于自由转捩CFD计算结果的风洞试验气动力系数修正

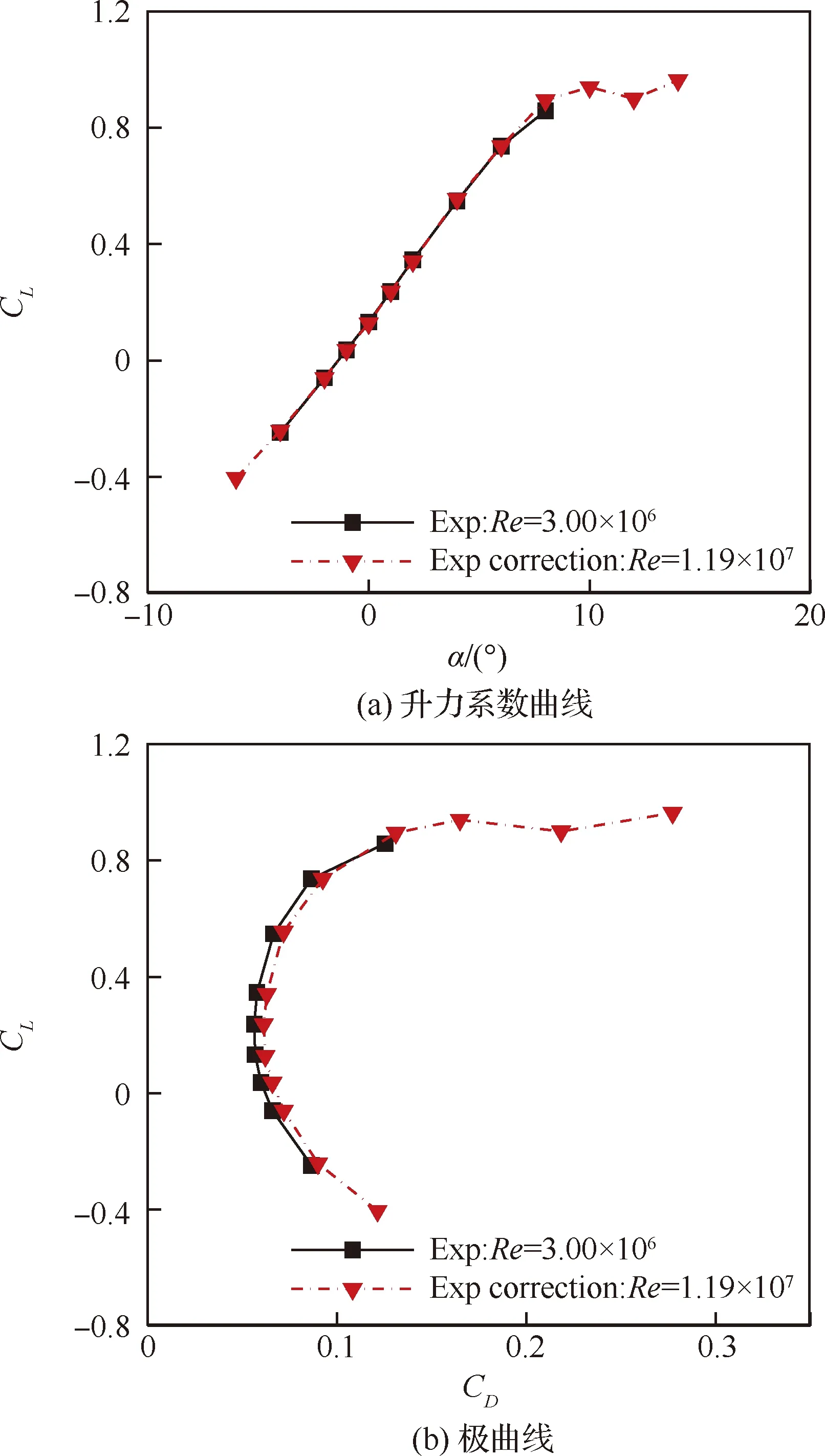
图25 Ma=0.7风洞试验气动力系数雷诺数修正

4 结 论

采用基于当地流动变量的转捩预测方法，针对层流机翼飞行验证平台低速起降和高速巡航构型分别在试验和飞行雷诺数下进行数值模拟分析。通过计算结果与风洞试验数据的对比分析，验证了结果的可靠性和准确性，归纳总结了雷诺数效应对验证平台高低速全机气动特性、低速大迎角流动分离状态以及高速层流转捩特性的具体影响规律和机理如下：

1) 低速飞行状态，试验和飞行雷诺数下计算所得升力系数在线性段范围内均与试验值吻合良好，在非线性段则较试验值整体偏高，且变化形态更加和缓；试验所得最大升力系数与试验雷诺数下预测值相差不大，但明显低于飞行雷诺数下的计算值；对于纵向力矩特性，两种雷诺数下计算所得纵向静稳定裕度相近，但较试验结果明显偏低。

2) 高速飞行状态，不同雷诺数下升力系数计算结果均与试验值吻合良好；线性段阻力系数计算结果呈现出随雷诺数增加而逐渐收敛的趋势，但其绝对量值均明显低于试验值；对于纵向力矩系数，其试验值整体上与试验雷诺数下计算结果的吻合程度更好。计算和试验所得中央翼段表面转捩位置绝对量值上略有差异，但其随雷诺数的变化规律基本一致，均随雷诺数增加逐步前移。

3) 以上结果表明，低速和高速风洞试验所采用的试验雷诺数尚未完全进入“自准区[24]”范围。考虑到该验证平台尺寸较小，且试验与计算气动力结果在大部分情况下吻合良好，因而在未进行变雷诺数风洞试验的前提下，利用变雷诺数CFD计算结果辅助进行风洞试验数据外推修正有助于获得较为合理的修正结果。

4) 雷诺数的改变会导致流动中惯性和黏性影响的占比以及边界层特性发生变化。雷诺数对于低速升力和失速特性的影响主要在于其改变了边界层的厚度和发展速度；而雷诺数对于高速翼面转捩位置的影响则在于流动中黏性力占比的相对变化改变了边界层流动对于扰动的抑制能力。

文中基于CFD结果开展了验证机高低速状态试验气动力数据的修正，预测的飞行状态气动力结果反映出了雷诺数效应的具体影响，具备一定的合理性。文中的研究工作也进一步表明CFD计算所得到的规律能够帮助飞机设计人员在飞行验证之前更加清晰的了解和认识验证平台真实的气动性能，从而为飞行试验的设计提供数据支撑。