小展弦比飞翼标模跨声速横向失稳运动

张杰，李王斌，王争取，潘金柱，卜忱

1.航空工业空气动力研究院，沈阳 110034

2.航空工业空气动力研究院高速高雷诺数气动力航空科技重点实验室，沈阳 110034

在未来空战的无人化、隐身化、智能化、精准化和轻量化发展趋势下，飞翼布局应运而生[1]。该类飞行器隐身能力强，有效装载大，气动效率高，与常规布局飞机相比性能上有明显的优势。国外针对飞翼布局开展了大量的研究[2-6]，以B-2为代表的大展弦比飞翼布局飞行器的研制成功是飞机设计理念的一场技术革命，随着电传控制技术及放宽稳定性设计技术逐渐成熟，适用于亚、跨声速的中等展弦比飞翼布局飞行器呈现井喷式发展，具有代表性的验证型号有美国的X-45系列、欧洲的“神经元”、英国的“雷神”、俄罗斯“鳐鱼”等，为了更加突出高速隐身及机动作战能力，提出了小展弦比飞翼布局，其不仅继承了飞翼布局的优良性能，还在续航能力、平飞加速、快速跃升等方面极为有效，使其成为了新一代战斗机研制的重要平台[7-11]。

然而，小展弦比飞翼布局飞行器的研制也存在巨大的挑战，主要体现在操稳特性及飞行控制等方面[12-13]。为提高气动性能、改善隐身特性，飞翼布局飞行器取消了平尾和垂尾，使其失去了纵向和航向的主要安定面与偏转控制操纵面，会引起稳定性缺失和操纵性能不足的问题。如纵向受扰后可能会迅速上仰，甚至失速；横向在低亚音速大迎角和跨声速中小迎角飞行状态下可能会由于分离涡非对称破裂而诱发机翼摇滚运动；航向的静不稳定和非常小的偏航阻尼会导致开环荷兰滚模态特性很差，以致于其闭环荷兰滚模态特性严重依赖于飞控系统的调节效果；大迎角下，横航向静不稳定性进一步增强，横航向受扰后可能会迅速滚转发散，甚至进入尾旋。

可见，小展弦比飞翼布局的稳定性问题是尚需解决的重要环节，由于其与大后掠三角翼有着高度的几何外形相似，在跨声速时同样面临发生 以机翼下落和机翼摇滚为主要形式的动态失稳现象[14-19]，而跨声速流场的非定常性、激波/旋涡干扰使其横向失稳运动更为复杂。针对小展弦比飞翼标模跨声速典型流动及气动特性的研究表明[20]：小展弦比飞翼标模在小迎角下就出现涡升力，随着迎角增加，前缘涡逐渐增强并向机翼内侧移动形成展向流动，同时激波也逐渐增强，当前缘涡与激波发生干扰而破裂时，升力突然下降而抬头力矩增加，其对小扰动极为敏感，前缘涡易出现非对称破裂，从而引发横向失稳运动。

在横向失稳运动控制方面，基于ICE(Innovative Control Effector)布局和三角翼的研究表明[21-26]：前缘不对称喷流产生的力和不对称流场共同作用可提供操纵需要的滚转力矩；垂直来流安装的导流片对涡流施加非对称激励，可以大大降低滚转振幅；此外，副翼偏转可平衡左右机翼不对称分离涡产生的滚转力矩从而达到控制自由滚转运动平衡位置的目的。这都为小展弦比飞翼标模横向失稳运动控制研究提供了依据。

介绍了航空工业空气动力研究院(下文简称为“航空工业气动院”)采用自由滚转、压力敏感涂料(Pressuse Senstitive Painting，PSP)和粒子图像测速(Particle Image Velocimetry，PIV)等风洞试验手段开展的小展弦比飞翼标模横向失稳运动研究。通过获取其跨声速条件下气动、运动和流场数据，评估其可能存在失稳运动的条件，最终在风洞中成功捕捉到了小展弦比飞翼标模机翼下落和机翼摇滚现象，并分析了其失稳运动特性，掌握了典型规律。通过流动显示、数值模拟综合手段研究了产生横向失稳运动的流动机理。此外还探索了失稳运动的控制手段，为飞行器研制提供技术支撑。

1 试验模型

研究所采用的模型见图1所示，其外形与“十二五”期间发布的小展弦比飞翼标模一致，前缘后掠角65°，后缘后掠角±47°，展弦比1.54，采用超临界翼型、直前缘和锯齿形尾缘。试验模型的比例为1∶25，在主要研究动态气动特性的本项目中，对小展弦比飞翼标模进行了放宽稳定性设计，将重心位置O调整至45%平均气动弦长(Mean Aerodynamic Chord, MAC)位置。此外，还设计了前缘襟翼、内外侧升降副翼、上下翼面扰流板、翼尖舵等气动控制舵面，用于稳定性及控制特性研究。

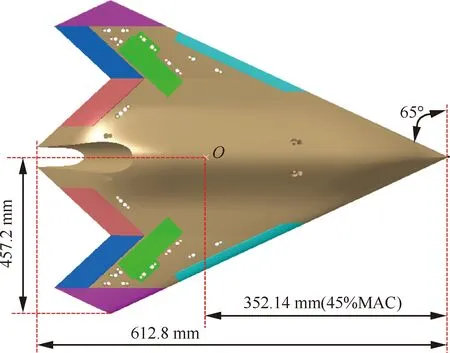
图1 小展弦比飞翼标模

2 风洞试验

在小展弦比飞翼标模跨声速横向失稳运动特性研究中，首先开展静态测力及模型表面、空间流场测量试验，获取标模在跨声速条件下静态气动及流动数据，根据静态气动力及力矩的征兆[27]，结合流场数据，分析及甄别可能出现横向失稳运动的区域，然后开展自由滚转试验，获得其滚转角历程，评估横向失稳运动严重程度和运动特性，最后针对失稳运动探索舵面组合偏转对失稳运动的控制效果。

2.1 试验风洞

试验在航空工业气动院FL-3风洞中进行。该风洞是一座直流暂冲下吹式亚、跨、超三声速风洞，试验段截面尺寸为1.5 m×1.6 m(宽×高)，亚跨声速槽壁试验段长4.2 m，上下壁是开槽壁，北侧壁及上下壁开有多个光学窗口，可进行PSP、PIV等光学试验。试验采用0#喷管和槽壁试验段，0#喷管可调马赫数范围为0.3～1.2。

2.2 气动/流动一体化测量试验

采用静态试验结合PSP、PIV手段来实现气动/流动一体化测量。静态试验即是常规测力试验，通过连续变迎角获得小展弦比飞翼标模不同状态下的纵、横向气动力及力矩。同时在模型表面喷上压力敏感涂料，以合适波长的激发光照射涂层，用滤镜分离荧光，相机采集光强信息，最后通过标定换算得到模型表面压力场。

由于迎角增大以后，模型前缘涡发展到机身后段时已离开表面变成脱体涡，在模型尾部采用PIV手段来捕捉尾流变化，在相同状态下与PSP结合，实现模型表面和空间流场的测量。PIV试验的原理见图2，标模试验照片见图3。

图2 PIV测量原理

图3 小展弦比飞翼标模在FL-3风洞PIV试验照片

PIV试验是采用脉冲激光片光光源以极小的时间间隔连续2次照亮撒播在流场中的示踪粒子，在粒子被照亮的同时用相机记录粒子的图像，采用互相关算法处理可获得两张图像对应时刻的粒子空间位移场，结合图像标定参数获得对应的空间速度场。试验中在距离模型尾缘0.15 m处布置0.3 m×0.9 m(长×宽)的片光区域，测量左右机翼前缘脱体涡的分布规律。

2.3 自由滚转试验

航空工业气动院跨声速自由滚转试验技术日趋成熟[28]，针对小展弦比飞翼标模的特殊需求，基于已有的试验装置进行了改造提升，使其具备了常规测力、自由滚转、大尺度滚转角(滚转角振幅±30°)强迫振荡等风洞试验功能，滚转角测量精度达到0.1°。采用该套试验设备进行自由滚转试验的照片见图4。

图4中，自由滚转试验的主要目的是在风洞中通过放开滚转自由度来实时测量模型在气动力激励下滚转角变化历程，采用动态品质因数pp-v评估其横向失稳运动的严重程度[29-31]；利用频谱、轨迹相图分析其运动特性[32]；最后选定前缘襟翼10°，内外侧副翼10°舵面组合偏转进行自由滚转对比试验，验证其对失稳运动的抑制效果。

图4 小展弦比飞翼标模在FL-3风洞自由滚转试验照片

3 试验结果与分析

在本研究中，开展了小展弦比飞翼标模马赫数Ma为0.6～0.95，迎角α为0°～24°，侧滑角0°范围内的静、动态气动特性，流动特性及横向失稳运动特性研究，本文展示了Ma=0.8, 0.9的研究结果。

3.1 静、动态气动特性及流动特性

小展弦比飞翼标模基本外形(舵偏角均为0°)在Ma=0.8，0.9、α=0°～24°范围内，升力系数、俯仰力矩系数、滚转力矩系数和滚转动导数试验曲线见图5和图6所示，图中还给出了“十二五”期间采用1∶19的大模型在国内3座主力高速风洞(文中简称为风洞A、B、C)的静态测力数据作为对比，可见，本文研究所用的1∶25模型D升力系数、滚转力矩系数与大模型规律一致，而俯仰力矩系数因重心改变有所不同，纵向是静不稳定的。

图5 Ma=0.8基本外形参数曲线

图6 Ma=0.9基本外形参数曲线

对研究模型，Ma=0.8、0.9时，在α=11°～16°范围内，升力系数曲线出现了斜率变小的拐折，且俯仰力矩系数曲线斜率变大；在α=10°～20°范围内滚转力矩系数随迎角变化不稳定，这都符合横向失稳运动的征兆，通过静态气动特性分析，初步筛选得到Ma=0.8、0.9,α=10°～20°条件下出可能出现跨声速横向失稳运动，但在该状态下滚转阻尼仍为负值，具备滚转动稳定特性。

Ma=0.8、0.9,α=10°～20°范围，小展弦比飞翼标模的PSP、PIV试验结果如图7和图8所示。在α=10°时标模上表面就出现低压区，这是前缘涡的主涡区域，随着迎角的增加，模型上表面的低压区位置向前移动，说明机翼后部主涡逐渐离开表面形成脱体涡。Ma=0.8,α=20°以前左右机翼前缘涡和尾流呈现对称性；α=20°时，左右机翼的前缘涡和尾涡出现明显的不对称现象。Ma=0.9时，α=15°、18°时左右机翼的前缘涡和尾涡开始不对称，但强度并不大，α=20°时左右机翼的前缘涡和尾涡不对称现象变得明显。前缘涡的不对称分离会产生附加的滚转力矩引起模型滚转，流动显示试验数据同样表明在Ma=0.8，0.9、α=10°～20°出现横向失稳运动的可能性比较大。

图7 Ma=0.8，α=10°～20°模型表面流动及尾流随迎角变化

图8 Ma=0.9，α=10°～20°模型表面流动及尾流随迎角变化

3.2 横向失稳运动特性

3.2.1Ma=0.8试验结果分析

Ma=0.8时，α=5°～20°的自由滚转试验结果如图9和图10所示。模型在α=5°释放模型后迅速发生偏转，建立动态平衡，其平衡滚转角φ随迎角增加绝对值增大，在-25°～-31.6°之间变化，这说明小展弦比飞翼标模对小扰动极为敏感，模型的几何不对称，小的气流偏角等都可以引起模型的偏置。

图9 Ma=0.8，α=5°～19°模型滚转角随时间变化

图10 Ma=0.8，α=20°模型滚转角随时间变化

在迎角变化过程中，α=15°时出现了小幅度的机翼摇滚运动，滚转角φ振幅在10°以内，随着迎角的增大运动被抑制，这与其滚转阻尼增加有关。当α达到20°时，在-28.6°平衡滚转角位置进行间歇性机翼摇滚振荡，滚转角φ振幅达到时27°，振荡频率在8～14 Hz范围，为宽频振荡。图11 和图12为α=15°和α=20°模型运动轨迹相平面图其中,ωx为滚转角速度。可见，在α=15°的横向失稳运动属于混沌，在α=20°的横向失稳运动属于多周期。

图11 Ma=0.8，α=15°的运动轨迹相平面图

图12 Ma=0.8，α=20°的运动轨迹相平面图

从图13的动态品质因素Pp-v评估结果分析，α=15°的横向品质因素略超过临界值0.002，飞行品质未明显变差，而α=20°时横向飞行品质明显变差。由此可见，Ma=0.8，α=20°属于以机翼大幅摇滚运动主要形式的横向失稳运动，并引起了飞行品质的恶化。

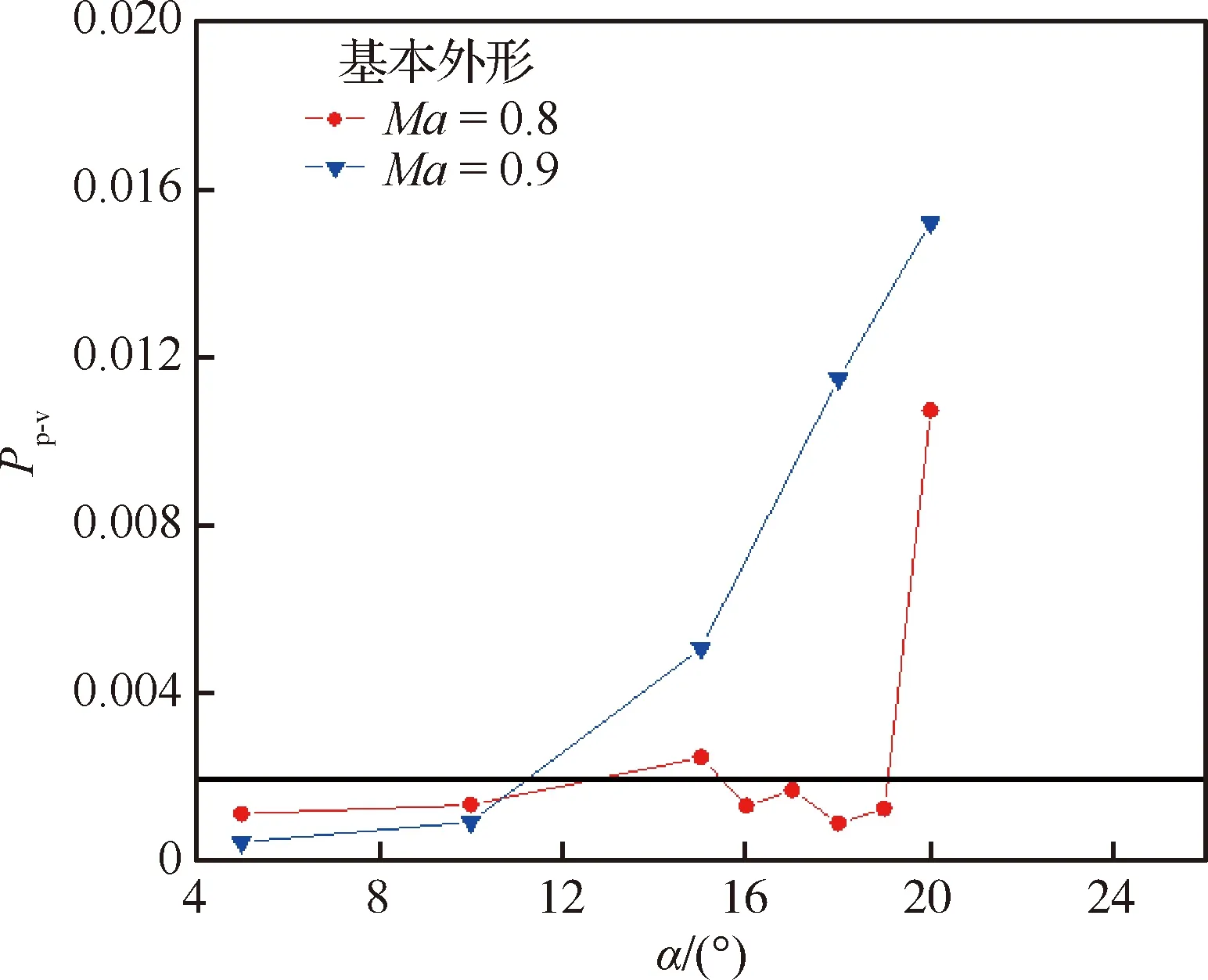
图13 Ma=0.8、0.9,α=5°～20°范围Pp-v评估结果

3.2.2Ma=0.9试验结果分析

在Ma=0.9，α=5°～20°的滚转角变化历程如图14所示，在α=5°时释放模型，在迎角10°前模型未出现明显偏转，平横滚转角在-10° 以内，迎角增大至15°时，出现了机翼下落和小幅机翼摇滚振荡，滚转角φ振幅在8.5°以内，因滚转阻尼的作用在很短的时间内被抑制，未进入振荡模态。迎角10°～20°变化过程中，平衡滚转角绝对值逐渐增大，α=18°，20°时，平衡滚转角达到-45°左右，且出现了大幅度机翼摇滚运动，α=18°时滚转角振幅在22.5°，α=20°时滚转角振幅达到30°，振荡频率在8～14 Hz范围，为宽频振荡，且随着迎角增加，振荡主频逐渐增大。图15 和图16为α=18°和α=20°时模型运动轨迹相平面图，可见，α=18°，20°的横向失稳运动均为多周期。

图14 Ma=0.9，α=5°～20°模型滚转角随时间变化

图15 Ma=0.9，α=18°的运动轨迹相平面图

图16 Ma=0.9，α=20°的运动轨迹相平面图

从图13的Pp-v评估结果分析，Ma=0.9，在α=15°～20°范围内，横向品质因素均超过0.002的临界值，飞行品质变差，其中α=15°是以机翼下落为主的横向失稳运动，α=18°，20°是以机翼摇滚为主的横向失稳运动。

3.3 舵面组合偏转对失稳运动控制效果研究

在跨声速风洞试验中，采用喷流、扰流片等主动流动控制方式来实现横向失稳运动的抑制较为困难，以组合舵面对模型稳定性影响数据为依据，结合前缘襟翼和副翼下偏有抑制流动分离和减缓激波强度的理论基础，分析选取了前襟偏转10°、内外侧副翼同时偏转10°组合，开展自由滚转风洞试验验证其对失稳运动的控制效果。

试验选取横向失稳运动比较严重的状态，即Ma=0.8、0.9,α=20°。自由滚转试验结果如图17和图18所示。Ma=0.8，α=20°时，前缘襟翼、内外侧副翼组合偏转时模型并未发生机翼摇滚运动，说明在该状态下组合舵面偏转起到了抑制摇滚运动的作用；而Ma=0.9，α=20°时，前缘襟翼、内外侧副翼组合状态仍然出现了机翼摇滚运动，其运动振幅与基本状态基本一致，说明在该状态下舵面组合偏转未起到抑制机翼摇滚运动的作用。

图17 Ma=0.8， α=20°舵面组合偏转与基本状态滚转角随时间变化

图18 Ma=0.9，α=20°舵面组合偏转与基本状态滚转角随时间变化

通过不同马赫数的对比试验可知，舵面组合偏转是可以起到改善横向失稳运动作用的，但并非所有的马赫数都适用于同一种舵面组合偏度，可进一步探索不同马赫数下不同舵面偏转组合的影响，获得一般规律。

4 跨声速横向失稳流动机理研究

采用基于混合LES/RANS高阶湍流(Detached Eddy Simulation, DES)模拟的数值方法对失稳运动过程的流动开展机理研究。为了控制数值离散过程中的格式耗散和色散，提升分离区域的模拟精度，在空间离散方向采用高阶插值的总变差减小格式(Total Variation Diminishing, TVD)，时间方向采用隐式非定常双时间步格式。

流场变量存储使用格点格式，网格表面单元为三角形，空间单元为四面体和三棱柱混合形式。物面为无滑移绝热物面边界，进出口使用远场条件。

计算采用有限体积法对亚跨声速流动进行数值模拟，三维Navier-Stokes (N-S)方程为

(1)

式中：Q为常数项；F1、F2、F3,G1、G2、G3分别为无黏和黏性通量矢量；S为源项矢量。

非定常计算时，初场使用定常场，模型姿态固定，非定常物理时间步长为0.000 05 s，计算时控制内迭代步数使内迭代残差下降一个量级。计算网格见图19，全模总的空间网格数约4 000万单元。

图19 模型表面及对称面网格分布

图20给出了Ma=0.85，不同迎角下模型的空间涡结构变化过程，图21是采用DES方法计算的Ma=0.85，不同迎角下模型滚转力矩随时间变化。

图20 Ma=0.85，α=10°～20°模型空间涡结构变化

图21 Ma=0.85，不同迎角下滚转力矩随时间变化

CFD的研究结果表明：跨声速条件下出现横向失稳运动时，小展弦比飞翼标模流动十分复杂，主要表现为机头、机身部位多道激波形成复杂波系；机翼前缘形成的主涡随迎角增加变化复杂，旋涡与激波的相互作用对涡破裂与分离产生影响，进入激波系统的涡是不稳定和脉动的；大迎角时流场的不对称性和非定常性明显。模型的自激滚转运动是由于机翼前缘涡的分离不对称导致的。前缘涡在模型升力系数曲线出现拐折前呈现整体附着的细长涡，迎角增加后，前缘涡沿程涡核高度、涡宽度增加，能量增强，这时涡核靠近机身对称面，但是沿涡核方向向下游的补充能量不足以维持涡的发展，在涡核速度降为0后，出现涡破裂。涡破裂后低频涡之间又相互干扰并发展，低频伴随更高频的振动使滚转力矩曲线高低频共存，造成模型两侧滚转力矩的不对称，表现为正负振荡的滚转力矩，且能量较强。迎角继续增加后，低频涡脱落位置提前，频率增加，使模型滚转力矩变化频率相应增加。跨声速情况下，迎角增加后，背部激波强度增加，激波位置向前移动，涡破裂与激波相互干扰，导致左右机翼的涡破裂区域变大，不对称性增强，非定常变化的滚转力矩造成了模型滚转周期性自激振荡。

5 结 论

通过对小展弦比飞翼标模跨声速横向失稳运动的综合研究，得到如下结论：

1) 综合采用气动/流动一体化测量、自由滚转风洞试验建立的系统评估手段对研究跨声速横向失稳运动具备可靠性。

2) 可能出现横向失稳运动的区域，在静态气动力上会出现征兆，可对研究范围的筛选提供依据。

3) 在风洞中捕捉到的Ma=0.8，α=20°和Ma=0.9，α=15°、18°、20°条件下的横向失稳运动是以机翼下落和机翼摇滚为主要运动的形式，动态品质因素分析表明失稳运动直接导致了横向飞行品质变差。

4)Ma=0.8、0.9条件下，小展弦比飞翼标模的横向失稳运动特性是混沌或多周期的宽频振荡，且振荡主频随着马赫数和迎角的增大逐渐增大。

5) 舵面组合偏转可以改善小展弦比飞翼标模的横向失稳运动特性，但不同的马赫数对舵偏组合的要求不同，需进行系统研究，获得一般规律。

6) 在跨声速失稳运动发生区域，流场的不对称性和非定常性明显，导致了左右机翼分离的不对称，产生的滚转力矩高低频共存，造成了模型滚转周期性自激振荡。