基于机器学习的山西省人间布鲁氏菌病的预测研究
张珍珍,阮若楠,苑宏泽,张 龙
(太原学院 计算机科学与技术系,山西 太原 030032)
0 引言
布鲁氏菌病,简称布病,是一种由多种布鲁氏杆菌引起的人畜共患病[1],被世界动物卫生组织列为必须通报的传染病,在中国被列为乙类传染病。人感染布病之后主要的临床表现为体热、多汗、关节疼等症状,轻重不一,大多数患者常伴有淋巴结、肝、脾肿大等症状[2]。2000年以后,布病成为我国报告发病数量上涨速度最快的传染病之一。以山西省为例,2010年报告的人间布病发病率为10.88/10万,之后逐年增多,到2014年时达到顶峰23.53/10万。随着国家和地方对布病防控措施的增强,2014-2017年间人间布病发病率急剧下降至1.24/10万。但是从2018年至今,有逐步回升的趋势,2020年人间布病发病率为3.29/10万。近年来山西省的病例数呈上升趋势,且流行性强,范围广,因此该地区的布病防控工作尤为重要[3]。
流行病学多年研究表明,诸如温度、湿度和风速等气象因素会对传染病的发病率产生促进或抑制作用。最近的一些研究使用了时间序列模型证实了在时间维度上持续变化的气象因素确实对传染病的发病率产生了影响。例如,HUANG等人利用广义加性模型分析了气象因素对手足口发病率的影响[2]。GOTO等人将线性回归模型与向量自回归(VAR)模型相结合,研究每周的平均最高气温及总降雨量与登革热发病率之间的联系[4]。我国已有许多学者运用泊松回归分析、格兰杰因果关系分析和自回归分布滞后模型分析了2004-2010年人间布鲁氏菌病的发病情况,结果表明对于冬季和春季布鲁氏菌病的局部爆发与气温偏低和日照时数偏少有关[5]。
由于山西省的人间布病月发病率的变化是非线性的,而机器学习模型善于处理复杂的非线性问题。因此选用支持向量机、随机森林、深度神经网络等3种机器学习模型,以多种不同的气象因素作为预测变量探索适合于布鲁氏菌病发病趋势的拟合统计模型,使其能够快速、低误差地预测布病的未来发病趋势,以达到早期预警的目的,为政府制定布病预防策略提供支持。
1 材料与方法
1.1 研究数据
1.1.1山西省布鲁氏菌病的发病数据
山西省人间布鲁氏菌病的月病例数来自于山西省疾病预防控制中心。
1.1.2山西省气象资料
山西省每月气象数据来源于中国气象数据网。这里选择了6种气象数据,分别是月平均气温、月平均总降水量、月平均相对湿度、月平均大气气压、月平均风速以及月平均日照时数,它们的基本信息和度量单位如表1所示[6]。

表1 气象因素的基本信息Tab.1 Basic information of meteorological factors
1.2 机器学习模型
1.2.1支持向量机模型
支持向量机(support vector machine,SVM)最近在机器学习和模式分类领域取得了突出的地位。分类是通过在输入空间中实现线性或非线性分离面来实现的。
在支持向量机的分类中,分离函数通常表示为与支持向量相关的核函数的线性组合,如式(1)
f(x)=∑xj∈SαjyjK(xj,x)+b
(1)
其中:xj表示训练模式;yj∈{+1,-1}表示相应的类标签;S表示支持向量集。
1.2.2随机森林模型
随机森林(random forest, RF)是一种被广泛使用的集成方法,它构造了许多决策树,用于通过多数投票对新实例进行分类。每个决策树节点使用从整个原始属性集中随机选择的属性子集。此外,每棵树都以与装袋相同的方式使用不同的引导样本数据。其定义为:它是一个由树结构分类器 {hk(X,Tk)},k=1,2,3,…,L,集合组成的分类器,其中Tk表示完全独立分布的随机样本,每棵树在输入X处为某类别投票。
1.2.3深度神经网络模型
深度神经网络(deep neural network,DNN)主要分为输入层(X)、隐藏层和输出层(Y),其模型结构示意图如图1。第一层是输入层,将特征值作为该层的输入,其中神经元节点数等于特征的数量,最后一层是输出层,该层的神经元节点数取决于输出目标的数目,中间部分为隐藏层,隐藏层的数量会根据现实数据的拟合情况设计,相邻两层之间的神经元相互连接,其神经元由连接权值(w)、激活函数(g(z) )以及偏置值(b)组成,其表达式如式(2),(3)

图1 深度神经网络的结构示意图Fig.1 Structural diagram of DNN
(2)
a=g(z)
(3)
其中:n表示特征变量总数;wi表示第i个特征变量的权值;xi表示第i个特征变量;b表示偏置值;a为神经元节点的输出。
1.3 模型评估
本次研究主要采用的模型评价指标为:均方误差和平均绝对值误差。
均方误差(英文简称MSE),指的是预测值与真实值之间距离的平方和,其表达式如式(4)
(4)
平均绝对值误差(英文称简MAE),指的是真实值和预测值之差的绝对值之和,其表达式如式(5)
(5)
MSE对异常值敏感,如果样本中存在离群点,MSE会给离群点赋予更高的权重;而MAE因为没有平方项的作用,惩罚力度都是一样的,因此对离群点的敏感度较低,更有包容性。
2 结果
2.1 山西省气候特征及人间布病月发病情况
2.1.1山西省气候特征
山西地处中纬度,属于暖温带、温带大陆性气候。2010-2020年每月平均气温为9.348 ℃,最低平均气温为-9.940 ℃,最高气温为23.88 ℃,跨度相对较大。月平均总降水量为0.002 m,降水量稳定适中。月平均相对湿度、月平均大气压力、月平均风速的中位数分别是51.15%,887.191 hPa,2.404 m/s。月日照时数最大值与最小值差异较大,分别为332.39 h和87.60 h。气象因素的具体信息如表2所示。

表2 2010-2020年山西省气象因素统计描述Tab.2 Statistical description of meteorological factors in Shanxi Province from 2010 to 2020
2.1.2山西省布鲁氏菌病的月发病情况
山西省2010-2020年人间布鲁氏菌病发病率的时间序列如图2所示。从图2可以看出,人间布病发病率从2月开始显著增多,直到5月达到最高值,之后缓慢下降,人间布病的高发期主要集中于3-7月[7]。
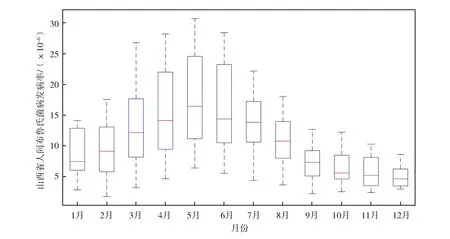
图2 2010-2020年山西省人间布病发病率时间分布Fig.2 Temporal distribution of the incidence of human brucellosis in Shanxi Province from 2010 to 2020
2.2 山西省气象因素与人间布病发病率的关联研究
山西省2010-2020年每月人间布鲁氏菌病发病率与气象因素之间的关系,通过斯皮尔曼等级相关方法计算可得,二者之间的相关系数如图3所示。图3中,颜色越深表示发病率与气象因素的关系越强。大气压力与发病率的相关系数分别为-0.63,表示大气压力与发病率呈现负相关性,且绝对值最大,意味着关系最强。温度、日照时数、总降水量与发病率的关系较强,相关系数分别为0.43、0.43、0.33,表示它们与发病率呈正相关。另外3个气象因素与发病率仍具有统计学意义,全部气象因素均可当作人间布病发病率预测的输入特征变量。
此外,由图3可得,各种气象因素之间或强或弱的相关性将导致它们之间的共线性问题。机器学习模型可以消除输入特征变量之间的共线性,故选取机器学习模型作为人间布病发病率预测的模型。
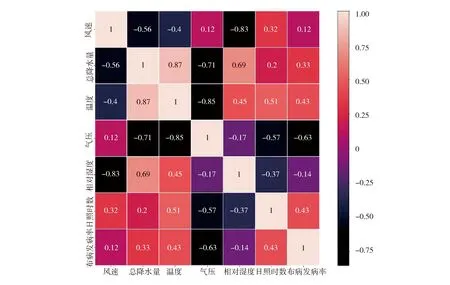
图3 气象因素与山西省人间布病发病率斯皮尔曼相关系数热图Fig.3 Heat map of Spearman correlation coefficient matrix between meteorological factors and human brucellosis incidence in Shanxi
2.3 机器学习模型
本研究数据集为2010-2020年山西省人间布病月发病率以及月气象因素数据。首先,因为数据量偏小,仅将数据分为训练集和预测集。训练集选择2019年12月-2020年1月的数据,2020年的月数据作为预测集。
所有数据存在量纲不尽相同的问题,因此在模型训练前先通过特征缩放法将所有数据进行归一化处理,如式(6)
(6)
2.3.1支持向量机模型
支持向量机模型中核函数采用径向基函数,同时使用网格法和10-折交叉验证进行参数调整以得到最优化的模型。此时c(惩罚系数)= 1,g(gamma参数)= 0.7,模型的误差最小,拟合效果最好。训练集的MSE为24.092,训练集的MAE为3.189,预测集的MSE为8.786,预测集的MAE为2.532。支持向量机模型最优预测模型如图4所示。
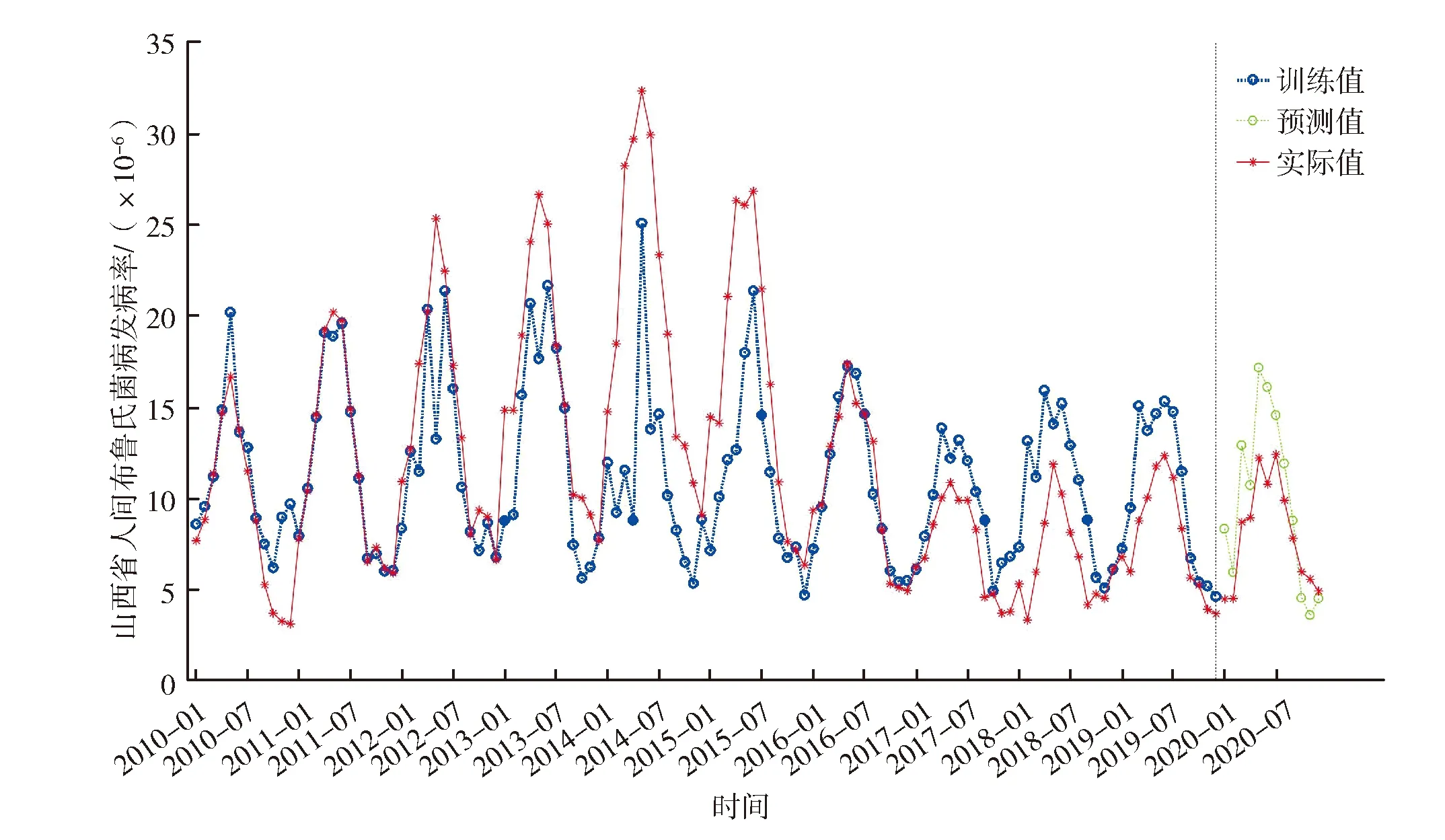
图4 支持向量机的最优模型 Fig.4 Optimal model of SVM
2.3.2随机森林模型
随机森林模型中重要的参数有n_estimators(随机森林中决策树的个数),max_depth(决策树的最大深度),min_samples_leaf(叶子节点含有的最少样本数),min_samples_split(节点可分的最小样本数)。当调整参数为n_estimators=120,max_depth=8,min_samples_leaf=4,min_samples_split=5时,模型的误差最小,拟合效果最好。训练集的MSE为6.210,训练集的MAE为1.783,预测集的MSE为12.126,预测集的MAE为2.529。随机森林模型的最优预测模型如图5所示。

图5 随机森林模型的最优模型 Fig.5 Optimal model of RF
2.3.3深度神经网络模型
深度神经网络模型中,通过不断调试后最终确定网络结构为6-13-9-1,即输入层为6种气象因素的特征变量,节点数为6,第一、二层隐藏层的节点数依次为13和9,输出层为布病发病率,节点数为1。激活函数均采用Relu函数,优化方法选用随机梯度下降,学习率设为0.008,动量设为0.9,权重衰减设为1×10-4,每次训练的样本数设为120。这时的训练集MSE为16.890,MAE为3.095,而预测集MSE为11.421,MAE为2.943。很好地平衡了拟合效果和预测效果,深度神经网络模型的最优预测模型如图6所示。
图6 深度神经网络的最优模型 Fig.6 Optimal model of DNN
2.3.4结论
本次研究采用的是定量预测,建立支持向量机、随机森林和深度神经网络3种模型预测山西省人间布鲁氏菌病的发病率,通过MAE值和MSE的值来分别评价各个回归模型的性能及误差,最后采用平均相对百分误差进行3种模型的横向对比,如表3所示。3种机器学习模型得到的预测值与2020年每月发病率的真实值之间的误差较为接近,且均表现出较好的预测效果,以随机森林模型最优,具有最高的预测精度。同时也证明了可以利用机器学习对布鲁氏菌病与气象因素之间的关系进行分析,进而对人间布鲁氏菌病的早期预警和制定防控措施提供科学依据。
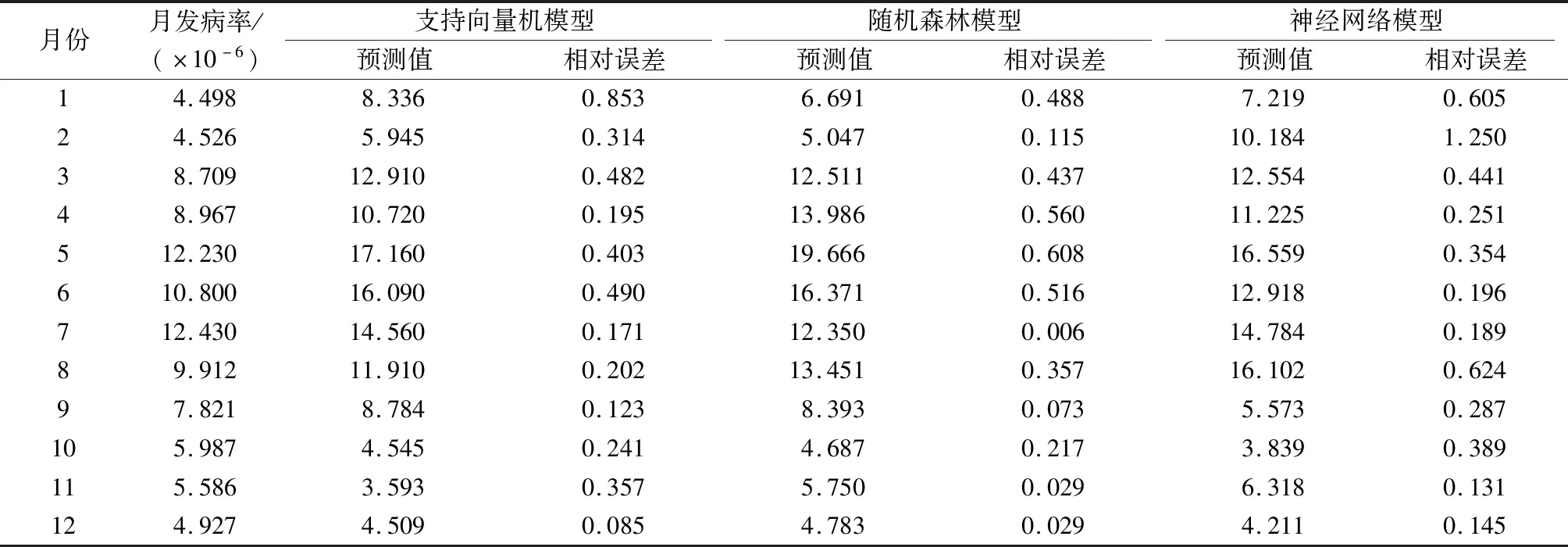
表3 3种机器学习模型平均相对百分误差比较Tab.3 Comparison of average relative percentage errors of the three machine learning models
3 讨论
总之,机器学习模型能挖掘气象因素与布病发病趋势复杂的关系,从而通过气象因素预测布病发病趋势,该预测模型的建立可以为进一步探究未来人类布病发病率的时间分布提供有效的工具。建议防治部门在每年3-7月,也就是布病的高发期增大防控力度,对大同、晋中等布病高发区的畜产品做好检疫工作,从根源处断绝布病的传播;同时加强对牛羊养殖户的管控,避免出现倒卖染病牛羊等情况,做好对于染病牛羊的补偿工作,并加大对布病危害的宣传力度。

