印度洋海表盐度预报的线性马尔可夫模型及其改进办法
吕泓柯, 巩远发, 王桂华
1. 成都信息工程大学大气科学学院, 四川 成都 610225;
2. 湖南省人工影响天气领导小组办公室,湖南 长沙 410118;
3. 气象防灾减灾湖南省重点实验室,湖南 长沙 410118;
4. 复旦大学大气与海洋科学系, 上海 200438;
海洋表面盐度(sea surface salinity, SSS)和海洋表面温度(sea surface temperature, SST)是海洋表面的基本物理状态, 在水循环、海洋环流、海洋生态系统乃至天气和气候变化等方面都发挥着至关重要的作用(Lin et al, 2001)。
相比SSS, 人们对SST 的研究深入得多。SST的观测技术发展相对较长, 目前国际上有多种较为完整的SST 产品 (Guan et al, 2003; Thiébaux et al,2003; Reynolds et al, 2007; Woodruff et al, 2011;Donlon et al, 2012), 其应用也相当广泛和成熟(Srivastava et al, 2000; Guo et al, 2004; Zhan et al,2011)。然而, 受观测资料的限制, 盐度的研究则相对较为匮乏。在20 世纪末Argo 计划实施前, 全球海洋每年的盐度观测数据只有温度的15%左右。Argo 计划实施后, 对海洋盐度的观测能力得到极大提升, 至2005 年左右, 每年的盐度观测数量与温度基本相当(王辉赞 等, 2012)。进一步, 随着海洋盐度卫星 SMOS(Soil Moisture and Ocean Salinity)、SAC-D(Scientific Application Satellite-D)等的成功发射, 逐渐积累了一定量的盐度数据, 这为开展盐度方面的研究乃至预报工作提供了极大保障。
印度洋作为印—太暖池的重要组成部分, 对我国天气和气候所起的作用被广泛关注。印度洋是印度季风的发源地和流经地, 印度季风是亚洲季风的主要成员, 而印度洋的变化能通过影响具有行星尺度的亚洲季风系统在中—高纬度的相互作用来影响中国天气气候的异常变化(晏红明 等, 2000)。海洋上层盐度对天气过程、季节内振荡以及季节与年际等更为低频的海气耦合模态, 都有重要的反馈作用(Qiu et al, 2012)因此, 开展印度洋SSS 的预报工作,对预报预测中国天气气候具有一定的指导意义。
现有海洋模型HYCOM、MOM、NEMO、ROMS和POM 等, 可以对全球海洋进行模拟预报(方长芳等, 2013)。但是, 多变量经验正交函数(multi-variate empirical orthogonal function, MEOF)和线性马尔可夫相结合的预报模型(简称线性马尔可夫模型, 下同)凭借着计算便捷, 开发成本低且预报效果好等因素,被广泛应用于各种海洋要素的预测, 如太平洋海表温度异常(Johnson et al, 2000)、南极海冰(Chen et al,2004)、ENSO(Xue et al, 1994)、东亚季风降水变化(Wu et al, 2013)等。尚未发现利用该模型对盐度进行预测的研究, 故本文尝试将线性马尔可夫模型初步应用于印度洋SSS 的预测, 从混合层盐度收支方程出发, 选择海表面高度(sea surface height, SSH)、SST、SSS 等物理量的异常值作为模型的组成部分,对印度洋SSS 进行逐月预报, 并进一步考虑遥相关关系, 提高线性马尔可夫模型的预报能力。
1 资料与方法
1.1 资料介绍
基于盐度方程进行物理量的选择。由于模式是在MEOF 的基础上构建的, 因此需要考虑大气、海洋动力学和热力学因素对SSS 变化的作用, 故我们根据混合层盐度收支方程(Foltz et al, 2004)选择物理量。
除了SSS 可以明显地影响自身变化以外; SSH也可以通过影响海洋水平速度进而影响SSS; 再者,海温也可以通过影响大气环流和降水来间接影响SSS。基于此分析, 本文选用的资料包括: 来自Argo项 目 (http://apdrc.soest.hawaii.edu/las/v6/constrain?var=204)的月均SSS 数据, 格点为1°×1°。月均SSH数据来自哥白尼海洋环境监测服务中心 (center for marine environmental monitoring service, CMEMS)(https://marine.copernicus.eu/), 并插值到 0.5°×0.5°的网格上。1°×1°分辨率的SST 数据由美国国家环境预测中心(National Center for Environmental Prediction, NCEP)(https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html)提供。此外, 方程中包含的蒸发、降水等物理量, 因对预报效果改善并不明显(详见3.1), 这里一并略去。最后, 参与模型构建的时间尺度选择2005—2017 年, 模型使用的区域覆盖了印度洋地区(40°S—30°N, 30°E—110°W)。
1.2 线性马尔可夫模型构建
关于线性马尔可夫模型构建细节(Chen et al,2004)大致分为以下几个步骤:
1) 计算各变量的逐月异常值, 即各变量减去各月在13 年(2005—2017 年)内的平均值, 并分别归一化。再将上述各异常值保持时间尺度不变, 并在空间上进行累加, 组合成一个时间和空间的二维数组。
2) 将这个数组进行MEOF 分解:

式中,V为进行MEOF 分解的数据矩阵,E和P分别为MEOF 分解后所得到的空间模态和相应的时间序列,T为矩阵转置符号。
3) 将时间序列按月拆分。假设相邻的PC 之间存在线性关系, 计算自然月间的马尔可夫过渡矩阵A:
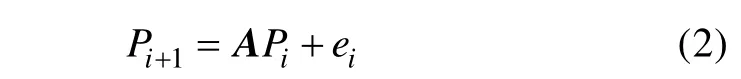
式中,Pi和Pi+1分别为第i个月、第i+1 个月的时间序列,ei为误差。从上式得到
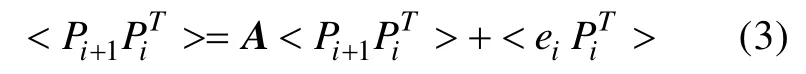
式中, 尖括号表示时间平均, 对于最优的模型配置来说误差ei与PT i线性无关, 故转移矩阵A为:
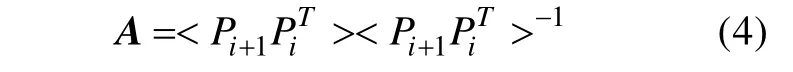
由上式得到的转移矩阵一共有12 个, 即1 月与2 月, 2 月与3 月……12 月与翌年1 月间的过渡矩阵。
4) 保留适当的模态, 通过依次应用马尔可夫过渡矩阵预测时间序列, 并将相应的预测值与各自的空间场相结合, 最终达到对所选变量预测的目的。
1.3 统计方法
本文主要运用统计学的方法来衡量模式预报结果的优劣性, 包括均方根误差(RMSE)和相关系数(r)。其中均方根误差是真实值与预报值之间的偏差,用于衡量模式结果的准确度。相关系数则是反应观测值与预测值之间相关关系的密切程度。设X(ii= 1,2, …,n) 为预报值,Yi(i= 1,2,… ,n)为相应的观测值。和σ X(σY)分别为X i(Yi)的平均值和标准差, 有如下的统计关系:

1.4 基于遥相关物理量的选择
传统线性马尔可夫模型总是选择同一区域的物理量进行构建, 本文一开始对印度洋盐度预报模型的构建亦是如此, 但实际影响印度洋SSS 的物理量远不止于此, 比如太平洋可以通过印度尼西亚输运量(Indonesian throughflow, ITF)(刘凯 等,2011)、印度洋偶极子(Indian Ocean Dipole, IOD)(Saji et al, 1999)、热容量和海洋罗斯贝波等对印度洋产生影响(李雁领 等, 2004; 王健 等, 2014)。所以我们需要考虑遥相关关系, 即向该模型里加入不属于同一区域但相关联的物理量, 提高模型的预报水平。
1.5 主要的变化模态
为合理预估保留的MEOF 模态数, 我们首先分别对各个物理量的异常值进行EOF 分解并计算其方差贡献率。图1 分别为印度洋区域海表面高度异常(sea surface height anomaly, SSHA)和海表面温度异常(sea surface temperature Anomaly, SSTA)以及海表面盐度异常(sea surface salinity anomaly,SSSA)在EOF 分解后的方差贡献分布情况。当EOF模数大致小于 5 时, 所有物理量的方差贡献率都较大, 反之方差贡献率相对较小。这表明前几个模态就能强烈地捕获这些参数的主要信息。因此, 在后续的工作中, 我们只需要为该模型保留 5 个左右的模态。
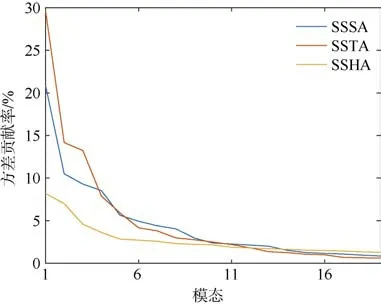
图1 各物理量在不同EOF 模态上的方差贡献分布图Fig. 1 Distribution diagram of the variance contribution of the EOF
MEOF 方法是常用的包含多个气象要素场的分析方法, 图2 便是由SSS、SST 和SSH 组合而成的数组在前三个模态的空间变化。前三模态方差贡献率分别为13.2%、8.6%和5.9%。第一模态里, SSS随纬度的分布呈带状变化, 正值极区位于印度洋北部, 负值极区位于印度洋中部, 随后在印度洋南部呈现偏正的特征。在第二模态中, SSS 存在反相变化的偶极模式, 并呈现东西分布的状态, 这与第二模态的SST 空间场较为相似。最后, 在第三模态中,SSS 空间场在大部分海盆内都呈现了偏负值的情况,而SSH 空间场的绝大部分海域在前三个模态也呈现负值。故在模型中加入SSH 和SST, 能更好地模拟印度洋SSS 的空间变化。
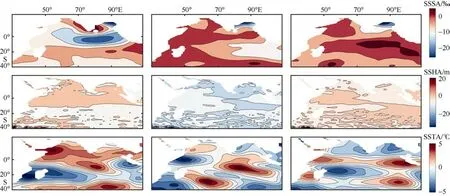
图2 由SSS、SSH、SST 组成的数组进行MEOF 分解得出的前三模态的空间场Fig. 2 First three MEOF modes of the combined SSS, SSH and SST
2 模型结果
2.1 后置预测
首先使用非交叉验证方法来讨论线性马尔可夫的后置预测模型, 这是一种不破坏数据连续性的方法。为使结果差异明显, 我们先对每一个网格点随时间变化的基础上求得相关系数, 再进行区域平均(下同)。基于上述讨论的结果, 保留前3、5、7 个模态数, 提前0~12 个月预测场与观测场之间的区域平均相关性如图3 所示(其中每个点的相关系数都通过了显著性检验, 下同)。在大部分提前时间范围内,保留模态数越多, 预测效果越好, 所以这里讨论保留前7 个模态的模型。同时, 本文以相关系数r=0.5为参考,r>0.5 代表较好的预报,r<0.5 则代表不理想的预报。如图3a 所示, 如果实验中只包含SSSA, 大致可提前6 个月在印度洋进行海表盐度预报。如果考虑加入SSTA(图3b)或者SSHA(图3c), 提前8 个月的预报效果也是较好的。包含SSHA 或SSTA 的模型似乎显示了更多与原始场相匹配的细节, 这可能是因为海洋包含了系统的大部分信息。最后, 当我们添加了SSSA、SSHA、SSTA(图3d)之后, 改善效果更为明显, 甚至可提前9 个月进行印度洋海表盐度的预报。
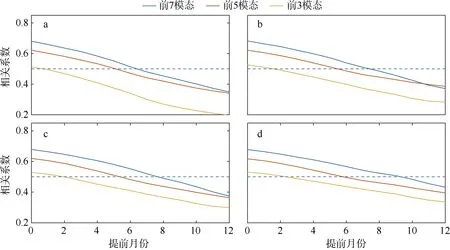
图3 预测和观测SSSA 的相关性折线图Fig. 3 Line plot of non-cross-validation correlation coefficients for the predicted and observed SSA
选择适宜的物理量不是一蹴而就的, 从混合层盐度收支方程中可以发现, 还有很多物理量会影响盐度的变化, 如蒸发、降水、海表面风场等等。但如图4 所示, 这些物理量的加入并不能提高模型的预报能力, 因此后续工作中都将其舍弃。
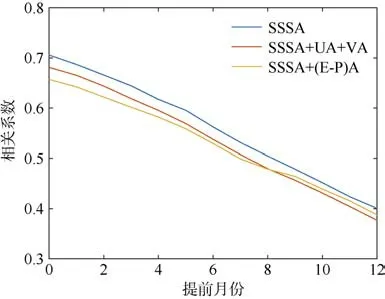
图4 预测和观测SSSA 的相关性折线图Fig. 4 Line plot of non-cross-validation correlation coefficients for the predicted and observed SSSA
2.2 交叉验证
运用交叉验证, 保留不同MEOF 模态数进行后置预测实验, 进一步探讨模型的构造。基于上述讨论, 模型的技能似乎随着保留的模态数增加而增加。但从理论上讲, 马尔可夫模型只需要保留一定数量的模态数, 因为使用太多的模态可能会有很多噪声污染模型。此外, 在上述非交叉验证的预报中存在一定人为影响, 因为该模型用于验证的数据与参与模型构造的数据是存在重叠的情况。所以我们运用交叉验证的实验来解决上述问题, 一般方法如下: 首先, 对多变量矩阵进行MEOF 分解, 得到对应的空间模态和时间序列(步骤只做一次); 再对每年的PC 进行一一验证, 这里设定用于验证的数据是时间范围为1 年的PC 数据, 用于验证的PC 从头开始逐月向后, 直至时间序列的末尾, 共计156 次(13 年×12 月=156 次)。这里保留对应的物理量和一定的模态数, 建立线性马尔可夫的验证模型。图5显示保留了13 年的SSSA、SSHA 和SSTA 组合而成的样本, 在不同的模态数和预报时间基础上, 预测SSSA 和观测场之间交叉验证的相关性。我们得出, 模型预报技能并没有随着保留模态数的增加而增加, 当保留前5 个模态时, 预报效果最好。此外,印度洋区域海表盐度的后置预报技能较为可观, 即便提前8 个月, 该相关性也会在0.4 左右浮动。
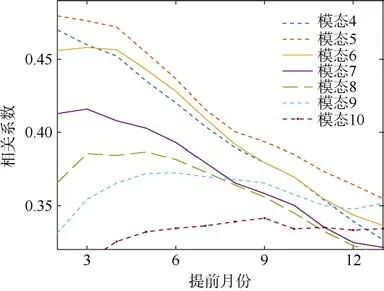
图5 后置预测和观测SSSA 之间的交叉验证相关性在印度洋地区保留不同模态数, 由SSSA、SSTA、SSHA 组合而成Fig. 5 Line plot of cross-validation correlation coefficients for the predicted and observed SSSA
为更直观的对比分析, 把仅包含SSSA 的模型和包含SSSA、SSTA、SSHA 的模型从上述交叉验证实验中得到的相关系数在空间上进行绘制。其中,所有小于0 的点都设置为0。如图6 所示, 2 个模型虽然都存在随着预报时间的增加, 预测效果变弱的情况。但是, 即使提前预报时间较长(如图所示提前9 个月), 模型所拥有的相关性较好的区域(红色区域)也相当多, 这说明该预报模型是可行的, 甚至在部分区域的预测效果是很好的。此外, 包含SSSA、SSTA 和SSHA 的模型预测结果较好的区域是完全大于仅包含SSSA 的模型, 这也进一步说明了多元成分模型的优越性。
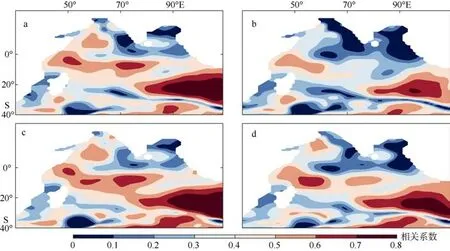
图6 后置预测与观测SSSA 的相关系数空间分布图Fig. 6 Spatial distribution of cross-validation correlation coefficients for the predicted and observed SSSA
综上所述, 通过上述各种关于模型构造的讨论,我们将保留SSSA、SSTA、SSHA 和前5 个模态, 进行后续预报实验。
2.3 考虑遥相关关系和相关系数的最佳预测解决方案
为提高预报效果, 有必要对传统模型进行改进。由于传统模型仅由同一区域的部分物理量进行构造, 但是影响该区域物理量(预报量)的物理量远不止于此, 因此, 这里考虑向模型中添加有遥相关关系的因子。基于已确定的物理量, 特别添加南太平洋的SSHA、SSTA 以及IOD 系数(方法2), 挑选合适物理量的方式与3.1 一致, 这里不再赘述。最终基于“实时”预报的评估结果如图7 所示。为避免结果的偶然性, 我们把新“实时”预测得到的物理量(预测量)放入模型中对应物理量(观测量)的末尾,保证模型中数据时间尺度不变, 去掉前端的数据,从而构成新的模型。并一次又一次地预测得到新的量, 重复上述步骤, 直至时间序列的末尾, 最后做时间平均。从图7 可知, 当模型添加这些遥相关量以后, RMSE 明显变小, 相关系数增加。从相关系数的均值计算得出, 这样的预报效果大约提高10%。这意味着这种方法是可行的, 故下文利用改进后的模型对印度洋SSS 进行“实时”预测, 进一步检验该模型的效果。
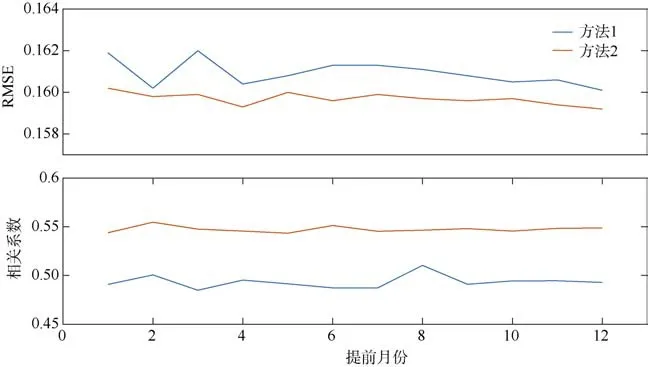
图7 观测与预测SSSA 场之间的RMSE 及相关系数Fig. 7 The RMSE and the correlation coefficients between the observed and predicted SSSA fields
3 “实时”预测的评估
所谓“实时”预测, 预测的目标周期都超过模型的训练周期。本文从2017 年12 月开始, 逐月对印度洋SSS 进行预测, 其预测效果(RMSE 和相关系数)随时间的变化如图8 所示。在预测的前7 个月内,RMSE 从0.24 降低到0.1, 相关系数从0.95 增加到0.99。不仅如此, 为比较原始数据和预测数据随时间的变化, 我们选择大洋东西分界78°E 和南北分界线赤道为断面。同时, 把HYCOM 在2008 年SSS 的逐日后置预报数据处理成逐月平均数据(https://www.hycom.org/dataserver/gofs-3pt0/analysis), 一同参与比较。如图9、10 所示, 首先, 线性马尔可夫模型预测得到的SSS 的空间分布特征与观测场较为吻合,均呈现出西高东低(图9)和南高北低(图10)的分布态势。此外, 在赤道断面, 本文模型预测的SSS 极值在冬季相对较大, 在夏季相对较小, 这与观测场随时间的变化情况是一致的, 这说明本模型的预报场能捕捉与观测场一致的季节变化特征。然而, HYCOM 后置预报场的预报能力相对较弱, 特别是在赤道断面上的负值区域。这也进一步表明本模型对印度洋SSS的时空变化特征具有较好的预报优势。

图8 观测与预测SSS 之间的RMSE 及相关系数(印度洋区域)Fig. 8 RMSE and correlation coefficients between the observed and predicted SSS in the Indian Ocean

图9 印度洋区域赤道断面提前1~11 个月的SSS 观测(左)、马尔可夫模型预报结果(中)和HYCOM 后置预报结果(右)Fig. 9 SSS observations (left),Markov modelforecast results (center) and HYCOM hindcast results (right)for 1-11months earlier, onthe equatorial section of the Indian
4 结论与展望
本研究建立了一个MEOF 与线性马尔可夫相结合的模型来预测印度洋区域SSS 的变化。采用交叉验证和“实时”预测的方式评估了该模型的预测能力。基于 13 年逐月样本的统计模型, 使用印度洋的SSSA、SSTA 和SSHA, 保留前5 个模态, 对印度洋海表盐度进行预报, 结果表明该模型具有较好的性能, 大致可提前9 个月进行较好的预报。进一步考虑遥相关作用, 向该模型中添加南太平洋的SSHA, SSTA及IOD 系数, 预报效率平均提高10%(相关系数)。
本文采用的预报方法, 计算便捷且开发成本低,为变量的预测提供了一个很好的选择。但是, 在本文模型中, 加入蒸发量、降水量和海表面风场等物理量并不能给印度洋SSS 带来更好的预报效果, 目前尚不清楚原因, 需要进一步探究。未来我们将考虑更多的变量来拓展本文的工作, 并进一步推广至全球海洋SSS 的预测。

