基于生态灰色模糊风险分析水资源开发方案
刘 斌
(河北省沧州水文勘测研究中心,河北 沧州 061000)
水利工程具有消除水害,可开发利用水资源,保护人民财产安全作用,因此在经济社会发展过程中具有重要意义,在水资源利用和水资源建设中价值更明显,能够促进经济社会实现可持续性发展[1-2],但过度使用仍然会对环境产生一定不利影响[3]。目前,在一般环境影响评价报告中,仅定性描述了兴建水利工程对地球生态环境的影响,这导致人们对生态环境影响缺乏整体评价,只注重经济利益,不充分考虑建设工程带来的负面影响,这将对地球生态系统带来不可逆转的问题。如张丹[4]学者应用模糊灰关联故障树模型评估了水利水电工程的社会稳定风险;江新[5]等学者应用灰色模糊综合评价方法评估水利工程项目群供应链风险等级。因此,在水利工程环境影响评价报告中,应在综合考虑社会、经济和环境效益的基础上,核算兴建水利工程的生态环境价值,分析建设工程的可行性。为解决以上矛盾,本文在综合考虑水利工程效益、生态修复成本和生态风险的基础上,提出可以优化水利工程开发规模的模型。
1 建立考虑生态风险的优化模型
1.1 确定主要生态风险因子
影响水利工程生态环境的因素有很多,主要来自建设水利工程的施工阶段、运维阶段和拆除阶段,其主要风险因素如图1所示。

图1 水利工程生态风险因素

1.2 确定主要生态风险成因
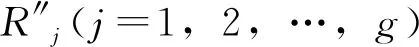
1.3 总生态风险变化预测
假设已经确定了n个开发规模的模糊风险值,则可以运用灰色理论预测模型,该模型为随水位增长的模糊风险值GM(1,1)模型。
1.4 考虑生态风险的优化模型
(1)假设n个开发方案通过不同的正常蓄水位(H=[h1h2…hn])进行比较,以反映开发规模的差异。第一步,计算每个开发方案能够产生的效益和需要的生态修复成本,则能够得到效益向量、工程成本向量和生态修复成本向量这三个向量,其中:效益向量B=[b1b2…bn]、工程成本向量C=[c1c2…cn]和生态修复成本向量D=[d1d2…dn]。
(2)根据上述计算方法,算出每个方案的系统总风险值,然后可以得到一个模糊风险向量R=[r1r2…rn]。
(3)利用回归拟合,找出效益作为正常蓄水位的函数,以EB(h)表示;工程成本作为正常蓄水位的函数,以C(h)表示;生态修复成本与模糊风险值也作为正常蓄水位的函数,分别以D(h)、R(h)表示。
(4)将上一步得到的四个函数组合在一起,可以得到新的单目标函数和多目标函数,见式(1)~式(3):
F1(h)=EB(h)-C(h)
(1)
F2(h)=EB(h)-C(h)-D(h)
(2)
(3)
(5)建立优化模型
目标函数为Fi(h),约束条件如式(4):
C(h)-EB(h)<0
C(h)+D(h)-EB(h)<0
(4)
-R(h)<0
hmin (6)运用最优化理论计算出前三个函数的极值,与极值对应的正常蓄水位表示最优开发规模。通过比较单目标和多目标开发规模的最优正常蓄水位,从而选择出最优正常蓄水位。 本文以某水利枢纽的相关数据为基础进行分析,可知其正常蓄水位可选择在223~233 m之间,因此设置6个正常蓄水位来代表该范围内不同的开发规模,主要表示为H=[h1h2…h6]=[223 225 227 229 231 233]。 计算生态系统总风险的模糊矩阵时,应遵循的步骤:首先建立评价对象因子集和评价集、以及不同开发规模下风险因素的模糊矩阵;然后根据模糊矩阵和风险因素的权重,利用模糊变换算法求出模糊矩阵中的风险因素;最后根据模糊逻辑并通过模糊变换算法,算出不同开发规模下生态系统的总风险模糊矩阵和风险因子权重。 根据生态系统总风险的模糊矩阵及对应权重,利用模糊变换算法得出生态系统总风险的模糊综合评价矩阵。 结合以上数据,算出不同开发规模下生态系统总风险的模糊评分,见表1。 由表1中数据可知,总风险模糊评分R与存储水位呈正比变化。表1中还显示了风险增量ΔR的变化:当水位小于229 m时,风险增量率与存储水位呈反比变化;当水位大于229 m时,风险增量率与存储水位呈正比变化。整体而言,风险增长速度在加快。 表1 不同开发规模下的总风险评分值 通过最小二乘法拟合出生态总风险因子与蓄水位(R~h)的关系曲线,见式(5): R=0.0003h2-0.1219h+13.88831 (5) 同上,通过最小二乘法拟合出工程施工阶段存在的风险因子与蓄水位(R1~h)间的关系式(6): R1=0.0004h2-0.1719h+19.1451 (6) 拟合得出工程运维阶段存在的风险因子与蓄水位(R2~h)间的关系式(7): R2=0.0002h2-0.0705h+8.3238 (7) 拟合得出工程运行结束之后拆除阶段存在的风险因子与蓄水位(R3~h)间的关系式(8): R3=0.0004h2-0.1740h+19.7459 (8) 根据最小二乘法拟合得出的蓄水位与总生态风险关系式、施工阶段关系式、运维阶段的关系式以及拆除阶段的关系式,能够得出固定范围内不同开发规模的生态总风险,以及该工程项目在其使用周期内特定范围中不同开发规模下的风险值。 通过模糊评价算法和模糊评分法,能够确定出不同开发规模下生态风险因子的模糊评分,如表2所示。 根据模糊评价算法和模糊评分法,可以确定不同开发规模下模糊评分的各种风险成因。通过对本项目全生命周期的生态风险分析,包括建设阶段、运维阶段和最终拆除阶段,可以得出以下结论:工程在建设阶段,最不利的风险因素是不可再生资源的消耗;在运维阶段,最不利的风险因素是破坏原始生物的栖息地;在运行结束后的拆除阶段,最不利的风险因素是环境生态服务功能的下降。因此,在执行某个建设方案的过程中,在工程建设阶段应该尽量减少消耗有限的天然燃料和生长速度较慢的再生材料,应提倡开发利用快速天然可再生的材料,实现保护生态环境的目的。在工程运维阶段,应尽量保护原有生物的栖息地,避免河流形式的均质化和间断化,不破坏生物环境,提倡生态水利。在最后拆除阶段,不仅要看到供水、灌溉、发电等水利工程给人类社会带来的直接效益,也要更加关注水利工程改变河流自然状态后,对环境生态系统、动植物多样性的负面影响。 表2 不同开发规模下生态风险因子的模糊评分 通过模糊综合评分计算方法,先计算出总生态风险值Ry i(i=1,2,…,m)。然后,建立水位hi(i=1,2,…,m)与总生态风险值Ry i(i=1,2,…,m)之间的关系来预测风险。Ry i是随水位上升而变化的一种已知信息,但仍存在一部分未知信息,即这种动态趋势的实质特征是灰色的。因此,需要通过灰色系统微分方程的建模机理和方法建立GM(1,1)模型。 本文建立的灰色预测模型,如式(9): R=0.066 103 7e0.008 868 54h (9) 根据上述模型,算出不同开发规模下的生态风险值,如表3所示。 表3 不同开发规模下的生态风险值 通过全面核算兴建水利工程对人类社会经济和当地生态环境的影响,可知水利工程对人类社会经济和当地生态环境的影响包括以下两部分:一是项目能够产生的效益EB和自身需要的成本C;二是水利工程对当地生态环境造成的价值损失D。利用水利工程经济分析方法,算出不同开发规模下生态环境的效益、成本和损失,如表4所示。 表4 不同开发规模下的工程效益、成本和损失 通过回归分析理论拟合计算出正常蓄水位h与工程效益EB(h)的函数如式(10): EB(h)=0.010 034h3-7.0229h2+ 1638.5h-127 300 (10) 拟合得出正常蓄水位h与工程成本C(h)的函数如式(11): C(h)=0.002 372 4h3-1.5972h2+ 358.62h-26 807 (11) 得出正常蓄水位h与生态修复成本D(h)的函数如式(12): D(h)=0.0137h2-6.0241h+685.2696 (12) 不同开发规模下不考虑生态风险的优化模型见式(13): F1(h)=0.007 662h3-5.4531h2+ 1279.9h-100 493 (13) 不同工程开发规模下考虑生态修复成本的优化模型见式(14): F2(h)=0.007 662h3-5.4394h2+ 1285.9h-101 178 (14) 不同工程开发规模下考虑生态风险的优化模型见式(15): F3(h)= (15) 以上三种不同模型的优化问题都是约束非线性规划问题,可采用复形法求解,结果如下: 当h=229.1 m时,F1(h)获得最大值,则说明在考虑工程效益和工程成本的情况下,水库最优正常蓄水位为229.1 m。 当h=228.3 m时,F2(h)获得最大值。则说明在考虑工程效益、工程成本和生态修复成本的情况下,水库最优正常蓄水位为228.3 m。 当h=227.4 m时,F3(h)获得最大值。则说明在考虑工程效益、工程成本、生态修复成本和生态风险的情况下,水库最优正常蓄水位为227.4 m。 通过本文计算分析不同开发规模下优化模型的结果,可从中得到以下结论: (1)仅考虑工程效益和工程成本的单目标优化模型中,水库最优正常蓄水位为229.1 m,而实际正常蓄水位为228.0 m,说明实际值明显小于计算结果,与实际不符。 (2)综合考虑工程效益、工程成本和生态修复成本的优化模型中,水库最优正常蓄水位为228.3 m,而实际正常蓄水位为228.0 m,说明实际值略小于计算结果,与实际存在一定差别。 (3)考虑工程效益、工程成本、生态修复成本以及生态风险的多目标优化模型中,水库最优正常蓄水位为227.4 m,实际正常蓄水位也是228.0 m,说明实际值略大于计算结果,虽存在一定出入,但结合计算结果分析,该模型更符合实际情况。 (4)只考虑工程效益和工程成本的情况下,当水库最优正常蓄水位在229.1 m以下时,水位与收益呈正比变化;当水位超过最优正常蓄水位时,水位与收益呈反比变化、与工程成本呈正比变化。通过多目标分析可得,生态修复的总成本和生态风险均随着水位增加而增加,因此,其发展规模相比单目标较小。2 生态系统总风险的计算
2.1 建立不同开发规模
2.2 生态系统总风险的模糊矩阵
2.3 生态系统总风险的模糊综合评价矩阵
2.4 生态系统总风险的模糊评分

3 不同阶段生态风险因子与蓄水位间的变化关系
3.1 确定主要生态风险成因
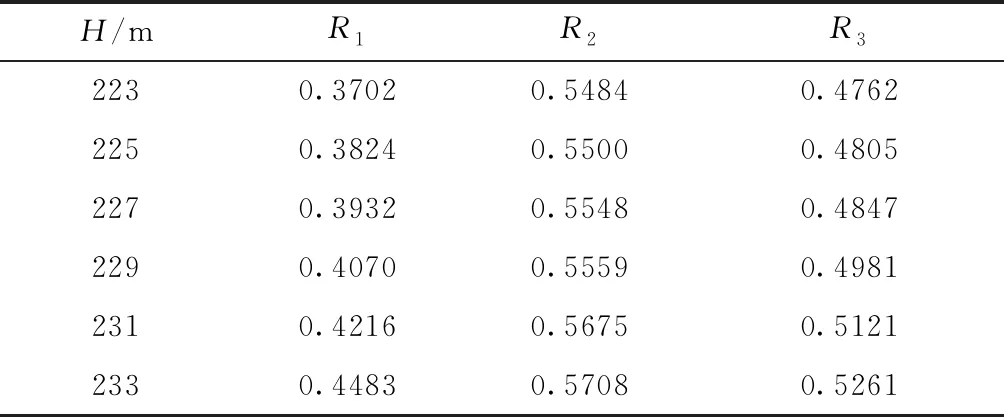
3.2 生态总风险的灰色预测

3.3 不同建设规模效益与成本的计算

3.4 优化模型
4 结 论

