常州市国控站PM2.5监测的代表范围研究

王振，宋京京，余益军，杨卫芬，叶香，李璐

(1.江苏省常州环境监测中心，江苏 常州 213001；2.北京市气象信息中心，北京 100089)

2013年《大气污染防治十条措施》(“大气十条”)颁布以来，我国在全国范围内开展细颗粒物(PM2.5)地面监测。相关研究表明，PM2.5污染呈明显的区域性分布特征[1-3]，区域内气候、社会经济、人口、产业结构与工业布局等要素对PM2.5质量浓度起决定影响作用[4-8]。具体站点的PM2.5监测除受气候等影响外，还受周边一定范围内的源排放、能源结构等因素影响[9]。随着环境管控措施不断加强以及站点周边环境发生变化，如人口聚集变动和建成区面积增大等，造成站点周边大气环境特征改变，PM2.5监测所能代表的范围也随之发生动态变化。

为研究常州市国家大气自动监测站(以下简称“国控站”)PM2.5监测的代表范围，需要稠密的PM2.5空间分布数据。由于地面站点较少且分布不均，缺乏高空间分辨率的PM2.5监测数据进行相关研究[8,10-11]。卫星监测能够大范围、长时间地对气溶胶光学厚度(AOD)进行监测，而且已有许多研究采用AOD数据估算PM2.5质量浓度[12-15]，该方法能够有效弥补地面站点监测空间与时间上的不足。

现以最优分割等统计方法，结合卫星遥测AOD数据估算的PM2.5质量浓度，探索常州市国控站PM2.5所代表的范围和该范围随时间的变化。

1 研究方法

1.1 数据来源

1.1.1 国控站监测数据

国控站监测数据来自2013—2019年常州市区6个国控站PM2.5日均浓度，国控站与市区重要水域分布示意见图1。除“安家”外，其他5个国控站均集中分布在主城区，“行政中心”和“市监测站”直线距离最短(约 6.3 km)；“安家”与其他国控站的直线距离均在12 km以上，与“武进监测站”直线距离最远(约23.3 km)。各点位中PM2.5监测方法均为β射线法，数据统计有效性依据《环境空气质量监测点位布设技术规范》(HJ 664—2013)[16]判定，若日数据无效则排除分析。

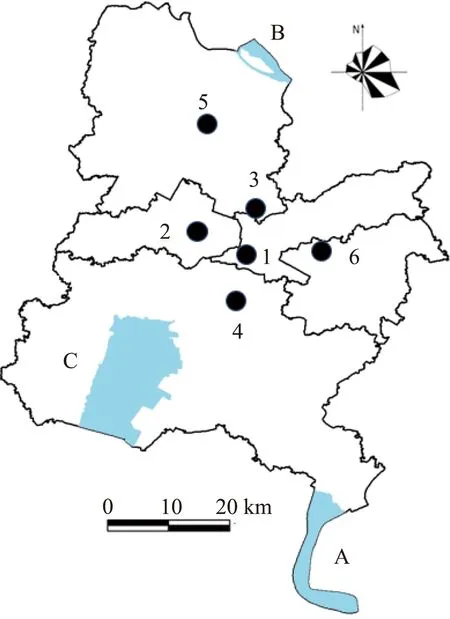
注：1—市监测站；2—钟楼；3—行政中心；4—武进监测站；5—安家；6—经开区；A—竺山湖；B—长江常州段；C—滆湖。

1.1.2 卫星监测数据

估算PM2.5浓度的AOD数据来源于Terra和Aqua卫星多角度大气校正算法(MAIAC) AOD产品(MCD19A2，https://ladsweb.modaps.eosdis.nasa.gov)，空间分辨率为1 km。DT和DB产品主要指利用深蓝算法(DB)和暗目标算法(DT)反演得到的550 nm AOD产品[17-19]，DB算法主要是为了解决DT算法在城市、沙漠等高地表反射率情况下失效的问题[18-19]。有研究表明，MAIAC AOD在中国表现性能良好，且产品准确度和时空完整性也优于DT、DB产品[20-24]。MAIAC AOD反演与地面AOD测量验证中[25]，二者结果高度相关，超过68%的AERONET气溶胶数据站点的相关系数>0.8；在热带雨林气候和热带疏林气候地区，MAIAC AOD反演的精度较高[25]。MERRA-2(https://disc.sci.gsfc.nasa.gov/)是NASA开发的长时间序列的再分析数据集，由戈达德地球观测系统第5版(GEOS-5)驱动，为海洋、陆地和大气成分的研究提供长时间序列资料，其空间分辨率为 0.625°×0.5°。MERRA-2可以较好地复现PM2.5的变化趋势[26]，其包括基本气象变量(温度、相对湿度、风速等)和5种地表气溶胶数据(灰尘、海盐、黑炭、有机碳和硫酸盐)。本研究采用MEERA-2作为辅助数据，反演范围为常州市区。

1.2 数据匹配与估算方法

估算PM2.5浓度所采用的变量为1 km空间分辨率的MAIAC AOD、格点经纬度、日期、MERRA-2再分析数据。为确保时空匹配，首先将MAIAC AOD利用线性插值方法，格点化到0.01°(即1 km×1 km)的空间分辨率，同时对MERRA-2资料也使用相同手段格点化，匹配相应时间和空间格点化后的MAIAC AOD和MEERA-2等资料与6个站点的PM2.5监测浓度数据合并统一，建立对常州普适的AOD至PM2.5的对应关系，然后以该对应关系推广到常州市全域各格点进行估算反演。

以随机森林(RF)方法估算PM2.5浓度，采用相关系数、均方根误差等统计指标为评价依据。RF是以决策树分类器为基本单元的集成算法[27-28]，通过自助法重采样技术，从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练样本集合，重复抽取T次，形成T个独立数据集。以每个采样集训练1颗基决策树，T个采样集训练成为T个基决策树，由此组成随机森林。决策树在机器学习中是一个预测模型，代表了对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，每个分叉路径则代表某个可能的属性值，每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。本研究应用决策树CART(Classification and Regression Tree)算法对常州市PM2.5浓度进行估算。

1.3 相关统计计算

1.3.1 PM2.5空间异质性分析

环境空气中PM2.5浓度在空间中的分布受到诸多因素的影响，一般而言，PM2.5浓度在空间分布上具有一定的相关性，且距离越近相关性越强。变异函数[29-30]可作为空间表征参数对PM2.5的空间自相关性进行研究，可以较好地揭示区域PM2.5不同空间方向浓度差异的统计分布规律。其计算公式见式(1)。

(1)

式中：γ(h)——变异函数；Z(xi)、Z(xi+h)——在xi和xi+h空间位置处的PM2.5反演值；N(h)——样本点数。变异函数能够同时描述区域化变量的随机性和结构性，从而在数学上对区域化变量的相关性进行严格分析，因此是PM2.5空间变异分析和结构分析的有效工具。

1.3.2 最优分割

为分析探讨站点PM2.5监测代表的范围，需要探讨不同范围下的PM2.5估算浓度与实测浓度的相似性，若某半径下PM2.5的估算浓度与站点的实测浓度相似度达到最高，则此半径所代表的范围为该站点PM2.5监测的代表范围。站点监测的PM2.5浓度与不同范围(半径由小到大)的PM2.5估算浓度构成有序序列，在有序序列上寻找某半径下估算浓度与实测浓度相似度达到最大的最优分割点，使得该半径范围为站点监测所能达到的最大范围。

有序序列最优分割点的确定通常采用有序聚类方法，该方法也称最优分割，具体的算法参见文献[31]。为简化分析，假设仅有1个最优分割点(即进行二分)，使得一定范围内的估算浓度与实测浓度相似度达到最大，从而确定该站点PM2.5监测的代表范围。最优分割点确定的依据选用离差平方和，如果分割点内所有样本的离差平方和最小，分割点外所有样本的离差平方和最大，则表明该分割是合理的。为统一比较常州市6个国控站PM2.5监测的代表范围，各个站点离差平方和采用最小值-最大值标准化进行线性变换，使离差平方和投影到[0,1]区间内，从而进行统一比较。由于本研究使用的AOD空间分辨率为1 km，因此估算站点PM2.5监测的代表范围时所采用的半径步长亦为1 km。

1.3.3 热点分析

利用热点分析探测出PM2.5具体区域的空间分布属于高值集聚还是低值集聚，讨论常州市区PM2.5热点、冷点和随机区域的集中位置。热点分析采用Getis-OrdGi*冷热点分析以区分PM2.5的高值或低值的局域空间集聚，以及哪个区域单元的PM2.5对于全局空间自相关的贡献更大[32]。Getis-OrdGi*可以用来探测PM2.5在局部水平的空间集聚程度，衡量局部集聚并给出区域内不同区块位置的高值簇(热点区域)和低值簇(冷点区域)，计算公式见式(2)和式(3)。

(2)

(3)

式中：Gi*——检验值，显著的正Gi*值表示在该区域周围，PM2.5高观测值趋于空间集聚，而显著的负Gi*值表示在该区域周围，PM2.5低观测值趋于集聚；n——常州市区PM2.5空间格点数目；xj——相应格点j的PM2.5值；ωij——空间权重系数，具体定义由参考文献[32-33]中的二进制空间权重确定；x——PM2.5浓度平均值。

2 结果与讨论

2.1 PM2.5估算统计验证

以常州市6个国控站各自所在网格(1 km×1 km)的AOD数据结合MERRA-2数据，采用RF方法估算PM2.5浓度。排除实测与估算的缺失值，2013—2019年6个站点共得到7 261个日有效数据。结果表明，6个国控站逐日PM2.5实测质量浓度与估算质量浓度的相关系数为0.958，均方差为7.5，估算效果总体优异(图2)。

图2 PM2.5估算与实测质量浓度的线性关系

2.2 PM2.5浓度空间分布

以估算的各网格点PM2.5日均质量浓度的平均值代表常州市区PM2.5日均质量浓度，2013—2019年常州市区PM2.5估算质量浓度与实测质量浓度的空间分布见图3(a)(b)。由图3可见，PM2.5质量浓度为35～70 μg/m3。以“经开区”为代表的东部区域浓度相对较高，市区西南部浓度相对较低；从整体上看，由东北向西南浓度逐步降低。2013—2019年，以6个国控站为代表的常州市区PM2.5实测质量浓度为 56.2 μg/m3，而对应时间段常州市所有格点的PM2.5估算质量浓度为57.6 μg/m3，比实测质量浓度偏高1.4 μg/m3，偏高幅度为2.5%。综上，6个国控站的PM2.5实测质量浓度能够代表常州市区PM2.5的总体水平。

从图3(a)可见，常州市区PM2.5浓度空间分布存在集聚现象，偏东部区域浓度相对较高。各个国控站所在格点的PM2.5浓度与一定范围区域内的浓度相近，但超过一定范围后浓度出现明显变化界限，如“经开区”与“市监测站”站点之间产生浓度变化，存在明显的分界线。综上，尽管6个国控站能够代表常州市区PM2.5的总体水平，但不能详细表达PM2.5的空间分布情况，更不能明确表达各个国控站PM2.5实测浓度的代表范围。

Getis-OrdGi*能够指示出区域内高/低值簇不同的区块位置，常州市区PM2.5估算质量浓度热点区主要分布在偏东区域，冷点区主要集中在西南方位和东南角；其他的区域基本处于无明显冷热点的随机区域(图4)。通过冷热点分析，常州市区东部为主要污染区域，但该区域仅有一个“经开区”国控站，需要加强该区域的监测覆盖率。

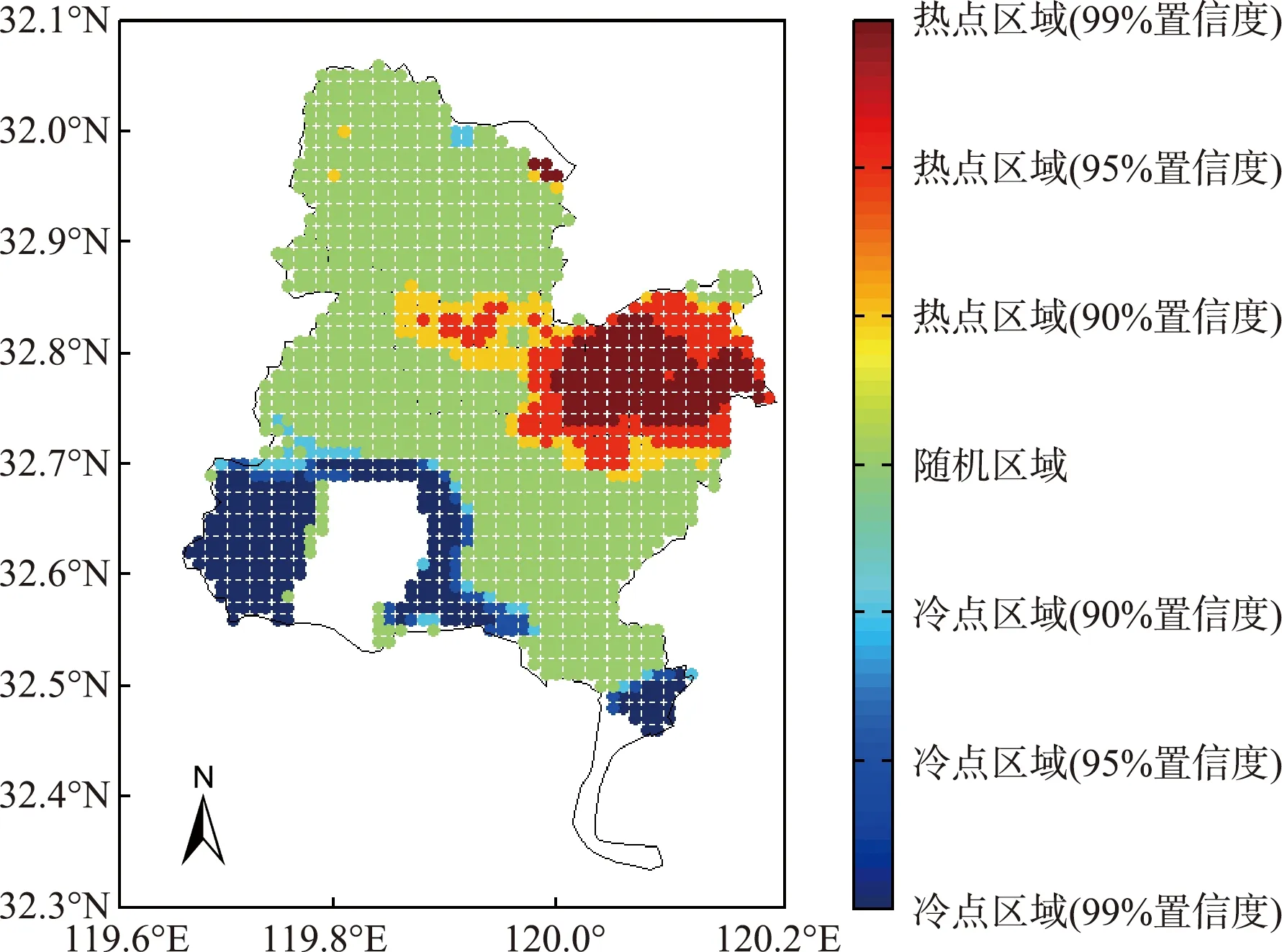
图4 PM2.5热点分析

2.3 PM2.5空间异质性研究

为研究常州市区PM2.5浓度空间相关性范围的大小，对2013—2019年的PM2.5估算浓度进行空间异质性分析，即对各个格点的PM2.5均值浓度进行变异函数计算。PM2.5空间自相关统计见图5。

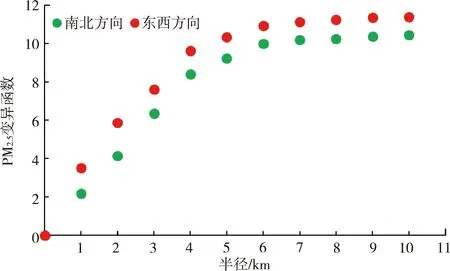
图5 PM2.5空间自相关统计

由图5可见，在一定范围内，随着空间距离的增加，PM2.5南北方向和东西方向的变异函数均逐步增加，但当距离增至约5 km后，变异函数上升幅度明显减缓，而后缓慢增加趋于水平。半径为0～5 km对应的变异函数上升迅速，表明常州市区PM2.5浓度随着观测点之间的距离增加，相关性逐渐减小，PM2.5空间分布的异质性逐渐增大；而半径>5 km，变异函数缓慢上升，表明PM2.5观测点之间的异质性接近局部最大。半径在5 km范围内各个位置的PM2.5浓度存在一定的空间相关性；但当半径>5 km后格点间PM2.5浓度空间相关性变小。一定区域内的PM2.5浓度差异较小可能是由于污染源排放辐射范围、局地微气象和地形等因素引起的，超过一定范围后环境差异逐渐增大，从而导致PM2.5浓度差异也增加。总体上看，常州市任一格点的PM2.5浓度与较近范围内的格点浓度具有较好的相关性，超过5 km范围后污染物浓度空间差异增大。

2.4 国控站PM2.5监测的代表范围

采用最优分割中的二分法，对各个国控站2019年PM2.5实测浓度与不同半径下估算浓度进行统计分析以寻找最优分割点。最优分割的标准化离差平方和见图6。

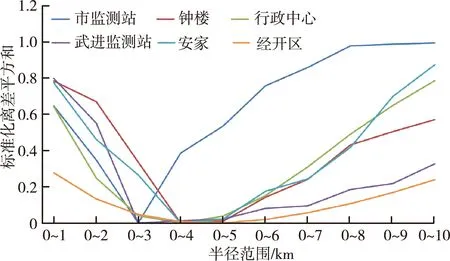
图6 最优分割的标准化离差平方和

由图6可见，“经开区”站点在半径5 km内标准化离差平方和最小，5 km范围外的标准化离差平方和开始增大，表明在5 km范围内，PM2.5估算浓度与实测浓度的差异性最小，5 km范围外差异性开始变大，因此“经开区”站点PM2.5监测的代表范围半径为5 km。其他站点类似，“钟楼”“行政中心”和“安家”站点PM2.5监测的代表范围半径为 4 km，“市监测站”和“武进监测站”站点PM2.5监测的代表范围半径为3 km。有序序列的最优分割分析表明，常州市各个国控站PM2.5监测均存在代表范围，总体在3～5 km内，与《HJ 664—2013》中500～4 000 m的范围基本一致。“经开区”站点的代表范围最大，可能原因是该站点所在区域的PM2.5浓度整体较高，当半径增大后，估算浓度“由高至低”导致该区域内PM2.5均值浓度变化相对较小，与站点监测浓度差异性变化不大。“市监测站”和“武进监测站”处于PM2.5整体相对较低的区域，当半径增大后，估算浓度“由低到高”导致该区域内PM2.5均值浓度变化相对较大，与站点监测浓度差异性变化迅速显现。

常州市国控站PM2.5监测的代表范围逐年变化情况见图7。由图7可见，总体而言，各个站点PM2.5监测的代表范围呈增加的趋势，侧面表明常州市“大气十条”和《打赢蓝天保卫战三年行动计划》实施以来，环境管控措施有力，PM2.5浓度空间分布整体趋向均匀。

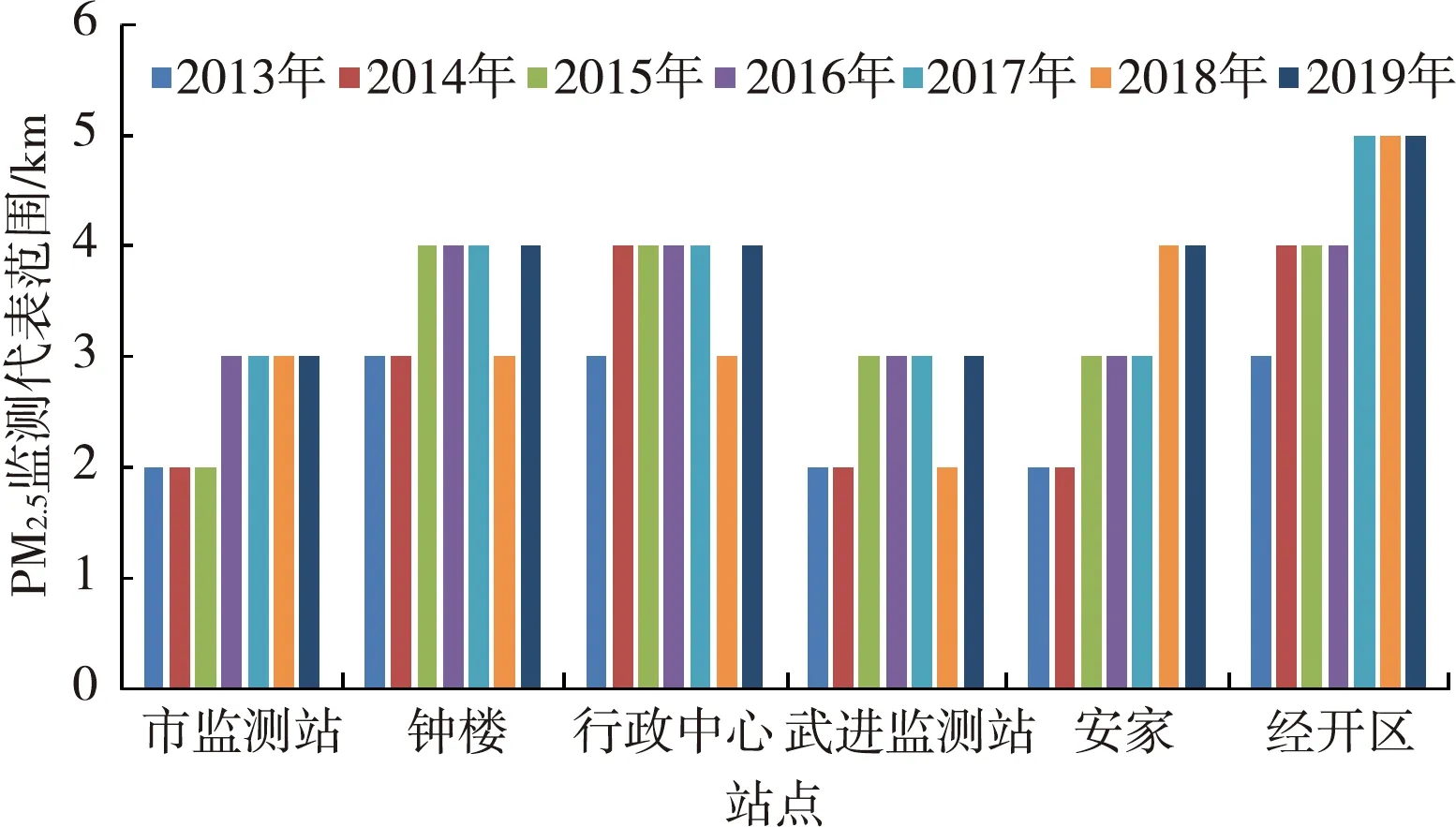
图7 国控站PM2.5监测的代表范围逐年变化

3 结论

(1)采用MAIAC AOD结合随机森林方法对2013—2019年常州市PM2.5浓度进行估算，估算质量浓度为57.6 μg/m3，比实测质量浓度偏高2.5%，效果较好，能够弥补常州市PM2.5地面站点相对较少和分布不均匀的缺点。

(2)对常州市反演的PM2.5浓度进行异质性分析，各网格PM2.5反演浓度在5 km范围内存在较好的空间相关性；当距离超过该范围后，空间差异性导致PM2.5出现异质现象。

(3)通过最优分割得出常州市6个国控站PM2.5监测的代表浓度范围。其中“经开区”站点代表范围最大，为5 km；“市监测站”和“武进监测站”站点代表范围相对较小，为3 km。

(4)2013—2019年，各个国控站PM2.5监测的代表范围总体呈增加趋势。