人工冻结黏土经验模型参数确定及蠕变规律验证

姚兆明 李 南 郭梦圆

(安徽理工大学土木建筑学院,安徽 淮南 232001)

人工冻结法为我国矿山立井建设提供了重要的技术支撑,解决了包括快速钻爆千米级深竖井及深厚冲积层不稳定性等系列难题[1]。因此,人工冻土领域的研究愈来愈受到关注,其中许多工程问题与人工冻土蠕变特性有着密切关联,为确保工程安全,建立能够描述蠕变特性的本构模型及掌握识别模型参数的方法尤为重要。

近年来,国内外学者开展了大量蠕变试验对岩土材料蠕变各阶段变形随时间的发展规律进行了研究,建立了适用于不同岩土材质的蠕变本构模型。CAO等[2]在不同应力水平下研究了岩石的黏弹塑特性,建立了一种元件模型并明确了模型参数求解方法;齐亚静等[3]在传统西原模型上串联非线性黏壶,同时建立了可以考虑岩石流变特性的改进西原模型,并利用试验数据对模型性能进行验证,进一步明确了参数确定方法。

此外,诸多学者开始关注低温环境下土体蠕变发展规律,开展冻土蠕变本构模型研究。YANG等[4]进行了冻结粉土蠕变试验,建立了适用于冻结黏土的蠕变模型;李鑫等[5]考虑环境温度和加载应力等影响因素引起人工冻土的强化与弱化,引入硬化与损伤两种因子并建立了适用于冻土的蠕变本构模型;杨岁桥等[6]进行大量考虑温度和荷载等因素影响的蠕变试验,结果表明:温度是影响冻土蠕变最重要的外在因素;刘萌心等[7]在融土蠕变模型基础上,引入温度变量并通过冻土K0加载试验得到模型相关参数,建立了能够考虑温度影响的一维冻土蠕变模型;罗飞等[8]在Nishihara模型基础上考虑应力水平对黏滞系数的影响,并引入损伤因子建立了冻结砂土蠕变模型;ZHAO等[9]在不同温度梯度和应力条件下进行了大量单轴蠕变试验,建立了能够考虑热梯度效应的元件模型;姚兆明等[10-11]引入S-M蠕变模型分析温度、含水率、加载应力等因素影响的冻土蠕变特性,通过对试验值取对数等方法计算了模型参数;陈军浩等[12]、HOU等[13]基于分数阶理论建立了冻土蠕变模型,并提出能够描述冻土蠕变特性的新方法;李祖勇等[14]、姚亚锋等[15]、LI等[16]、王兴开等[17]分别基于相关优化算法对蠕变模型参数进行辨识并通过试验值验证了模型性能;朱纪斐等[18]基于遗传算法对建立的经验模型进行参数优化,结果表明:该模型能够计算人工冻土蠕变各阶段的应变。以上蠕变模型参数基本是通过最小二乘法拟合得出,参数只有数学意义而不具备物理意义。

本研究以原状黏土为试验对象,在不同冻结温度下进行单轴压缩强度测试及不同应力水平的蠕变试验,通过建立经验蠕变模型,对不同冻结温度和加载等级条件下的应变和时间取对数,并将其代入对应方程组联立求解确定蠕变模型参数。将识别参数后的模型计算值与室内试验值进行对比,发现两者吻合度较高,反映出该模型参数确定方法的合理性及正确性,所求解的模型参数同时具备数学意义和相应的物理意义。

1 原状黏土冻结试验

1.1 原状黏土单轴抗压强度试验

试验在WDT-100型人工冻土多功能试验仪器中进行[19],该试验机能够即时采集试件产生的应力和应变。试验样品来源于某矿井深部地层原状黏土,煤矿井筒检查孔取样深度为92.06～97.65m,原状土包装见图1(a),共取了25筒。土样在运输过程中保持常温,在实验室中按设定温度进行冻结,冻结后的试件见图1(b)。试件含水量约22%,干重为17.2 kN/m3,根据标准加工为高度d=100 mm、直径ϕ=50mm的圆柱形试件。将加工后的试件分别置于-5、-8、-10、-15℃温度下养护不少于24 h,各温度下进行平行试验。由于土样在运输时出现破损现象,因此在个别温度下只做了2件试件的平行试验。图1(c)、图1(d)分别为按标准加工的试件及试验破坏后的试件。以3件试件内部最大应力的平均值作为试件最终单轴抗压强度,试验结果见表1。

图1 试件制备及破坏前后对比Fig.1 Preparation of specimens and comparison before and after failure

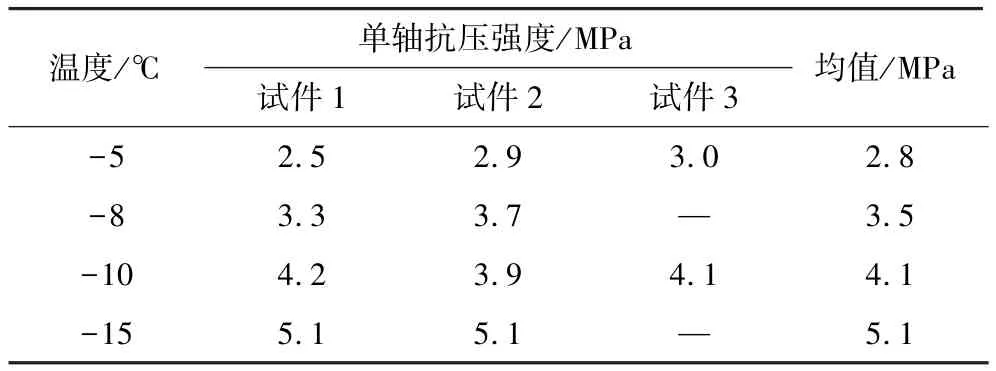
表1 各负温下的试件单轴抗压强度Table 1 Uniaxial compressive strength of specimens at different negative temperatures

对冻结抗压强度与温度进行拟合,得到人工冻结黏土的抗压强度与温度在一定条件下呈线性关系,如图2所示。

图2 温度与单轴抗压强度关系曲线Fig.2 Relation curves between temperature and uniaxial compressive strength

结合图2可知:温度与冻结抗压强度两者之间满足如下关系:

式中,σs为单轴抗压强度,MPa;T为冻结温度,℃。

由式(1)可知,冻结温度越低,单轴抗压强度越大,温度由-5℃降至-8℃时,冻结抗压强度提升达25%,且在试验温度范围内,温度每降低1℃,人工冻结黏土的单轴抗压强度增加约0.23 MPa。

1.2 原状黏土单轴蠕变试验

将加工后的试件分别置于-5、-8、-10、-15℃不同冻结温度下进行单轴分级加载蠕变测试,加载等级为0.3σs和0.5σs;将试件加载到0.3σs应力水平且蠕变曲线稳定时,便将应力水平提高到0.5σs,达到设置的试验结束条件时停止试验。试件在各温度下的加载情况见表2,此次试验依照相关标准进行。

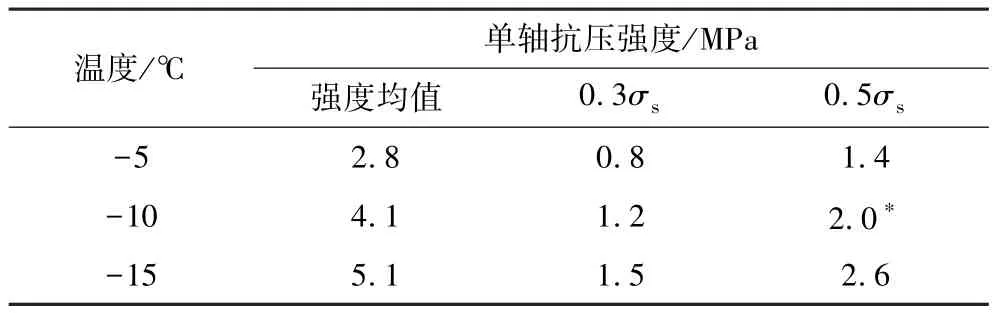
表2 各负温下试件分级加载的荷载值Table 2 Graded load values of specimens under each negative temperature

单轴蠕变试验采用分级加载方式,试件在不同加载等级下的应变—时间曲线如图3所示。由图3可知:试件变形速率逐渐减小,轴向变形趋于稳定。试件由初始阶段达到稳定蠕变阶段经历的时间大致相同,如在不同冻结温度下加载等级为0.3σs时,大约为1.8 h。当加载应力增大时,试验由初始蠕变至常应变蠕变阶段的时间也相应缩短。在同一冻结温度条件下,由一级应力水平加载至二级应力水平时,试件应变明显增大,如在-5℃冻结温度下,加载系数分别为0.3σs和0.5σs两级应力水平时达到稳定蠕变阶段的应变值分别为0.77%和2.31%,应变值大幅提升。可见,试件在冻结状态下,应力水平对稳定蠕变值有显著影响。

图3 各负温下的冻结试件蠕变曲线Fig.3 Creep curves of frozen specimens at each negative temperature

2 人工冻土蠕变数学模型建立及模型参数确定

由文献[20]可知,以幂函数的组合形式能够描述人工冻土蠕变特性,据此建立的经验模型为

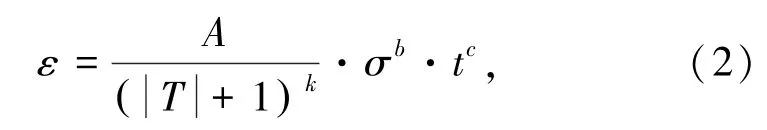
式中,ε为试件应变,%;t为试验时间,h;A为模型参数;k为反映温度影响的模型参数;b为反映加载应力影响的模型参数;c为反映时间影响的模型参数。

令:

则参数a是由试验冻结温度确定的常数,进而得出由试验温度与加载应力等因素影响的经验模型:

分别将各温度、加载等级下的应变与时间取对数,发现在同一加载等级、不同冻结温度条件下的应变与时间取对数时具有线性关系。因此将各温度下、不同加载系数的试验值分别代入建立的模型中,联立方程组对模型参数进行求解。T=-5、-8、-10、-15℃时的lgε—lgt曲线如图4所示。由图4可知:通过对各温度下不同加载系数的应变及对应的时间取对数,发现同一加载系数下不同冻结温度的应变与时间呈线性关系,并且在不同加载系数、不同冻结温度下两者也呈线性关系。

图4 各负温下不同应力水平的应变与时间对数曲线Fig.4 Logarithmic curves of strain and time at different stress levels and negative temperatures

对式(4)两边同时取对数得到式(5),且不同加载系数下各冻结温度的应变与时间的线性拟合关系如图4所示。

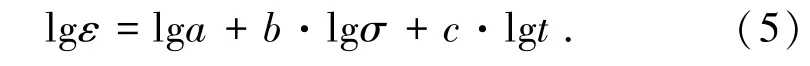
冻结温度在-5℃下,加载系数分别为0.3σs、0.5σs的线性表达式为

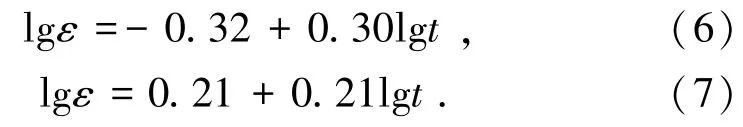
冻结温度在-8℃下,加载系数分别为0.3σs、0.5σs的线性表达式为

冻结温度在-10℃下,加载系数分别为0.3σs、0.5σs的线性表达式为

冻结温度在-15℃下,加载系数分别为0.3σs、0.5σs的线性表达式为

结合式(5)可知,图4中的lgε—lgt曲线斜率为模型参数c值,因此对式(6)至式(13)线性表达式的斜率取平均值,可得参数c=0.25。

对t=4 h时的ε值取对数,结果见表3。将其代入式(5),得到不同冻结温度下各加载等级的方程组,通过对其联立求解可得不同冻结温度下的参数a和b值。

表3 各负温下的应变对数值Table 3 Logarithmic values of strain values at different negative temperatures

冻结温度T=-5℃时,将σs=2.80和表3中对应的数据代入式(5)得:

联立式(14)、式(15)求解得:a=0.75,b=2.15。

同上,将T=-10、-15℃条件下对应的数据代入式(5),可联立求解各冻结温度下的参数a和b值,结果见表4。同时对参数b取平均值,得b=1.47。

表4 各负温下的参数a及b值Table 4 Values of parameters a and b at each negative temperature

由式(3)可知,对参数与冻结温度进行拟合,拟合相关度R2=0.99(图5),同时可以确定参数A和k值,可得:

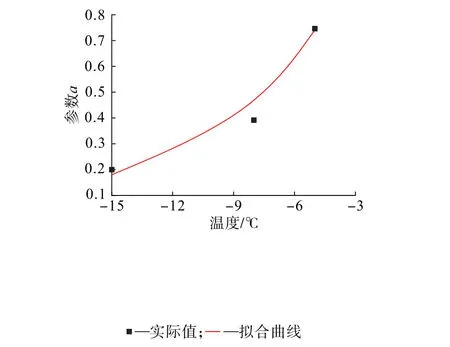
图5 参数a与冻结温度的关系曲线Fig.5 Relation curve between parameter a and freezing temperature

最终得到与冻结温度、加载应力有关的经验蠕变模型为

式中,η为加载等级。

通过所得经验蠕变模型计算人工冻结黏土在各负温下的应变值(图6),并计算了试验值与计算值的相关系数,结果见表5。

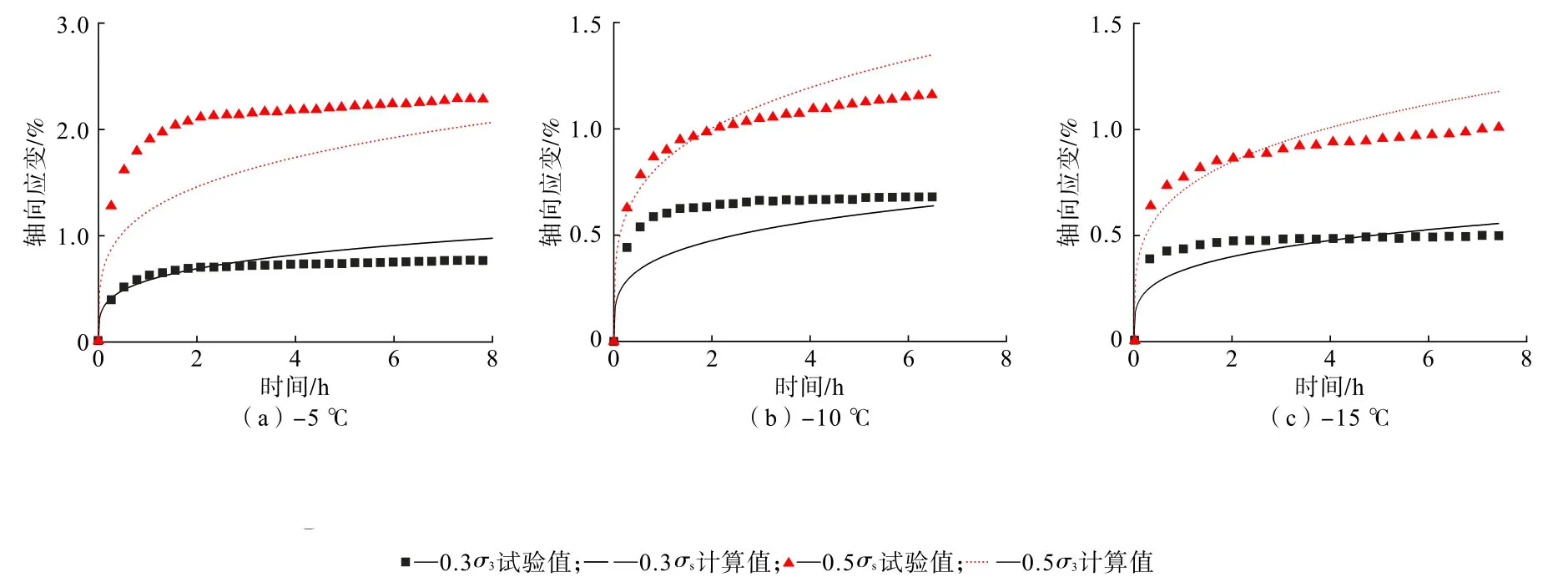
图6 模型预测值与试验值对比Fig.6 Comparison of the model predicted values and experimental values

表5 不同条件下试验值与计算值的相关系数Table 5 Correlation coefficients between test value and calculated value under different conditions

对比经验模型计算曲线与单轴蠕变试验曲线可知,所建立的经验模型能够较好地描述人工冻结黏土初始变形与稳定变形阶段。人工冻土单轴压缩蠕变试验同时受冻结温度、加载等级等因素影响,在不同的加载等级条件下,冻土蠕变规律与工作温度的关系较为复杂。当试件工作温度相同、加载等级增大时,人工冻土蠕变稳定阶段的应变显著增大,且温度的改变对冻土稳定蠕变阶段的变形影响较大。由图6应变—时间曲线可知,试件在单向压缩条件下表现出衰减型蠕变特征,即初始蠕变阶段和稳定蠕变阶段表现为非线性特征。

3 结 论

(1)对矿井深部地层黏土进行物理力学特性试验,分析了人工冻土蠕变特性受冻结温度与加载应力的影响规律,并在此基础上提出了蠕变模型参数求解方法,为冻结壁稳定性设计提供了一种新模型。

(2)一般性经验蠕变模型的参数是通过最小二乘法得出,导致模型参数无明确的物理意义。本研究建立的经验模型参数通过对试验值取对数代入相应方程组联立求解确定,模型参数同时具备了数学意义和物理意义。

(3)本研究建立的经验模型参数较少且易于确定,便于在冻结法施工中进行冻结壁稳定性计算。随着应力加载系数增大,土体内部将出现损伤。由于该模型未考虑土体损伤影响导致加载系数为0.5时,试验值与计算值出现较大偏差。因此在建模中进一步考虑损伤是后续研究方向。