批次受限的双目标并行机等量分批调度
朱颖颖,吴正佳,唐秋华+,孟荣华
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,湖北 武汉 430081;3.三峡大学 机械与动力学院,湖北 宜昌 443002)
1 问题的描述
多品种、小批量、交期短是现行客户订单的普遍特征,与此相反的是在其生产过程中,存在制造周期长、设备通用化等弊端,会降低车间生产效率、加大交货延迟风险。为此,企业常用措施是将一个订单或一批工件拆分为多个批次,多台机器并行加工,达到加快生产进度、缩短制造周期的目标。此类问题常称为并行机分批调度问题,由于各批次在不同机器上加工时可能存在时间重叠,部分文献也称其为并行机批量流调度问题[1]。
并行机分批调度是NP-难问题,与传统的并行机调度相比,其不同点是需要将一批具有一定数量的工件分为若干子批;相同点是需要将各子批分配到并行机上,再进行加工。与分批相反的批量调整策略是组批[2](Batching),它需要将不同工件整合成一个批次,故还需决策每个子批内不同工件的加工顺序。并行机分批策略通常包括等量分批和可变分批[3]两种,其中等量分批要求每个子批的批量相等,而可变分批与其相反。本文研究的是并行机等量分批调度问题(Parallel Machine Equally Lot-sizing and Scheduling Problem,PM-ELSP),不仅要制定分批策略,还需考虑子批在各台并行机上的排序和定时问题[4]。
诸多学者研究启发式或元启发式算法,来求解并行机分批调度问题。WANG等[5]针对太阳能电池制造,提出混合粒子群算法,解决具有多阶段的并行机分批调度问题,指出各子批的机器分配、批量确定和生产排序三者之间是彼此关联、互为条件的,需要联合优化。GÜNGÖR等[6]考虑到机器要么空闲、要么满负荷工作,没有中间状态,故以最小化工装夹具等装备安装和卸载次数为目标,设计启发式算法,求解并行机分批调度问题。EREMEEV等[7]以最大完工时间最小为目标,研究具有不相关并行机、工件可绝对均衡分批的并行机分批调度问题,且通过数学证明了该问题的NP-难特性。DE ARMAS等[8]提出一种数学规划和后处理排序启发式相结合的方法,解决以最大化总产量为目标的并行机分批调度问题。DANESHAMOOZ等[9]提出结合自适应的变邻域搜索算法,解决以最大完工时间最小的并行组装站分批调度问题。WANG等[10]提出融入交叉和变异算子的差分进化算法,求解以最大完工时间最小为目标的单目标并行机分批调度问题。WANG等[11]设计了一种基于规则的贪婪启发式算法,求解以最大完工时间最小为目标的单目标并行机分批调度问题。
综上可见,分批调度能缩短制造周期、减少生产提前期(如图1),故而被广泛应用。但是,当前并行机分批调度研究主要针对单目标优化问题,很少使用多目标优化,且目标主要是最大完工时间的最小化。针对分批过程中产生的若干子批,如何保证各子批工件能同时、准时进行交付,尚无文献进行研究。此外,上述研究中每批工件可划分的子批数目是定值,而实际工作中不同工件、不同批量,所划分的子批数量亦不相同。并且,在实际生产中,刀具成本高昂,可用刀具数目受限,对于工件划分的批次数目存在约束,上述研究均无考虑。

因此,本文以完工时间和交付时间偏差最大值的最小化为优化指标,在考虑刀具数量、切换时间等约束条件下,求解批次受限的多目标并行机分批调度问题。设计改进的多目标鲸鱼群算法(Multi-objective Whale Swarm Algorithm, MOWSA)实现工件分批、机器分配与子批排序3个子问题的联合求解。
2 批次受限的双目标并行机等量分批调度模型
随着柔性化能力的提升,在数控加工中心等加工设备上只需更换刀具,便可对不同工件进行加工。同时,由于刀具造价高、不易配套齐全,使得刀具数量有限,其数量小于加工设备的数量。因此,在生产调度时需要考虑刀具约束,保证每个工件能被合适的刀具加工。同时,考虑到一批工件需要同时、准时进行交付,工件分批数量应小于并行机数量;又因为刀具约束,工件批次数量更应小于刀具数量。由此,考虑刀具约束的并行机分批调度问题本质上就变成了批次受限的并行机分批调度问题。该问题可以描述为:假定某车间有M台并行机,需对N种工件进行加工,每种工件的批量已知,每批工件所能采用的刀具数亦已知,且刀具数小于并行机台数。
针对该问题,提出以下假设:①在一定生产周期内所需加工工件的批次数和批量已知;②每批工件的刀具类型和刀具数量确定;③同类工件在各设备上的加工时间已知;④各工件优先级相同,不存在抢先生产;⑤每批工件种类相同,各子批一旦开始加工就不可中断,且不能被再次分割;⑥同一时刻每台设备只能加工一个子批;⑦同一设备换刀加工不同工件时,工件的加工顺序不同,换刀时间也不同;⑧所有设备上的第一个子批不需要调整,所要加工的工件均已准备好。
为便于对求解问题进行准确描述,引入下述符号和变量:
(1)输入条件
N为批量数N={j|1,2,3,…,N};
M为机器数M={i|1,2,3,…,N};
Lj为工件j的最大分批数;
Pj为工件j的加工时间;
Qj,k为工件j到k间的换刀设置时间;
dj为工件j的交货时间;
wr为拖期完工的权重系数;
we为提前完工的权重系数;
V为一个极大的正数;
t为机器上的加工序列。
(2)输出条件
Nj为工件批量数;
Bj为整数变量,工件j的实际分批数;
Oi,t为连续变量,机器i上序列t的开始时间;
Ci,t为连续变量,机器i上序列t的结束时间;
ETj为连续变量,工件j的r子批提前期;
DTj为连续变量,工件j的r子批拖期;
Fj,r为整数变量,工件j的r子批的批量数;
Wj,r为0-1变量,若工件j分了r批则Wj,r为1,否则为0;
Xi,t,j,r:0-1变量,如果工件j的r子批在机器i的t序列加工为1,否则为0。
(3)目标
Cmax为连续变量,最大完工时间;
Z为连续变量,交付时间偏差最大值。
基于上述定义,构建如下批次受限的双目标并行机分批调度模型:
(1)目标函数 最大完工时间是车间调度问题的常用目标,能表达车间的整体生产效率。此外,一批工件常常是源自一个订单、一个客户,若部分工件先交付,另一部分再交付,不利于所加工产品的运输和交付,也给客户增加了麻烦。因此,将每批工件各子批交付时间与计划交货期进行对照,得到提前与拖期权重和,即交付时间偏差。最大交付时间偏差的最小化,能保证一批工件同时、准时进行交付。同时,进行完工时间和交付时间偏差最大值的最小化,可实现双目标优化。
F=min(Cmax,Z)。
(1)
Cmax≥Ci,t,∀i∈M,t∈[1,2,…,N];
(2)
(3)
(2)提前与拖期值计算 在精益生产中,提前或是拖期生产都被定义为对资源的浪费。限制提前期,可以避免因过度提前完工而增加的库存或产品变质等风险;限制拖期,可以减少延期交付而带来的经济或名誉损失。
ETj≥dj-Ci,t-V×(1-Xi,t,j,r),
∀i∈M,j∈N,r=Bj,t∈[1,2,…,N];
(4)
DTj≥Ci,t-dj-V×(1-Xi,t,j,r),
∀i∈M,j∈N,r=Bj,t∈[1,2,…,N]。
(5)
(3)等量分批策略 每个子批的批量相同。考虑到可能出现工件总数无法均分为指定批次数的情况,在等量均分基本原则上进行一定调整,具体操作为:前Bj-1个子批的数量为该工件总数除以实际批数后取整,最后一个子批批量等于该工件总数减去前Bj-1个子批的工件数。
1≤Bj≤Lj,∀j∈N;
(6)

(7)
(8)
(4)机器分配策略 对于每一批工件来说,需要前一个子批划分后,后一个子批才可划分。已经划分的每一个子批需且必须分配到一台机器的某个事件点上进行加工。每台机器的每个事件点上最多可以加工一个子批。而对每台机器的两个连续事件点,一定是已经给前一事件点安排加工任务后,后一个事件点才可启用。若同一批次的两个子批分到同一台机器上,不允许连续加工,若连续加工即可视为一个子批。
(9)
(10)
(11)
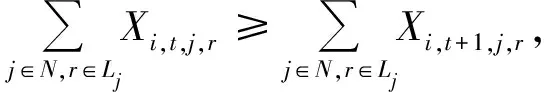
∀i∈M,t∈[1,2,…,N);
(12)

∀i∈M,j∈N,t∈[1,2,…,N)。
(13)
(5)计算完工时间 计算每个子批的完工时间,且在同一台机器上预留出前后两个子批之间的生产切换时间。
Ci,t-Oi,t≥Pj×Fj,r-V×(1-Xi,t,j,r),
∀i∈M,j∈N,r∈Lj,t∈[1,2,…,N];
(14)
Ci,t-Oi,t≤Pj×Fj,r+V×(1-Xi,t,j,r),
∀i∈M,j∈N,r∈Lj,t∈[1,2,…,N];
(15)
Oi,t+1-Ci,t-Qj,k≥
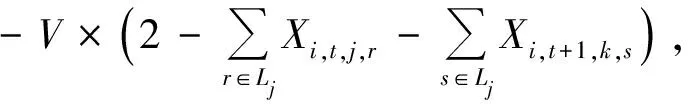
∀i,k∈M,j∈N,r,s∈Lj,t∈[1,2,…,N]。
(16)
上述问题是NP-难问题[11],若使用精确求解算法,很难在可接受的时间内找到最优解。求解本问题的难度在于如何确定每批工件的最优分批数量,如何改进算法满足刀具等各种约束,以及在问题规模较大的情况下如何高效求解本问题。
3 改进多目标鲸鱼群算法
针对批次受限的并行机分批调度问题,采用由高亮等[12]提出的鲸鱼群算法(WSA)进行求解,该方法因全局寻优能力较强而被广为应用。在WSA中每个个体会积极地向距离该个体“较优且最近”的鲸鱼移动。移动公式为:
(17)
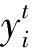
批次受限的并行机分批调度问题是一种离散组合优化问题。然而,WSA主要用于求解连续性函数问题,不能直接求解离散型问题。为求解批次受限的多目标并行机分批调度问题,需要根据问题特征,对WSA进行相应的改进,主要有:①设计批次受限的子批生成策略及排序的双层编码方式;②设计采用汉明距离表示个体间的距离;③融入多点保留交叉策略,设计个体移动规则;④提出随机邻域搜索与非劣个体选择策略。下文将详细阐述这些改进点。
3.1 批次受限的子批编码、解码及排序策略
工件实际分批数不定会导致:①使用传统编码方式时,个体编码长度无法确定;②固定工件子批的位置使用机器号编码时,机器上子批排序难以表达。针对以上问题,引入虚拟占位符[14],设计允许批次数可变的定长编码、采取双层分段的编码方式来表示问题的解。首先编码的长度由所有工件的最大分批总数之和决定,编码中第一层为机器编码,如图2所示工件号下包含的3个位置编码表示该工件最大可分为3批,数字表示第几台并行机器,当机器编码为虚拟占位符0时,表示工件未达到最大分批,此时子批的数量为总批量除以实际分批数;当工件完全分批时,子批的数量为总数除以最大分批数。第二层为加工顺序编码,随机生成工件位置排序的概率,机器上加工顺序由随机概率大小决定,概率小的优先在该机器上加工。编码与解码方式如图2所示。

3.2 “较优且最近”鲸鱼引导个体寻找
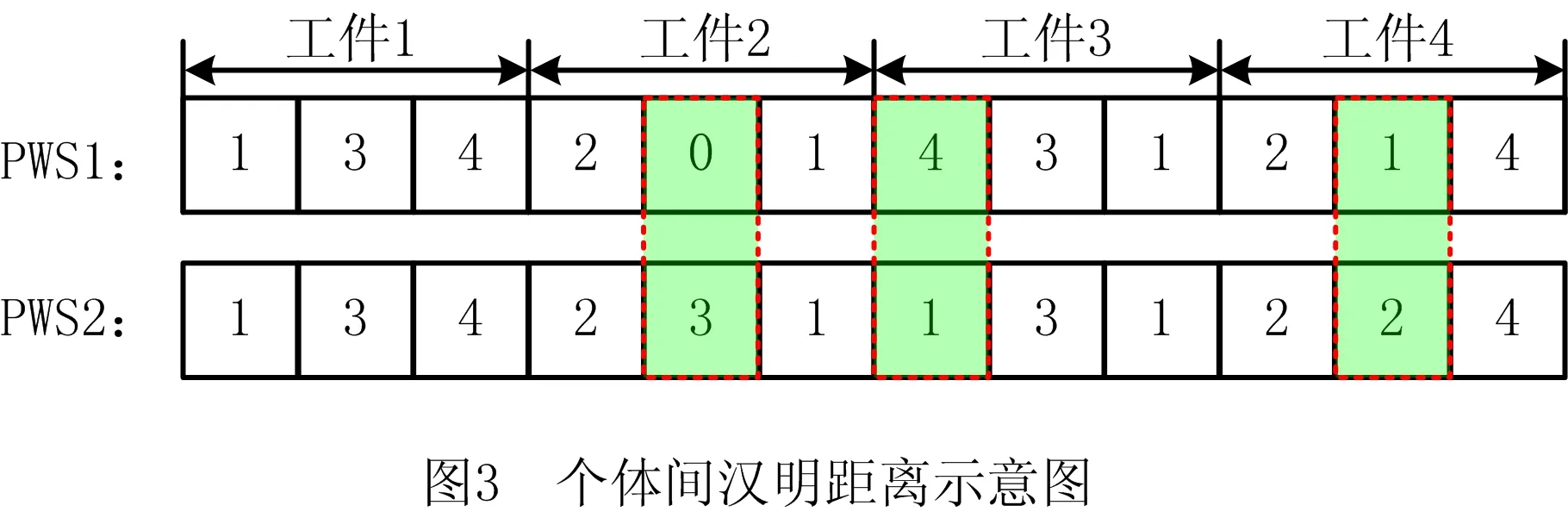
寻找“较优且最近”的鲸鱼个体,用其引导其他个体移动,是本算法最重要的步骤之一。为此,需要针对每个个体,依据汉明距离找出距离它最近的优秀个体。其中,汉明距离计算方法如图3所示。假定两个个体向量PWS均包含12个元素,从标记的部分可以看出向量PWS1和PWS2有3个元素不同,因此两向量之间汉明距离就是3。而较优个体的判定标准是Pareto支配关系。当且仅当其他个体处于前一Pareto层级,才判定其比当前个体更为优秀。
随机在种群中选一个个体作为父代,并在种群寻找另一个与父代个体“较优且最近”的引导个体,以汉明距离找出“最近”,以非支配排序等级作为“较优”。寻找“较优且最近”引导鲸鱼个体的伪代码如下所示:
算法1寻找“较优且最近”的鲸鱼。
输入:鲸鱼群Ω,鲸鱼Ωu;
输出:鲸鱼Ωu的“较优且最近”的鲸鱼。
1:开始
2:定义初始化为0的整数变量v;
3:定义一个初始化为无穷大的浮点变量temp;
4:while 终止条件不满足do
5:fori=1to|Ω|do
6:iff(Ωi) 7:v=i; 8:temp=dist(Ωi,Ωu); 9:end if 10:end for 11: end while 12:返回Ωv; 13:结束 在PM-ELSP中,不仅要划分批量为若干子批,给子批分配机器,还需要对分配到机器上的各子批进行合理的排序。本文算法引入多点保留交叉[15](Multipoint Preservative Crossover,MPX)策略来设计个体移动规则,寻找子批的最优排产策略。如图4所示,旧个体以及引导个体“较优且最近”的机器编码。引导移动从而产生的新个体机器编码如图4最下方分段编码所示。移动规则具体为如下步骤:①随机生成一组0和1组成的随机数,长度为各工件最大分批数的总和;②原个体中子批元素对应随机数为1的不变(图4中原个体虚线框部分),对应随机数为0的存储到新建集合O中;③将引导个体中所有属于集合O的子批元素依次填入到原个体,得到新的个体。第二层加工顺序编码跟随机器编码而变。 无论是在父代个体向引导个体移动阶段还是邻域搜索阶段,都会产生一个子代新个体。然而,并不是所有新个体都需要保留在子代种群,因此提出非劣个体保留策略,即当子代个体不劣于父代个体时,就保留在子代种群中,伪代码如下: 算法2新个体选择策略伪代码。 输入:父代个体X、子代新个体X′; 输出:新个体子代种群OffSpringPop。 1:开始 2: ifX′Xthen 3:X′加入到OffSpringPop 4: else ifXX′then 5:Xcount++ 6: else then 7:X′加入到OffSpring 8:Xcount++ 9: end if 10:返回OffSpringPop 11:结束 其中:OffSpringPop表示在算法迭代过程中产生的新个体子代种群,X′X表示新的个体X′支配X。 Pareto将无法直接比较的多个目标函数的优化问题进行归纳,数学公式如下所示: max/minF=f(x)=(f1(x),f2(x),…,fm(x))。 (18) s.t. gi(x)≤0,i=1,2,…,p; (19) ej(x)=0,j=1,2,…,q。 (20) 式中:x=(x1,x2,…,xn)T为决策空间Ω中的一个n维决策向量,F是m个目标函数(f1(x),f2(x),…,fm(x))T组成的一个m维的目标向量,gi(x)≤0定义了p个不等式约束,ej(x)=0定义了q个等式约束。 算法3MOWSA。 输入:目标函数,鲸鱼群Ω; 输出:全局最优解。 1:开始 2:初始化参数; 3:鲸鱼种群初始化并评价; 4:初始化Pareto外部存档; 5:while 终止条件不满足do 6:fori=1to|Ω|do 7:寻找Ωi的“较优且最近”的鲸鱼Y;//算法1 8:if Y存在then 9:生成鲸鱼Ωi的副本X′; 10:副本X′根据个体移动规则向Y移动; 11:评价新副本X′; 12:else 生成鲸鱼Ωi的副本X″; 13:按照领域搜索策略对副本X″进行领域搜索; 14:评价新副本X″; 15:end if 16:SelectIndividual(OffSpringPop,Ωi,X′);//算法2 17:ifΩi.count≥Ts 18:重新初始化Ωi,并进行评价; 19:end if 20:i=i+1; 21:end for 22:父代、子代种群合并; 23:非占优排序并更新种群; 24:更新Pareto外部存档; 25:end while 26:返回全局最优解; 27:结束 为验证MOWSA在求解PM-ELSP问题方面的有效性,从http://www.cima.uadec.mx/instancias/中选用包含大中小规模的15个实例进行实验。同时,将其与解决多目标优化问题常用的带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm,NSGA-Ⅱ)[16]、多目标人工蜂群算法(Multi-objective Artificial Bee Colony algorithm,MOABC)[17]与改进后的MOWSA算法进行比较。对所有算法参数进行统一设置,最大迭代次数Maxiter=200,种群P=50,Pareto外部存档的大小设置为50,每个算例运行10次。 为评价多目标优化算法,通过查阅相关文献,选取以下评价指标。世代距离(GD),其值越小表示算法性能越好。反世代距离(IGD),其值越小表明算法的收敛性和多样性比较好。非支配解的个数(NDS),其值越大表明算法的效果越好。超体积指标(HV),算法获得的非支配解集与参照点围成的目标空间中区域的体积。HV值越大,说明算法的综合性能越好。 三个算法各独立运行10次,同时选取各评价指标的最小值(min),最大值(max),平均值(agv),标准差(sd)进行分析。比较结果如表1~表4及图5所示,表中加粗数据表示案例中性能较好的指标值。 表1 世代距离(GD) 表2 反世代距离(IGD) 表3 非支配解的个数(NDS) 表4 超体积指标(HV) 从测试指标IGD的8组数据箱线图如图5所示,可以看出,大多数时候MOWSA比NSGA-Ⅱ、MOABC小,意味着MOWSA比其他两种算法获得的解有更好的收敛性,MOWSA在15组实例验证下,表现都优于其他两种算法,可以看出MOWSA不但收敛性好,而且分布均匀。 图5中IGD的测试结果箱型图可见,MOWSA算法所获得解的上、下四分位数或中位数,均小于NSGA-Ⅱ和MOABC算法所得的解,证明增加非劣个体保留策略后,MOWSA算法更好地跳出了局部最优。 从表3所示的非支配解个数来看,MOABC在多数情况下只能取得1~2个非支配解,而在大中小不同规模的算例中,MOWSA可以获得多个非支配解,其数目远大于NSGA-Ⅱ和MOABC。分析可见,MOWSA算法中设计了融入多点保留交叉策略的个体移动规则,增强了解的多样性,从而保证了MOWSA能获取到PM-ELSP的更多前沿解。 由表4测试结果可见,在多数情况下MOWSA超体积均大于两个对比算法,表明其在目标空间中获得非支配解集与参照点围成的区域体积更大,证明其前沿解的分布更均匀。 综上所述,在求解PM-ELSP问题时,改进的MOWSA算法在收敛性、多样性上显著优于对比算法,且得到的Pareto前沿解的分布更为均匀。 某次订单包含有13种型号的工件,各型号工件的数量、加工时间、刀具数量如表5所示,各型号工件间换刀时间如表6所示,该车间有6台并行机加工设备,由于实际生产中存在交货期限定,具体交货期dj随机产生, 表5 各型号工件的相关信息 表6 各型号工件间换刀时间 (21) 其中σ是介于0~1之间的随机实数。 将提前/拖期罚系数分别设置为WE=0.2,WT=0.8,算法相关参数如下:种群P=80,迭代次数Maxiter=300。 图6是3种算法所得到的Pareto前沿对比图,可以看出,3种算法的Pareto前沿一直处于优化状态,其中黄色三角形为MOWSA最终的Pareto最优解集,所包含的调度方案对应的两个目标函数值如表7所示,表中标黑的数据分别是图6中的A、B、C三点调度方案对应的目标值。图7给出了图6中A、B、C三个点的调度甘特图。从图6中可以看出,MOWSA的Pareto前沿要优于其余两种算法,说明MOWSA求解多目标问题是可行且有效的。 表7 前沿解集 图7分别是图6中对应3个点的调度方案甘特图,图中的子批表示J8.3或J13.1分别表示第8种工件第3个子批和第13种工件的第1个子批。由图可以看出,在最大完工时间最小时,其各个设备的利用率比较均衡,而当提前与拖期的权重和最小时,由于每个工件更偏向于按交期完工,导致设备的利用率比较不均衡。 本文通过分析多品种小批量的并行生产需求和加工中存在的刀具约束,凝练了批次受限的多目标并行机等量分批调度问题(PM-ELSP),以完工时间和交付时间偏差最大值的最小化为目标,以期同时达到高效、准时生产的目标。基于该问题特征,构建了数学规划模型,提出一种多目标鲸鱼群算法(MOWSA)。其中,设计了允许批次数可变的定长编码机制,保证了最大批次数限制下的子批划分;融入了多点保留交叉策略,以增强解的多样性;提出了非劣个体保留策略,以促进算法跳出局部最优。结果表明,所提算法能有效求解PM-ELSP问题,其性能优于对比算法NSGA-Ⅱ和MOABC。特别是在大规模算例中,算法表现出收敛速度快、前沿解个数多、前沿解分布均匀的优势。研究发现,相对于并行机调度,并行机分批调度更贴近实际,更有利于均衡设备利用率、缩短生产周期、提高生产效率、实现准时生产。为了更加符合生产实际,未来将在现有研究基础上,围绕具有可变批量和刀具指派的并行机分批调度问题进行研究。3.3 引入多点保留交叉的鲸鱼个体移动规则

3.4 邻域搜索及非劣解保留策略

3.5 Pareto外部存档
4 数据实验
4.1 性能评价指标
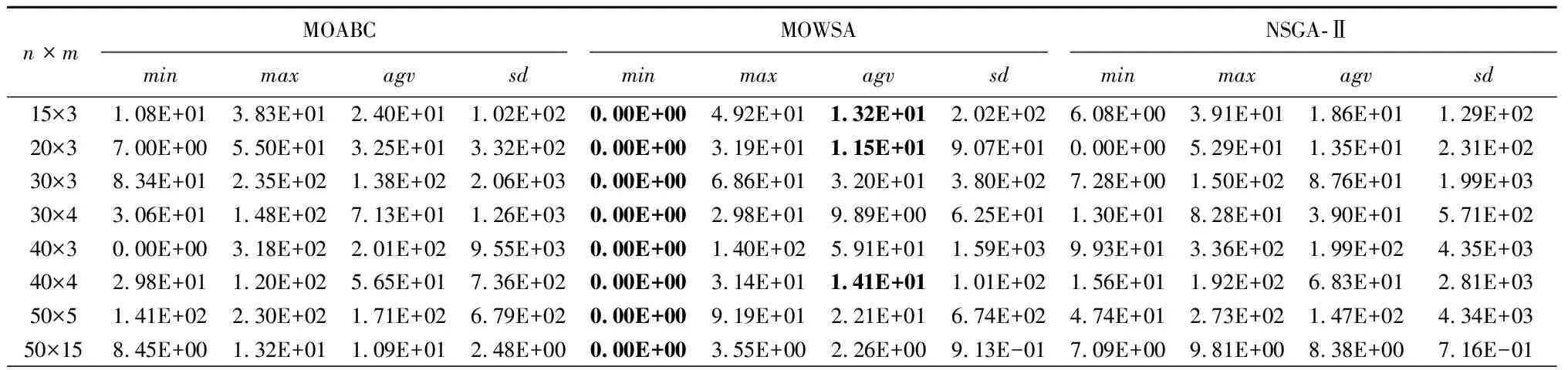
4.2 实验结果分析




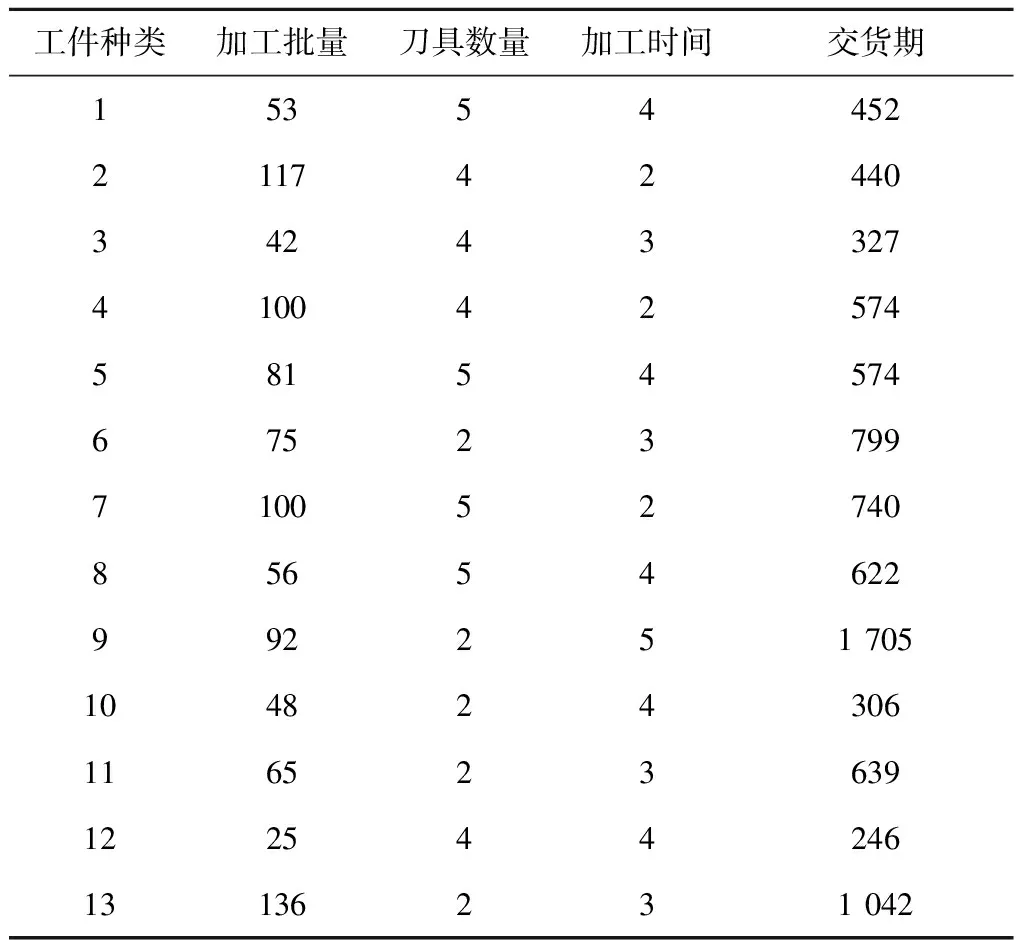
5 案例分析




6 结束语

