Identity-Based Encryption from Lattices with Small Cipher Size

WANG Ziqing, TANG Dianhua,2*, and LI Fagen

(1. School of Computer Science and Engineering, University of Electronic Science and Technology of China Chengdu 611731;2. The 30th Research Institute of China Electronic Technology Group Corporation Chengdu 610041)

Abstract Identity-based encryption (IBE) is very attractive because it does not have certificate management issues. However, the IBEs based on the bilinear Diffie-Hellman problem cannot resist quantum attacks. In order to ensure security under quantum attacks, lattice-based IBE is proposed. However, the existing lattice-based IBEs usually not only have a large ciphertext size but also can only encrypt a few bits of plaintext information in one ciphertext. In this paper, we propose a new lattice-based IBE scheme based on learning with errors (LWE) and its ring version. For the setting l=n, our scheme can encrypt the plaintext twice long of other schemes in one ciphertext. Then we prove that our scheme can achieve the indistinguishability of ciphertexts against adaptively chosen identity and chosen plaintext attack (IND-ID-CPA) in the random oracle.

Key words IBE; lattice-based cryptography; LWE; ring LWE Received date: 2022 - 01 - 04; Revised date: 2022 - 03 - 01

Identity-Based encryption (IBE) was first proposed by Shamir[1]in 1985. Compared with public key infrastructure (PKI), the public keys of users in IBE schemes are derived directly from identities like e-mail addresses or phone numbers instead of being generated by users. The private keys are generated and distributed to users by a trusted authority (TA) who has a master key. As TA will guarantee that the private keys are sent to the users with the corresponding identities, IBE does not have certificate management problems. The IBE schemes based on the bilinear Diffe-Hellman problem may face the threat of quantum attacks. However, since there is no quantum algorithm that can effectively solve the hard problems of lattice, the lattice-based IBE schemes are considered to be able to maintain the security under quantum attacks. In 2008, Ref. [2] proposed the first latticebased IBE named GPV, which is based on learning with errors (LWE) problem[3]. The scheme achieves indistinguishability of ciphertexts against adaptively chosen identity and chosen plaintext attack (IND-IDCPA) under random oracle. The random oracle model assumes that the adversary can not attack the hash function and the standard oracle doesnot have this assumption, which means that the standard model has better security. In 2010, Ref. [4] proposed the first lattice-based IBE scheme under the standard model.However, the IBE schemes under the standard model have larger size of parameters and ciphertext than the IBE schemes under the random oracle. In the same year, Ref. [5-6] proposed some more efficient latticebased IBE schemes under the standard model. The above schemes use the trapdoor generation algorithm to generate a uniformly random matrix and a short basis. The trapdoor generation algorithm was proposed by Ref. [7] in 1999 and then improved by Ref. [8] in 2009. In 2012, Ref. [9] gave a new method to generate trapdoors for lattices. The size of the output matrix of their algorithm is smaller than that of previous work.They also gave the trapdoor generation algorithm that can be used for ring. To reduce the size of public parameter and ciphertext, in 2016, Ref. [10] proposed an IBE scheme based on RLWE. In 2018, Ref. [11]proposed another RLWE-based IBE scheme with smaller ciphertext size than Katsumata’s[10]. Ref. [12]proposed a RLWE-based IBE with short parameters in 2020. The encryption of the above schemes can be seen as a variant of dual Regev PKE[2], which makes these schemes have large ciphertexts.

In this paper, we propose a new LWE-based IBE scheme with a small size of ciphertext. We also give the ring version of our scheme. The proposed scheme is IND-ID-CPA secure under the random oracle.Compared with GPV[2], if we set the parameterl=n,the length of the plaintext that our scheme can encrypt is twice of GPV’s[2]without the increase of ciphertext size.

1 Preliminaries

1.1 Notation

The base of logarithmic used in this paper is always 2. We use Zqto represent Z∩[0,q) whenqis a positive integer. ■r■ represents the nearest integer of the real numberr. When the value ofris the middle value of the two nearest integers, it is rounded up.■r」represents round down operation. We use lowercase bold letters to represent column vectors, such as a.Specifically, 0 represents the zero vector. We use |r| to represent the absolute value of the numberr. The dot product operation of vectors is represented as 〈·,·〉.x←Dmeans thatxis sampled from the distributionD. WhenDis a finite set, it means being uniformly sampled fromD. In particular, we useDZq,σto represent a discrete gaussian distribution with the parameter σ on Zq. We use capital bold letters to denote matrices. | |·||∞represents the infinite norm and||·||represents the Euclidean norm. The Gram-Schmidt order orthogonalization of matrixAis denoted byA˜. We useRqto represent Zq[x]/(xn+1).

1.2 Lattices and Hard Problems

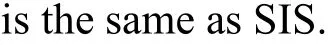
It has been proved that the decision LWE problem is as hard as some worst-case hard problems onn-dimensional lattices under a quantum reduction.

Ref. [15] proved that whens←DZnq,αq, the LWE problem is still hard. This form of LWE is called normal form LWE.

Definition 4[16](ring learning with errors(RLWE)) For integersn≥1,q≥2, a real number α ∈(0,1), a uniformly random elements∈Rq, we can define a distribution R LWEn,q,αoverRq×Rqas this:

wherea←Rqande←DRq,αq.

The RLWE problem and its normal form have also been proved as hard as some worst-case hard problems on lattices under a quantum reduction.

1.3 Algorithms

The paper introduces some algorithms for lattices which are important for building a encryption scheme.

Lemma 4[18]There exists a PPT algorithm SamplePre(a,Ta,u,σ) that can output a vectorx∈Rmqwhich satisfiesaTx=uand follows a discrete gaussian distribution of parameter σ.TAis the trapdoor ofa.

2 The IBE Scheme

The IBE scheme uses the TrapGen and SamplePre algorithms to generate the master public key, master secret key and users' secret keys, which is similar with other LWE-based IBE schemes. The main difference between our scheme and others is in the encryption. Compared with other LWE-based schemes, the first part of ciphertexts of our scheme can also encrypt messages. While other schemes only encrypt the message in the second part of ciphertexts.This makes our scheme encrypt more bits than other schemes. To encrypt messages, our scheme uses LWE instances to mask the plaintext. As the LWE instances(A,As+e)are indistinguishable from uniformly random,As+e+ΔmandAs+e+AΔmwill also be indistinguishable from uniformly random vector,where Δ isq/2.

2.1 Construction Based on LWE

Our IBE scheme is described as follows:

Setup(1λ): The PKG chooses an odd prime numberq＞2, positive integersn,m,l,k, a real number σand a hash functionsH:{0,1}k→Znq×n×Znq×l, wherekis the length of an identity andlis the length of the second part of message. The first part of the output ofHis an invertible matrix. Then it runs TrapGen(n,m,q)to generate a uniformly random matrixA∈Znq×mand a short basisTA∈Zmq×mof the lattice Λ⊥q(A). The PKG sets the master public key mpk=Aand master secret key msk=TA. Finally, the PKG publishes the parameters p aram=(n,m,l,q,σ,A,H).

2.2 Correctness

Theorem 1 The decrypt algorithm can recover the message from ciphertext correctly if the following inequations are hold.

2.3 Security

We first give the definition of IND-ID-CPA.Then we prove that our scheme can achieve IND-IDCPA security.

Definition 5 For a IBE scheme P(Setup,Extract, Enc, Dec), a challengerCand an adversaryA,the IND-ID-CPA game is described as follows.

SetupCruns the Setup algorithm to generate the public parameters param, master public keympk and master secret key msk, then sends param andmpk toA.

Phase 1Acan make secret key extraction queries for any identity id. The challengerCruns Extract(p aram,id,msk ) to generate the secret keysk and sends it toA.

ChallengeAselects an identity id*which has not been queried in phase 1 and two different messagesm0,m1and sends them toC.Crunsc←Enc(p aram,id*,mb) and responsesctoA, wherebis a uniformly random bit.

Phase 2Acan repeat Phase 1. The only restriction is that he can’t query the secret key of i d*.

GuessAoutputs a bitb′.

If there does not exist any polynomial adversaryAthat achieves non-negligibleAdv(A)=|Pr[b′=b]-Pr[b′≠b]|, we say thatPis IND-ID-CPA secure. If the target identity is submitted before the setup, the game is named indistinguishability of ciphertexts against selectively chosen identity and chosen plaintext attack(IND-sID-CPA).

Theorem 2 If there exists a polynomial adversaryAthat can break the IND-ID-CPA secure of the scheme described in section 3.1 in the random oracle model, then there exists a polynomial algorithm that can solve the normal form decision-LWE problem.

Proof We show that how to use the adversaryAto construct an algorithmCthat can answer the normal form LWE oracleO. We setCto be the challenger of the IND-ID-CPA game. First,Cqueries the oracleOand getsm+linstances (ai,bi)∈Znq×Zq. ThenCuses these instances to combine two matricesA1∈Zmq×n,A2∈Zlq×nand two vectorsb1∈Zmq,b2∈Zlq,where every row of matrices isaiand every component of vectors isbi. The rank of the matrixA1must ben. If not,Ccan repeat the query until he gets a ranknmatrix. After this,Cperforms the game withAas follows.

SetupCgenerates the public params of the IBE scheme as follows.

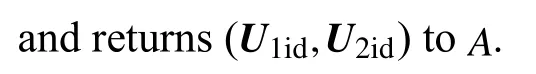
Secret key queries WhenAqueries the secret key for an id,Csearches the saved tuple (Q,id,U1id,U2id,S1id,S2id) from the history of the hash oracle query. (We assume that every id has been queried in hash query before secret key query.) IfS1id=⊥ andS2id=⊥,Caborts and outputs a random bit. Else,Creturns (S1id,S2id) toA.

If the instances returned byOare uniformly random vectors, the challenge ciphertext is uniformly random and completely hides the information ofb. If the instances returned byOare normal LWE instances,then the challenge ciphertext will be a valid encryption of mbfor identity i d*.

Acan make more secret key queries after the challenge phase with the restriction that it can’t make the secret key query for identity id*. After that,Aoutputs a bitb′toC. Ifb′=b,Coutputs 1, elseCoutputs 0.

IfCdose not abort, the interaction between oracleO, algorithmCand adversaryAwill be as shown in Figure 1.

By a standard argument,Cwill not abort during the game with the probability 1/QH. IfCdoes not abort, it means that the target identity submitted byAis the identity queried by theI-th hash query. In this case, if the challenge ciphertext is uniformly random,the probabilityb′=bis 1/2. (Which means that the instances returned byOare uniformly random.) If the challenge ciphertext is a valid encryption, the probabilityb′=bis 1/2+Adv(A). (Which means that the instances returned byOare LWE instances.) So the advantage thatCcan distinguish LWE instances from uniformly random vectors is Adv(A)/QH. Thus, ifAhas an non-negligible advantage to break the IND-IDCPA security, thenChas a non-negligible advantage to solve decision normal LWE problem.

Fig. 1 The interaction between O,C and A.

2.4 Construction Based on RLWE

Our ring version IBE scheme is described as follows:

Setup(1λ): The PKG chooses positive integersn,m,q,k,l, two real number σ,θ and a hash functionsH:{0,1}l→Rq×Rq, wherelis the length of an identity. The first part of the output ofHis an invertible element ofRq. Then PKG runs TrapGen(n,m,q,θ) to generate a random vectora∈Rmqand a short basisTa∈R(qm-k)×kof the lattice Λ⊥q(a). The PKG sets the master public key mpk=aand master secret key msk=Ta. Finally, the PKG publishes the parametersparam=(n,m,l,q,k,σ,θ,a,H).

The proof is similar as that in section 3.2, so we omit it.

Assume that the decision-RLWE problem is hard,the ring version IBE is IND-ID-CPA secure. The proof of the security of the ring version IBE is similar as that in section 2.3, so we omit it.

3 Comparison

We compare the correctness conditions for our scheme with the conditions for GPV[2]and ABB[5]. The security model and the error term in the decryption results of our scheme, GPV[2]and ABB[5]are listed in Table 1. (The schemes used for comparison are multi bits encryption version.)

Table 1 Correctness condition of three schemes

The correctness condition of our scheme is similar with GPV[2]. The difference between GPV[2]and our scheme is that our scheme needs to guarantee the second inequation. As we can set the distribution parameters of secret random vectore1to be the same as the distribution parameters ofe2, the second inequation will always hold as long as the first inequation holds. Thus, the parameter setting of GPV[2]can be used for our scheme without losing correctness and security. ABB[5]has more decryption noise because of the standard model. The length of the error term used in ABB's[5]encryption is 2m. The distribution of the outputs of S ampleLeft is the same as the outputs of S amplePre except the length of outputs.Therefore, the parameter setting that guarantee the correctness of ABB[5]can also guarantee the correctness of our scheme.

Compared with other lattice-based IBE schemes,our scheme can encrypt more bits in a ciphertext,which means that our scheme can achieve smaller ciphertext size than other lattice-based IBE schemes when the length of the plaintext is fixed. To encrypt more bits, the size of secret key of our IBE scheme is bigger than that of other schemes. However, the ratio of the size of secret key to the size of plaintext is not greater than that of other schemes. The comparison of the ciphertext size, secret key size and plaintext size is shown by Table 2. To encryptklbits, one can just divide it intokpieces and encrypt each piece to getkciphertexts. However, the ratio of the ciphertext size to the plaintext size of each scheme will not be changed,as every ciphertext only corresponds to a piece of plaintext withlbits.

Table 2 Comparison of ciphertext size, secret key size and plaintext size

When the parametersn,m,l,qof schemes are chosen, our scheme can encryptl+nbits in a ciphertext whose size is (m+l)logq, while other LWEbased schemes can only encryptlbits in a ciphertext with the same ciphertext size. Ifl=n, the length of message that our scheme can encrypt is twice of other schemes, and the size of the ciphertext is not bigger than that of other schemes.

The disadvantage of our scheme is the computation cost. Our scheme needs to perform one more discrete gaussian sampling and vector addition in encryption than other schemes. In decryption, our scheme needs to perform two more matrix multiplications, and one more vector subtraction.However, as our scheme is able to transmitnmore bits, we think the performance penalty of adding these computations is acceptable.

4 Conclusion

In this paper, we propose an IBE scheme and its ring version based on LWE/RLWE problem and prove that our schemes is IND-ID-CPA secure under the random oracle model. Compared with previous latticebased IBE schemes, the computation cost of encryption and decryption of the proposed schemes is more than others, but our schemes can encrypt more message without increasing the size of ciphertext.