雷达强降水数据小波域统计特征及其与环境参数的关系研究

杨春生 寇蕾蕾 ,2 蒋银丰 陈垚 毛赢 王振会 , 2

1 南京信息工程大学大气物理学院, 南京 210044

2 南京信息工程大学气象灾害预警与评估协同创新中心, 南京 210044

3 福建省平潭综合实验区气象局,平潭, 350400

1 引言

强对流天气是影响我国的主要灾害性天气之一，往往引起严重的自然灾害，对我国人民的生活及经济财产造成严重损失，而强降水是强对流天气的重要表现形式之一，强降水时空结构特征的提取及强降水的精确估计对气象、水文及旱涝灾害预报预警等都具有十分重要的意义。我国地处东亚季风气候区，干旱洪涝灾害频繁发生，且受大气运动、海陆位置、复杂地形等多种因素及其相互作用的影响，降水尤其中小尺度强降水具有复杂的时空变异性，呈现复杂的多尺度空时统计结构特征（Harris et al.,2001; Sorooshian et al., 2011; 章国材, 2011）。因此，研究并建立中小尺度强降水的先验特征模型，对中小尺度强降水精准估计和预报具有重要的现实意义。

小波变换是对信号进行不同尺度不同方向的带通滤波，具有良好的多分辨率性、时频局部分析特性及能量聚集性等特征（Perica and Foufoula-Georgiou, 1996; Wainwright and Simoncelli, 1999），一般自然图像在小波分解后易呈现出稳定一致的规律性，常常具有非高斯、多分形、局部相关等统计特征（肖志云, 2004; Wang et al., 2014）。对于二维雷达强降水回波场来说，强降水单体常常群簇在一片弱降水中，表现出高度聚集性、稀疏相关性及方向边缘性特征，使用小波变换能很好地刻画雷达强降水数据的多尺度统计结构（Kou et al., 2020）。Huang and Mumford（1999）研究也指出自然过程的图像在尺度上表现出变异性，通常表现为孤立的奇点，即边缘或活动剧烈的嵌套区域的形式，在不同方向上使用一组多尺度带通滤波器对于提取图像的局部跳变以及不连续性非常有用。利用傅里叶变换和小波变换分析强对流降水回波的频域多尺度统计结构，观察降水场的非高斯重尾特性、高阶统计矩的尺度参数研究，揭示降水过程的二阶统计量在不同尺度上的变化形式（Ebtehaj and Foufoula-Georgiou,2011a, 2011b; Ebtehaj, 2013; García and Koike,2016），也可利用降水的多尺度统计特征建立时空降水的简约随机模型来量化降水的变化，并分析降水场的特征（Lovejoy and Schertzer, 2006;Venugopal et al., 2006; Mandapaka et al., 2010）。

为更好地抓住降水数据结构这些重要的统计特征，前人将描绘自然图像的高斯尺度混合模型引入到天气雷达数据建模中，且此模型应用到了地基和星载雷达降水融合中（Ebtehaj et al., 2012;Ebtehaj and Foufoula-Georgiou, 2013）。使用小波变换的降尺度方法来研究降水场的小波域特征，揭示小波系数的稀疏性，计算出的相关系数、统计矩、决定系数以及空间模式，发现降尺度方法的输出与观测到的降水场之间具有良好的一致性（Foufoula-Georgiou et al., 2014; Nourani et al., 2020）。寇蕾蕾等（2019）基于雷达降水数据空间域统计特征，采用小波域高斯尺度混合模型来构造雷达回波强度数据先验模型，并将其应用到天气雷达图像插值中，得到能有效反映强降水回波及小尺度变化细节的高分辨率雷达回波强度图像，用于提升降水回波的分辨率。前人的工作多在于个例的研究，而本文是基于多年雷达数据进行小波域的统计特征及其与环境参数的关系分析，为强降水小波域统计特征参数化建模提供依据。

本文选取合适的小波函数对雷达强降水回波进行多尺度分解，首先讨论和统计了多年强降水小波域的非高斯重尾特性，并采用广义高斯分布来表征其非高斯分布。其次讨论了强降水小波系数多分形特征，并分析了不同形态回波雷达强降水分形特征参数的相似性和差异性，以及与非高斯重尾分布特征参数的关系。最后，基于再分析资料的环境参数，利用多回归分析法建立强降水小波域不同方向小波系数分形参数与环境参数的关系，说明强降水统计特征参数与物理参数的关系。建立符合物理背景的雷达强降水先验信息，并合理地利用先验信息对强降水做出精准的估计和预报，对雷达数据处理、降水数据在气象与水文方面的应用都具有十分重要的理论和实际意义。

2 雷达强降水回波小波域统计特征

2.1 数据及方法

本文选用的是江苏省南京市2013～2016年每年4～10月的S波段雷达数据，此雷达完成一次体扫所需要时间6～7 min，能够真实且不间断地监视对流降水的发生发展过程。首先筛选独立的降水事件，降水事件为雷达所能探测到较为完整的对流发生发展过程，部分为雷达探测距离问题只能探测到对流的旺盛时段，在对流旺盛阶段雷达显示至少一个强回波中心，且最大回波反射率因子需大于45 dBZ，最后共筛选了180次的独立降水事件数据，降水事件历经过程多则2天，少则3～4小时。其次针对降水事件数据，挑选雷达所探测到对流最旺盛阶段时刻的回波场，此回波场要能够较好显示出对流所发生的轮廓，边际分明，且强回波中心区域呈现某种形状（单体状回波，块状回波，离散状回波，线性回波）。最后，便于直角坐标系下的数据处理，采用3次线性插值将雷达体扫数据重采样到笛卡尔坐标系后的2 km等高平面回波显示（CAPPI），其网格化分辨率为1 km × 1 km。

为提高雷达数据质量，采用滑动的窗口去除雷达回波孤立点，对地物杂波进行物理去除。在雷达数据预处理基础上，采用一种非抽样平稳离散小波变换（SWT）对强降水雷达回波场进行分解，选择“Haar”小波基，它在分解时去除“下采样操作”，消除“频率混跌项”，不会因为重构处理带来虚假回波，同时在进行小波系数的统计分析时去除无用背景零点（无降水回波）的影响，保留了因分解过程中与滤波器卷积作用而生成的有用零点（Nason and Silverman, 1995）。

2.2 雷达强降水回波小波域重尾性分布特征

对于雷达降水回波，强降水单体常常群簇在一片弱降水中，表现出高度聚集性、稀疏相关性及方向边缘性特征（Kou et al., 2020）。利用小波变换可以很好地表达强降水的多尺度过程，获取强降水局部不连续性或起伏变化等细节特征，这对多尺度的降水不连续性进行量化是非常有用的（Azam et al., 2014）。实验表明均匀的降水图像在小波域会表现出接近为零的小波系数，而对于回波分布不均匀的强降水图像，在小波域表现出小波子带的中心有一个尖峰（零值附近），如雷达降水数据的群聚性在小波频率域，常表现出明显的小波系数分布的尖峰和重尾特性，称为非高斯重尾特征，其两边延伸的值无法用高斯框架进行建模（Ebtehaj and Foufoula-Georgiou, 2011a）。

对2015年6月30日南京地区一次雷暴过程个例分析（图1a），其回波显示在雷达站点东北方向100 km处有强的单体生成，周围并伴有较多的弱回波。强对流回波场经小波分解后的水平向子带的小波系数（图1b），对应原始场（图1a）中水平向细节信息，它捕获的是原始场水平方向的不连续性及起伏变化特征，经数学统计后水平子带小波系数的概率分布统计（图1c），再取对数后的概率分布统计（图1d）。由图1d可看出水平方向子带雷达图像的小波系数的概率分布均呈现为大量小值和少量大值的构成形式，数值方差较大，即非高斯“重尾”特性（其它方向子带类似）。这种重尾性反映了降水回波中的小尺度变化及一些强回波奇异值，这是对雷达回波强度数据建模时需要注意的一个重要特点（寇蕾蕾等, 2019）。

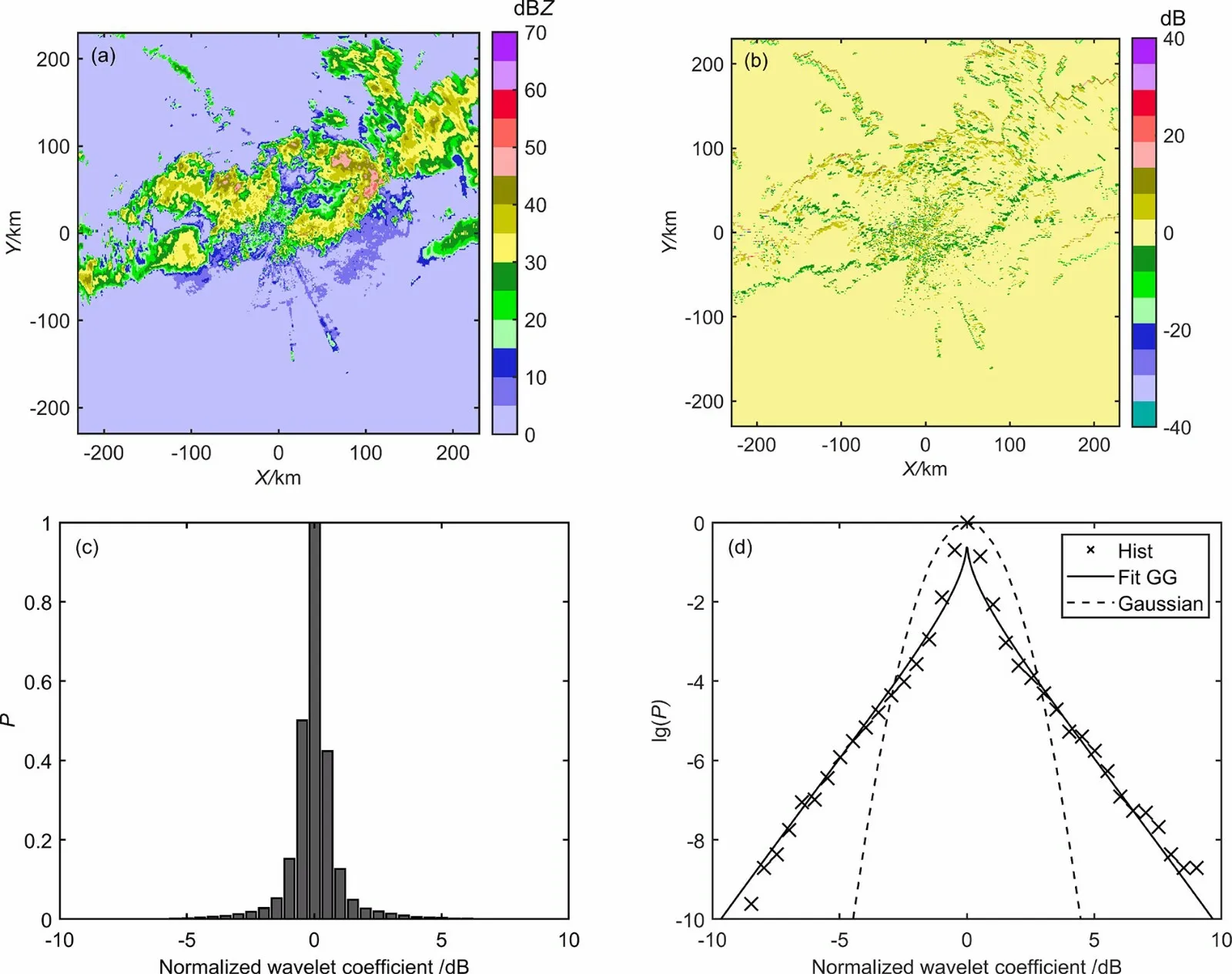
图1 2015年6月30日00时16分（协调世界时，下同）（a）南京降水个例回波强度、（b）一级分解得到的水平子带小波系数以及（c，d）标准偏差归一化后水平子带小波系数的概率统计分布 [P，lg (P)]。雷达强降水反射率因子图像的小波域小波系数概率分布（Hist）比常规高斯分布（Gaussian）两边的值更多/更大，图（d）中的实线是拟合的广义高斯分布（Fit GG）Fig. 1 (a) Radar reflectivity image of the precipitation case in Nanjing at 0016 UTC June 30, 2015, (b) wavelet coefficients for horizontal sub-band of the reflectivity image in (a), and (c, d) the statistical probability distributions of the horizontal sub-band wavelet coefficients normalized by the standard deviation [P, lg (P)] at one level of decomposition. The wavelet coefficient probability distribution (Hist) in the wavelet domain of the radar heavy precipitation reflectance image has a heavier tail than the Gaussian distribution (Gaussian). The solid line in (d) is the fitted generalized Gaussian distribution

雷达强降水数据的小波系数有非高斯重尾性、稀疏性特征，即小波系数由少量大值、大量小值（大部分为零或接近于零）构成，但不同的强降水数据的重尾及稀疏程度均不同。因为高斯分布容易平滑强降水的高阶统计特征和局部几何结构，从而丢失小尺度细节，所以采用广义高斯分布 [也称为广义拉普拉斯（Generalized Laplace）分布] 表征这种重尾和稀疏性，其小波系数经过中心化预处理，对于零均值广义高斯族可用形状参数α和宽度参数s表示为

基于180次独立降水事件，筛选出263个强降水回波场，其中一次降水事件可能有多种回波形状的强降水回波场。然后，在不同方向上讨论多年强降水数据小波域小波系数之间的差异性。从图2可以看出，强降水小波域小波系数重尾性参数α都在0.11～0.24之间，其水平向子带（图2a）、垂直向子带（图2b）分布较为均匀，具有明显的一致性，而对角向子带（图2c）重尾性参数α偏向于小值。在不同强度对流降水过程中，它们的重尾性明显程度也不一样，图3显示了强对流降水与弱对流降水回波非高斯重尾分布的差异性，强降水重尾性两边的小值出现的概率越大，零附近值出现的概率越小，α值为0.13（图3a），弱对流降水α值为0.21（图3b）。

图2 强降水回波场分解得到的（a）水平向、（b）垂直向和（c）对角向子带小波系数重尾参数α分布直方图Fig. 2 Heavy-tailed parameter α distribution histogram of (a) horizontal, (b) vertical, and (c) diagonal sub-band wavelet coefficients obtained from the decomposition of the heavy precipitation field

图3 （a）强对流与（b）弱对流一级分解后水平子带小波系数标准偏差归一化的概率统计分布（P对比。雷达强降水反射率因子图像的小波域小波系数概率分布（Hist）比常规高斯分布（Gaussian）两边的值更多/更大，实线是拟合的广义高斯分布（Fit GG）Fig. 3 Comparison of the statistical probability distributions (P) of the horizontal sub-band coefficients normalized by the standard deviation after first-order decomposition of (a) strong convection and (b) weak convection. The wavelet coefficient probability distribution (Hist) in the wavelet domain of the radar heavy precipitation reflectance image has a heavier tail than the Gaussian distribution (Gaussian). The solid line is the fitted generalized Gaussian distribution (Fit GG)

2.3 雷达强降水回波小波域多尺度分形参数特征

小波分解是一个数学工具，利用它可以很好地理解自然随机过程中的尺度行为，对于雷达回波二维降水场来说，利用二维离散小波变换则可在每个方向（水平向，垂直向和对角向）创建三个小波系数。强降水小波分解是不断增加幅值的过程，子带内的小波系数q阶矩可近似表示为如下关系（Abry et al., 2004）：

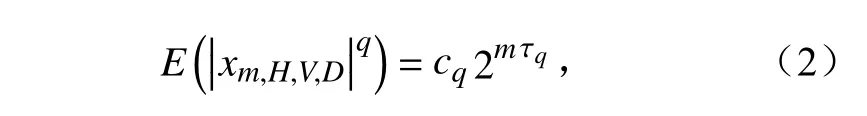
式中，m表示分解级数（如m=1～4，表示尺度2～16 km，图像原始分辨率为1 km）；H，V，D分别表示水平向、垂直向、对角向子带；cq表示常数因子；τq表示小波系数分形参数（反映了小波系数随尺度的大致变化规律）或者线性地表示qF，F为自相似指数，其中分形参数τ1、 τ2又分别表示小波系数的一阶矩（q=1，对应均值）和二阶矩（q=2，对应方差）。应该注意的是，较高的τq值表示相应小波系数更大程度的可变性，它们对极端降水值比其它非极端降水更具有影响力（Nourani et al., 2020）。因此，本论文重点讨论τq与极端降水值的影响。在单体状（图4a）和块状（图4b）回波中强对流降水小波多尺度分解后分形参数τ1、τ2的比较中（图4c，d），计算出离散状回波分形参数τ1= 1.31、τ2=2.39，块状回波分形参数τ1=1.35、τ2=2.37，发现它们的分形参数差别不是很大。

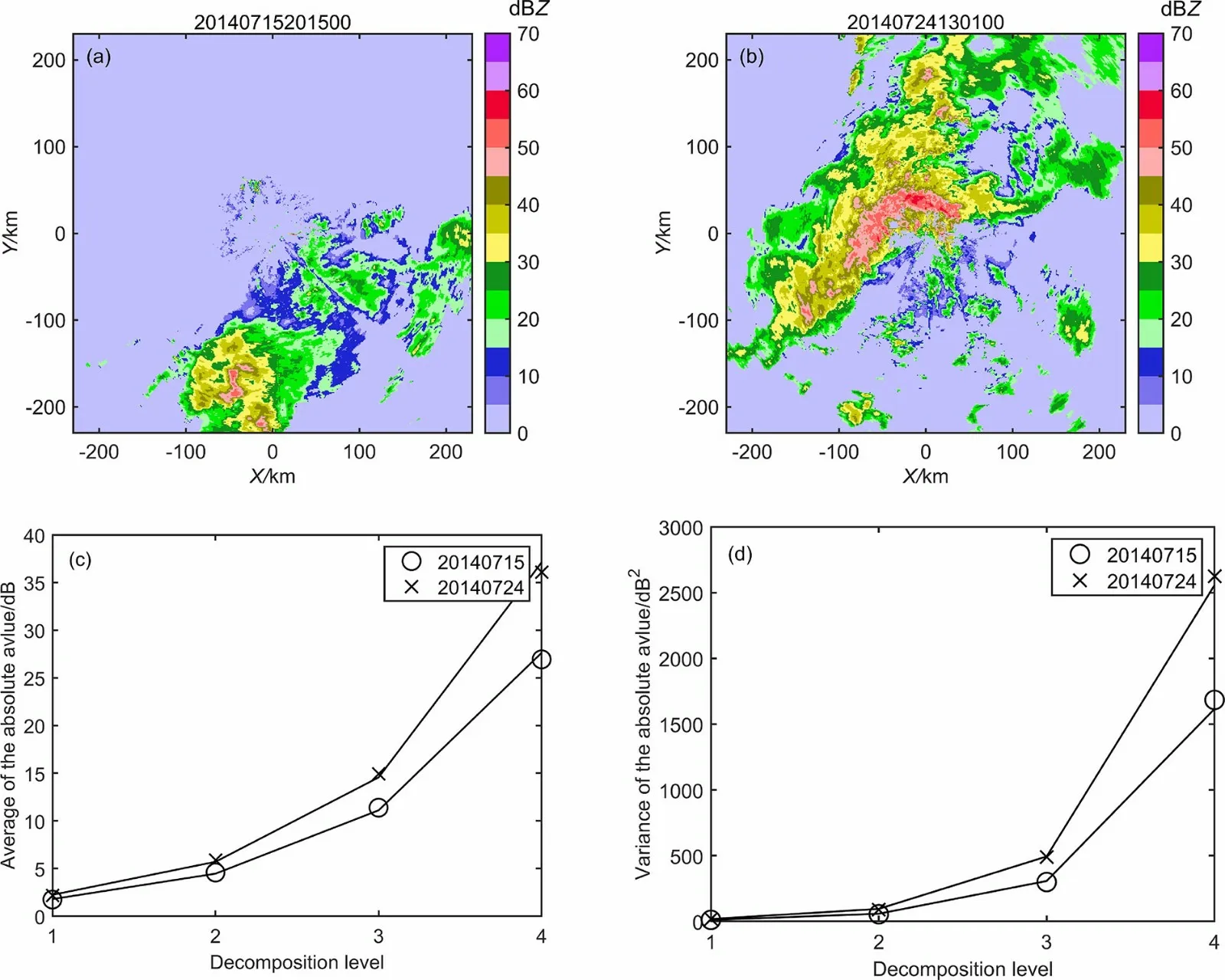
图4 （a）单体状（2014年7月15日20时15分）和（b）块状（2014年7月24日13时01分）强对流降水回波场，水平向子带小波系数（c）一阶矩（一阶矩改成绝对值的均值）和（d）二阶矩（二阶矩改成绝对值的方差）随尺度的变化关系。图（c）和（d）中20140715、20140724分别表示2014年7月15日20时15分时刻和2014年7月24日13时01分时刻Fig. 4 Heavy convective precipitation field of (a) monolithic (2015 UTC July 15, 2014) and (b) massive (1301 UTC July 24, 2014) echo, and the (c)average and (d) variance of the absolute value of the wavelet coefficient in the horizontal sub-band with scale. 20140715 and 20140724 respectively represent the time at 2015 UTC July 15, 2014 and at 1301 UTC July 24, 2014 in (c) and (d)

基于180次降水事件，对强降水回波场进行小波分解，计算并统计出分形参数的范围（τ1，H：1.08～1.37，V：1.09～1.37，D：1.03～1.35，τ2，H：2.05～2.48，V：2.08～2.48，D：2.07～2.46）。为讨论不同形状不同回波形态雷达强降水的分形参数相似性和差异性，以及对不同方向的敏感性，下文对2013～2016年强降水雷达回波进行分类统计。

针对180次强降水过程的雷达回波形状分四种类别（单体状、块状、离散状、线状），选出单体状81个、块状65个、离散状95个、线状22个，其中一次强降水过程可包含多种类型的雷达回波。表1列出了不同形态雷达回波强降水不同方向子带分形参数的变化范围，可以看出二阶分形参数相比较一阶变化范围大，也更敏感。对比几种类型回波的分形参数，发现它们相差不大，块状回波的分形参数相对更集中，而离散状回波的分形参数比其它类型的平均值更小。对于线性状回波，其线性强回波的取向可能导致水平向子带分形参数与垂直向子带的分形参数有较小的差异。不同类型的强降水雷达回波小波分解后分形参数总体相差不大，差距可忽略，或者说不同的回波形态并不是决定强对流降水小波域统计特征的关键因素。因此，后续的研究可对强降水统计特征参数进行统一建模。

表1 不同类型雷达回波其分形参数值的范围Table 1 The range of fractal parameters for different types of radar echoes

2.4 小波系数的非高斯分布重尾特性与分形参数的关系

不同的强降水数据的重尾及稀疏程度不同，多尺度分解小波系数随尺度的变化也不同。对于一次强对流降水过程来说，雷达探测到的回波类型及其降水区域可能随时变化，它们的统计特征也可能发生变化，这里讨论小波系数的非高斯分布重尾特性与分形参数的关联性。对2015年6月29日雷达探测到的一次雷暴天气过程进行分析，雷暴自中午11时31分开始至6月30日03时05分结束，整个过程一共产生150个数据。在中间时刻，强回波分布在雷达站北部，以离散状的强回波为主，其周围有较多的弱回波，并伴有少量的杂波（图5a）。图5b是降水场经小波分解后水平向子带分形参数与重尾性参数α的变化时序图（其它方向子带类似）。在这次降水中，两个参数的变化都相对稳定，在降水发展最为强烈的情况下，其重尾性特征明显，α最小，达到0.17，而分形参数达到最大，两者体现了成反比的发展关系。其物理解释可为，随着强降水的持续发展，其雷达回波就存在越来越多的奇异值，表现为区域大或小的强回波中心，降水与非降水边界分明，强回波与弱回波区分明显，即回波起伏变化复杂，则小波分解后表现出明显的小波系数分布的尖峰和重尾特性，离峰值较远的少量大值也有相当的出现概率，而对于分形参数而言，在对流最为强烈的情况下，雷达体现的回波边界和强中心特征清晰，小波系数在不同尺度之间的差异越大，导致分形参数的值就越大，所以两者成相反的关系，重尾性特征明显对应大的分形参数。值得注意的是，在其它个例的降水中，都存在这种情况。

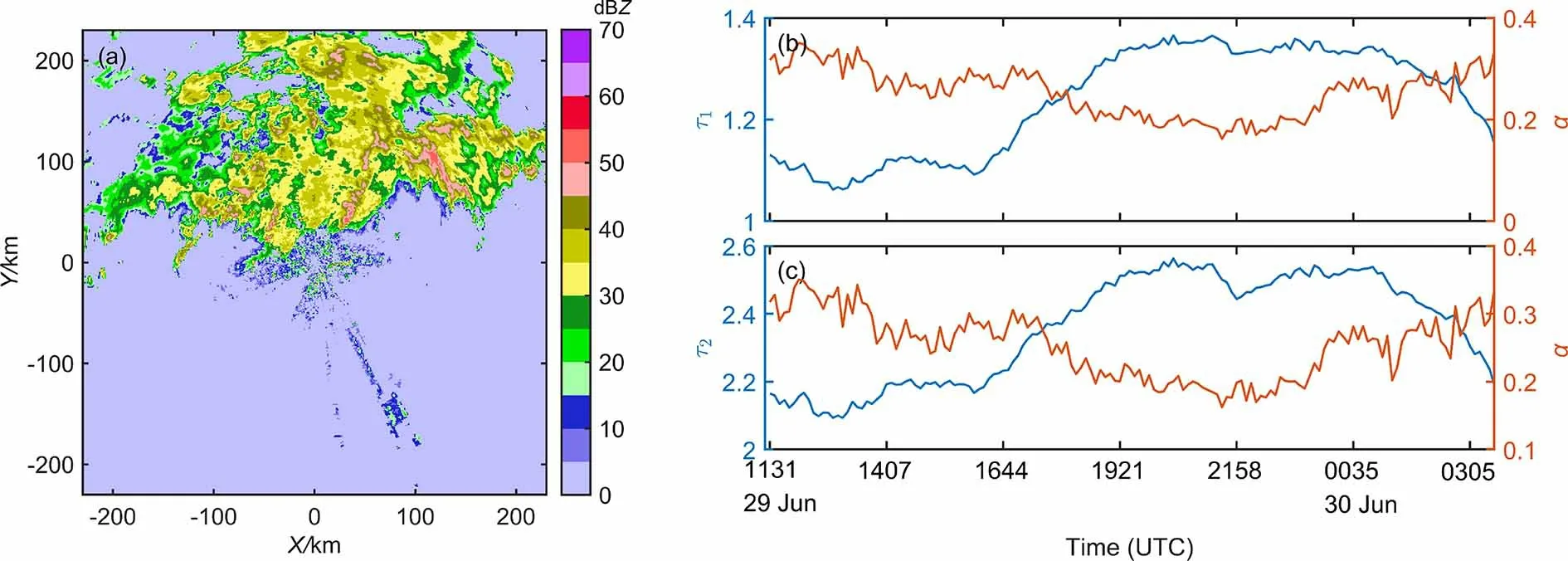
图5 2015年6月29日19时21分（a）南京降水个例回波强度，（b，c）此次强降水过程分形参数（一阶矩τ1、 二阶矩τ2）与重尾性参数α的时序变化Fig. 5 (a) Radar reflectivity image of the precipitation case in Nanjing at 1921 UTC June 29, 2015;sequence diagram of fractal parameters of (b) first moment τ1 and (c) second moment τ2 and heavy-tailed parameters α in the process of heavy precipitation

3 雷达强降水小波域统计特征参数与环境参数的关系

上文讨论了强降水的统计特征，发现一次强对流降水过程中分形参数与其重尾性特征参数成反比的关系，而统计特征的宏观特性都体现在强降水的雷达回波分布特征，表现为强对流的强雷达回波或者强回波的区域大小、位置，常用环境参数在气象预报中来表征强对流天气的强弱，由此联想到强降水小波域统计特征参数与强对流降水系统物理特征的相关性。而在气象学中，常常用各种参数来表征强对流的发生和发展，例如对流有效位能（CAPE）、K指数（K index）、对流抑制能（CIN）、总指数（TT）、每小时降水量（Total precipitation）、地表风速（Wind）等。所以，下文将利用多回归分析法讨论强降水小波域统计特征参数与环境参数的关联性。

因为常规气象站的探空资料所探测到的温压湿等气象要素的时间间隔是12 h，空间站点分布广，无法精确地捕获一次强对流天气过程的发生，所以本文采用欧洲中期天气预报中心（ECMWF）再分析数据ERA5的nc网格资料，该资料时间分辨率是1 h，空间分辨率为0.25°×0.25°。对上述180个降水事件进行筛选，选择雷达所能完整探测到对流发生发展过程的降水事件，针对此降水事件选出了93个强降水回波场，从反射率因子角度来看此回波场能够较好反映对流达到旺盛阶段，强回波与弱回波边际分明，降水分布均匀。然后进行雷达强降水回波场体扫数据与nc网格资料时间上匹配，选取雷达体扫数据事件与nc网格资料最相近时间。最后空间上选取相近时刻强回波中心区域所对应nc网格资料最邻近的区域进行匹配，以此得出nc网格资料各环境参数值。最终进行雷达数据小波分解后分形参数与nc网格资料各环境参数相关性统计。

图6是另一个强对流降水过程个例（南京地区，2015年8月7日），总过程历经约4小时，共有35个时刻雷达探测回波。一开始雷达站点的周围区域有大量离散状的单体生成，并伴有部分弱回波（图6a），经小波分解后其一阶分形参数值逐渐增大（二阶类似），而环境参数中的CAPE值、K指数在对流发生时也达到了最大值，最后随着对流的消失而减弱（图6b）。在此次对流过程中，对流抑制能（CIN）、总指数（TT）、地表10 m高度风速（WS）也存在相应的增减变化（图6c）。

图6 （a）2015 年 8 月 7 日 08 时 54 分南京降水个例回波强度，（b）此次强对流过程分形参数、（c）对流有效未能、（d）K指数、（f）对流抑制能、（g）总指数、（h）风速的时序变化Fig. 6 (a) Radar reflectivity image of the precipitation case in Nanjing at 0854 UTC August 7, 2015, and (b) the sequence diagrams of fractal parameter, (c) CAPE, (d) K index, (f) CIN, (g) TT and (h) WS （wind speed)

根据上述标准，图7a–h使用线性回归方法量化93个强对流降水场的分形参数与环境参数（CAPE、Total precipitation、CIN、WS）的关系，对于多数强对流降水来说，由于方向性并不明显，因此采用平均分形参数τ¯（水平向、垂直向、对角向子带分形参数的平均）来讨论。各环境参数中发现CAPE值与小波系数分形参数的平均值τ¯1相关系数为0.499，Total precipitation（每小时降水量）与分形参数的平均值τ¯1相关系数为0.3336，而其它环境参数与分形参数的相关系数低于0.28。其中，图7a、b分别为一阶矩分形参数τ¯1、二阶矩分形参数τ¯2与CAPE值的线(性回归图，)、的相关表达式分别为=0.0047CAPE×10−4+1.22和=0.0059(CAPE×10−4)+2.1212，都成正相关。表2列出了各个方向子带分形参数与各环境参数的相关系数。

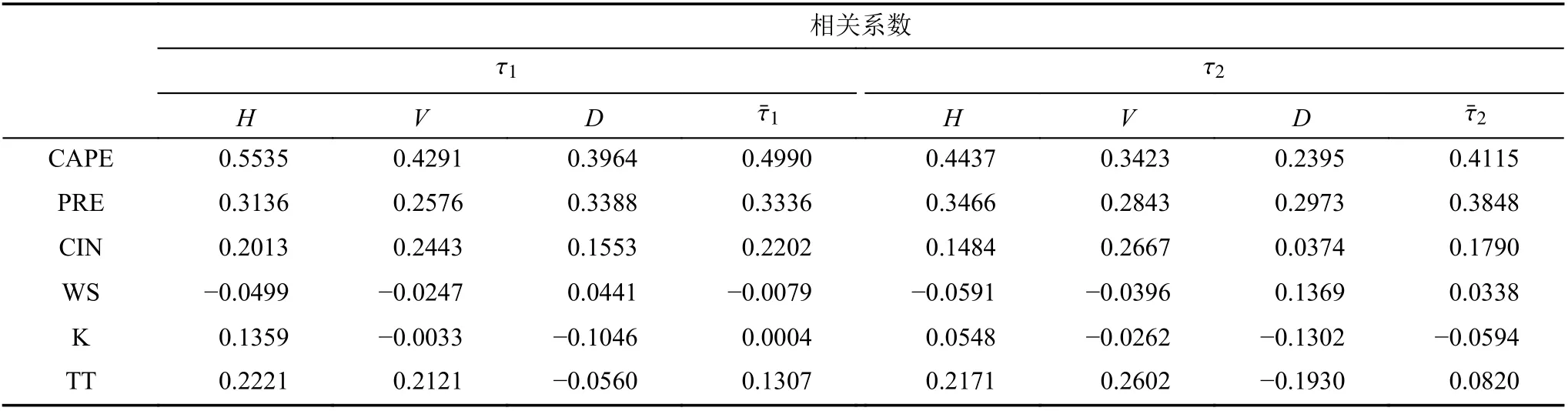
表2 各方向小波系数分形参数与各环境参数的相关系数表Table 2 Correlation coefficients of wavelet coefficient fractal parameters in various directions and various environmental parameters

强对流降水发生发展的时间短，移动速度快，可由单体或多单体演变而来，而CAPE体现的是大气中不稳定能量的大小，其值变化范围大，值越高对流的产生区域越可能导致高强度降水，一定程度上强的CAPE值与Total precipitation值相对应。图7中显示了CAPE对分形参数影响更大，较高的CAPE值或Total precipitation值对应较高的分形参数值，而分形参数表示相应小波系数的更大程度的可变性。而CIN和地表10 m高度风速（Wind）参数，其值变化范围小，在对流降水中无法很好地区分，且受下垫面的影响，不确定因素大，可能导致这些参数与分形参数相关性弱。

图7 强对流降水小波域分形参数（左栏：均值，右栏：方差）与环境参数的散点图Fig. 7 Scatter plot of heavy convective precipitation wavelet domain fractal parameters (left: mean, right: variance) and (a–h) environmental parameters

对流降水前的不稳定性越大，暴雨环境越动荡，体现在降水场空间变率的尺度变化就越大（Ebtehaj and Foufoula-Georgiou, 2011a）。分形参数与对流有效位能成正比关系，通常对于明显的强对流降水来说，降水区域分布面广，强回波区域也较大，而雷达回波在小波域表现出“尺度内相关性”和“尺度间依赖性”（寇蕾蕾等, 2019），邻域范围内的数据相关性较大，回波间梯度值相对较小，即降水波动变化较小，且在零均值附近，在多尺度分解过程中，随着分解级数增大，强降水的小波系数的增量高于弱降水，分形参数更大，通常高强度降水的分形参数比低强度降水明显。较高的CAPE值通常与较高的降水强度一致，分形参数与对流有效位能成正比关系。在中纬度中尺度对流系统中，建立的分形参数与环境参数的关系在次网格尺度降水参数化模型的建立中起着重要的作用，在数值天气预报中提供了更优的强降水变化特征。

4 结论和讨论

本文对南京市2013～2016年S波段天气雷达强降水回波数据进行小波域统计特征及其与环境参

数的关系研究，主要得出以下结论：

（1）强降水雷达回波场的小波系数的概率分布均呈现为大量小值和少量大值的构成形式，数值方差较大，即非高斯“重尾”特性，而这种重尾性反映了降水回波中的小尺度变化及一些强回波奇异值。而采用广义高斯函数来对小波系数的边缘进行建模，能够很好地解释强降水场小波域的重尾非高斯特征。

（2）天气雷达强降水数据回波的小波系数反映的是降水变化、边缘等细节信息，具有尺度间统计自相似性，表现出稳定的分形特征。对应一次雷暴天气过程中，从雷暴的发展至消散阶段，其分形参数的变化表现出连续性，且与重尾性参数成反比的关系，总体是一个先增加后减小的过程。不同形态回波强降水的分形参数相差并不大，方向性不明显。因此，利用不同类型的强降水雷达回波小波分解后分形参数差别不大，可为强降水小波域统计特征参数统一建模提供依据。

（3）在讨论强降水小波域统计特征参数与环境参数的关系中发现，一次强对流天气降水过程中，经小波分解后的降水场尺度系数随着环境参数的变化而产生相应的变化，随着对流的消失而减弱。使用线性回归方法分析分形参数与各环境参数的关系，发现环境参数中的对流有效位能与分形参数（τH：一阶水平向）正相关系数为0.5535、每小时降水量与分形参数（τ¯2：二阶各方向小波系数分形参数的平均）相关系数为0.3848，而其它环境参数与分形参数相关系数低于0.28。

本论文分析了强降水数据小波域统计特征以及与环境参数的关系，为强降水数据的精确先验建模提供较好的根据，从而更好地应用到多源降水数据融合或数据同化系统中，改进传统的基于线性的降尺度或基于高斯假定的同化方法，有效保持强降水重要的几何和统计特征。而对于强对流灾害性天气的检测与预报，合理地利用强对流降水小波域统计特征的先验信息，在后续的研究进一步分析极坐标下径向速度、不同地域、典型气候条件下的小波分解结果，并建立合适的次网格尺度降水参数化模型，不管在数值天气预报还是水文应用中都有着重要的参考意义。