基于ResNet 的智能恒虚警目标检测方法
张晨,叶舟,吕宇宙,方明,高永婵
(1.西安电子科技大学 电子工程学院,陕西 西安 710068;2.上海航天电子通讯设备研究所,上海 201109)
0 引言
由于能提高雷达在杂波、干扰背景下检测目标的能力,恒虚警检测技术一直是雷达信号处理理论和应用研究的基本问题之一。FINN等[1]提出了单元平均恒虚警检测(Cell Average-Constant False Alarm Ratio,CA-CFAR)算法,该算法通过计算邻近距离单元雷达杂波数据的统计平均值来估计待测单元的功率水平。CA-CFAR 检测算法要求待测单元的杂波与训练杂波数据满足独立同分布条件。然而,在实际雷达工作环境中,强杂波呈现出非均匀特性,沿距离单元的杂波统计特性差异变化较大,使得该算法的检测性能严重下降。
针对非均匀杂波环境给目标恒虚警检测带来的影响,国内外学者展开了大量研究[1-9]。TRUNK等[4]提出的单元平均选小恒虚警检测(Smallest of CFAR,SO-CFAR)算法和Hansen等[5]提出的单元平均选大恒虚警检测(Greatest of CFAR,GOCFAR)算法均首先计算待测单元两边的平均功率水平,再选取其中一个作为该单元的功率水平,但这两种算法无法兼顾目标检测性能和恒虚警特性。ROHLING等[6]提出了排序统计恒虚警检测(Order Statistic CFAR,OS-CFAR)算法,该算法首先将邻近单元的数据按升序排序,然后按照规则选择某一个单元的数值来表示待测单元功率水平。王永良等[8]提出了一种海杂波背景下的双参数有序统计恒虚警检测算法,该算法提高了在非均匀海杂波环境下的目标恒虚警检测性能,但同时带来了均匀杂波环境下检测性能下降和计算复杂度提高的问题。
作为一种高效的智能处理方法,深度学习能有效避免传统的复杂特征设计、具备较好的泛化能力[10-15],目前在视频处理领域、雷达图像处理领域等中取得了较好应用[16-18]。残差神经网络(Residual Neural Network,ResNet)[19-23]能解决随着网络加深而出现的梯度消失问题和退化问题,使网络在深层时具有更好的表达能力,具有挖掘杂波数据的高维数据特征和信息、实现雷达信号域智能处理的潜力。
因此,本文从杂波统计特征提取分类出发,提出了一种基于ResNet 的智能恒虚警目标检测方法。首先,根据雷达实测杂波数据建立雷达回波信号样本数据库、ResNet 的训练集和测试集;其次,构建ResNet 的智能提取杂波数据统计特征,并用该网络对测试集进行测试、实现分类;最后,根据分类结果实现基于ResNet 的智能恒虚警目标检测。
1 传统恒虚警检测方法及杂波特性分析
当雷达系统在接收K个距离维回波数据后{x1,x2,…,xK},需检测判决待检距离单元内是否存在目标。目标检测问题可描述为以下二元检测:

式中:假设H1为目标存在;H0为目标不存在;s为存在的目标;ci为第K个距离维的杂波数据。
经典的CA-CFAR 检测基本原理:首先,假设训练单元内杂波与待测单元内杂波满足独立同分布条件,选取M个训练单元和P个保护单元;其次,根据训练单元和保护单元的个数设置滑动窗口大小,取滑动窗口内单元的平均值与标称因子相乘得到阈值;最后,与检测单元进行比较,如果检测单元大于阈值则判断存在目标;反之,则判断不存在目标。
杂波幅度分布特性是杂波数据统计分析的重要部分,将其作为筛选杂波样本数据的准则,能解决实际检测中面临的样本不满足独立同分布的问题,从而提高恒虚警目标检测性能。
大量实测雷达数据分析表明,在实际工作环境中,杂波幅度的距离单元呈现不同的统计分布特性,典型的分布有瑞利分布、对数正态分布、韦布尔分布和K 分布。因此,区分不同幅度分布特性的杂波并建立服从相同分布的杂波样本数据子库是提高恒虚警目标检测性能的前提条件。
2 ResNet(RN)-CA-CFAR 算法
本文以ResNet18 作为杂波数据预分类的网络模型。ResNet18 是一种深度残差神经网络,共有20层结构,其残差块的结构如图1 所示。其卷积核大小为3×3,维度为64,激活函数为ReLU[21],且在2个残差块之间引入跳跃连接,保证反向传播更新参数时不会出现梯度消失问题。

图1 ResNet18 残差块结构Fig.1 Residual block structure of ResNet18
根据雷达实测杂波数据建立ResNet 的训练集和测试集,其中训练集由某雷达对海飞行收集的杂波数据组成,测试集数据为IPIX 雷达的海杂波测量试验中记录的杂波数据集子集。IPIX 雷达[24-25]是一个全相参的X 波段雷达,由其得到的高分辨率雷达数据已经成为测试雷达目标检测算法的重要基准数据。利用训练集数据对ResNet18 进行充分训练,并使用已有标签的测试集数据对已训练的神经网络进行性能测试,确保网络具备提取数据特征并实现准确分类的能力。
2.1 网络模型训练
根据已建的训练集,以雷达杂波数据构建ResNet,进行智能特征提取,得到杂波的统计特征。
利用海杂波雷达实测数据训练ResNet18,随机初始化网络的权重和偏置,通过随机梯度下降(Stochastic Gradient Descent,SGD)算法[22]和交叉熵损失函数逐步迭代更新网络的参数。网络的参数设置如下:分段函数初始网络学习率η0_seg为0.001,总迭代次数为100,类别数为4,批量大小(batchsize)为128。由于网络学习率η过大会导致网络不能收敛,η过小会降低网络优化的速度,因此本文分别采用分段函数和指数衰减函数Exponential LR 函数调整η,并比较2种η的调整函数对网络性能优化的影响。
Exponential LR 更新η为

式中:指数函数初始学习率η0_exp为0.05;g为底数,取值为0.7;e为训练的迭代次数。
η随迭代次数变化如图2 所示。

图2 η 变化曲线Fig.2 η curves
在保证其他超参数不变的情况下,将η分别设置为随迭代次数变化的分段函数和Exponential LR函数,η设置情况见表1。根据表1 和式(2)中η的设置情况充分训练网络,得到网络在训练过程中的损失函数值随训练次数变化如图3 所示。

表1 η 设置情况Tab.1 Setting of η
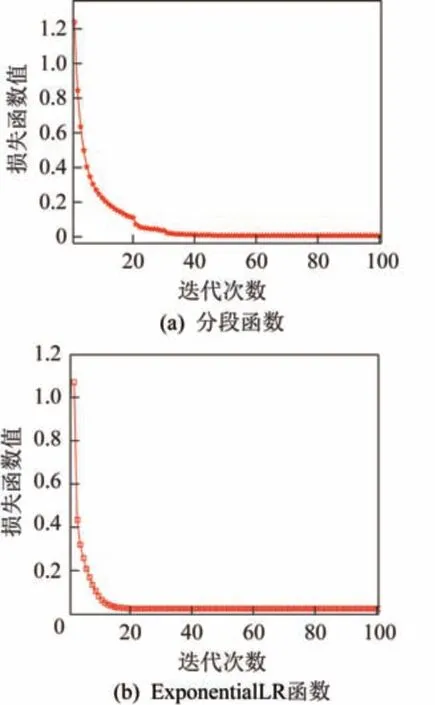
图3 损失函数值变化曲线Fig.3 Relationship between the iteration number and the loss function
由图3 可知,随着训练迭代次数的增加,网络的损失函数值逐渐减小。采用分段函数调整η的初始网络的损失函数值约为1.25,随着训练迭代次数的增加逐渐减少,最终近乎趋近于0。采用Exponential LR 函数调整η的初始网络的损失函数值约为1.1,随着训练迭代次数的增加逐渐减少,最终近乎趋近于0.02,这说明网络得到较充分的训练,网络性能得到优化。
批量大小对训练精度和网络收敛速度的影响很大,不同批量大小在测试集下的网络收敛情况曲线如图4(a)所示,不同批量大小在训练集下的网络收敛情况曲线如图4(b)所示。由图4 可知,随着批量大小的增大,网络分类准确率达到相同精度所需的迭代次数增多。但批量越大,每次迭代训练的数据就越多,当训练数据量很大时,增大批量大小可缩短整个训练过程的时间,且保证网络能够收敛。

图4 批量大小与损失函数关系曲线Fig.4 Relationship between the batchsize and the loss function
2.2 网络模型测试
基于所构建的ResNet,本节将对数据进行智能特征提取,得到杂波的统计特征,用训练好的网络对已知标签的测试集进行测试,并对统计特征进行分类,验证网络的泛化能力。
本节所用的测试集数据是IPIX 雷达的海杂波测量试验中记录的数据集子集。测试集数据与训练集数据由来自不同地点、不同时间的不同雷达采集所得。测试数据集共包含有400 个数据,其中杂波幅度特性满足K 分布、对数正态分布、瑞利分布以及韦布尔分布的数据各100 个。输入测试集数据,经训练的ResNet18 提取数据统计特征,再以阈值可设的Softmax 分类器对所得统计特征进行分类,根据测试集数据的真实分类和经网络得到的预测分类,分别记录4 种杂波幅度特性数据正确分类的数据个数,并计算4 种杂波幅度特性分类的准确率结果见表2。

表2 测试集分类准确率Tab.2 Test set classification accuracy
由表2 可知,分段函数调整η的ResNet18 经过充分训练能以较高的准确率实现杂波幅度特性分类,但服从韦布尔分布的杂波数据相比于服从K 分布、对数正态分布和瑞利分布的杂波数据较少。因此,网络关于服从韦布尔分布的杂波数据分类训练不充分,导致分类正确率较其他三类略低。经Exponential LR 函数调整η得到的分类准确率结果较为均匀,表明自动调整η的训练网络能在一定程度上降低训练样本数量较少对网络性能优化产生的影响。
实验结果表明:基于ResNet18 的杂波幅度特性分类算法效果优良,在后续的处理中可首先利用ResNet18 准确对杂波数据进行预分类处理,为剔除样本和建立杂波信号模型做了充分准备。
2.3 RN-CA-CFAR 检测
根据分类结果实现基于ResNet的智能恒虚警目标检测,RN-CA-CFAR检测器结构如图5所示。
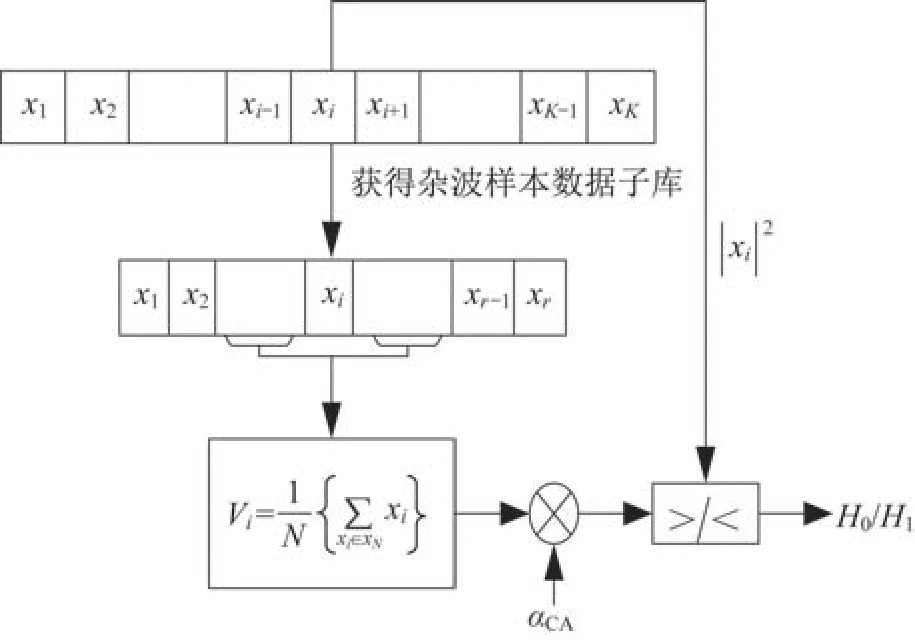
图5 RN-CA-CFAR 检测器结构Fig.5 Structure diagram of the RN-CA-CFAR detector
RN-CA-CFAR 检测的具体步骤如下:
步骤1根据分类结果建立不同幅度特性的杂波样本数据子库Xr,Xw,Xlog和XK;
步骤2根据待检单元xi(i=1,2,…,K,i为待检距离门的总数)服从的杂波幅度特性,在相应的杂波样本数据子库中选取与该待检单元临近的N个检测单元作为训练单元集XN;
步骤3计算待检单元的背景功率Pi=|xi|2;
步骤4计算训练单元集XN的平均值Vi=作为待检单元xi的背景功率水平;
步骤5利用门限因子计算门限TCA=αCAVi,其中αCA为根据所设定的虚警概率,αCA=,虚警概率Pfa和训练单元个数N确定的门限因子;
步骤6重复步骤2~步骤5,直到计算出所有K个待检单元的检测统计量为止;
步骤7根据自适应判决准则判定是否存在目标,自适应判决准则如下:

式中:H1为存在目标;H0为不存在目标。
根据以上过程,本文提出的RN-CA-CFAR 检测方法的算法总体实现框如图6 所示。

图6 RN-CA-CFAR 检测方法总体实现框Fig.6 Realization process of the RN-CA-CFAR detection method
3 实验结果及分析
本节所用数据是IPIX 雷达的海杂波测量试验中记录的数据集子集:总共包含34 个距离单元,每个距离单元的采样点数为60 000 个,每个实验使用全部距离单元的前12 544 个采样点,Pfa=10-6,训练单元个数N为6,试验参数为目标的信杂噪比(Signal Clutter Noise Radio,SCNR)。实验分为2组,该实验数据不含目标,因此在实验1 中插入2 个仿真目标,在实验2 中插入3 个仿真目标,目标信息见表3、表4。加入目标后的距离-脉冲如图7 所示。

图7 距离-脉冲回波Fig.7 Range-pulse echo pattern

表3 实验中各大目标的参数Tab.3 Parameters of each big target in Experiment 1 and 2

表4 实验中各小目标的参数Tab.4 Parameters of each small targets in Experiment 1 and 2
3.1 实验1 结果及分析
含2 个目标的回波数据分别在2 组不同SCNR下的恒虚警检测结果如图8 所示。

图8 存在2 个目标的恒虚警检测Fig.8 Schematic diagram of CFAR detection with 2 targets
其中,图8(a)的第6 个距离单元目标的SCNR为20 dB,第14 个距离单元目标的SCNR 为10 dB;图8(b)的第6 个距离单元目标的SCNR 为40 dB,第14 个距离单元目标的SCNR 为20 dB。
图8 为分别使用CA-CFAR、OS-CFAR 和RNCA-CFAR 检测器对回波数据进行目标检测的阈值曲线示意图。
由图8(b)可知,当目标具有较大的SCNR 时,由于目标功率较强,3 种检测器均表现出良好的检测性能;由图8(a)可知,当目标具有较小的SCNR时,CA-CFAR 检测器和OS-CFAR 检测器均不能有效检测第6 和14 个距离单元是否存在目标,而本文提出的RN-CA-CFAR 检测器则对目标具有较小的SCNR 表现出良好的检测性能。因此,本文提出的RN-CA-CFAR 检测器有效提高了在复杂海杂波背景下对弱小目标的检测性能,自适应能力更强。
3.2 实验2 结果及分析
含3 个目标的回波数据分别在两组不同SCNR下的恒虚警检测结果如图9 所示。
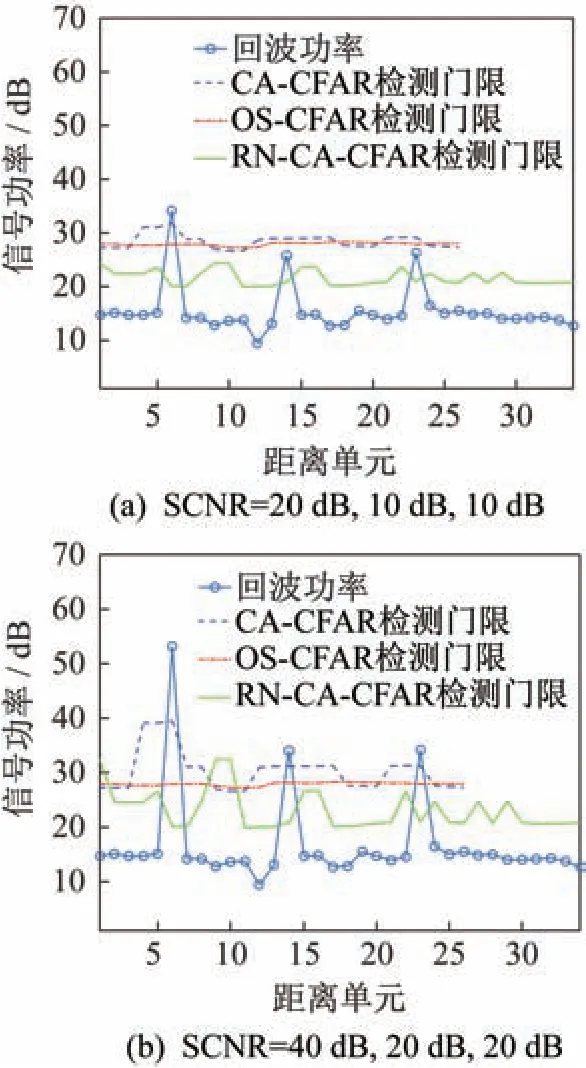
图9 存在3 个目标的恒虚警检测Fig.9 Schematic diagram of CFAR detection with 3 targets
其中:图9(a)的第6 个距离单元目标的SCNR为20 dB,第14 个距离单元目标的SCNR 为10 dB,第23 个距离单元目标的SCNR 为10 dB;图9(b)的第6 个距离单元目标的SCNR 为40 dB,第14 个距离单元目标的SCNR 为20 dB,第23 个距离单元目标的SCNR 为20 dB。
由图9(b)可知,对于目标功率较强的情况,3 种恒虚警检测器均能检测到目标信号,其中CACFAR 对20 dB 目标的检测性能较弱;由图9(a)可知,对于目标具有较小的SCNR=10 dB,CA-CFAR检测器和OS-CFAR 检测器不能在第16 个和第23个距离单元有效检测出是否存在目标,而本文提出的RN-CA-CFAR 检测器则表现出良好的检测性能。因此,本文提出的RN-CA-CFAR 检测器相比于传统恒虚警检测器性能更优。
4 结束语
由于观测环境、雷达平台以及雷达参数等因素影响,通常导致获取的雷达回波数据不满足独立同分布条件,使得传统恒虚警检测器性能不理想。针对该问题,本文提出了一种基于ResNet 的智能恒虚警目标检测方法。该方法通过雷达实测杂波数据构建ResNet 提取杂波统计特征,再通过测试数据进行分类,进而实现智能恒虚警目标检测。实验结果表明,相比传统恒虚警目标检测方法,本文方法具有以下优点:①引入深度学习思想,准确高效地完成了杂波数据分类和样本筛选,获得服从独立同分布的杂波训练数据;②自适应能力更强,在实际非均匀杂波环境下检测性能更好。

