基于动态编程匹配的聚类序列数据挖掘算法
曾 铮
(信阳职业技术学院 河南 信阳 464000)(中国农业大学 北京 100083)
0 引 言
随着大数据时代的来临,数据挖掘技术已经在金融、工业和运输等各个领域得到了广泛的应用与发展[1-2]。时空数据表示同时具备时间空间属性的数据,步入“互联网+”时代后,从巨大体量的时空数据中提取隐藏的巨大价值信息对于进一步充分挖掘数据潜力具有重大意义[3-4]。
时空数据挖掘方法主要包括时空频繁模式、时空共现模式和时空关联模式等,每种模式都有其各自的优缺点[5-7]。针对有两种或者多种同类型数据出现在间隔较短的时间或空间中的数据,比如天气数据、交通数据以及医疗数据等,时空共现模式由于其较强的时空关联性成为了该类数据挖掘研究的热点,但是绝大多数的研究无法直接从时、空两者出发进行数据挖掘[8]。针对该问题,李小红等[9]提出了一种共现聚类挖掘(Co-occurring cluster mining,CCM)算法,该算法包含两个评估函数,一个表示单个聚类在特征空间中的空间接近性,另一个表示聚类对之间的时间接近性。然而,由于模型简单性以及固定的标准,从而将序列分解成区间,忽略了共现事件的发生顺序和时间间隔。另外,该算法没有考虑多个事件发生内在联系,即未能充分挖掘事件相关性,从而限制了推理精度。
针对上述问题,提出了一种基于动态编程匹配(Dynamic programming matching,DPM)的聚类序列数据挖掘算法(Clustering sequence data mining algorithm,CSDM)。通过合成数据及燃料电池损伤分析实验证明了该方法在不确定情况下良好的推理精度。
1 聚类序列挖掘
1.1 相关定义
事件序列数据:将具有v维特征的N个数据点xk=(xk,1,xk,2,…,xk,v)∈D,k=1,2,…,N作为事件序列数据,其中数据点顺序为x1x2…xN,它们出现的时间表示为t(xk),则相应的定义式为:
针对事件序列数据挖掘必须满足以下要求:
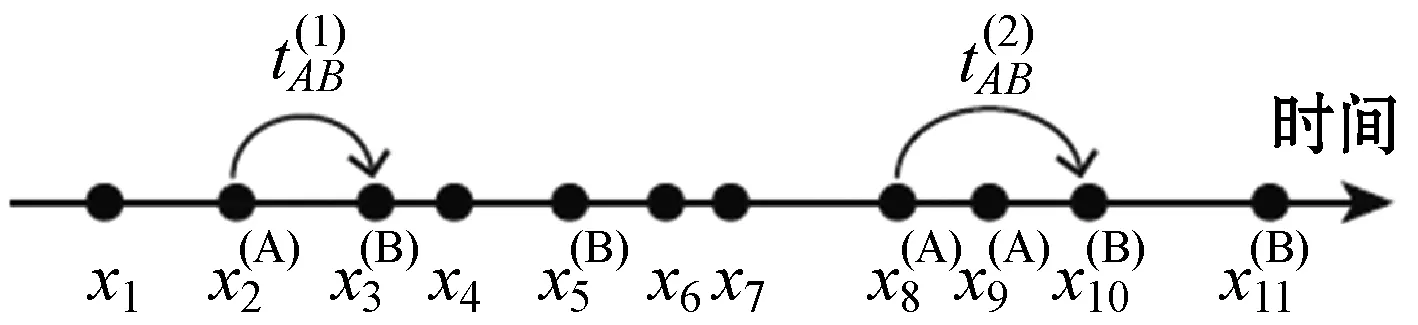
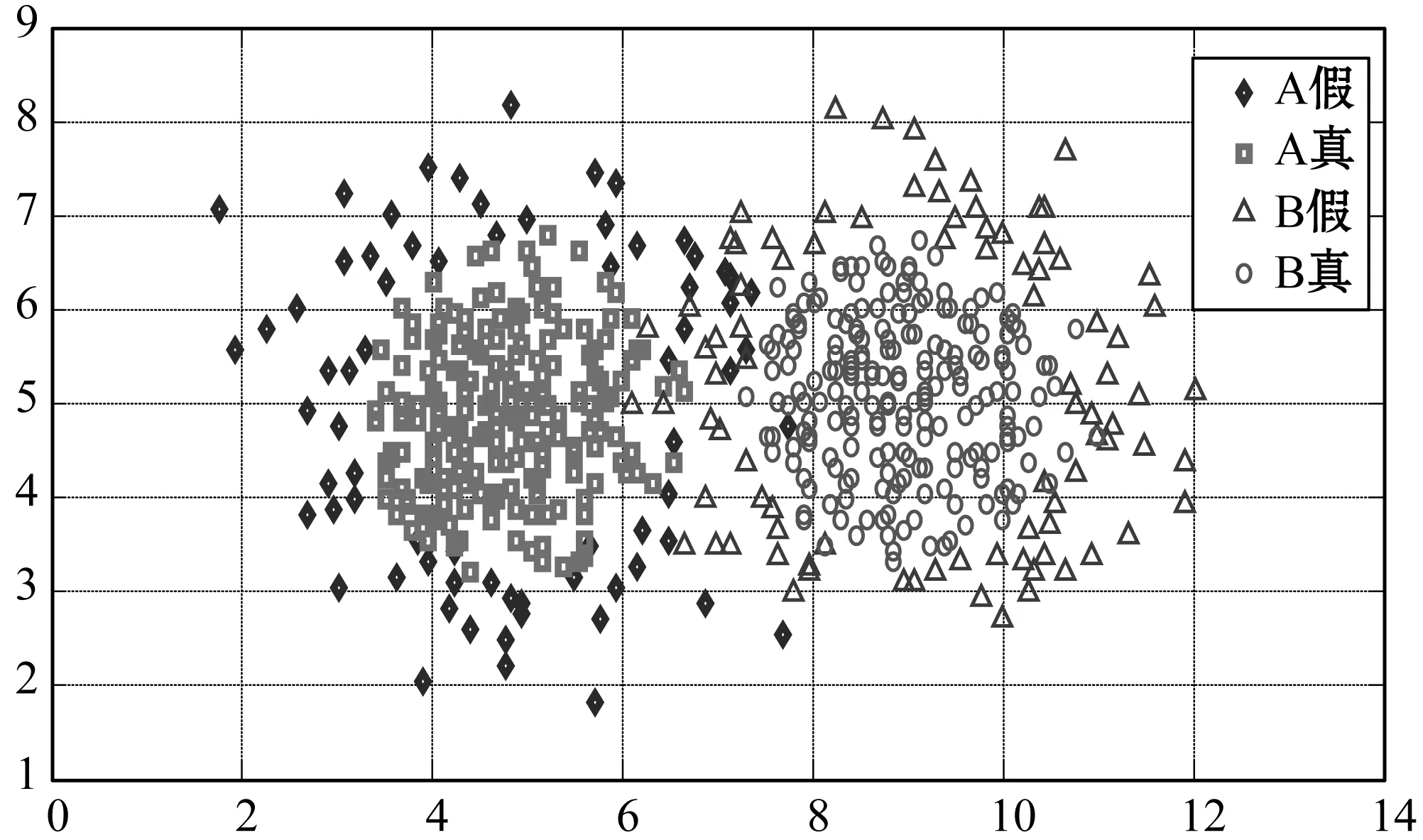
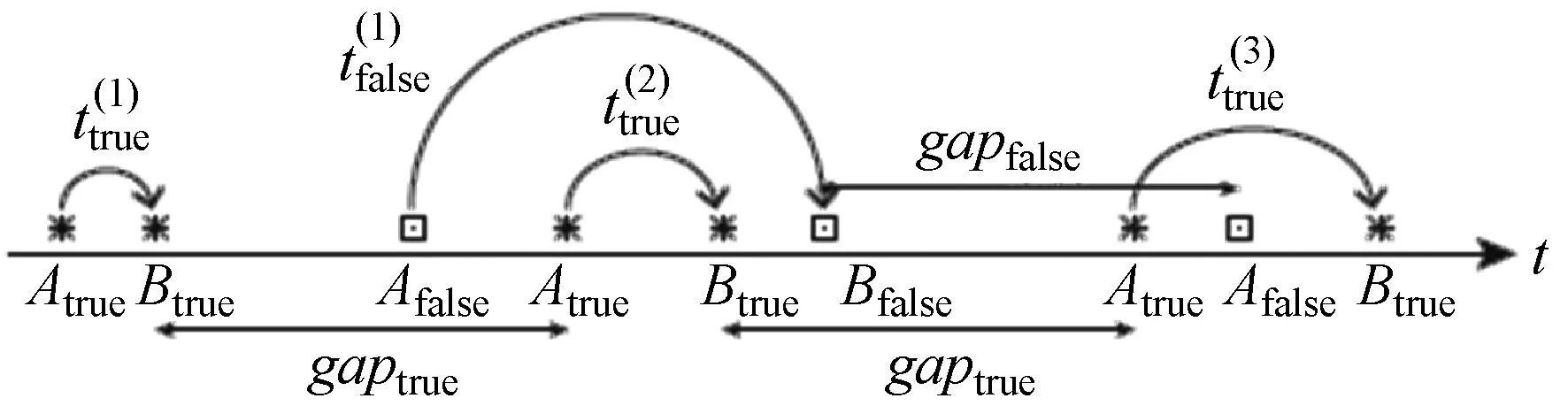
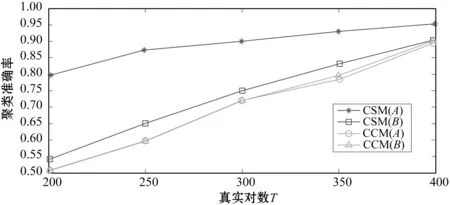
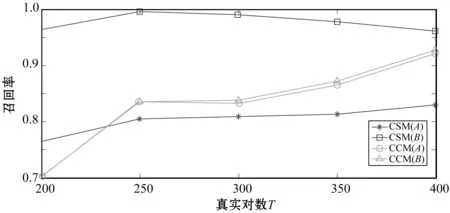
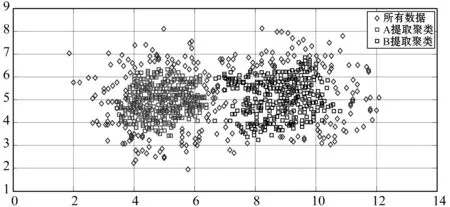
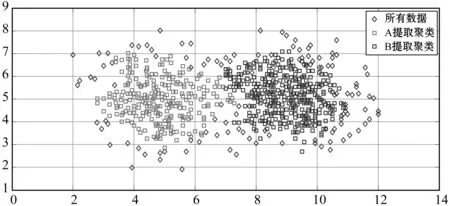
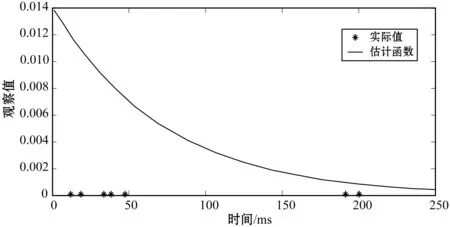
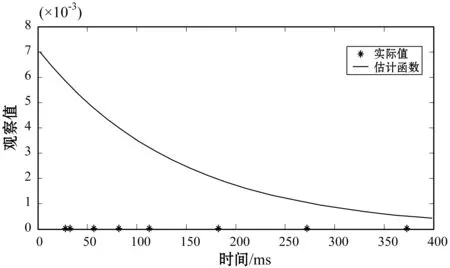
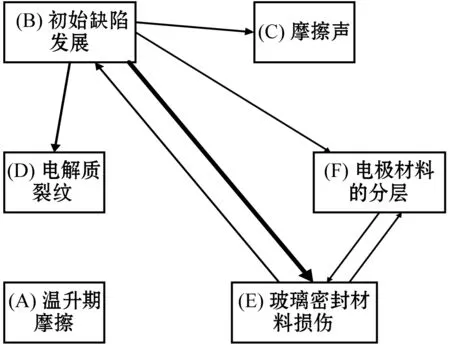
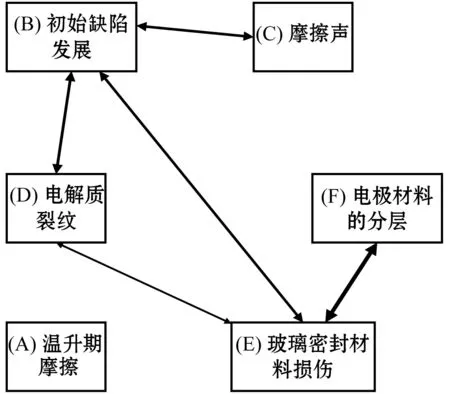
(1) 时间接近性要求:给定两个簇A,B⊂D(A∩B=∅),在事件x(A)∈A发生后,事件x(B)∈B几乎同时发生。即当存在实数Θ满足0 (2) 频率要求:如果x(A)∈A及其对应的事件对x(B)∈B出现的频率越高,则说明簇之间的相关关系就越强。因此,为了提供最小支持Suppmin,要求满足#{tAB}≥Suppmin,其中#{·}表示集合中元素数。 (3) 空间接近性要求:簇A(或簇B)中的事件在特征空间内紧密相邻。例如要求数据分布的簇内平方和(SSW)较小。其中,簇A和簇B可以独立评估。 (4) 聚类序列模式:假设事件x(A)和x(B)之间的所有对应的发生时间间隔的集合为: TAB={tAB|x(A)∈A,x(B)∈B} (2) 假定发生时间间隔概率密度函数(PDF)为: ψ(θ):tAB~ψ(θ) (3) 式中:θ为参数。事件发生时间间隔PDF满足上述三个要求的簇对A和B的集合可定义为: PA→B=〈A,B,ψ(θ)〉 (4) PA→B称为聚类序列模式,其中A可以称为先验聚类,B可以称为后验聚类。 CSDM算法包括生成和评估候选聚类序列模式的过程。有必要针对候选模式簇对A和B计算发生时间间隔集TAB。考虑两种事件的计算类型,分别为简单的一对一匹配和通过弹性匹配的多重匹配。 在此,以图1所示的事件序列为例,说明计算发生时间间隔的方法。事件x2、x8和x9属于簇A,x3、x5、x10和x11属于簇B,其余事件不属于任何簇。这是通过在特征空间中聚类来预先确定的。当事件以图1所示的顺序发生时,计算与任何A事件和B事件相对应的时间间隔。 图1 发生时间间隔的示意图 一对一匹配的计算算法如下,该过程在k=N的点完成[10]。 步骤1初始化计数器k=1并设置TAB=∅。 步骤4将时间间隔tAB=t(xpost)-t(xpre)添加到TAB。以k←k+1返回步骤2。 进一步考虑事件之间存在多重对应关系,为此设置了如下条件:(1) 一个事件可以配对多次;(2) 每个事件至少应配对一次;(3) 时间间隔的总和应最小化[11]。 其中,条件(1)和(2)用于尽可能多地增加生成的事件对的数量,以确保模式的可靠性。同时,在条件(3)中应将所有时间间隔的总时间最小化,因为根据本文中使用的时间接近的定义,较短的时间间隔表示它们之间的关系更强。 图2 计算时间间隔的多重匹配示意图 将上述条件公式化为多重匹配问题,如式(5)所示。 通常,事件发生的时间是随机的,具有极强的不确定性。假设时间间隔是根据以下指数分布发生的: ψ(tAB;λ)=λe-λtAB (6) 式中:λ>0是缩放参数;π(λ)表示参数λ的先验分布;ψ(tAB|λ)表示tAB的似然函数;并且π(λ|tAB)表示观察tAB时与λ相关的后验分布。根据贝叶斯定理得出: π(λ|tAB)∝ψ(tAB|λ)×π(λ) (7) 似然函数采用指数分布,因此先验分布获得伽马分布Γ(λ;α,β),其中α和β分别是形状和比例参数。先验分布参数αprior和βprior在没有特定目标的情况下,经常使用Γ(1,1)。后验分布参数可根据贝叶斯更新规则计算如下[12]: αpost=αprior+n (8) 定义候选聚类序列模式PA→B的评估函数为: 相反,函数G(A,B)是根据空间接近性要求评估函数。同样,G(A,B)值越大,空间接近度越高。SSW表示相对于簇中心的簇内数据点的分布。在此,使用σ>0的高斯函数作为用于调整候选模式之间的G值的相对分辨率的超参数,将值的范围归一化为[0,1]。用CCM的评估函数替换了F,而G与CCM中的相同[13]。 此外,L的评估函数定义为函数F和G的乘积;其中γ=0.5。提取模式时满足频率要求,其中相应的时间间隔数{tAB}大于或等于预先指定的最小支持Suppmin。 CSDM算法的运行步骤如下: 步骤1生成候选模式。首先,在数据空间中使用分层聚类生成候选聚类,而不使用时间信息。在排除包含关系之后,将所有可能的簇对都设置为候选模式集。 步骤2评估候选模式。根据函数L计算每个候选模式的评估值。当候选模式大于或等于预定义的最小阈值Lmin和Suppmin时,该模式将添加到输出模式集P。 步骤3排除重叠模式。最后,去除输出模式集P中的重叠模式,并使用其余的模式集,P(l)∩P(m)指Al∩Am和Bl∩Bm,P(l)∩P(m)≠∅表示两个模式都是具有包含关系的先验聚类或后验聚类时的情况。在这种情况下,采用具有较高L值的模式,而排除具有较低L值的模式。 合成数据是根据以下过程生成的: (1) 从分别以m1=(5,5)和m2=(9,5)为中心的两个不同的二维正态分布生成N个数据点,方差为1,协方差为0;每个数据点都表示为x~N(m,Σ),如图3所示。 图3 合成数据分布 (2) 从最接近各自正态分布中心的数据点创建了T个数据点对;每对包括先验聚类Atrue和后验聚类Btrue。其余数据点是代表噪声的错误数据,如图3所示。 图4 合成数据的示意图 在此实验中,总共生成了N=1 000个数据点,每个正态分布中有500个点。真实数据点的对数T是用于确定真实簇的大小和数据空间中周围噪声的比率的参数,而λtrue是用于确定时间接近的强度的参数,通过改变这些参数来评估CSDM。 当真实对数T发生变化时,对于簇C∈{A,B},根据式(13)-式(15)评估提取的模式PA→B的精度、召回率和F1度量三个参数来评估两种方法的聚类性能。 式中:Ctrue∈{Atrue,Btrue}是真实的聚类;而CCSM/CCM∈{ACSM/CCM,BCSM/CCM}是使用CSDM或CCM提取的聚类。当λtrue=0.05时,聚类结果如图5所示。数值越接近1,性能越好。由于此实验中只有一个真实模式,因此仅对CSDM衍生的具有最高L值的模式执行此评估。应用CSDM参数τ=100.0和σ=1.0,并将单链接方法用于层次聚类。由于合成数据是使用随机变量从正态分布和指数分布生成的,因此该图显示了30个实验的平均值。 P(A,B)),F1-measure(P(B,A))},则采用更好的F1度量。 图5(a)显示,对于先验聚类A,CSDM成功地以0.8或更高的准确率提取了聚类。图5(b)显示对于后验聚类B,无论噪声水平如何,CSDM的召回率均达到0.95或更高。当噪声较少时,即当存在更多真实对时,CSDM和CCM的F1度量之间没有主要差异。但是,图5(c)显示了CSDM成功地在噪声的情况下稳定地提取了聚类。另外,在真实数据的情况下,即不知道真实的聚类和对,CCM无法区分先验聚类和后验聚类。 (a) 聚类准确率 (b) 聚类召回率 (c) 聚类F1-度量图5 聚类结果 由CSDM和CCM提取的聚类的示例如图6所示。CSDM能够提取更接近真实聚类的聚类,而CCM提取的聚类包含比在真实聚类中可以观察到的更多的噪声数据。 (a) CSM方法提取结果 (b) CCM方法提取结果图6 从合成数据中提取的聚类 根据发生时间间隔估算指数分布的准确性是基于真实值的绝对误差: 表1 时间间隔分布的平均估计参数和误差Eλ以及标准偏差 此外,还比较了当改变合成数据的间隙参数gp时,CSDM在应用一对一匹配和DPM时的性能。平均值和标准偏差示于表2。一对一匹配对于较小的间隙(gp=1.0)更可能具有不正确的匹配顺序,从而导致较高的误差值,而DPM显示出较低的误差且不受间隙长度的影响。 表2 更改间隙参数gp时,CSDM中的一对一匹配和DPM的比较 表3 更改时间间隔参数λtrue时,F1度量的平均值和标准差以及时间间隔分布的估计参数 接下来,改变函数F和G的参数,并计算出聚类提取和指数分布参数的精度,如图7所示。在这种情况下,只有一个真实的模式具有相对较大的簇。因此,只要将预先指定的Lmin和Suppmin设置为合理的较低值,同一模式将始终具有最佳评估值。在实验中,这些值设置为Lmin=0.5和Suppmin=20。从图7可以看出,就簇F度量而言,τ和σ都有一个稳定的区域,一旦超过某个值,这两个参数的值就会突然变差。这说明聚类提取对τ和σ的变化不是很敏感。因此,可以将这些参数设置为稳定区域中的任何值。 (a) 参数τ的影响 (b) 参数σ的影响图7 超参数的影响(T=400,λtrue=0.05) 相反,时间间隔分布的误差Eλ对时间接近度F中的参数τ敏感,因此可以通过调整τ来显著改善。然而,实际上,应基于候选模式集中评估值的分布,从值的相对分辨率的角度进行调整,因为在使用实际数据集时不可能调整误差,因此真实值未知。另一方面,对于空间接近度函数G,参数τ在可接受的簇提取精度(F度量)的稳定范围内实际上是恒定的,并且对Eλ几乎没有影响。 由于燃料电池通过化学反应直接发电,因此已经开发了将其用作高效、低污染的下一代能量转换器的实际应用。在这些应用中,固态氧化物燃料电池(SOFCs)被认为是有效的大规模实现高效发电的手段。但是,由于SOFCs完全由固态陶瓷材料组成,因热和氧化还原膨胀而产生应力,这会导致电极或电解质中的裂纹和分层,并导致物理性能下降。为了描述这个问题,使用声频发射(AE)事件序列生成的内核自组织映射(SOM)对损伤过程进行可视化处理。另外,应用了CCM成功提取了材料之间的损伤共现关系。 SOFC中用于评估损伤的设备是在单电池中使用的标准材料组合物,其三氧化二铈基氧化物作为电解质,电极的横截面中央为三层结构,电解质夹在电极之间。单电池上方和下方是带有同心Al2O3管的气体环境(内径为8毫米,外径为13毫米)。在Al2O3管道之间放置一个屏蔽层,因此也使用熔化温度为800 ℃的苏打气环。 温度以200 ℃/h的速度升高到800 ℃,并在玻璃封口融化后保持1 h。然后以100 ℃/h的速度降低到550 ℃并在添加H2和O2气体的同时保持1.5 h。然后,温度以100 ℃/h的速率一次升高10 ℃,直到800 ℃,并保持1.5 h。然后以100 ℃/h的速度将温度降至20 ℃,并保持60 h。在此项实验中,损伤是由于突然降低温度而故意造成的。 使用宽带压电换能器(PAC UT-1000)以1 MHz的采样频率进行AE测量。换能器与电炉外部的Al2O3管道接触。来自换能器的电信号用40 dB的前置放大器放大,再用40 dB的主放大器放大。 首先,采用Kleinberg的猝发提取方法从连续测量的AE信号中提取AE事件,并获得1 429个AE事件。使用猝发提取方法,可以在不设置时间窗或幅度阈值的情况下提取任何长度的AE事件。接下来,通过应用傅里叶变换将每个获得的AE事件转换为频域,从而产生大约5 000个离散的功率谱点。 带有基于Kullback-Leibler散度的内核函数的内核自组织映射(Self organizing maps,SOM)将每个AE事件的离散功率谱用作输入数据x,以可视化二维平面上AE事件之间的相似性。SOM是一种无监督算法,主要用于聚类和可视化。根据先前的研究[18],可以通过直观地解释内核SOM结果来发现AE事件与损伤类型(例如电解质裂纹和电极分层)之间的大致对应关系。在这项研究中,CSDM被应用于内核SOM产生的可视化空间来解释事件。 由于内核SOM无法显式定义每个神经元节点的参考向量,因此它无法直接定义时间邻近函数G的集群内分散SSW。因此,根据以下公式代替式(12)重新定义G: 内核SOM中的神经元拓扑是2D方格,有15×15个神经元。如前所述,使用了基于完全链接方法的层次聚类。CSDM评估函数的两个超参数如第2节所述,τ=2.0和σ=0.5。此外,最小评价函数值Lmin被设定为0.7,最小支持阈值Suppmin=10。这些阈值影响提取的模式的总数和每个模式的置信度。结果从总共29个模式中获得了聚类序列模式。 考虑到物理现象以及与CCM提取结果的相似性,对CSDM提取的聚类序列模式进行了合理性评估。图8显示了CSDM提取的损伤模式的示例。在2D平面上以一种方式配置了内核SOM来说明各种模式,以便尽可能保留AE事件之间的相似性。每个单元格对应一个SOM神经元节点,相同颜色的相邻单元格表示由CSDM提取的单个聚类。图中箭头的方向指示先验和后验聚类的方向。此外,图8中(A)至(E)显示了先前描述的估计损害类型。图9显示了由CSDM估计的时间间隔的指数分布以及对于每种损伤模式的观察值。根据实际观察值,可以确认该趋势遵循在特定值处没有峰值的指数分布。 图8 CSDM提取的损伤模式的示例 (a) 损伤模式1 (b) 损伤模式2 (c) 损伤模式3图9 每种损伤模式的时间间隔 另外,图10描绘了其中将所有29个提取的模式分析为损伤类型之间的关系图,其中箭头边缘的宽度与模式出现的次数成正比。CSDM的提取结果如图10(a)所示,显示出与图10(b)所示的CCM相似的趋势。(B)和(C)以及(B)和(D)之间的顺序可以确定;相反,可以提取诸如(B)和(E)之间以及(E)和(F)之间的双向关系。 (a) CSM提取结果 (b) CCM提取结果图10 比较CSDM和CCM提取的模式 在图8所示的损伤模式1中,由于材料中的初始缺陷和不均匀而产生的裂纹(B)的发展导致产生电解质裂纹(D)的损伤模式。特别是,在图的上部中心区域中发生的AE事件表示损伤,尤其是在后期,由于材料的初始缺陷和不均匀性,裂纹频繁出现。可以认为当这些裂纹发展到一定程度时,在电解质中开始形成裂纹。 另外,损伤模式3是由玻璃密封损伤(E)和电极材料分层(F)引起的双向损伤模式。玻璃密封和电极材料在结构上没有连接,但是可以推测:当玻璃密封由于温度下降和电解质收缩而凝固时,在电解质和电极材料之间产生剪切应力,导致观察到的分层。相比之下,虽然玻璃中发生的塑性变形很小,但达到了突然出现裂纹的极限。综上,图10(a)表明了初始缺陷和玻璃密封材料具有显著影响。因此,通过解决这些问题,可以提高损伤分析的可靠性,并且分析得到的结论是符合先验知识的,进一步验证了方法的有效性。 针对共现聚类挖掘算法存在的局限性,本文提出了一种基于动态编程匹配的聚类序列数据挖掘算法。通过使用合成数据进行的实验,以及燃料电池损伤分析,可以得到如下结论:聚类序列挖掘算法即使在噪声不确定性相对较高的情况下,也可用于稳定地提取聚类序列模式。此外,动态编程匹配的引入可以有效地提高发生时间间隔概率密度函数估计的准确性以及推理精度。CSDM成功地确定了损伤模式的方向性,进一步证明了该算法能够应用于损伤模式判别。1.2 一对一匹配
1.3 动态编程匹配的多重对应
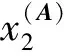
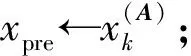

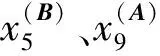


1.4 时间间隔推断概率密度函数
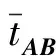
1.5 评估函数与计算步骤
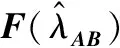
2 合成数据验证
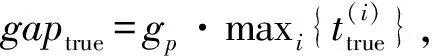
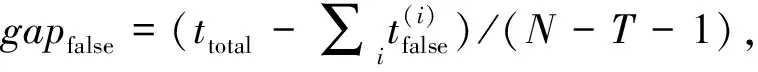



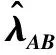

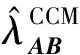


3 应用实例与分析


4 结 语

