基于改进噪声估计的MMSE-LSA语音增强算法

冯 谦 余 勤 雒瑞森* 黄天淏

1(四川大学电气工程学院 四川 成都 610041)2(桂林电子科技大学自动化学院 广西 桂林 541004)

0 引 言

噪声污染会使语音中的有用信息被湮没，严重影响语音质量和可懂度。语音增强技术[1]就是在尽量减少失真的前提下抑制噪声、改善语音质量的技术。目前的语音增强方法主要基于短时谱幅度估计法、语音参数模型法、听觉场景分析法等[2-3]。其中MMSE-LSA是基于统计特性的最优短时谱幅度估计器[4]，故本文采用MMSE-LSA谱估计算法进行进一步研究。

MMSE-LSA算法基于语音活动检测(Voice Activity Detection,VAD)[5]，利用语音和噪声统计特性的先验知识对带噪语音帧进行噪声帧和语音帧的判决，只在噪声帧来更新噪声估计，对语音帧则延续过去的噪声谱估计，再在最小均方误差准则下估计出谱增益函数，进而重构纯净语音。MMSE-LSA算法由于使用经验阈值来判决噪声帧和语音帧，存在较大误差，容易出现噪声过估计和欠估计，使增强语音失真和噪声残留问题严重。文献[6]引入了短时能量结合谱平坦度进行双门限判决的方法，对带噪语音段进行有无语音的划分，再在无语音段更新噪声估计，提高了噪声估计的准确性。文献[7]通过给增益函数添加约束条件，一定程度上解决谱增益过估计和欠估计引起的语音失真和噪声残留问题，进一步提高MMSE-LSA算法语音增强效果。文献[8]中MMSE-LSA谱估计器采用基于最小值控制递归平均(Minima Controlled Recursive Averaging,MCRA)算法，利用连续最小值跟踪得到初步噪声估计，再利用过去的噪声谱估计和当前帧的带噪语音功率谱的加权和作为当前帧的噪声估计，权重由先验信噪比或语音存在概率[9]决定。由于其语音存在概率由先验的语音存在和不存在的概率决定，仍然存在一定的噪声估计误差，使MMSE-LSA语音增强性能受限。文献[10]引入了短时能量和谱熵来组成能熵比，利用能熵比进行语音存在概率的估计，再结合谱减法进行语音增强，该方法能有效减小噪声估计误差，提高语音信噪比，但在非平稳环境下其仍然存在一定程度的噪声残留和语音失真问题。

针对以上情况，本文在文献[10]基础上提出一种基于改进噪声估计的MMSE-LSA语音增强算法。具体思想是：(1) 对带噪语音进行分帧、加窗处理，再对其做短时傅里叶变换，求出带噪语音的幅度谱和相角；(2) 计算出带噪语音的对数能量和谱熵，构建出新的语音特征参数能熵比；(3) 根据能熵比和语音存在概率的性质可知，能熵比和语音存在概率成正比关系，由此可以建立它们之间的数学关系模型，即可得到语音存在概率估计值；(4) 对估计出的语音存在概率进行平滑，利用平滑后的语音存在概率来更新噪声功率谱估计；(5) 计算出先验信噪比从而得到谱增益估计，再给增益函数添加一个约束阈值；(6) 利用MMSE-LSA谱估计器对带噪语音进行语音增强。本文采用多种常见噪声进行仿真实验，再使用真实广播信号进行验证，结果证明在多种噪声和复杂混噪环境下，本文算法能更准确地跟踪噪声变化，减少噪声残留和语音失真，改善语音质量。

1 MMSE-LSA谱估计器

假定y(n)是y(n)输入的带噪语音，s(n)s(n)是干净语音，d(n)d(n)是噪声信号，则带噪语音模型为：

y(n)=s(n)+d(n)

(1)

由于语音是非平稳信号，其在整个时域内是变化的，而我们认为其在短时内可看作性质平稳，因此在语音增强前通常需要先对带噪语音信号y(n)进行分帧、加窗等预处理，得到信号yi(m)，i表示第i帧。再对预处理后的yi(m)做短时傅里叶变换，得到第i帧带噪语音幅度谱Yi(ωk)和相位θy。由于干净语音的相位不好计算，利用人耳对相位不敏感的特点，可以直接用原始带噪语音的相位θy作为增强语音的相位估计，再通过反傅里叶变换可以得到增强后的语音信号，故我们只对纯净语音幅度谱进行估计。

假设噪声和语音相互独立，则可以对式(1)两边同时做短时傅里叶变换，得到：

Y(ωk)ejθy=S(ωk)ejθs+D(ωk)ejθd

(2)

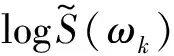
假设H0(ωk)和H1(ωk)分别表示语音不存在和语音存在两种状态，则概率密度函数分别为：

p(Y(ωk)|H0(ωk))=

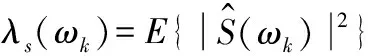
假设各个频率分量独立，基于上述最小化目标函数和概率密度函数，可最终得到优化的MMSE幅度谱估计器[11]：

式中：εk是先验信噪比，即第k个频谱分量的实际信噪比；γk为后验信噪比，即加入噪声后第k个频谱分量测量的信噪比。εk和γk数学表达式分别为：

Vk定义为：

由此可以对MMSE-LSA谱估计器的增益函数做如下定义：

至此，本文先采用改进的噪声估计方法估计出噪声功率谱，再由带噪语音功率谱和噪声功率谱估计求出后验信噪比γk，使用判决引导法[12]估计出先验信噪比εk：

式中：η是平滑系数，一般取0.98。

2 谱增益约束

MMSE-LSA算法谱增益的理想取值范围介于0到1之间。谱增益的过估计容易抵消掉弱语音，造成语音信息的丢失，谱增益的欠估计又会使噪声残留过量，影响语音信噪比。因此，本文通过给MMSE-LSA谱增益添加一个门限阈值来约束增益取值范围，约束谱增益如下：

式中：ε0为先验信噪比阈值；Gfloor为常数，通过实验取0.01。本文算法的整体框架如图1所示。

图1 本文算法整体框架

3 改进噪声估计

在非平稳环境下，MMSE-LSA算法存在较大的噪声跟踪时延，导致噪声估计值过高或过低。噪声估计值过高会造成带噪语音的过抵消，语音失真严重；噪声估计值过低会造成语音的噪声残留过多，影响人耳舒适度。因此，本文改进噪声估计方法，提高噪声估计的准确性。

3.1 噪声更新过程

本文算法的噪声估计基于时间递归平均的噪声功率谱估计思想，利用上一帧噪声功率谱估计与当前帧带噪语音功率谱的加权和来更新当前帧的噪声功率谱，其中噪声谱估计的平滑因子由语音存在概率来决定，具体表达式如下：

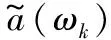
3.2 语音存在概率估计

能熵比是对数能量和谱熵的比值[13]，常被用于语音端点检测中，当其大于门限阈值，则将当前帧判为语音帧，反之则判为噪声帧。本文将利用能熵比进行语音端点检测延伸到估计语音存在概率上，由能熵比和语音存在概率的性质来建立能熵比与语音存在概率的关系模型，从而进行更准确的噪声更新。

3.2.1对数能量

语音段的短时能量通常明显大于无语音段，短时能量就是基于这一先验知识来对当前语音段进行判决，假设经分帧加窗后第i帧的带噪语音信号为yi(m)，则该帧的短时能量为：

式中：N为帧长。进一步改进能量计算[14]：

LE(i)=log10(1+E(i)/a)

(15)

式中：a是一个常数，能够使E(i)有剧烈波动时在LE(i)中得到缓和，适当选择a可以使纯噪声段和带噪语音段的区别更明显，本文中a取2.1。

3.2.2谱 熵

谱熵是用来描述语音平坦度的量，对有语音段，能量变化大，熵值越低；在无语音段，能量变化小，熵值越高。设含噪语音信号加窗分帧后的第i帧语音信号为yi(m)，经傅里叶变换后，设第k个频率分量的功率谱为Yi2(ωk)，则每个频率分量的归一化概率密度函数为：

则每个分析帧的谱熵[14]为：

3.2.3能熵比与语音存在概率的关系

由前面的分析可知，能熵比越高，语音存在概率越大；能熵比越低，语音存在概率越小。因此二者成正比关系。令Wi(ωk)为能熵比，则其表达式[13]为：

可将能熵比与语音存在概率的关系估计为：

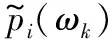
控制b取值不变，改变a的取值，得到能熵比与语音存在概率的关系曲线如图2所示，可以看出a取值越大，语音存在概率估计值随着能熵比增长越快，在能熵比足够大时语音存在概率估计值接近于1。

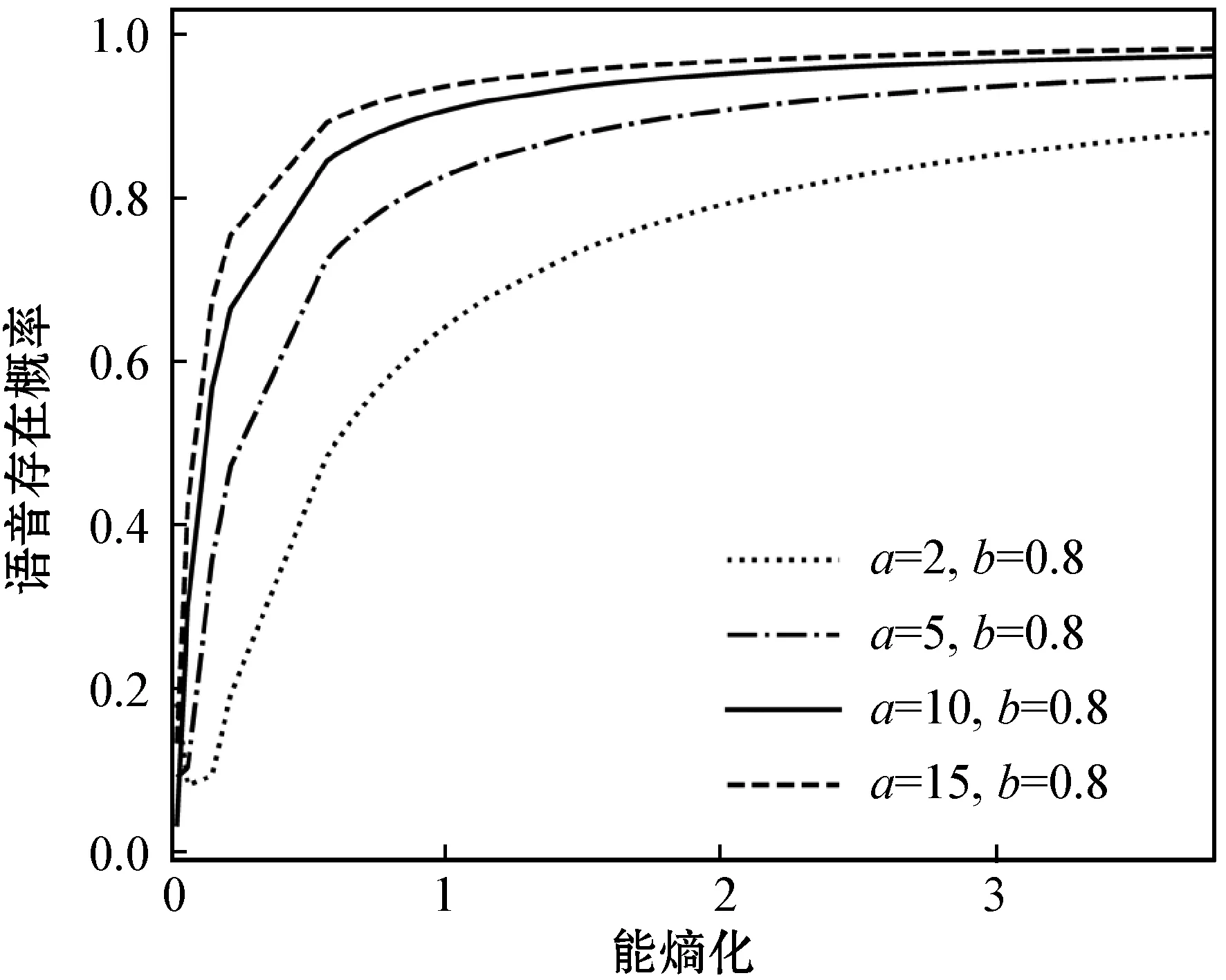
图2 能熵比与语音存在概率的关系曲线

最后对估计出的语音存在概率进行递归平滑，其平滑形式如下：

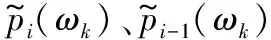
4 实验与分析

为了验证本文所提出的改进MMSE-LSA算法的性能，将传统MMSE-LSA算法、文献[8]基于最小值控制的递归平均算法、文献[10]基于改进语音存在概率估计的自适应噪声跟踪算法作为对比算法，分别使用TIMIT和NOISEX-92中的语料和噪声按不同的信噪比混合来模拟多种噪声环境，对比经每种算法处理后语音的信噪比、语音感知质量评估分数，同时结合语音波形进行比较，分析算法的增强效果。为验证本文算法对现实中复杂混噪语音的处理能力，采用广播信号进行实验，先对广播语音做语音增强，再使用项目已有的离线频谱管控系统来进行语音识别测试，对比各种算法处理后语音的识别率，可用来验证本文算法对解决实际语音增强问题的可行性。

4.1 仿真实验

从TIMIT语料库中选择5男5女共200条录音作为初始纯净语料，噪声源使用NOISEX-92数据库中的white噪声、babble噪声、F16和factory噪声。语音信号的采样率为16 kHz，帧长为512，帧间重叠50%，添加汉明窗。按-5 dB、0 dB、5 dB、10 dB这四种信噪比将噪声分别和每条纯净语音相加，得到200条含噪语音。

以平均输出信噪比SNR作为客观评价指标，语音感知质量评估(Perceptaul Evalution of Speech Quality,PESQ)作为主观评价指标，SNR表达式如下：

仿真实验中使用white噪声模拟平稳环境，其他噪声模拟非平稳环境，实验结果如表1所示。可以看出，不管是在平稳环境还是非平稳环境下，本文算法的输出信噪比SNR、PESQ分数表现都是最优，说明本文算法能较好地跟踪噪声变化，有效抑制噪声，改善语音质量，且能适应于多种噪声环境。

表1 输出信噪比SNR和PESQ分数

任选一条纯净语料，图3(a)为该条纯净语料的波形图，图3(b)为加入信噪比为5 dB的babble噪声后的带噪语音的波形图，图3(c)为经过文献[8]算法增强后的语音波形图，图3(d)为经过文献[10]算法增强后的语音波形图，图3(e)为经过本文算法增强后的语音波形图。可以看出，图3(c)残留噪声多，去噪能力有限；而图3(d)去噪能力强但会造成削波，导致语音音质受损；图3(e)显示本文算法具有较强的去噪能力，且能一定程度上抑制语音失真。

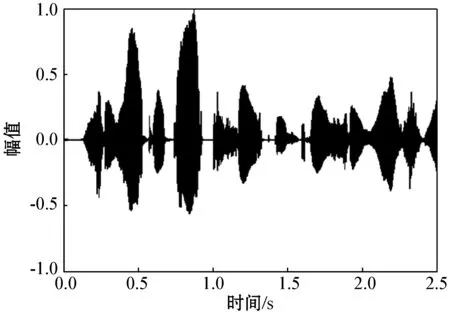
(a) 纯净语音

(b) 带噪语音

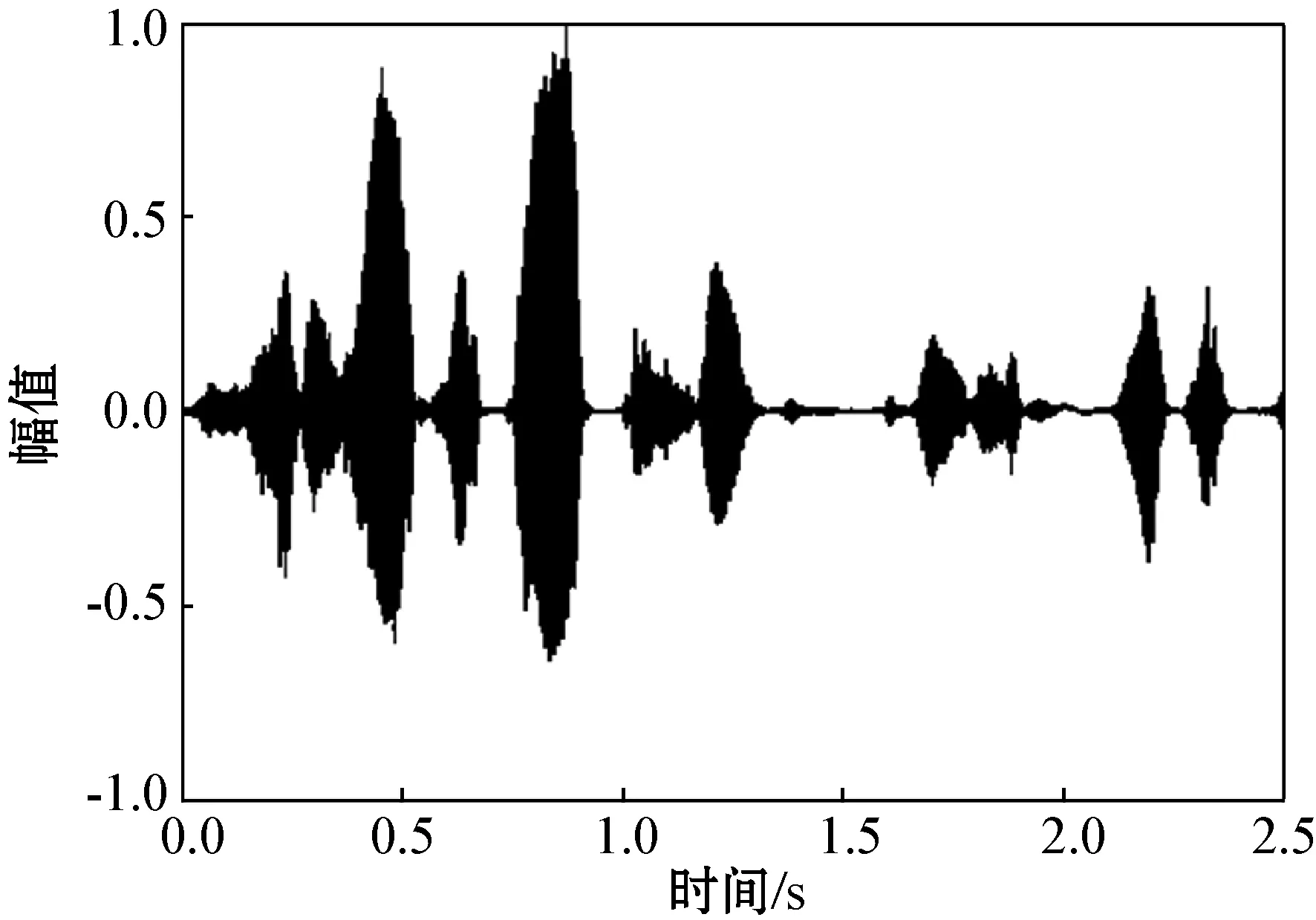
(d) 文献[10]算法

(e) 本文算法图3 各算法波形图

4.2 广播语音信号识别实验

为验证本文算法对真实混噪信号的增强性能，由于广播信号随机混有多种未知噪声、背景音复杂，适合作为实验对象。采用无线电信号接收器定点采集本地区某频段广播语音，切分成每条20 s以内的短音频，进行人工初筛分类后组成广播短语音数据集，采样率为16 kHz，16位量化。从数据集中随机抽取100条广播样本做语音增强处理，使用项目已有的离线频谱管控系统对增强前后的广播语音进行语音识别测试，以平均语音识别率[15]作为评价指标，图4为采用不同算法增强后的波形图对比，图5为语音识别率对比。

(a) 原始广播语音

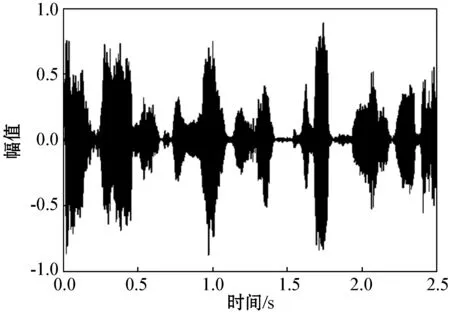
(b) 文献[10]算法

(c) 本文算法图4 不同算法增强后的波形图

图5 广播语音识别率

由图4可以看出，对真实广播语音信号，本文算法能有效抑制其背景噪声，改善语音质量，本文算法对处理现实环境中复杂混噪语音问题有一定参考价值。

由图5可以看出，原始广播语音的语音识别率为0.4左右，经过本文算法增强后语音识别率能达到0.78，提高了0.38，说明在处理复杂混噪语音时，本文算法能在抑制噪声的基础上较好地保留话语完整性，减少语音信息丢失，有效提高语音的可懂度。同时，从主观试听感受来说，增强前的广播信号背景嘈杂、有部分字词被噪声淹没，还伴随有随机尖峰声，而经语音增强处理后广播信号的人耳舒适度大大提高，特别是本文算法处理后音质有了明显改善，基本不影响对广播语音内容的理解。

5 结 语

本文针对MMSE-LSA算法对非平稳语音的噪声估计不够准确、导致语音增强性能受限的问题，引入能熵比参数来估计语音存在概率，再利用平滑后的语音存在概率来更新噪声估计；同时添加一个地板阈值来约束谱增益，缓解谱增益欠估计引起的语音失真。经多种噪声仿真实验和真实广播信号验证，本文算法能较好地跟踪噪声变化，减小噪声估计的误差，有效抑制噪声和减小语音失真，提高语音可懂度。