一类MIMO非线性系统的自适应神经网络鲁棒跟踪控制
刘德玉 邹坤霖 贺力克
1(湖南工业职业技术学院 湖南 长沙 410208)2(湖南大学机器人视觉感知与控制技术国家工程实训室 湖南 长沙 410082)
0 引 言
自适应鲁棒控制在控制领域的非线性系统中得到了广泛的关注。为了获得自适应和/或鲁棒性能,将许多先进的控制方法相融合来设计非线性系统的控制器。
由于具有非线性函数逼近、学习和容错能力,神经网络方法在非线性系统的建模和控制中得到了广泛的应用[1]。已经证明,多层神经网络可以尽可能精确地逼近任何连续函数[2-3]。基于其逼近性质,文献[4-9]提出了基于自适应神经网络的非线性控制方案,其中神经网络用于逼近单输入单输出(SISO)系统中的未知函数。随后,文献[10-12]扩展了自适应控制方案以控制多输入多输出(MIMO)非线性系统。在这些方案中,神经网络通常用于逼近系统的不确定非线性,从而为非线性系统设计补偿型自适应神经网络控制器;然后设计一个鲁棒补偿器消除逼近误差和外部干扰的影响,该补偿器可以是监督控制[13]、变结构控制[14]和/或H∞控制[15]。文献[11,14-15]利用神经网络完全逼近变结构的等效控制,然后应用H∞控制方法使闭环系统具有给定的跟踪性能。
本文针对一类不确定非线性MIMO系统,提出一种基于径向基函数(RBF)神经网络的自适应鲁棒反馈控制方案。控制方案包括RBF神经网络、滑模控制器和H∞最优控制器。利用RBF神经网络逼近非线性系统未知的理想反馈控制律,通过滑模控制器消除RBF神经网络重构误差和逼近误差。针对外部干扰,进行了H∞最优控制器的设计。采用二次稳定性方法,对参数不确定性进行独立处理,降低了传统鲁棒控制算法的保守性。基于李雅普诺夫稳定性定理,提出的智能鲁棒控制器能够保证闭环系统的稳定性和一定的跟踪性能。最后,通过质量-弹簧-阻尼系统的仿真实例验证了所提出控制方案的有效性。
1 问题描述
考虑由下面的微分方程表示的n阶非线性多输入多输出(MIMO)系统的广义形式:
x(n)=f(X)+g(X)u+d(t)
(1)
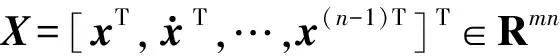
假设1未知非线性矩阵g(X)是有界的且非奇异的,即g-1(X)存在。

如果系统动力学是精确已知的,并且假设外部干扰被忽略,即函数f(X)和g(X)是完全已知的且d(t)=0,则理想反馈控制律可以设计为:
式中:xd是具有n阶可导的期望轨迹;e=xd-x是跟踪误差;系数k1,k2,…,kn应适当选择使得多项式h(s)=sn+knsn-1+k2s+k1的所有根都在s平面的左半平面内。
将式(2)代入式(1)可得到误差动态方程:
e(n)+kne(n-1)+…+k1e=0
(3)
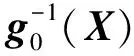
f(X)=f0(X)+Δf(X)
g(X)=g0(X)+Δg(X)
假设3假设标称函数g0(X)已知,其他函数和参数均未知。
假设3是合理的,因为一般情况下,非线性系统如机械系统或化学系统的控制矩阵g(X)相对容易获得可接受的精度;此外,g(X)的参数不确定性也已考虑。

2 基于RBFNN的自适应鲁棒反馈控制器设计
本文提出一种基于RBF神经网络的自适应鲁棒反馈控制方法,该方法由一个自适应RBF神经网络控制器和一个鲁棒混合补偿器组成,可以表示为:
u=un+uc
(4)
式中:un是RBF神经网络控制器;uc是混合补偿器。
由于f(X)和g(X)中包含的不确定性,式(2)是未知的,并且不能直接应用于式(1)。本文设计RBF神经网络来估计式(2)中的未知控制律u*,即:
un=ΘTΦ(xe)
(5)

定义RBF神经网络的逼近误差为:
ε(xe)=u*-Θ*TΦ(xe)
(7)
假设4假设存在一个函数κ(xe)>0,使得对于所有的1≤i≤m,有|εi(xe)|≤κ(xe)。
将式(4)和式(5)代入到式(1)中,可得:
g-1(X)[e(n)+kne(n-1)+…+k1e]=

定义跟踪误差的导数为:
式(9)对于时间的导数可以写成状态空间方程,其形式如下:
(10)
其中
且B=B0+ΔB。其中
假设5ΔB表示参数的不确定性,并具有以下结构:
ΔB=MFN
式中:M和N是具有适当维数的已知常数矩阵;F∈R2n×2n是未知Lebesgue可测矩阵。F边界为:
FTF≤I2n×2n
引理1设X、Y和F是具有适当维数的实矩阵且FTF≤I2n×2n。此外,对于任意标量α>0,
XFY+YTFTXT≤αXXT+α-1YTY
为达到一定的跟踪性能,式(4)中的补偿器uc可以设计为:
uc=uw+uh
(11)
式中:uw是消除RBFNN重构误差和逼近误差的滑模控制器;uh是H∞控制器,其任务是消除未知外部干扰的影响,同时实现特定的H∞跟踪性能。
对于基于RBF神经网络的自适应鲁棒反馈控制的设计,考虑采用式(4)所示的RBFNN控制器和鲁棒补偿器。假设存在一个矩阵P=PT>0,使得下面的不等式成立:
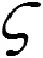
利用式(12)的矩阵P,选取自适应训练律为平滑投影[2]。考虑到当DΘ>0,δ>0时,有Ω0={Θ:ΘTΘ≤DΘ},ΩΘ={Θ:ΘTΘ≤DΘ+δ}。定义平滑投影映射:
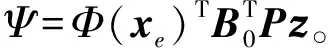
因此,RBF神经网络控制器的训练规律可以定义为:
式中:Γ是学习率。

uw=uwr+uwa
(15)
式中:uwr和uwa分别是消除RBFNN重构误差ε(xe)和逼近误差的滑模控制器。uwr和uwa定义为:
然后,混合控制器式(4)、式(5)、式(11)、式(15)-式(18)可以保证闭环系统的所有变量有界,并且可实现如下的H∞跟踪性能:

证明:定义Lyapunov函数为:
取Lyapunov函数对时间的导数,并代入式(10)和式(12),得:
(uwr-ε(xe))TBTPz+
考虑式(16)中的重构误差补偿器uwr和假设2,可以得到:
(uwr-ε(xe))TBTPz≤
-κ(xe)|BTPz|+|ε(xe)||BTPz|≤0
(22)
根据式(18)中的H∞控制器uh,将式(22)和式(23)代入式(21)中,可得:
根据假设5,有:

对式(25)从t=0到t=T进行积分,可以得到:
(26)
由于V(T)≥0,上述不等式导致了如下的L2准则:
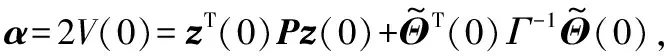
由于Q是正定矩阵,考虑λmin(Q)zTz≤zTQz可得:
(28)

(29)

3 仿真实验
本文将所提出的方法应用于控制质量-弹簧-阻尼器机械系统中,以验证所提出的智能鲁棒控制方法的有效性,如图1所示是一个质量-弹簧-阻尼器机械系统。质量-弹簧-阻尼器-机械系统的动力学方程可以表示为[11]:

定义:

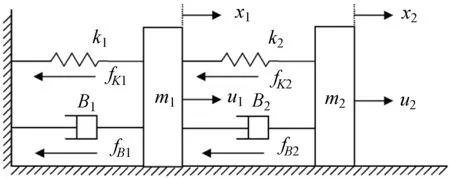
图1 质量-弹簧-阻尼器系统
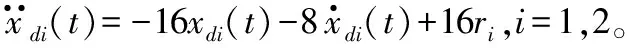
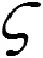

为了进行比较,将提出的自适应神经网络鲁棒二次镇定反馈控制(ANNRQSFC)方法与基于计算力矩方法(CTC)和文献[11]提出的神经网络鲁棒控制(NNRC)方法进行比较。文献[11]中所用的神经网络与本文所描述的结构相同。图2(a)和图2(b)分别给出了质量块1和质量块2的位置跟踪结果;图3(a)和图3(b)给出了位置跟踪误差;图4(a)和图4(b)分别给出了质量块1和质量块2的速度跟踪结果;图5(a)和图5(b)给出了速度跟踪误差。跟踪误差的均方误差(MSE)如表1所示。
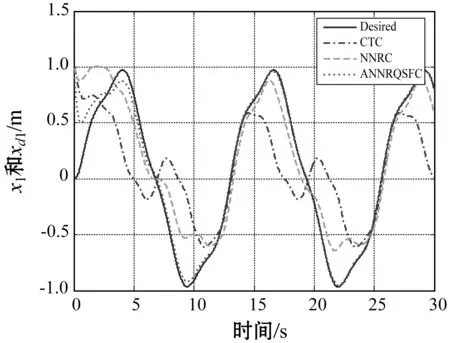
(a) 质量块1的位置跟踪
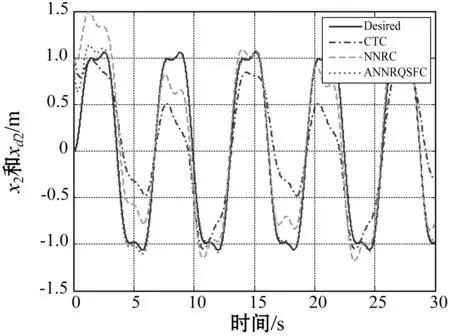
(b) 质量块2的位置跟踪图2 位置跟踪结果

(a) 质量块1的位置跟踪误差
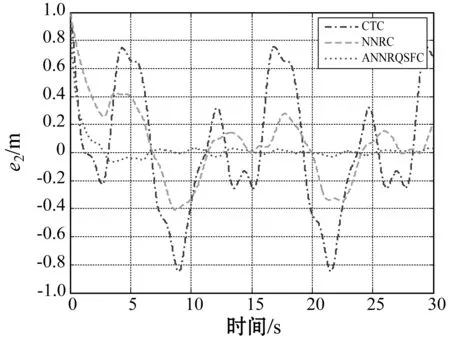
(b) 质量块2的位置跟踪误差图3 位置跟踪误差
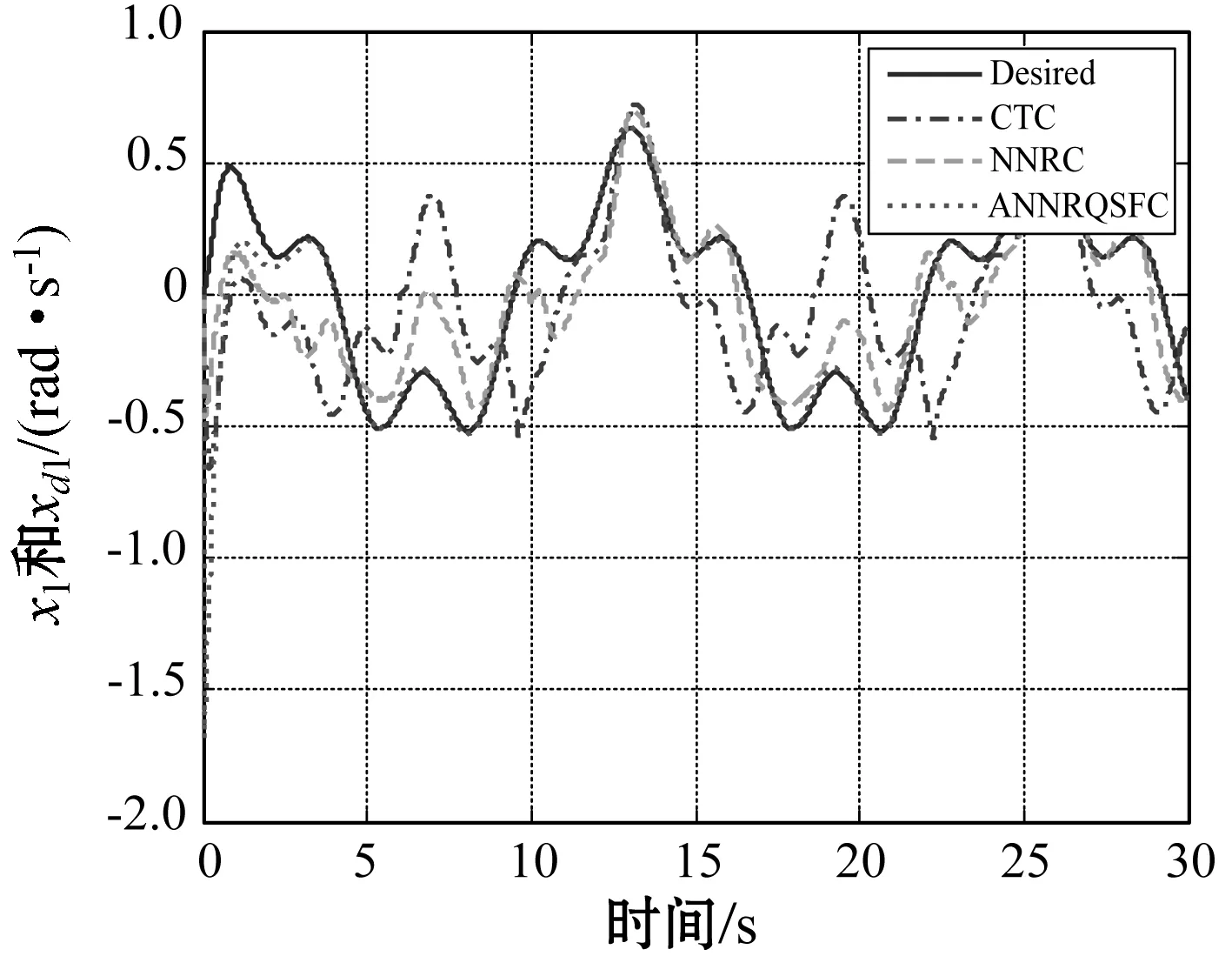
(a) 质量块1的速度跟踪

(b) 质量块2的速度跟踪图4 速度跟踪结果
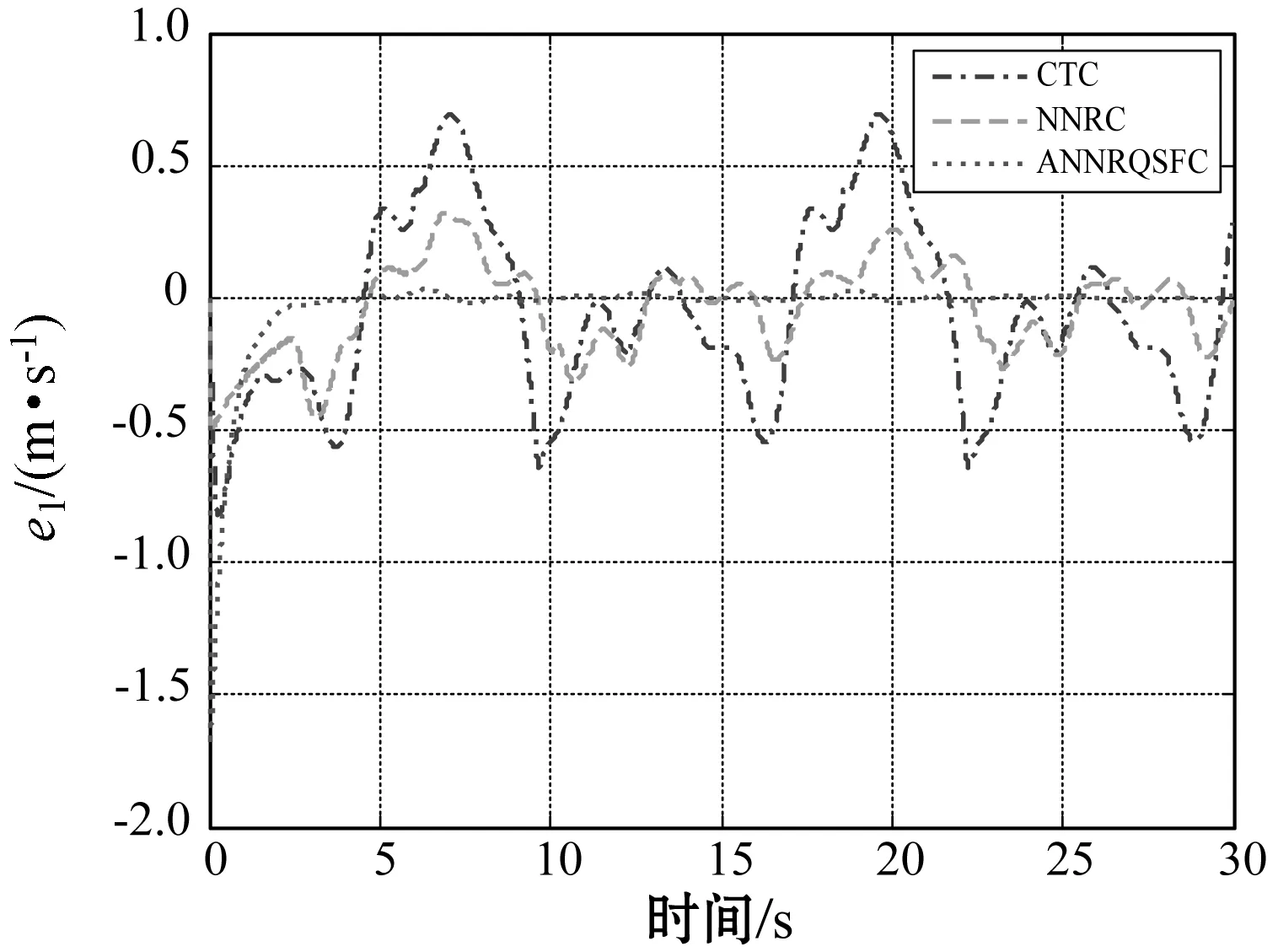
(a) 质量块1的速度跟踪误差

(b) 质量块2的速度跟踪误差图5 速度跟踪误差

表1 跟踪误差的均方误差 单位:m/s
根据图3(a)-图3(b)、图5(a)-图5(b)和表1,通过将所提出的控制方法与CTC和NNRC进行比较,可以看出由于CTC方法仅利用系统的标称值进行控制器设计,受系统中的不确定性和外界干扰的影响较大,跟踪效果也较差。NNRC和本文所提出的ANNRQSFC方法均采用神经网络对系统中的不确定性进行逼近,然后用鲁棒补偿项来消除神经网络逼近误差和外界干扰的影响,跟踪误差显著减小。而本文所提出的ANNRQSFC方法采用二次镇定方法,减小了鲁棒项设计时对于逼近误差和外界干扰上界的依赖,从而得到比NNRC方法更好的跟踪效果。图2-图5和表1也可以验证在存在不确定性和外界干扰的情况下,本文方法可以获得更好的性能。
4 结 语
针对具有不确定性和干扰的非线性MIMO系统,提出一种基于自适应神经网络的鲁棒反馈控制方案。该控制方法将神经网络与自适应鲁棒补偿器相结合,其中神经网络控制器作为主控制器,自适应鲁棒补偿器用于补偿神经网络的逼近误差和外部干扰。此外,采用二次镇定方法减小了传统鲁棒控制算法的保守性,实现闭环系统的稳定性和给定的跟踪性能。仿真结果表明,本文方法在具有不确定性的非线性系统的控制上表现出很好的鲁棒性和有效的控制性能,并具有良好的抗干扰能力。

