基于T-S 模糊模型的采样系统鲁棒耗散控制

练红海 肖伸平, 罗毅平 周笔锋

T-S (Takagi-Sugeno)模糊模型通过简单的IFTHEN 模糊规则,利用一系列的局部线性子系统结合模糊隶属度函数可精确描述非线性系统,广泛用于非线性系统的建模与控制,受到了国内外控制团队的极大关注[1-2].该模型结构简单,数学描述方便,有利于系统分析和控制器设计.因此,T-S 模糊模型系统的各种问题得到广泛研究[2-9],如H∞跟踪控制问题[6]、非脆弱滤波控制问题[7]、鲁棒耗散控制问题[8]、故障检测问题[9]等.

采样控制系统具有安装简单、可靠性高、维护成本低、效率高等优点而广泛应用于实际工程中.采样控制系统是一个包含连续时间信号x(t)和离散时间信号x(tk)的混杂系统,它的控制信号在任意一个采样间隔内只刷新一次(只在数据采样时刻刷新),与连续控制系统相比,这极大减少了信息的传输量,增加了带宽使用效率且控制更加高效.因此,采样控制系统得到众多学者的广泛研究,并取得了丰富的成果[10-19].文献[10-11]和文献[12]分别利用离散时间方法和脉冲模型方法研究了采样控制系统的稳定和镇定问题.文献[13] 提出了基于L-K(Lyapunov-Krasovskii)泛函的输入时滞方法,该方法是目前分析采样控制系统综合问题的主要方法之一,其基本思想是将采样控制系统转换为时变时滞系统,再利用L-K 泛函和时滞系统理论分析采样控制系综合问题.近些年,许多学者基于输入时滞方法提出了一些新的分析方法,如时间相关L-K 泛函方法[14]、闭环L-K 泛函方法[15]、不连续L-K 泛函方法[16-17]和双边闭环L-K 泛函方法[18-19]等.这些方法也已用于处理其他复杂系统的控制问题,文献[20]利用时间相关L-K 泛函方法研究了基于T-S 模糊模型的混沌采样控制系统指数镇定问题.文献[21]使用基于Wirtinger 不等式的不连续L-K 泛函和模糊比例采样控制分析了混沌系统的镇定控制问题.文献[22]利用基于自由矩阵的不连续L-K 泛函讨论了T-S模糊混沌采样控制系统的镇定控制问题.文献[23]通过双边闭环函数讨论了时变时滞神经网络的采样同步控制问题.

耗散性理论是Kalman-Yakubovich 引理,无源性理论以及圆判据的推广,它通过能量相关的输入输出描述方式给出了控制系统设计和分析的新框架,已成为非线性系统,鲁棒控制系统设计的重要工具.耗散性将无源性能和H∞性能进行了统一,为控制系统设计提供了一种更灵活,保守性更小的方法.另外,在耗散性能的基础上,还可引入扩展耗散性能[24],这个性能可将H∞性能、L2～L∞性能和无源性能纳入一个统一的框架.因此,研究各类动态系统的耗散控制问题具有重要意义.文献[25]针对具有随机扰动的模糊切换系统,讨论了其鲁棒耗散滤波控制问题并给出了滤波控制器的设计方法.文献[26]研究了时变时滞神经网络的耗散性问题,建立了确保系统严格耗散的充分条件.文献[27]分析了一类具有执行器故障的奇异Markovian 跳变系统的有限时间耗散控制问题.文献[28]研究了TS 模糊Markovian 跳变系统的可靠耗散控制问题.文献[29]研究具有执行器故障的T-S 模糊采样控制系统的可靠耗散控制问题.文献[30]针对一类TS 模糊采样控制系统,利用时间相关L-K 泛函方法研究了系统的鲁棒耗散控制问题,获得了系统严格耗散的充分条件并给出了模糊采样控制器的设计方案.由于它只考虑了采样间隔 [tk,t)的系统特征信息,忽视了采样间隔 [t,tk+1)的系统特征信息.因此,这种设计方法的保守性较大.考虑这种情况,文献[31]利用整个采样间隔 [tk,tk+1]的系统特征信息,提出一个双边闭环L-K 泛函,进一步研究了T-S模糊采样控制系统的耗散控制问题.虽然文献[31]的设计方案比文献[30]的设计方案保守性更小,但文献[31]没有考虑模糊前提变量,只是设计了一个线性的采样控制器,同时,它构造的双边闭环函数还忽视了一些有效的特征信息.因此还有很大的改进空间.

针对文献[30]和文献[31]存在的问题,本文进一步研究T-S 模糊采样控制系统的鲁棒耗散控制问题.主要贡献有以下几点:1)基于2 阶的B-L 不等式,提出基于B-L 不等式的双边时间相关不连续L-K 泛函,该泛函充分考虑了整个采样间隔[tk,tk+1)的特征信息和系统的不连续特性,相对现有的L-K泛函方法来说,可更加有效地捕获采样控制系统的锯齿结构特征;2)提出了一个改进的自由矩阵不等式,对L-K 泛函导数的估计更为精确;3)利用提出的L-K 泛函和自由矩阵不等式,建立了一个低保守性的鲁棒耗散性条件,基于这个条件,提出了T-S模糊采样控制器的设计方案.通过一个卡车拖车系统来验证设计方法的有效性和优越性.

本文采用如下记号:Rn,Rn×m分别表示实数域的n维向量空间和n×m矩阵空间; N 表示自然数集; 0 和I分别代表合适维数的零矩阵和单位矩阵;R ＞0 表示矩阵R是正定矩阵;Sym{M}=M+MT代表矩阵M与矩阵M转置之和; d iag{·}表示块对角矩阵;“*”表示对称矩阵的对称项;L2[0,+∞)表示平方可积无穷序列.

1 系统描述

针对一类连续非线性采样控制系统,考虑以下IF-THEN 模糊规则描述的T-S 模糊模型.

控制信号由零阶保持器(Zero-order holder,ZOH)输出产生.基于并行分布补偿控制 (Parallel distributed control,PDC)的思想,针对系统(1),给出下面的T-S 模糊采样状态反馈控制器.

采样周期为两个相邻连续采样时刻之间的间隔时间,假设满足

其中,h1和h2(h2≥h1≥0)分别表示采样周期(采样间隔)的最小值和最大值.

将式(4)代入式(2),可得下面的闭环采样控制系统

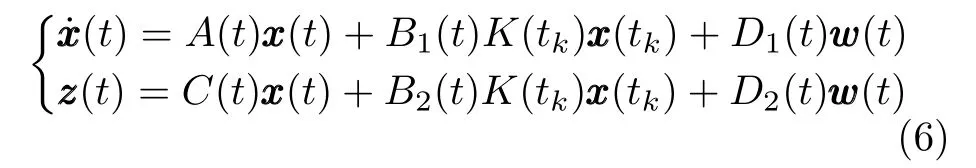
为了分析系统(6)的耗散性能,定义下面的能量供给率函数

则称系统(6)是严格(Q,S,R)-γ-耗散的.

本文目的是为系统(6)设计一个T-S 模糊采样控制器(4),且满足指定的耗散性能(8).

为了推导主要结论,给出下面两个引理.

引理 1 (2 阶B-L 不等式)[33-34].对给定矩阵R∈Rn×n,对所有在 [a,b]→Rn上连续可微的函数xxx,满足

引理 2 (改进的自由矩阵不等式).对给定矩阵R∈Rn×n,任意向量ξ0和自由权矩阵N,对所有在[a,b]→Rn上连续可微的函数x,满足

2 主要结果及证明

为了简化系统的分析与设计以及推导过程,定义如下标记符:

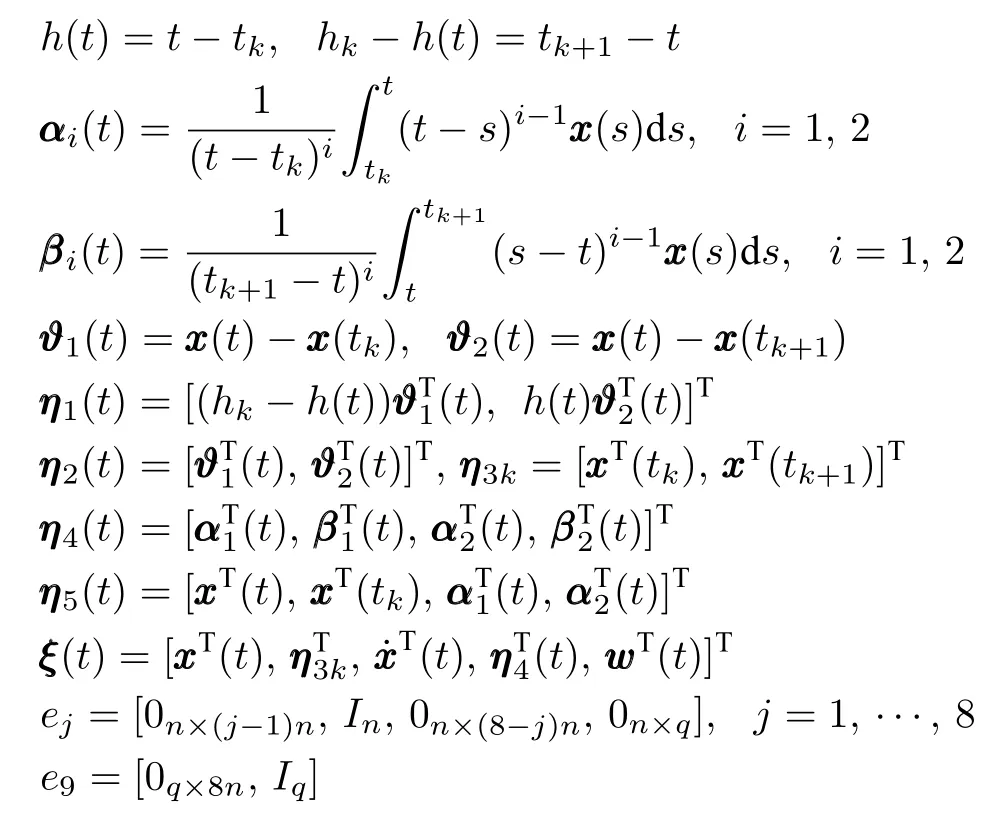
首先,对模糊采样控制器增益矩阵已知的情况,给出闭环采样控制系统(6)满足耗散性能(8)的充分条件如下.

其中,Σi,Ωi,i=1,2的定义见式(10)～(13).那么,系统 (6)是严格(Q,S,R)-γ-耗散的.

证明.构造基于B-L 不等式的双边时间相关不连续L-K 泛函为

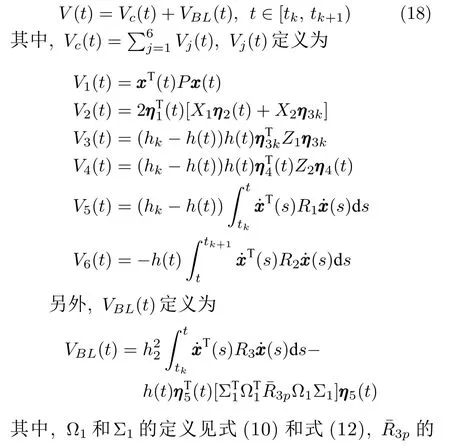
基于定理1,对控制器增益未知的情况,定理2给出了系统(6)鲁棒耗散控制的充分条件以及T-S模糊控制器的求解方法.

作为L-K 泛函,利用类似于定理2的证明过程,可得下面的推论

3 实例分析

本节提供一个实例来展示提出方法的可行性和有效性.考虑下面的卡车拖车模型[30,36],其卡车拖车模型示意图如图1 所示.

图1 卡车拖车模型及其坐标系统Fig.1 Truck trailer model and its coordinate system

其动力学状态方程可描述如下[30,36]

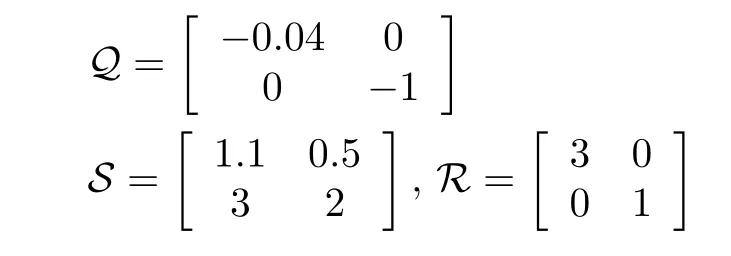
首先,针对变周期采样的情况(h12),选择ε1=0.7,ε1=0.5 和h1=0,对不同采样周期上界h2,使用定理2 和推论1 以及文献[30]所得的最优耗散性能指标γmax如表1 所示.由表1 可知,与文献[30]相比,定理2 和推论1 能提供一个更大的耗散性能指标γ.特别地,当h2=0.35 时,文献[30]无可行解,说明本文提出的方法更加有效.另外,从表1 还可看出,定理2 比推论1 提供的耗散性能指标γ更大,这是由于定理2 引入了VBL(t)和V4(t).

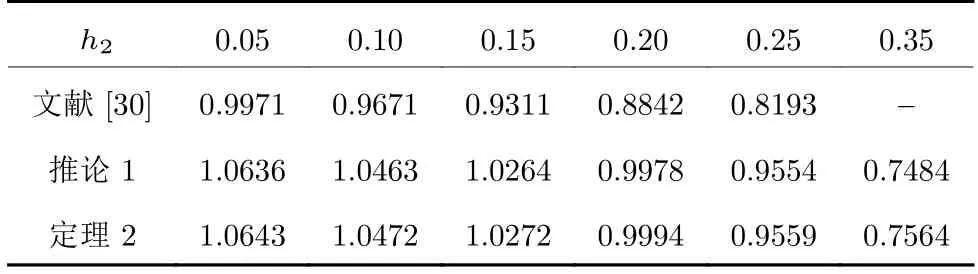
表1 对不同 h2的γmaxTable 1 γmax for differenth2

为了展示变采样周期下界h1与耗散性能指标的关系,选择h2=0.35,对不同h1,使用定理2 计算所得的最大耗散性能指标γmax如表2 所示,从表2可以看出,当变采样周期下界h1逐渐增大时,耗散性能指标γ也逐渐增加.

表2 对不同 h1的γmaxTable 2 γmax for differenth1

另外,选择耗散性能指标γ=0.9311 和变采样周期下界h1=0,使用定理2 计算所得变采样周期的最大上界h2为 0.26,与文献[30]所得结果 0.15 相比,结果改善了73.33%.此时,根据式(34)得到相应的T-S 模糊采样状态反馈控制器增益为

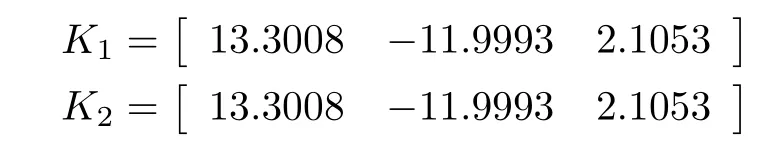
注 8.值得指出的是,目前大部分文献[20-22,29]获得的T-S 模糊控制器的各个局部子控制器增益是相等的(即K1=K2=···=Kr=K,r为模糊规则条数),根据,若各子控制器相等,则有uuu(t)=由此可知,全局控制器(uuu(t)=Kxxx(tk))与模糊隶属度函数无关.也就是说,当各局部子控制器相等时,得到的全局控制器(uuu(t)=Kxxx(tk))其实等价于一个线性控制器.关于局部子控制器出现都相等的情况,这可能与选择的隶属度函数,构造的L-K 泛函等多方面因素有关.对于这种情况目前尚没有统一的解决方法或合理的解释,是一个极具挑战性的课题,尚需进一步深入研究.

选择初始条件x(0)=[-0.5π,-0.75π,-10]T,外部扰动输入w(t)=[sin(0.1t)exp(-0.1t),sin(0.1t)×exp(-0.1t)]T.在γ=0.9311,变采样周期hk∈(0,0.26]情况下,基于获得的控制器,得到系统相应的状态响应曲线和控制输入曲线如图2 和图3 所示,从图2 和图3 可以看出,设计的T-S 模糊采样控制器保证了系统的稳定性,且能有效抑制外部扰动信号w(t),具有良好的鲁棒性.

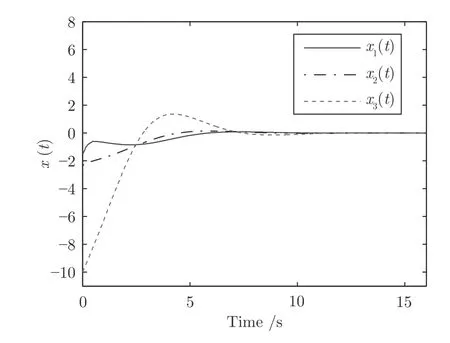
图2 变周期采样 h k∈(0, 0.26]的系统状态响应Fig.2 State response of system in the case of variable sampling withhk∈(0, 0.26]

图3 变周期采样 h k∈(0, 0.26]的系统控制输入Fig.3 Control input of system (38)in the case of variable sampling withhk∈(0, 0.26]

接下来,进一步讨论定周期采样的情况(h1=h2=h).对不同的采样周期上界h2,使用定理2 计算所得的最大耗散性能指标γmax见表3.由表1 和表3 可以看出,对相同的采样周期上界h2,定周期采样(h1=h2)的情况相比于变周期采样(h1h2)的情况来说,能获得更大的耗散性能指标.同时,从这两个表中,还可得出这样的结论:耗散性能指标越大对应的采样周期上界越小.换句话讲,可以通过增加采样频率来改善系统的耗散性能指标.

表3 对不同 h1=h2的γmaxTable 3 γmax for differenth1=h2

另外,选择耗散性能指标γ=0.9311,使用定理2 (h1=h2)计算得最大采样周期上界为 0.32,以及相应的T-S 模糊采样状态反馈控制器为

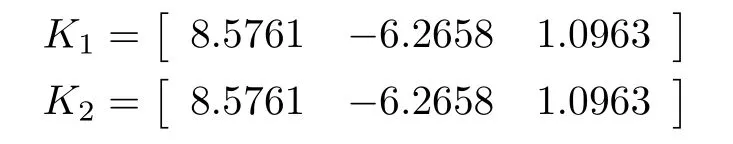
基于获得的控制器,可得系统的状态响应和控制输入如图4 和图5 所示.由图4 可以看出,设计的控制器能保持系统的稳定性,展示了提出方法的可行性和有效性.

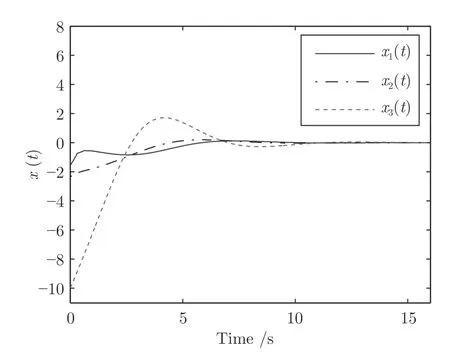
图4 定周期采样 h2=0.32的系统状态响应Fig.4 State response of system in the case of constant sampling withh2=0.32

图5 定周期采样 h2=0.32的系统控制输入Fig.5 Control input of system in the case of constant sampling withh2=0.32

4 结束语

针对基于T-S 模糊模型的采样控制系统鲁棒耗散控制问题.提出了一个基于B-L 不等式的双边时间相关不连续L-K 泛函.建立了一个确保系统严格(Q,S,R)-γ-耗散的充分条件.基于这个条件,提出了T-S 模糊采样控制器的设计方案.最后,使用一个卡车拖车系统说明提出方法的可行性和优越性,仿真结果表明所提出的设计方案能够实现良好的控制效果.

本文提出的方法也很容易扩展到其他复杂系统的分析与综合,如网络控制系统[5,37-38]、混沌系统[21-22]和神经网络[23]等,这将是我们进一步研究的方向.