多聚点子空间下的时空信息融合及其在行为识别中的应用

杨天金 侯振杰, 2 李兴 梁久祯 宦娟 郑纪翔

人体行为识别是计算机视觉领域和模式识别领 域的一个重要的分支,应用范围十分广泛,在智能监控、虚拟现实等应用中表现十分优秀[1-5].传统的人体行为识别使用的是彩色摄像机[6]生成的RGB图像序列,而RGB 图像受光照、背景、摄像器材的影响很大,识别稳定性较差.

随着技术的发展,特别是微软Kinect 体感设备的推出,基于图像序列的人体行为识别研究得到了进一步的发展.相比于彩色图像序列,深度图序列更有优势.不仅可以忽略光照和背景带来的影响,还可以提供深度信息,深度信息表示为在可视范围内目标与深度摄像机的距离.深度图序列相较于彩色图序列,提供了丰富的人体3D 信息,胡建芳等[7]详细描述了RGB-D 行为识别研究进展和展望.至今已经探索了多种基于深度图序列的表示方法,以Bobick等[8]的运动能量图(Motion energy images,MEI)、运动历史图(Motion history images,MHI)作为时空模板的人体行为识别的特征提取方法,提高了识别的稳健性;苏本跃等[9]采用函数型数据分析的行为识别方法;Anderson等[10]基于3 维Zernike的图像数据尝试行为分类,并且该分类对于具有低阶矩的行为是有效的;Wu等[11]基于3 维特征和隐马尔科夫模型对人体行为动作进行分类并加以识别;Wang等[12]从深度视频中提取随机占用模式(Random occupancy pattern,ROP)特征,并用稀疏编码技术进行重新编码;Zhang等[13]使用梯度信息和稀疏表达将深度和骨骼相结合,用于提高识别率;Zhang等[14]从深度序列中提取的动作运动历史图像(Sub-action motion history image,SMHI)和静态历史图像(Static history image,SHI);Liu等[15]利用深度序列和相应的骨架联合信息,采用深度学习的方法进行动作识别;Xu等[16]提出了深度图和骨骼融合的人体行为识别;Wang等[17-19]采用卷积神经网络进行人体行为识别；Yang等[20]提出了深度运动图(Depth motion maps,DMM),将深度帧投影到笛卡尔直角坐标平面上,生成主视图、俯视图、侧视图,得到三个2 维地图,在此基础上差分堆叠整个深度序列动作能量图生成DMM.DMM虽然展现出人体行为丰富的空间信息,但是无法记录人体行为的时序信息.针对现有深度序列特征图时序信息缺失的问题,本文提出了一种新的深度序列表征方式,即深度时空图(Depth space time maps,DSTM).

DMM 侧重于表征人体行为的空间信息,而DSTM 侧重于表征人体行为的时序信息.通过融合空间信息与时序信息进行人体行为识别,可以提高人体行为识别的鲁棒性,其中融合算法的可靠性直接影响了识别的精确度.在一些实际应用中,多模态数据虽然通过不同方式收集,但表达的是相同语义.通过分析多模态的数据,提取与融合有效特征,解决快速增长的数据量问题.常见的融合方法有子空间学习,例如Li等[21]将典型性相关分析(Canonical correlation analysis,CCA)应用于基于非对应区域匹配的人脸识别,使用CCA 来学习一个公共空间,测量两个非对应面部区域是否属于同一面部的可能性;Haghighat等[22]改进CCA 提出的判别相关分析(Discriminant correlation analysis,DCA);Rosipal等[23]将偏最小二乘法(Partial least squares,PLS)用于执行多模态人脸识别;Liu等[24]的字典学习(Dictionary learning method)广泛应用于多视图的人脸识别;Zhuang等[25]使用基于图的学习方法(Graph-based learning method)进行多模态的融合;Sharma等[26]将线性判别分析(Linear discriminant analysis,LDA)和边际Fisher 分析(Marginal Fisher analysis,MFA)扩展到它们的多视图对应物,即广义多视图LDA (Generalized multi-view LDA,GMLDA)和广义多视图MFA(Generalized multi-view MFA,GMMFA),并将它们应用于跨媒体检索问题;Wang等[27]对子空间学习进行改进,同样将它们应用于跨媒体的检索问题.本文提出多聚点子空间学习算法以用于融合空间信息与时序信息进行人体行为识别.

1 相关工作

1.1 深度序列特征图

1.1.1 运动能量图和运动历史图

Bobick等[8]通过对彩色序列中相邻帧进行图片差分,获得人体行为的区域,在此基础上进行二值化后生成二值的图像序列D(x,y,t),进一步获得二值特征图MEI,计算式为

其中,Eτ(x,y,t)为视频序列中t帧处的能量,由τ帧序列生成的MEI.

同时,Bobick等[8]在MEI的基础上,为了表示出行为的时序性,提出了MHI.在MHI 中像素亮度是该点处运动的时间历史函数.MHI 通过简单的替换和衰减运算获得,计算式为

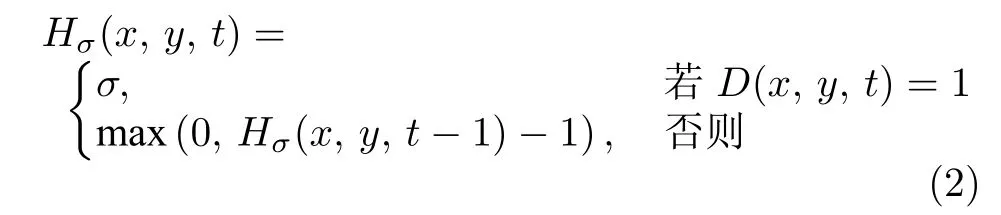
其中,Hσ(x,y,t)的初始像素亮度为σ,D(x,y,t)为整个图像序列.

1.1.2 深度运动图

Yang等[20]提出将深度序列中的深度帧投影到笛卡尔直角坐标平面,获取3D 结构和形状信息.在整个过程中提出了深度运动图(DMM)描述行为,每个深度帧在投影后获得主视图、侧视图和俯视图三个2 维投影图,表示为mapv.假设一个有N帧的深度图序列,DMMv特征计算式为

其中,i表示帧索引,表示第i帧深度帧在v方向上的投影,f表示主视图,s表示侧视图,t表示俯视图.

1.2 典型性相关分析

子空间学习的本质是庞大的数据集样本背后最质朴的特征选择与降维.子空间学习的基础是Harold Hotelling 提出的典型性相关分析(CCA)[15],CCA的主要思想是在两组随机变量中选取若干个有代表性的综合指标(变量的线性组合),这些指标的相关关系来表示原来的两组变量的相关关系.假设有两组数据样本X和Y,其中X为x1×m的样本矩阵,Y为x2×m的样本矩阵,对X,Y做标准化后CCA的计算式为

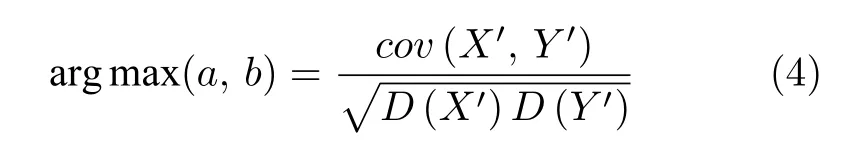
其中,a,b分别为X,Y的投影矩阵,X′=aTX,Y ′=aTY,cov为协方差,cov(X′,Y ′)协方差和方差的计算式为

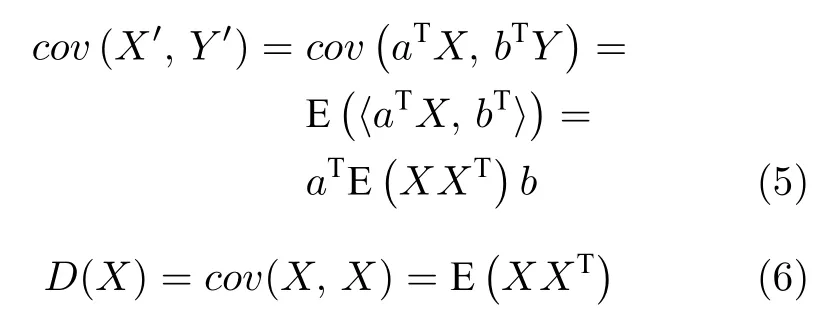
CCA的优化目标计算式为

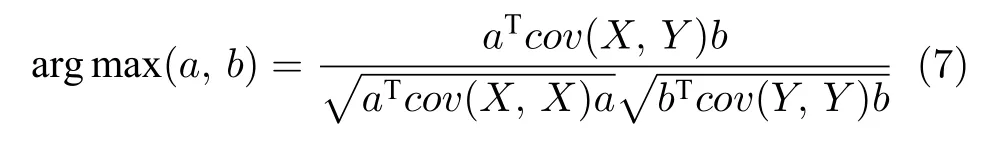
以CCA 为基础的子空间学习将大规模的数据样本进行优化,但它的计算复杂度很高,无法消除阶级间的相关性并无法限制类内的相关性.

2 深度时空图

针对DMM 时序信息的缺失的问题,本文提出一种深度图序列表示算法DSTM.DSTM 反映的是人体3D 时空行为在空间直角坐标轴上的分布随着时间变化的情况,人体所在空间直角坐标系三个轴分别为宽度轴(w)代表宽度方向、高度轴(h)代表高度方向、深度轴(d)代表深度方向,图1 为DSTM的流程图.

如图1 所示,首先将深度帧投影在三个笛卡尔正交面上,获得主视图、侧视图和俯视图三个2 维投影图,表示为mapv,v∈{f,s,t}.然后根据每个2 维投影图得到两个轴的行为分布情况.任选两个2 维投影图即可得到宽度轴、高度轴、深度轴的行为分布情况.

图1 DSTM 流程图Fig.1 DSTM flowchart

对a轴上的投影列表为

其中,a∈{w,h,d},W,H分别表示2 维投影图的宽度和高度.suma表示2 维投影图序列在a轴上投影列表.对2 维投影图序列在a轴上的投影列表进行二值化,即

其中,lista表示对2 维投影图序列在a轴上的投影列表进行二值化,a∈{w,h,d},ε表示二值化的阈值.假设有N帧投影,DSTM的计算式为

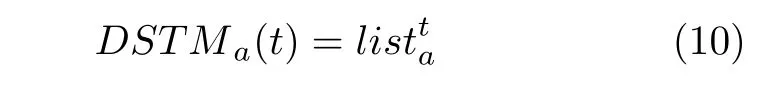
最后对DSTM进行感兴趣区域(Region of interest,ROI)处理,根据感兴趣区域的主旨,对图片进行裁剪、大小归一化处理.

3 多聚点子空间学习

子空间学习存在着计算复杂度高,无法消除阶级间相关性的缺陷,本文提出了多聚点子空间学习的方法,在约束平衡模态间样本关系的同时,通过构建同类别各样本的多个投影聚点,疏远不同类别样本的类间距离,降低了投影目标区域维度.多聚点子空间学习算法的思想可表示为

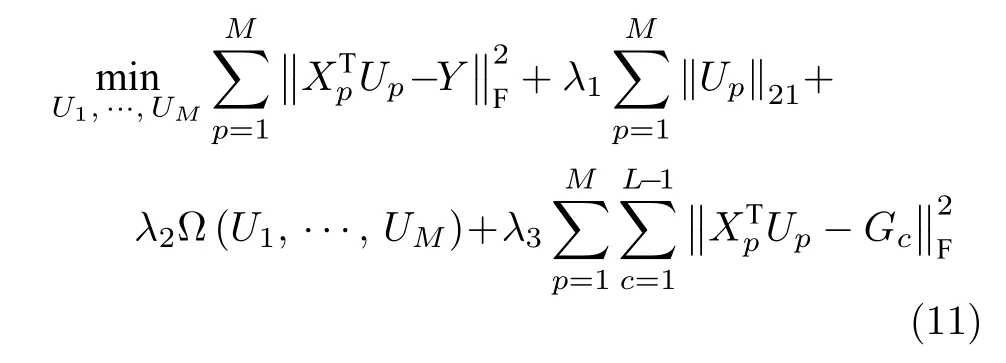
其中,Xp表示未经投影各模态样本,即原空间样本;Up,p=1,···,M表示各模态样本的投影矩阵;表示经投影后各模态样本,即子空间样本;L表示类别总数;Y为子空间内目标投影矩阵,由各类别样本目标投影聚点yi组成;Gc为多个各模态同一类别样本新建目标投影点矩阵;λ1,λ2,λ3为各项超参.

3.1 聚点与子空间学习

本文将传统子空间学习称为单聚点子空间学习.多聚点子空间学习与单聚点子空间学习的主要区别是聚点个数的不同,具体定义如下:

1)单聚点子空间学习.通过学习每种模态数据的投影矩阵,将不同类别数据投影到公共子空间.投影矩阵的学习通常是最小化投影后样本与各类数据唯一主聚点的距离得到,计算式为

其中,Y为子空间内目标投影矩阵,由各类别样本目标投影聚点yi组成,可表示为Y=[y1,y2,···,yN]T,

图2 为单聚点子空间学习.通过最小化子空间样本与各类别投影聚点之间距离来减少样本的类内距离.

图2 单聚点子空间学习Fig.2 Subspace learning

2)多聚点子空间学习.多聚点子空间学习是对单聚点子空间学习的优化,都是通过学习每种模态数据的投影矩阵,将不同类别数据投影到公共子空间.不同的是,投影矩阵的学习由同时最小化投影后样本与各类数据唯一主聚点以及与多个副聚点的总距离得到,计算式为

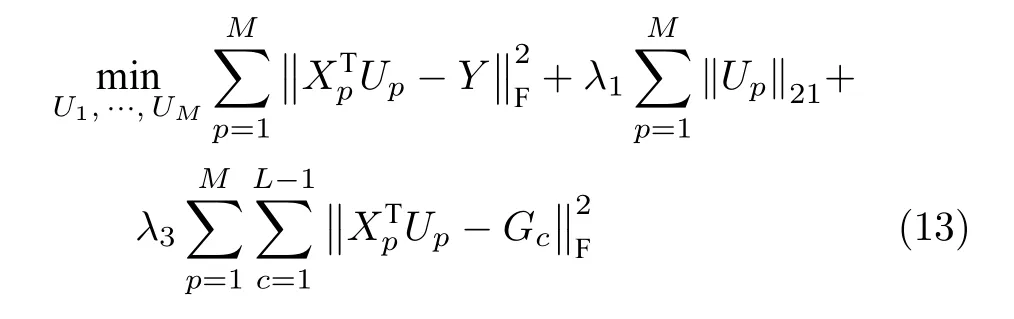
其中,Gc为各类别样本的第c个副投影聚点集合矩阵.副投影聚点为其他类别投影聚点关于当前类别目标投影聚点的对称聚点.Gc的构建算法步骤如下.

算法 1.Gc的构建算法

图3 为多聚点子空间学习.通过为各类别样本构建多个投影聚点并使用模态内、模态间数据相似度关系,使得子空间样本向多个投影目标点附近的超平面聚拢,有效增大了子空间样本之间的距离,降低了投影目标区域的维度,使投影目标区域从n维的超球体变为n-1 维的超平面,同类别的子空间样本更为紧凑,从而有效地提高了算法的特征优化效果.因此结合使用数据模态内、模态间相似度关系的多聚点子空间学习可表示为

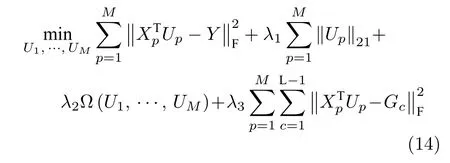
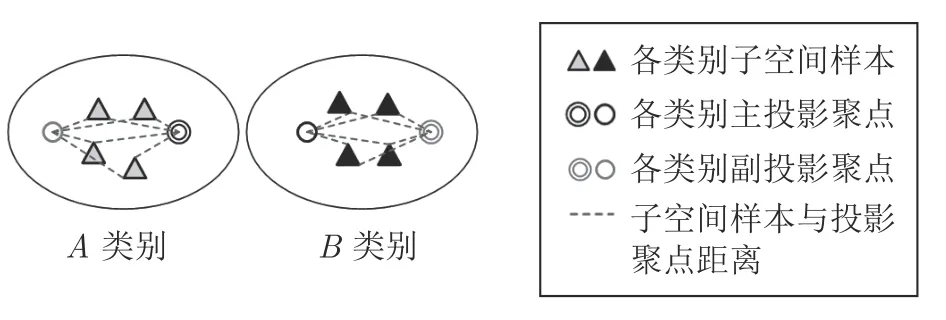
图3 多聚点子空间学习Fig.3 Multi-center subspace learning

3.2 超参计算

本文以式(14)第1 项为基准确定式中各项超参,设定子空间样本与目标投影聚点之间约束程度等同于同类别子空间样本之间约束程度.第1 项中子空间样本与目标投影点之间约束共有F1个,F1计算式为

其中,M为模态数,N为样本数.

式(14)第3 项中子空间样本之间约束共有F2个,其中同一模态子空间样本相似度的约束共有Fa个,不同模态同一类别的子空间样本之间的相似度的约束共有Fb个,F2,Fa,Fb计算式为

式(14)第4 项中子空间样本与目标投影聚点之间约束共有F3个,F3计算式为

在子空间样本与目标投影聚点之间约束程度等同于同类别子空间样本之间约束.根据F1,F2,F3比例关系,可以确定式(14)的第3 项和第4 项超参的计算式为

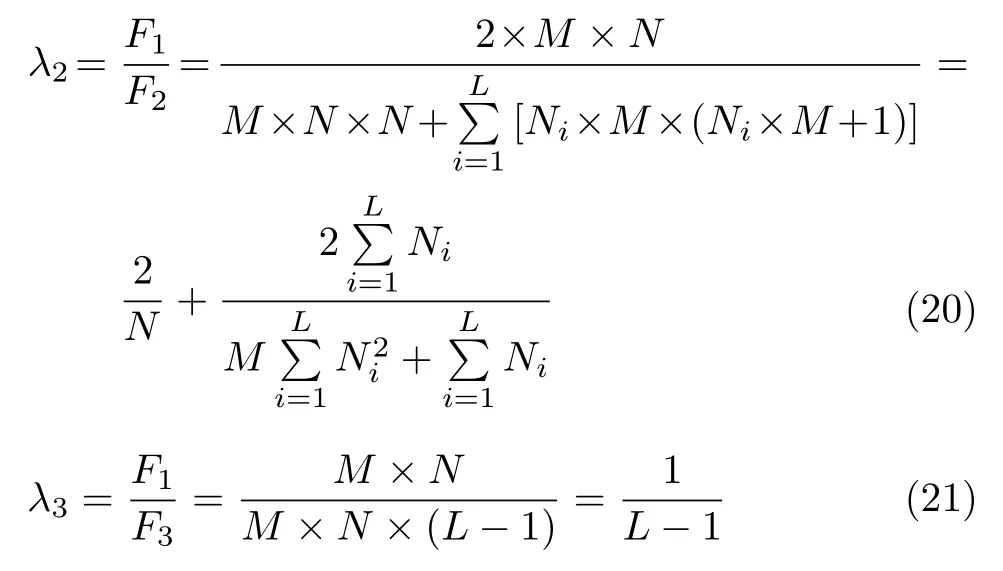
最后本文通过实验,以最终识别率为依据,确定λ1.

3.3 公式优化与投影矩阵求取

对于式(16)中的几项可进行优化,式(16)中的第2 项是对各模态的数据样本投影矩阵的约束项,防止算法过拟合.第2 项中含有l2,1范数,它是非平滑且不能得到的一个闭式解[28].对于投影矩阵,其l2,1范数定义为

式(14)中第3 项是不同模态同一类别的子空间样本之间的约束.第3 项可以通过如下方式进行推导

本节通过下述算法步骤求解线性系统问题来计算式(26)的最优解.

算法 2.计算子空间学习的最优解

通过算法2 进行求解,先计算出拉普拉斯矩阵,然后求解出并代入式(27)进行重复求解,直至收敛.

4 实验结果与分析

4.1 数据库

文献[30]对数据集进行了详细的研究，本文采用的是由Kinect 摄像头采集的MSR-Action3D[31]数据库和UTD-MHAD[32]数据库.

MSR-Action3D (MSR)数据库由10 个人20个动作重复 2～3 次,共计557 个深度图序列,涉及人的全身动作.详情如表1 所示.

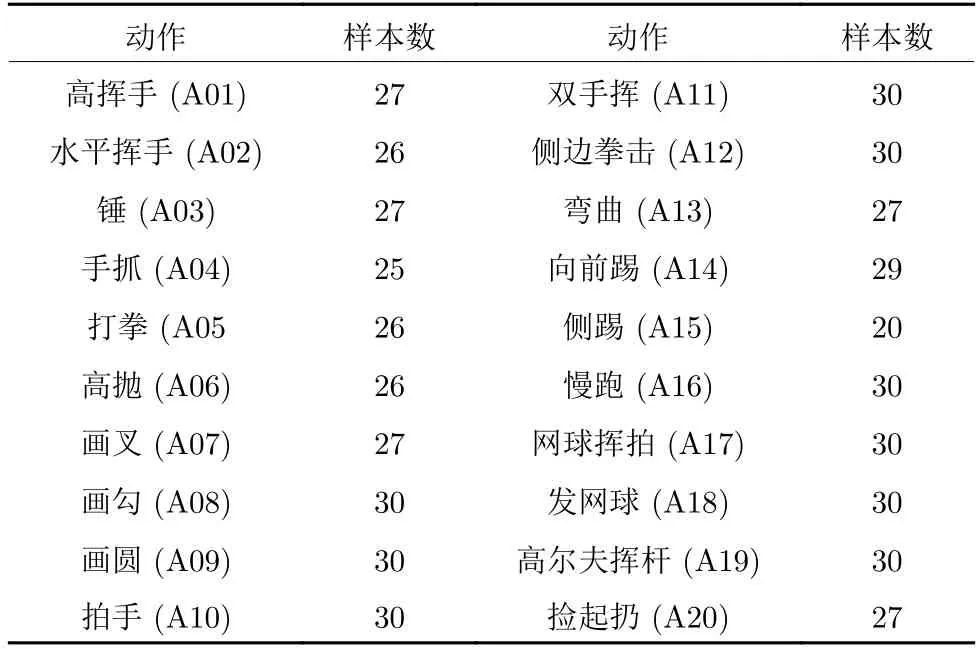
表1 MSR 数据库中的人体行为Table 1 Human actions in MSR

UTD-MHAD (UTD)数据库由8 个人(4男4 女)27 个动作重复4 次,共计861 个深度图序列.详情如表2 所示.

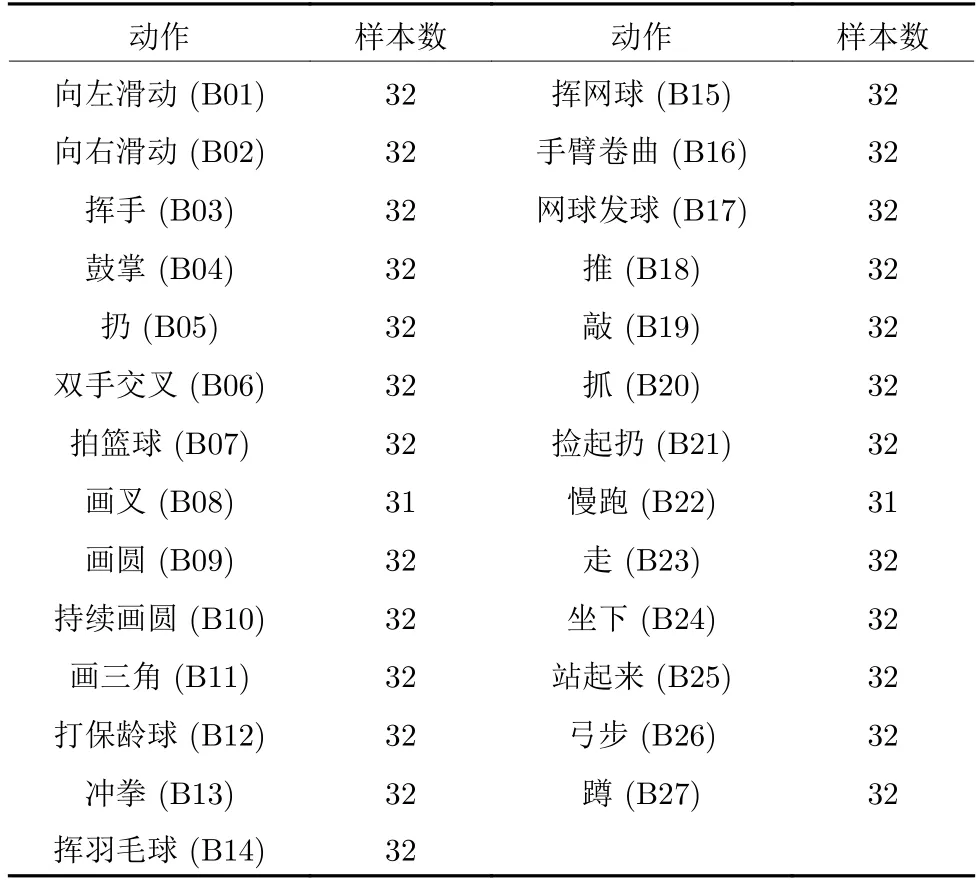
表2 UTD 数据库中的人体行为Table 2 Human actions in UTD

为了验证时序信息在人体行为中的重要性,本文将与原深度图序列顺序相反的行为称为反序行为.本文中的反序行为是通过将正序行为的深度图序列进行反序排列操作得到新数据库D1,D2,其中D1 为MSR 数据库及MSR 反序数据库,D2 为UTD 数据库及UTD 反序数据库.D1 正反高抛动作如图4 所示.

图4 正反高抛动作Fig.4 Positive and negative high throwing action

4.2 实验设置

本文采用10×10 像素的图像单元分割图像,每2×2 个图像单元构成一个图像块,以10 像素为步长滑动图像块来提取图像的方向梯度直方图(Histogram of oriented gradient,HOG)[26]特征.采用采样半径为2,采样点数为8的参数设置来提取图像局部二值模式 (Local binary patterns,LBP)[33]特征.尺寸归一化后DMMf大小为320×240,DMMs大小为500×240,DMMt大小为320×500,所以DMM-HOG的特征数量为120 924.DMMLBP的特征数量为276 800.同样尺寸归一化后DSTMw大小为320×60,DSTMh大小为240×60,DSTMd大小为500×60,所以DMM-HOG的特征数量为18 540.DMM-LBP的特征数量为63 600.

实验中分为两个设置.设置1 在MSR 数据库上将20 个行为分为3 组(AS1、AS2、AS3)[33],行为分布情况如表1,其中AS1 和AS2 组内相似度较高,AS3 组内相似度较低.如表3 所示.

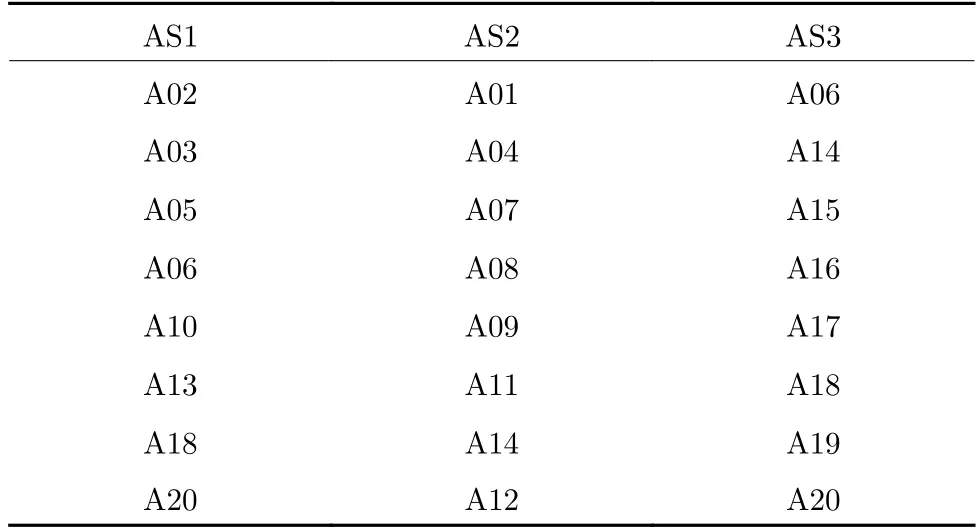
表3 MSR-Action3D 数据分组Table 3 MSR-Action3D data grouping

设置2 在MSR 数据库和UTD 数据库上选取全部的动作.

在设置1 和设置2 中可采用4 种测试方法.测试1:1/3 作为训练数据,2/3 作为测试数据;测试2[12]:1/2 作为训练数据,1/2 作为测试数据;测试3:2/3 作为训练数据,1/3 作为测试数据;测试4:采用5 折交叉验证

4.3 参数设置

在本文提出的人体识别的模型中,首先要确定参数λ1,λ2,λ3的值.在进行子空间学习的时候,参数对于结果有着巨大的影响,需要优先估计最优的参数.通过选择不同的参数,并以识别率作为评判标准.识别率=预测正确测试样本数/总测试样本数.通过采用设置1 测试1的方法和HOG 特征进行实验.根据式(20)和式(21)分别可以得到λ2=1/13 847,λ3=1/19.根据图5 可知,当λ1=20时,本文算法具有较高的人体识别性能.

图5 参数选择Fig.5 The parameter of selection

4.4 实验结果分析

4.4.1 分类器选择

对同一种特征图而言,采用不同的分类器识别效果会有较大的差异.为了选择对特征图识别效果较好的分类器,本实验通过比较DSTM 在不同的分类器的识别效果,最终以识别率作为标准,采用设置1 测试3的方法,如图6 所示.

从图6 中可以发现HOG 特征采用了不同的分类器,得到的识别率差异较大,不同特征图采用同一分类器,与同一特征图采用不同分类器,支持向量机(Support vector machine,SVM)的识别效果较好,下面实验均采用SVM 作为分类器.

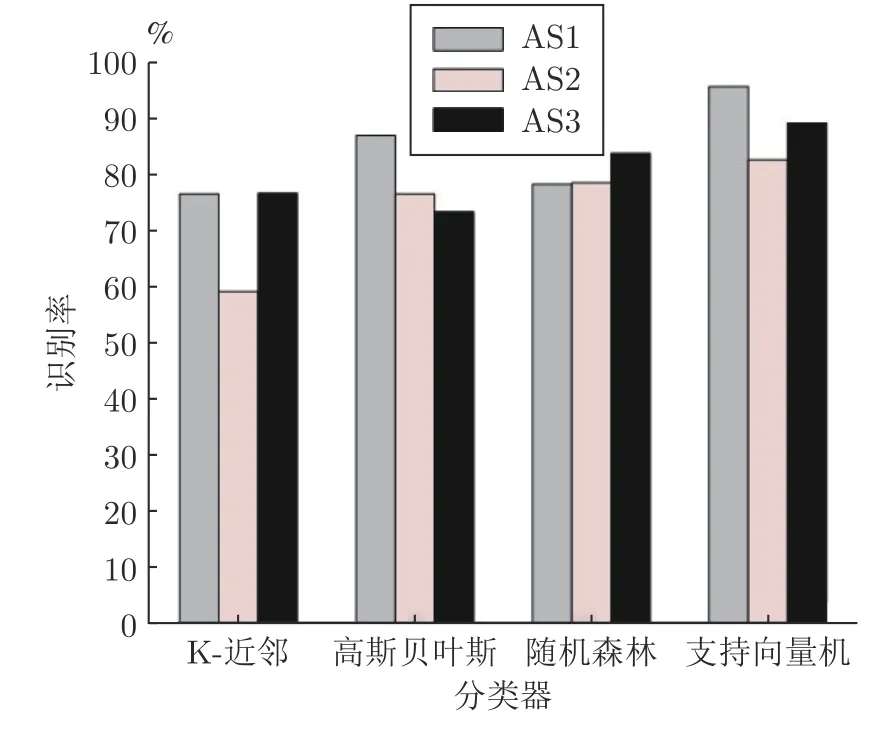
图6 DSTM 在不同分类器识别效果Fig.6 DSTM recognition of different classifiers

4.4.2 特征选择

为了筛出空间信息和时序信息的特征图,采用设置1,在MSR 数据库上使用测试1、测试2、测试4的方法进行实验,并且对3 组实验结果设置了平均值;采用设置2,在UTD 数据库上使用测试1、测试2、测试3的方法进行实验.通过个体识别率和平均识别率来筛出空间信息和时序信息的特征图.

表4 和表5 使用HOG 和LBP 两个特征图序列.由表4 中的单个识别率或平均识别率以及表5中所有动作的识别率可以得出结论:在同一特征图中,HOG 特征较LBP 特征有着更高的识别率.LBP 特征反映的是像素周围区域的纹理信息;HOG 特征能捕获轮廓、弱化光照,对于深度图有着更佳的表现,有着更好的识别效果.就本文实验而言.HOG特征更适合于本实验.

在表4 和表5 中选择同为HOG 特征的特征图,从表中的识别率可以得出,DMM 和DSTM 与MEI 和MHI 相比有更高的识别率.主要原因是MEI 将深度帧二值化后进行叠加,掩盖了时序图中每张图的轮廓信息,丢失了时序图自身的深度信息,但反映出一定的轮廓信息,保留了一定的空间信息;MHI 虽然通过图像的亮度衰减,增加了一部分时序信息,但由于人为干预图像的亮度,导致了图像自身的深度信息的丢失.

表4 MSR 数据库上不同特征的识别率(%)Table 4 Different of feature action recognition on MSR (%)

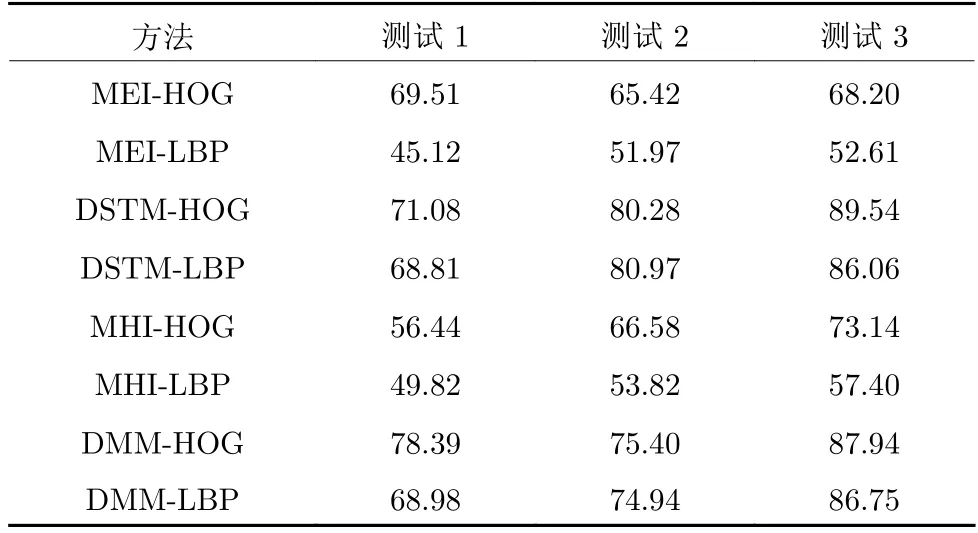
表5 UTD 数据库上不同特征的识别率(%)Table 5 Different of feature action recognition on UTD (%)

使用DSTM 和DMM的优势主要有以下几点:1)DMM 是将深度帧投影到笛卡尔直角坐标平面上,生成主视图、俯视图、侧视图三个2 维地图,在此基础上差分堆叠整个深度序列动作能量图.相较于MEI,DMM 充分地使用了时序图的深度信息,丰富了特征中的空间信息,很大程度上保留了轮廓信息,并且从三个方向上可以很明显地看出行为动作,充分展现了空间信息.2)DSTM 是将深度帧投影到笛卡尔直角坐标平面上,生成主视图、俯视图、侧视图三个2 维地图,提取任意两个2 维地图投影到3 个正交轴上获取三轴坐标投影,将获得的坐标投影二值化后按时间顺序进行拼接.DSTM 将深度帧的时序信息很好地保留了下来,相较于MHI 有了很大程度上的改善.DSTM 较好地保存了时序信息.

时序信息在行为识别中有着重要的作用.对比DMM,DSTM 蕴含着重要的时序信息.本文在D1和D2 数据库上采用设置2,使用测试1的方法

通过对比表6的识别率和表7的时间复杂度,在D1 与D2 数据库的实验证明,DMM 由于未含有时序信息，与DSTM 识别率差异较大.另外DMM相较于DSTM 时间复杂度较高,DSTM的时序信息在行为识别中起着重要的作用.

表6 DMM 和DSTM 对比实验结果(%)Table 6 Experimental results of DMM and DSTM (%)

表7 DMM 和DSTM 平均处理时间(s)Table 7 Average processing time of DMM and DSTM (s)

4.4.3 特征选择实验结果

本文选取的深度运动图代表的空间信息与深度时空图代表的特征图使用多聚点子空间学习的算法(简称本文方法).为了表征本文方法对于单一特征有着更高的识别率以及本文方法对于融合方法同样有着更高的识别率,将本文方法与当前主流单一算法和融合算法进行比较.在MSD-Action3D 上采用设置2 测试2、设置2 测试4的方法;在UTD-MHAD上采用设置2 测试4的方法.

表8 均采用文献[12]方法中的实验设置，其中文献[34-40]方法使用了深度学习的模型框架.识别率最高为91.45.本文的识别率达到了90.32%，接近文献[34]中的最优结果,主要原因是:本文提出的DSTM 算法可以将深度帧的时序信息很好地保留下来，获得的特征信息更加丰富和完善.多聚点子空间的方法构建了多个投影聚点并使用了模态内、模态间数据相似度关系,使得子空间样本向多个投影目标点附近的超平面聚拢,有效增大了子空间样本之间的距离,所以在行为识别中表现出了较为优越的性能.表9 和表10 在多聚点子空间学习加单个特征图的识别率有一定的提升，但相较于融合DSTM 特征和DMM 特征图略有不足.本文在采用不同的融合方法时,识别率也有一定提升.本文方法的识别率在MSR 数据库达到98.21%和UTD数据库达到98.84%.为了更深层次的了解本文方法的识别效果,本文给出了本文方法的每个动作识别效果的混淆矩阵.

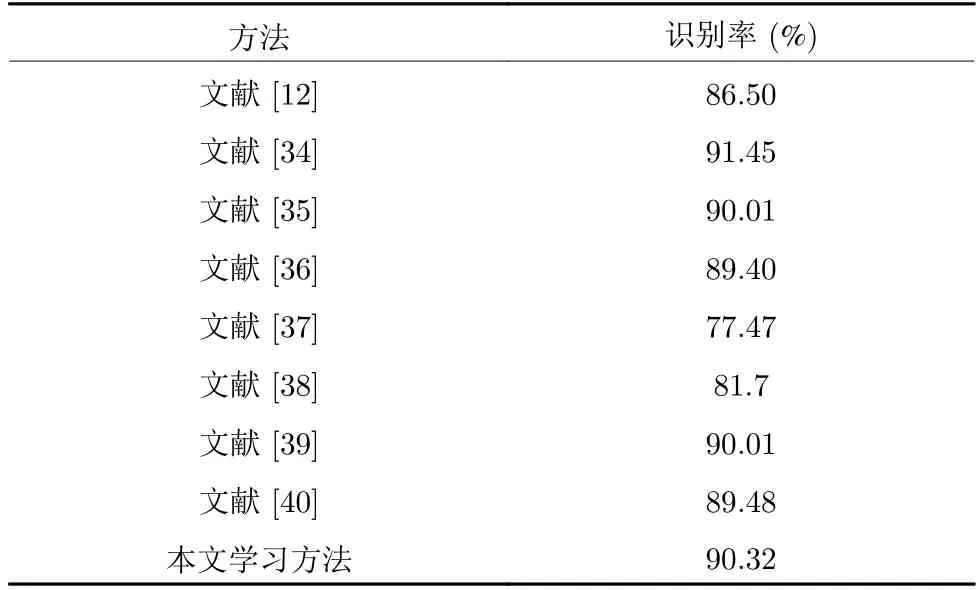
表8 M SR-Action3D1 上的实验结果Table 8 Experimental results onMSR-Action3D1

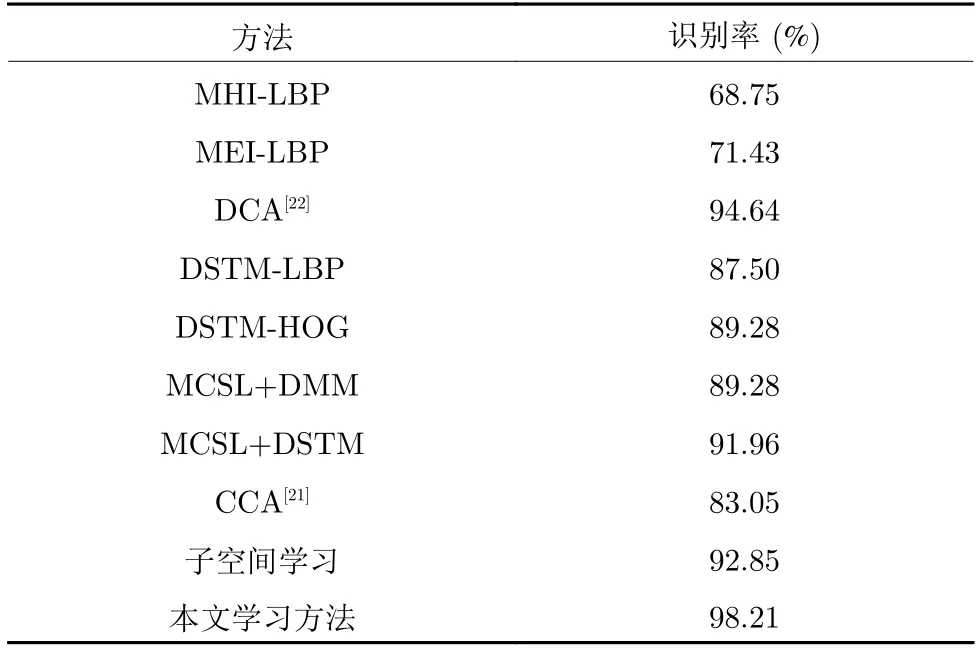
表9 M SR-Action3D2 上的实验结果Table 9 Experimental results onMSR-Action3D2

表10 UTD-MHAD 在设置2 测试4 上的实验结果Table 10 Experimental results on UTD-MHAD

本文通过融合DMM的空间信息和DSTM的时序信息的两种特征图后,得到空间时序特征.多聚点子空间学习是通过为各类别样本构建了多个投影聚点.图7(a)和图7(b)为MSR的混淆矩阵.其中,MSR-Action3D1采用设置2 测试2;MSR-Action3D2采用设置2 测试4.从中可以看出整体识别率,图中显示本文方法将画叉识别成画圈,将发网球识别成了画勾.两类动作差异性小,因此较容易出错.图7 (c)为UTD的混淆矩阵,图中显示本文方法将慢跑变成走路.出现错误原因是动作行为轨迹相似性较大.

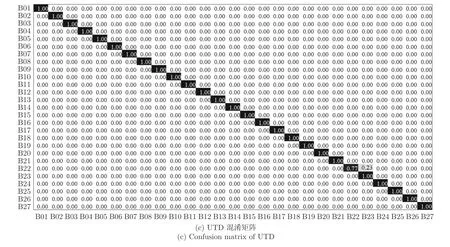
图7 混淆矩阵Fig.7 Confusion matrix

5 结束语

针对现有的深度图序列特征图冗余过多、时序和空间信息缺失等问题,本文提出一种新的深度序列表示方式DSTM 和多聚点子空间学习,并在此基础上进行了人体行为识别研究.深度帧投影二值化后按时间顺序进行拼接生成DSTM,对每张DSTM 提取HOG 特征以获得时序信息.对DMM提取HOG 特征以获得空间信息.多聚点子空间学习,在约束平衡模态间样本关系的同时,构建同类别各样本的多个副投影聚点,疏远不同类别样本的类间距离,降低了投影目标区域维度,最后送入分类器进行人体行为识别.本实验表明本文提出的DSTM 和多聚点子空间学习的方法能够减少深度序列的冗余,保留丰富的空间信息和良好的时序信息,有效地提高行为识别的准确性.