分布式水土流失型面源污染模型初探
朱凯航,陈磊*,王怡雯,刘国王辰,颜小曼,郭晨茜,张亮,沈珍瑶
(1.北京师范大学环境学院,北京 100875;2.中国科学院精密测量科学与技术创新研究院,武汉 430077)
水土流失和面源污染是两个密切相关的全球环境问题[1-2]。在我国,人为扰动和不当的土地利用方式加速了水土流失过程,2021 年全国水土流失面积为267.42 万km2,占国土面积的27.96%。水土流失过程中不仅土壤颗粒被冲刷进入河道,引起泥沙淤积,而且其伴生的面源污染还会引起水质恶化,导致湖泊富营养化等环境问题[3-4]。水土流失、面源污染二者互相影响、互相制约,共同导致了水土流失型面源污染。
水土流失型面源污染涉及水、土、污染物等多介质耦合作用,主要包含降雨径流、土壤侵蚀和泥沙/污染物运输3 个过程[5],涉及农田、沟渠、水塘、湿地、河滨等多个环节和田块、灌排单元、集水区、流域等多个尺度[6]。水土流失型面源污染的产生和传输具有不确定性和复杂性,对其关键过程的正确模拟与评估对污染入水体量有重要影响[7]。目前多采用面源污染模型对水土流失和面源污染进行模拟,如SWAT(Soil and Water Assessment Tool)、HSPF(Hydrological Simu⁃lation Program:Fortran)、AGNPS(Agricultural Nonpoint Pollution Source Model)等[8-9]。但是此类模型集总式或半分布式的建模思路忽略了集水区内部地形特征、径流路径、景观格局等因素的差异对水土流失和污染物传输造成的影响,并且无法考虑水土流失和污染物在传输中的损失[7],不适用于我国中西部景观破碎度较高、空间异质性强的丘陵地区。因此,充分考虑水土流失型面源污染的微观机理,精准模拟水土流失型面源污染的陆面传输过程,识别水土流失型面源污染优先控制区,是准确评估水土流失型面源污染风险和形成防控技术的基础[10-11]。
本文针对现有半分布式模型的局限性,构建了耦合田块尺度富集/流失、流域尺度传输及河道迁移过程的分布式水土流失型面源污染模型,开发出高效栅格汇流算法,破解了对丘陵山区水土流失型面源污染精准评估和防控的技术瓶颈问题。进而本研究以三峡库区菁林溪流域为案例区,对新模型进行验证,基于新模型识别了三峡库区典型流域的水土流失型面源污染时空分布规律,评价了典型措施的防控效果,以期为水土流失型面源污染防控提供机理和技术支持。
1 材料与方法
1.1 研究区概况
菁林溪流域位于三峡库区澎溪河上游(31.19°~31.27°N,108.34°~108.38°E,图1),流域面积9.51 km2,高程位于665~1 117 m之间,流域上游高程差较大,中下游相对平坦,农业种植较发达[12]。该地多年平均气温22.1 ℃,平均降水1 293 mm,5—9 月的降水量占全年的66%以上。本研究日气象数据来源于重庆市统计年鉴。DEM 数据来源于中国科学院资源环境科学与数据中心(http://www.resdc.cn/)。土壤类型数据参考吕明权[13]对研究区土壤样品进行实测得到的数据,主要有三类土壤:粗骨土、水稻土和紫色土。土地利用类型来源于对高精度遥感影像的人工划分,主要由林地、水田、坡耕地、建设用地、河道及池塘等水体组成。作物管理数据(作物种类、种植时间、化肥施用情况)通过实地调研获取。本研究开展了多年的流域水量水质观测,使用自动水位检测仪HOBO UL20获取每日的流量数据,通过人工采集后在实验室测定获取水质数据,采样点位于流域主干道,于每月初、月中以及降雨日进行采样,使用0.45µm滤膜过滤水样,以钼酸铵分光光度法测定水样中的总磷与溶解态磷浓度,吸附态磷浓度为二者之差,相关数据用于后续模型构建与验证。

图1 菁林溪流域地理位置与土地利用状况Figure 1 Location and land use of Jinglinxi watershed
1.2 模型构建
面源污染物在降雨、地形等因素驱动下离开产污单元,并伴随泥沙和径流进入河道。本研究的栅格模型考虑了土壤原位剥离、溶解态和吸附态面源污染物流失及其微观传输规律,重点包括田块富集/流失模块、流域汇流/拦截模块、河道传输模块。
1.2.1 田块富集/流失模块
(1)降雨产流模拟
由于大部分流域都没有降雨-径流的历史数据,因此选取SCS-CN 法,该方法因对数据要求较低、对径流模拟效果较好而得到广泛应用[14]。在SCS-CN方法中,首先对研究区的降雨量数据进行空间插值,计算月降雨的空间分布情况,再结合相关研究,对研究区曲线数(CN)和初损量进行修正,计算地表径流,计算公式为:

式中:Qsurf为地表径流,mm;Rday为降雨量,mm;Ia为初损量,包括产流前的地面填洼量、植物截留量和下渗量,mm;S为最大蓄水量,mm。

式中:CN表示某天的曲线数。Ia通常近似为0.2S,因此公式(1)变为:

(2)土壤侵蚀模拟
模型采用RUSLE 方程对泥沙的原位负荷量进行模拟[15]:

式中:sed为某栅格的泥沙日负荷量,t·d-1;R为降雨侵蚀力因子,MJ·mm·hm-2·h-1·d-1;K为土壤可蚀性因子,t·hm2·h·MJ-1·mm-1·hm-2;L为坡长因子,无量纲;S为坡度因子,无量纲;C为植被覆盖与管理因子,无量纲;P为水土保持措施因子,无量纲;cellsize为栅格的面积,30 m×30 m的栅格面积为0.09 hm2。
降雨侵蚀力因子(R)为降雨作用对土壤剥蚀的能量因子,本研究选择基于逐日降水数据的R因子计算方式,计算公式为:

式中:Pi为当日降水量,降雨量不足12 mm 时取0;Pd12和Py12分别为降水量大于12 mm的日平均降水量和年平均降水量,mm;α和β为计算参数,与降雨强度和降雨频率相关。
土壤可蚀性因子(K)定量描述了土壤对降雨侵蚀的抵抗能力,其主要受土壤质地、土壤颗粒组成和土壤结构等物理因素的影响。由于研究区位于三峡库区,本研究采用吴昌广等[16]基于重庆市和湖北省各土种的理化性质数据库提出的三峡库区土壤可蚀性。
土壤侵蚀量随着坡长和坡度的增加而增加,坡长因子(L)和坡度因子(S)全面反映了地形对土壤侵蚀造成的影响,计算公式为:

式中:λ为坡长的水平投影,m;m为坡长指数,无量纲;θ为坡度,(°)。
植被覆盖与管理因子(C)反映了植被对降雨径流和水土流失的拦截作用。本研究基于归一化植被指数推算C因子值,遥感数据来自美国国家航空航天局(NASA)的 EOS/MODIS 数据产品(https://ladsweb.modaps.eosdis.nasa.gov),计算公式为:

式中:NDVI为归一化植被指数;NDVImin和NDVImax为一定置信区间内的NDVI最小值和最大值(3%~97%)。
水土保持措施因子(P)为采取特定水土保持措施下的水土流失量与未采取任何保持措施情况下的水土流失量之比,林地、旱地、水田、水域和建设用地的P因子分别为0.90、0.35、0.25、0和1.0[17]。
(3)土壤磷富集、流失模拟
模型的磷循环模块借鉴SWAT 模型磷库的思路[18],将土壤中的无机磷划分为溶解态无机磷库、活性态无机磷库和稳定态无机磷库,将有机磷划分为活性态有机磷库、稳定态有机磷库和新生有机磷库,磷循环模块在栅格的尺度上进行,磷循环过程如图2所示。
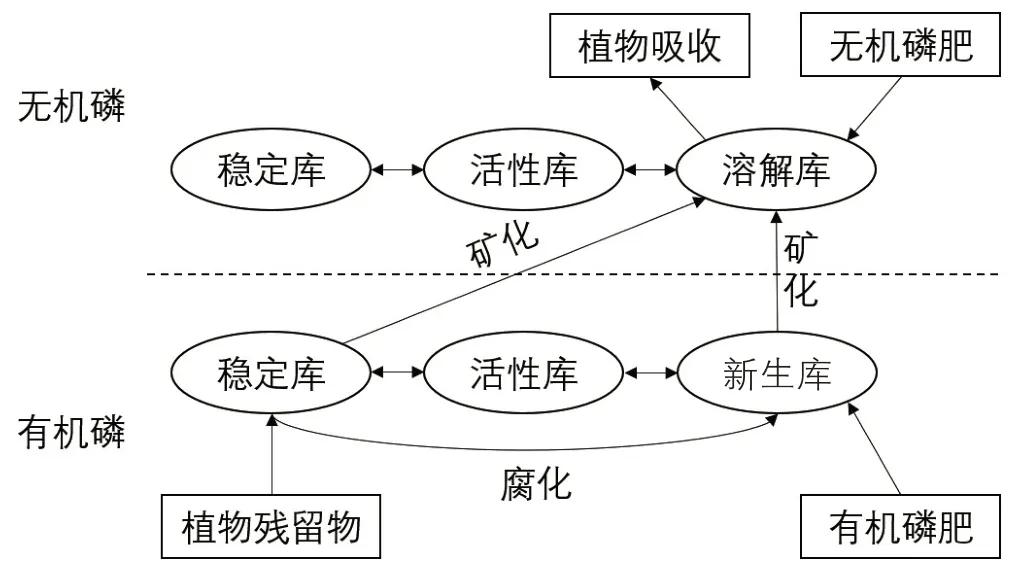
图2 土壤磷循环流程Figure 2 Circulation of soil phosphorus
土壤中的可溶性磷主要通过扩散作用迁移,由于地表径流仅与表层10 mm 土层中的部分可溶性磷相互作用,因此某栅格某月的溶解态磷负荷量计算公式为:

式中:Psol为某栅格的溶解态磷月负荷量,kg;Psol,surf,i为某月第i天表层10 mm 土层中的可溶性磷量,kg·hm-2;Qsurf,i为某月第i天的地表径流量,mm;ρb为表层10 mm 土层的容重,Mg·m-3;depthsurf为土壤表层的深度,10 mm;kd,surf为磷的土壤分配系数,是表层 10 mm土层中的可溶性磷浓度与地表径流中的可溶性磷浓度的比值,m3·Mg-1;cellsize为栅格的面积,0.09 hm2;m为某月的天数,d。
吸附态磷以泥沙的形式进入河道,某栅格某月的吸附态磷负荷量为:

式中:Psed为某栅格的吸附态磷月负荷量,kg;concsedP,i为某月第i天表层10 mm 土层中吸附在泥沙上的磷量,g·t-1;sedi为某月第i天的泥沙月负荷量,t;εP:sed为磷的富集比。
表层10 mm 土层中吸附在泥沙上的磷量(conc⁃sedP)计算公式为:

式中:minPact,surf为表土层中活性态无机磷库中的磷含量,kg·hm-2;minPsta,surf为表土层中稳定态无机磷库中的磷含量,kg·hm-2;orgPhum,surf为表土层中腐殖质有机磷库中的磷含量,kg·hm-2;orgPfrsh,surf为表土层中新生有机磷库中的磷含量,kg·hm-2;ρb为表层 10 mm 土层的容重,Mg·m-3;depthsurf为土壤表层的深度,10 mm。
富集比(εP:sed)定义为随泥沙迁移的磷含量与土壤表层中磷含量的比值,计算公式为:
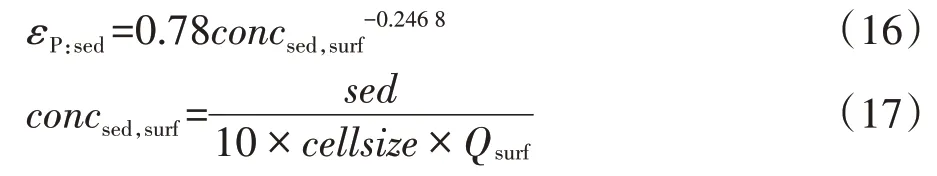
式中:concsed,surf为地表径流中的含沙量,Mg·m-3;sed为某日的产沙量,t;cellsize为栅格的面积,0.09 hm2;Qsurf为某日的地表径流量,mm。
1.2.2 流域汇流/拦截模块
传统的栅格汇流算法是基于源头到出口的正向思路实现的[19],但是正向计算的思路存在计算效率低的问题,因此本研究提出了结合反向递归及哈希表的优化算法。具体步骤如下:
(1)基于D8算法获得栅格之间的上下游关系,构建一个字典保存栅格之间的上下游关系,字典的值保存了某一栅格所有上游栅格的集合,键则为下游栅格(图3b)。字典基于哈希算法实现,键名是唯一、不能重复的,因此只需要以接近常量的时间便可以查询某一栅格的所有上游栅格,无需遍历字典中的所有元素。在查询某一栅格的上游栅格时,查询时间并不会随着流域面积(字典长度)的增大而增大。
(2)基于递归算法,从流域出口反向索引栅格之间的上下游关系,对全流域栅格进行汇流计算。递归算法是在函数中直接或调用自身的算法。在汇流计算时,对流域出口栅格进行反向递归索引:首先在字典中查询该栅格,如果不存在则表明该栅格不存在上游栅格,因此可直接基于该栅格的源图层进行计算;如果该栅格存在于字典中,说明该栅格存在上游栅格,则需对其所有上游栅格再次进行反向递归索引,重复以上判断,待所有上游节点完成模拟并返回结果时,再基于上游栅格的模拟结果及该栅格的源图层进行模拟。以图3a 所示的传输路径为例,其模拟步骤如下:

图3 模型构建流程图Figure 3 Flow chart of model construction
①从出口栅格4 号栅格开始索引,在传输字典中索引到了它的上游栅格2 号栅格,于是对2 号栅格进行索引,待2号栅格的模拟结果返回后,再对4号栅格进行模拟。
②对2 号栅格进行索引,在传输字典中索引到了它的上游栅格1 号栅格和3 号栅格,于是先对1 号栅格和3 号栅格进行模拟,待1 号栅格和3 号栅格的模拟结果返回后,再对2号栅格进行模拟。
③对1 号栅格进行索引,发现1 号栅格无上游栅格,则直接进行该栅格的模拟,并将模拟结果返回给2号栅格;对3号栅格进行索引,索引到了它的上游栅格5号栅格和6号栅格,于是先对5号栅格和6号栅格进行模拟,基于5 号栅格和6 号栅格的入流情况对3号栅格进行模拟。
④对5 号栅格和6 号栅格进行索引,发现二者无上游栅格,则直接进行模拟,并将模拟结果返回给3号栅格。
假设某流域一共有n个栅格,从流域出口反向递归索引保证一次模拟只需要进行n次计算,而正向计算需要不断地判断上下游关系,计算次数可能会达到n2次甚至n3次。经过递归算法和哈希表的优化,所构建分布式模型的运行时间只会随流域面积的增大及内部方程的增多线性增长而不是指数增长,这为后续的高效计算和率定奠定了基础。
在传输过程中,主要考虑水塘与植被过滤带对水、沙、污染物的拦截作用。
(1)水塘拦截
水塘的拦沙效率计算公式为:

式中:trap为拦沙效率,%;Vset为泥沙沉降速率,m·d-1;Vovfl为出流速率,m·d-1;Q0表示水塘的出流量,m3·s-1;SAres表示水塘的水面面积,hm2。
(2)植被过滤带
本模型基于邓娜等[20]提出的植被过滤带净化效果多元非线性回归方程,模拟传输路径上植被对泥沙、径流和吸附态磷的拦截效果,计算公式为:
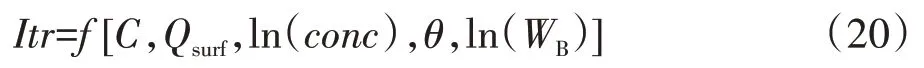
式中:Itr为植被过滤带对泥沙、径流和吸附态磷的拦截比例,%;C为植被覆盖与管理因子,无量纲;Qsurf为地表径流,mm;conc为入流的泥沙、吸附态磷的浓度,mg·L-1;θ为坡度,(°);WB为植被过滤带宽度,m。
1.2.3 河道传输模块
(1)泥沙沉降/再悬浮模拟
本模型采用MOLINAS 等[21]提出的基于通用河流功率的泥沙搬运方程计算河道搬运的最大含沙量:

式中:concsed,ch,mx为河道能搬运的最大含沙量,t·m-3;Sg为河道中固体的相对密度,2.65;Cw为河道含沙量,kg·m-3;ψ为通用河道功率;depth表示河道深度,m;D50表示泥沙的中值粒径,mm。
大于河道最大含沙量部分的泥沙储存在当前的河道栅格中,直到下次河道含沙量小于最大含沙量时,发生再悬浮。
(2)河道磷循环模拟
在水体中,藻类死亡后藻体磷转化为有机磷,有机磷可通过矿化作用转化为能被藻类吸收的可溶性磷,也可通过沉降作用从水流中去除。本模型借鉴SWAT 模型中河道磷循环过程的相关方程,某日有机磷浓度的变化量为:
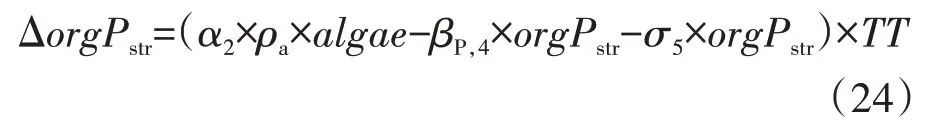
式中:α2为藻体磷占藻类生物质的比例,无量纲;ρa为当地藻类的呼吸强度或死亡率,d-1;algea为某日初始时刻藻类的生物质浓度,mg·L-1;βP,4为有机磷的成矿速率常数,d-1;orgPstr为某日初始时刻有机磷的浓度,mg·L-1;σ5为有机磷的沉降速率系数,d-1;TT为河段的水流运动时间,d。
某日可溶性磷的浓度变化量为:
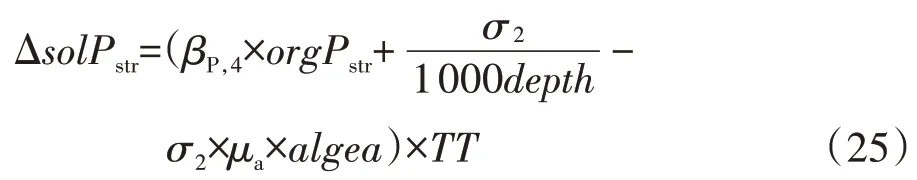
式中:σ2为沉积物提供可溶性磷的速率,mg·m-2·d-1;depth为河道水深,m;μa为当地藻类的生长率,d-1。与藻类相关的参数均为待率定参数。
1.3 模型应用
本模型代码实现主要基于Python 3.9 编程语言,使用pandas(csv 文件的读取与操作)和gdal(栅格文件与csv 文件的互相转换)等基础包实现计算。模拟时将土地利用、土壤类型、径流流向、坡度、降雨量、产流量、水土流失量等基础数据转换为csv文件,将单元格视作栅格,在Python 脚本中模拟计算水土流失、径流与污染物的源-流-汇过程,模型的运行步长为月。
本模型共涉及35 个参数,以纳什效率系数(NSE)、决定系数(R2)和百分比偏差(PBIAS)为优化目标进行模型参数率定。

式中:Oi为每月观测值;Pi为每月模拟值为每月观测值的平均值为每月模拟值的平均值。
由于涉及35 个待率定参数,以及3 个率定指标,因此模型率定属于典型NP-HARD 问题,在解决该问题的方法中以带有精英保留策略的NSGA-Ⅱ算法运用最为广泛[22]。但在实际应用中NSGA-Ⅱ算法的性能会随着优化目标的扩展和优化问题的复杂化而受到显著影响。因此本研究使用2014 年DEBK 提出的NSGA-Ⅲ算法对模型的参数进行率定。通过引入广泛分布参考点维持种群多样性并对拥挤排序进行改编,NSGA-Ⅲ算法具有良好的搜索高维空间中解的能力,在参数率定中得到了广泛的应用[23]。各参数设置如表1所示。

表1 NSGA-Ⅲ算法参数取值Table 1 Parameters of NSAG-Ⅲalgorithm
分布式模型提供的高精度的污染源空间分布为防控措施的模拟提供了基础。基于不同的栅格尺度源图层,如水土流失图层、土壤磷含量图层、土地利用图层等,本研究分别评估了退耕还林、化肥减量、坡改梯、滨岸缓冲带等措施对面源污染的削减效率,为水土流失型面源污染的防控提供依据,提出了5 种模拟情景。情景1:基准情景,不做任何的修改;情景2:基于流域多年水土流失情况,对水土流失强度前30%栅格上的坡耕地进行退耕还林;情景3:基于土壤磷含量图层,对土壤磷含量前30%的坡耕地/水田化肥减量50%;情景4:基于坡度图层,对坡度>10°的坡耕地实施坡改梯措施;情景5:基于河道图层与污染传输图层,识别在总磷入河量前30%的滨岸栅格,并设置30 m滨岸缓冲带。
2 结果与讨论
2.1 模型可靠性
利用2015年5月至2017年9月的径流、总磷监测数据对模型进行率定,利用2019年12月至2021年12月的径流、总磷监测数据以及2021 年9 月至12 月的吸附态磷、溶解态磷监测数据对模型进行验证,率定结果如图4所示。结果表明,率定期和验证期内径流的NSE和R2均大于0.5,PBIAS均在±25%范围内,说明模拟效果较好。模拟效率方面,研究区共划分为9 635个30 m×30 m的栅格,模拟一次平均耗时4.196 s,率定共耗时6.99 h,模型效率较高。
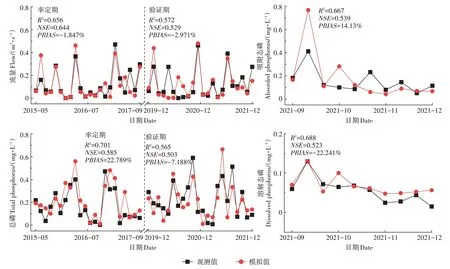
图4 模型率定结果Figure 4 Calibration results of the model
2.2 水土流失型面源污染时空分布规律
2.2.1 空间分布
如图5a 所示,受地形地貌、人类活动等的影响,年均水土流失、吸附态磷和溶解态磷负荷量在空间上分布差异明显。研究区水土流失量在0~149 t·hm-2·a-1之间,平均流失量为 17.23 t·hm-2·a-1。根据水利部发布的《土壤侵蚀分类分级标准》(SL 190—2007)规定,丘陵红壤区容许的土壤流失量为5 t·hm-2·a-1,研究区超过此限值的区域占流域面积的40.2%。吸附态磷负荷量在0~1.72 kg·hm-2·a-1之间,平均值为1.22 kg·hm-2·a-1,溶解态磷负荷量在 0~1.61 kg·hm-2·a-1之间,平均值为0.56 kg·hm-2·a-1。水土流失、吸附态磷和溶解态磷的入河量较负荷量有所下降,分别为9 032.2 t·a-1、601.3 kg·a-1和 541.7 kg·a-1,分别占负荷量的54.32%、50.87%和72.99%。水土流失和吸附态磷的入河系数随着入河距离的增大而减小,因此水土流失和吸附态磷入河量的热点区域主要分布于河道两侧。由于水塘、植被过滤带对溶解态磷的拦截作用有限,随入河距离的增大溶解态磷的入河系数并未显著减小。
此外,将栅格尺度的数据进行加和平均,升尺度至集水区尺度,在集水区的空间尺度上计算了水土流失、吸附态磷、溶解态磷的负荷量、入河量和入河系数(图5b)。
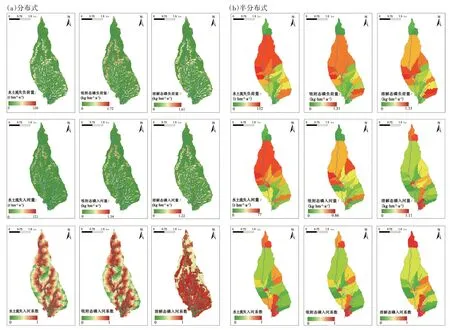
图5 水土流失、吸附态磷、溶解态磷的产生和入河空间分布情况Figure 5 Spatial distribution of production and inflow of and soil erosion,adsorbed phosphorus and dissolved phosphorus
由于林地和坡耕地多集中于中上游流域,因此水土流失和吸附态磷的关键源区多位于中上游的集水区。溶解态磷则主要由水田密集的下游集水区贡献。中上游流域河网稀疏,入河距离较长,入河系数较河网密集的下游流域小。
基于分布式的空间分布可以在栅格尺度上识别负荷量与入河量的热点区域,进而基于栅格尺度的水土流失、面源污染入河量、土壤磷含量等图层,精准识别防控措施的最佳实施位置,为水土流失型面源污染的防控提供依据。尽管基于半分布式的建模方法能大致得出水土流失、吸附态磷、溶解态磷的分布规律,并在集水区尺度上识别面源污染关键源区[24-26],但集水区尺度的结果难以进一步空间降尺度,因此对防控措施指导意义较差。对比分布式与半分布式入河系数的空间分布,分布式模型揭示出栅格入河系数与其入河距离呈负相关关系,但半分布式模型无法得出这一规律,难以为精细化的关键源区识别及防控措施实施提供依据。
表2 为不同土地利用类型下吸附态磷、溶解态磷和水土流失的负荷情况。林地、水田、坡耕地的年均水土流失负荷分别为30.204、9.529 t·hm-2和 15.111 t·hm-2,呈现林地>坡耕地>水田的趋势。林地面积占36.37%,水土流失量占比却高达62.83%,主要是因为林地大多集中于高程差较大的上游流域,此处坡度因子较大,更容易发生水土流失。而面积占比为23.37%和28.26%的水田和坡耕地的水土流失量则分别占比为12.74%和24.42%。春夏季水田和坡耕地施肥使土壤含磷量较林地高,因此水田和坡耕地吸附态磷的占比较其水土流失的占比有所上升。溶解态磷负荷主要受土壤含磷量的影响,因此呈现坡耕地>水田>林地的趋势。

表2 不同土地利用类型下水土流失、吸附态磷、溶解态磷负荷情况Table 2 Distribution of sediment,adsorbed phosphorus and dissolved phosphorus in different land uses
表3 为不同坡度下吸附态磷、溶解态磷和水土流失的负荷情况。结果表明,面积占比为27.71%的陡坡地(坡度>20°)水土流失占比达到了43.80%;相比之下,面积占比为49.13%、坡度<10°的土地水土流失占比却只有26.04%。由于水田和坡耕地大多分布在坡度<10°的土地上,土壤磷含量较高,因此坡度<10°的土地吸附态磷占比达29.88%,溶解态磷占比达54.91%。

表3 不同坡度泥沙、吸附态磷、溶解态磷负荷情况Table 3 Distribution of sediment,adsorbed phosphorus and dissolved phosphorus in different slopes
2.2.2 时间分布
图6为吸附态磷和溶解态磷浓度(图6a)、入河系数(图6b)及其与降雨(图6c)、侵蚀性降雨(>12 mm,图6d)相关性的月际时间变化。结果表明,河道吸附态磷、溶解态磷及其入河系数春夏季节较秋冬季节高,且与侵蚀性降雨相关性较强,其中吸附态磷与侵蚀性降雨的相关性要略高于溶解态磷,在4 月至8 月间,吸附态磷与侵蚀性降雨的相关性在0.4以上,溶解态磷与侵蚀性降雨的相关性在0.3 以上。2 月和3 月水土流失量、流量与侵蚀性降雨的相关性较高,但是吸附态磷、溶解态磷与侵蚀性降雨的相关性很低,主要是因为菁林溪流域的耕种、施肥从4月开始,2月和3 月土壤磷含量较低,导致了磷与侵蚀性降雨之间的低相关性。此外,溶解态磷与吸附态磷入河系数的变化趋势与侵蚀性降雨变化趋势基本一致,相关性在0.3~0.8之间。溶解态磷的入河系数在0.6~0.9之间波动,而吸附态磷的入河系数在0.2~0.6 之间波动,这是因为水塘和植被的拦截能力有限,在面源污染量较少(即侵蚀性降雨量低)时能拦截绝大部分的传输量,而当面源污染较多(即侵蚀性降雨量高)时只能拦截部分传输量,因此侵蚀性降雨量低时吸附态磷和溶解态磷的入河系数较低,而侵蚀性降雨量高时二者的入河系数较高。吸附态磷、溶解态磷及其入河系数与降雨量的相关性较侵蚀性降雨量的相关性低,这主要是因为降雨量较低时,几乎不产生地表径流与水土流失,此时水土流失与非点源磷和降雨量之间无显著关系。

图6 吸附态磷、溶解态磷浓度和入河系数的变化情况以及各指标与非侵蚀性和侵蚀性降雨的相关性分析Figure 6 Concentration and introduced ration changes of adsorbed phosphorus and dissolved phosphorus and correlation analysis between each index and non-erosive/erosive rainfall
2.3 防控措施效果评估
情景2 至情景4 措施实施的空间位置如图7 所示,5 种情景对吸附态磷、溶解态磷和水土流失量的削减情况如表4 所示。在情景2 中,将水土流失强度前30% 的坡耕地进行退耕还林(占流域面积的8.48%),由于坡耕地水土流失占比仅为24.42%,退耕还林措施仅削减了4.78%的水土流失量。而退耕还林措施对面源污染的治理效果较好,分别削减了9.32%的吸附态磷和6.01%的溶解态磷。在情景3中,对土壤磷含量前30%的坡耕地/水田(占流域面积的15.49%)化肥减量50%,分别有17.97%的吸附态磷和20.81%的溶解态磷被削减。在情景4 中,对坡度大于10°的坡耕地(占流域面积的13.61%)进行坡改梯,梯田坡度较坡耕地小,对水土流失、径流、污染物的截留效果更好,分别削减了8.08%的水土流失量、9.03%的吸附态磷和2.37%的溶解态磷。情景5 中,在总磷入河量前30%的滨岸栅格设置了30 m 滨岸缓冲带,经过上游节点的层层传输,滨岸入河栅格的水土流失及面源污染的量最大,在此处布设缓冲带对水土流失及面源污染的削减效果最好。结果表明,情景5 能分别削减26.22%、22.97%、25.01%的吸附态磷、溶解态磷及水土流失。

图7 措施实施位置识别Figure 7 Identification of implementation position of measures
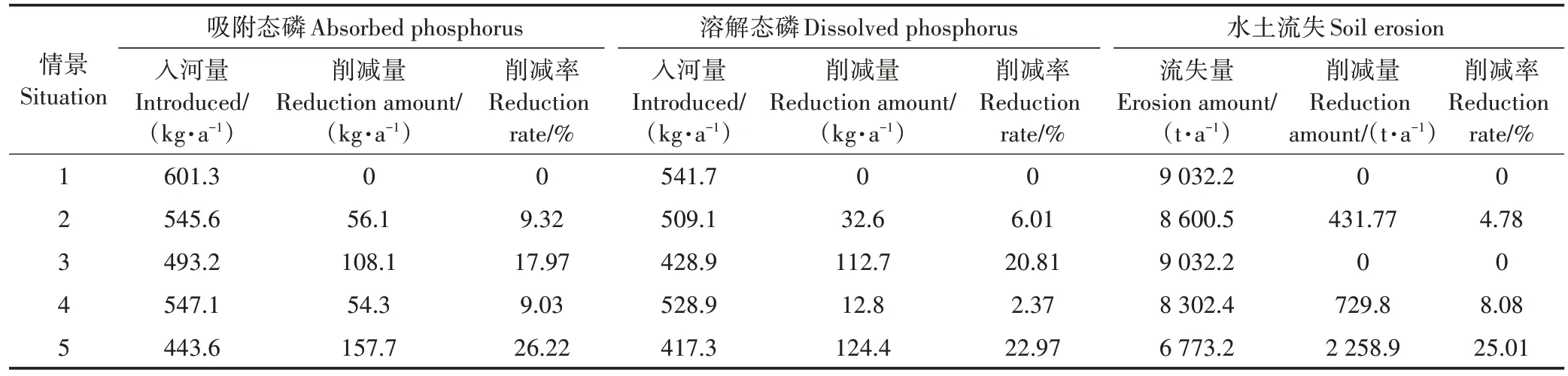
表4 措施削减效果Table 4 Reducing effect of measures
分布式模拟的思路解决了传统水保措施效果评估方法的诸多不足。LI 等[27]基于SWAT 模型,发现在坡度>25°的坡耕地上实施退耕还林能降低59.53%的总磷负荷,但是基于半分布式模型进行效果评估仅能模拟每个集水区的削减效果,并且忽略了水土流失和污染物在传输过程中的损失。水土流失和污染物在传输过程中由于自然沉降和植被拦截会遗留在田块上,在之后的降雨事件中会被二次冲刷[28],因此半分布式模型可能会对退耕还林的减污效果有所高估,并且难以精准定位退耕还林的最佳实施位置。分布式模型则能模拟水塘、植被缓冲带等地表景观对水土流失、污染物的截留,以最终入河量削减为评估目标,更加真实可靠。另外,分布式模型能在栅格尺度上模拟水土流失和污染物的负荷量、入河量、土壤磷含量等信息,为识别退耕还林、化肥减量、坡改梯、滨岸缓冲带等措施的最佳实施位置提供依据。例如在设置滨岸缓冲带时,半分布式模型无法识别面源污染入河量最高的滨岸栅格,在所有滨岸栅格设置滨岸缓冲带则成本过高,随机设置滨岸缓冲带则效果不如设置在关键滨岸栅格,因此分布式模型比半分布式模型对管理措施的实施更具指导意义。
3 结论
(1)本研究针对半分布式模型的局限性,考虑了降雨径流、土壤侵蚀、田块流失、水塘拦截、植被过滤、泥沙沉降、河道磷循环等分布式水土流失型面源污染关键过程,构建了分布式水土流失型面源污染模型,模型模拟精度较高;并基于反向递归与哈希表提出了高效汇流算法,破解了分布式模拟面临的计算瓶颈问题。
(2)三峡库区菁林溪流域内水土流失、吸附态磷和溶解态磷的负荷强度分别为17.23 t·hm-2、1.22 kg·hm-2和 0.56 kg·hm-2,其中分别有 54.32%、50.87% 和72.99%的水土流失、吸附态磷和溶解态磷最终进入河道。
(3)丘陵山区水土流失面源防控应重点关注坡耕地影响,林地、水田、坡耕地的吸附态磷流失强度分别为 1.911、1.179、2.192 kg·hm-2,溶解态磷流失强度分别为0.604、1.084、1.086 kg·hm-2,面积占比28.26%的坡耕地即贡献了全流域38.91%的溶解态磷和39.45%的吸附态磷。
(4)溶解态磷的入河系数在0.6~0.9 之间波动,吸附态磷的入河系数在0.2~0.6 之间波动,并且二者与降雨量之间呈现较强的相关性。
(5)相对于化肥减量等经典农艺措施,在入河负荷最大的滨岸栅格上设置滨岸缓冲带对丘陵山区面源防控效果更佳,其能分别减少26.22%的吸附态磷和22.97%的溶解态磷的入河量。

