基于坎贝拉度量改进的智能拼图算法

吴娟

（济南工程职业技术学院信息工程学院，山东 济南 250200）

1 引言

数据挖掘技术的进步使得大规模的图像问题得以被解决，例如用计算机解决拼图问题能够实现碎片的还原和图像对象的定位等。好的拼图技术能够在上百以及上千个拼图块中找到最好的匹配。最近有研究[1,2]实现基于图模型解决拼图问题，它用一个节点代表相邻两块的相似度分数。其中，Gallagher[1]提出了一种新的兼容性测量MGC(马氏相似度度量)。Paikin和Tal[2]提出了对于缺失拼图块的解决方案。Kosiba等人[3]根据拼图块的颜色相似性进行匹配。Yao等人[4]根据拼图分类策略来组装拼图。Nielson等人[5]采用分而治之的策略，通过对可能相互连接的碎片进行分组组装。还有一些研究[6-10]不考虑碎片的形状信息，主要考虑碎片的内容来解决方形拼图问题。这些方法一般都是首先计算相邻块的相似度，然后利用贪婪算法组装拼图。

目前大多数拼图算法侧重于计算拼图块之间的边缘相似度，即测量拼图块边缘的像素之间的兼容性，但不是检查所有边缘像素。虽然机器学习能够利用像素级分析边缘相似度，但是不容易实现。通过考虑拼图块之间的边缘相似度，本文提出一种改进的拼图算法来解决未知方向、未知位置的拼图。将计算边缘相似度的坎贝拉距离算法与MGC算法结合，使得还原图像更准确。

2 算法与改进

MGC（马氏相似度度量）是一种能够较好还原图片的相似度测量算法。早期的SSD算法仅仅比较RGB值的差异，而MGC通过比较颜色梯度，实现了较高的准确率。还原算法有贪婪算法、遗传算法等，其中基于最小生成树的还原过程能够还原出较准确的图片。

2.1 MGC度量（马氏相似度度量）

MGC通过考虑边缘相似度，使度量更准确，不但计算相邻块之间颜色梯度的协方差，而且将马氏距离应用其中。

拼图块xj在xi的右侧，计算相似度评分ELR(xi,xj)时，首先表示出拼图块xi右边缘颜色梯度变化的向量，定义一个P*3的矩阵。其中，GiL表示拼图块xi右侧边界梯度变化。

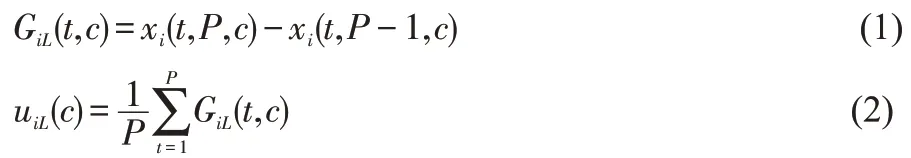
uiL为拼图块xi右边缘的平均分布。t为行数，c为颜色通道。

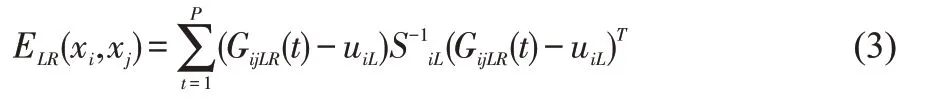
其中Si是图像块xi右边缘颜色梯度的一个3*3的协方差矩阵。ELR(xi,xj)为xi到xj的相似度度量。

GijLR(t)为拼图块xi右边缘到拼图块xj左边缘的梯度变化。

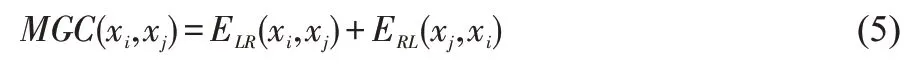
公式(5)为修正公式。ELR(xi,xj)是拼图块xi到拼图块xj的马氏距离，ERL(xj,xi)是拼图块xj到拼图块xi的马氏距离。MGC(xi,xj)为两个拼图块之间马氏距离的加权值。

2.2 采用Kruskal算法还原图像

每个拼图块是一个顶点，相邻拼图块之间的MGC为边的权重，构成矩阵E。

（1）找出E中代价最小的边emin并将其从MGC矩阵中移除。如果emin的顶点位于同一个森林，则为了避免环路的形成，将emin舍弃。如果在合并森林时，两块拼图占据相同的位置，即发生了冲突，则舍弃emin。如果emin符合要求通过检测，则将其加入森林；否则继续在剩余边里选取权重最小的，重复以上步骤。

（2）将生成的最小生成树进行剪枝，剪枝时把最大部分留在矩形内。

（3）将矩形中剩余部分进行填充。

2.3 坎贝拉距离计算

坎贝拉距离(Canberra距离)算法最早是由Lance和Williams提出的。它是相似度分析中一种度量距离的常用方法。好的度量方法对于碎片之间的微小差异是很敏感的，当图片中出现大量相似物时，利用MGC方法进行组装拼图的准确率会降低。因此本文将坎贝拉距离算法应用于拼图中。

提取相邻块边缘某一行（列）的RGB特征。将相邻拼图块标记为pi、pj，若pi是块i的上边缘，则pj是块j的下边缘，则pi(h,Q,c)为拼图块pi在第h位置第c通道最左侧边界的颜色梯度，则pj(h,l,c)为拼图块pj在第h位置第c通道最左侧边界的颜色梯度。然后通过计算相邻块边缘对应向量之间的坎贝拉距离，从而得到相邻块之间的相似度度量：

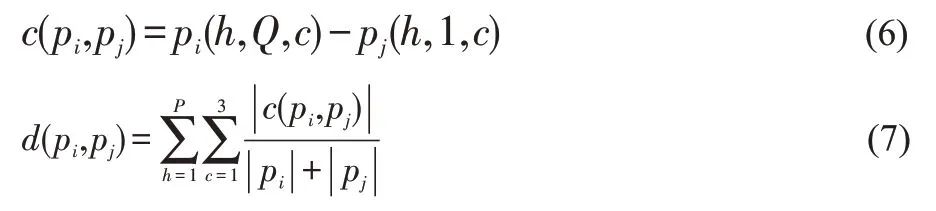
其中d(pi,pj)为相邻两块拼图块的坎贝拉距离。式中d(pi,pj)越小，说明pi，pj接近程度越大，否则说明pi，pj接近程度越小。

2.3.1 Canberra与MGC结合方式一

当有大量相似物时，单纯的MGC算法准确率不高，因此本文提出将Canberra与MGC结合的度量方式。新的度量方式能够增加碎片之间的差别。

公式（8）（9）中a，b值大小不同时，进行正确匹配的拼图块的数量不同，运行时间也会不同。

在对a∈{0.4,0.5,0.6,0.7}时进行对比分析，发现当a=0.7时正确匹配的拼图块的数量最多，效果最好。将此方法标记为Can1。

Can1算法在不同a取值时，正确匹配的拼图块的数量对比如图1所示。

从图1中可以看出，当a=0.7，b=0.3时正确匹配的拼图块的数量最多。因此后续的实验中取a=0.7，b=0.3。

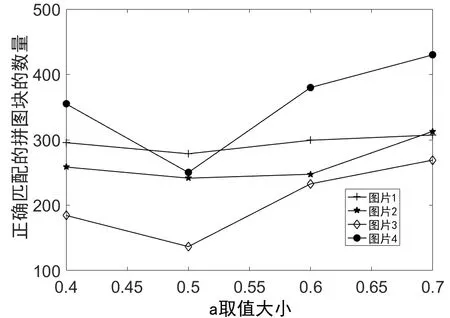
图1 a值不同时，不同图片匹配正确的拼图块数量对比

2.3.2 Canberra与MGC结合方式二

将Canberra距离与MGC距离结合测量两个拼图块之间的相似度公式如下所示：

公式（10）中r是一个可以设置的自由参数，对r∈{1/2,1/4,1/8,1/16}进行对比分析，发现当r=1/4时效果最好。将次方法标记为Can2。

r值大小不同时，Can2算法进行正确匹配的拼图块的数量对比如图2所示。

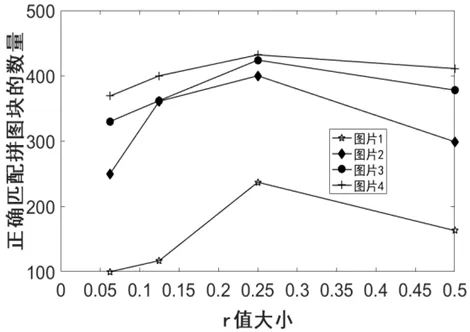
图2 r值不同时，不同图片匹配正确的拼图块数量对比

从图2中可以看出当r=1/8开始正确匹配的拼图块数量明显下降，r=1/4，即r=0.25时正确匹配的拼图块数量最多。因此后续的实验中取r=1/4。

类似于Gallagher[4]，我们假定N为相似度矩阵，则N(pi,pj)是拼图块pi和pj的相似度评分，设P为所有拼图块的集合，则归一化矩阵N"定义如下：

由于不需要将拼图块与自身相比较，因此对角线上的项不需要考虑。这一规范化提高了拼图的准确率。

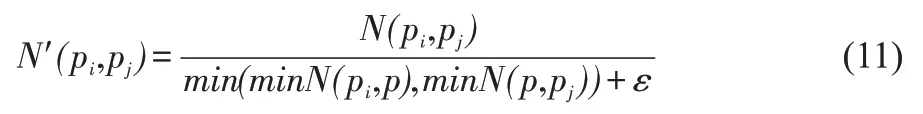
2.3.3确定整体拼接策略

贪婪算法即一步一步地构建问题的最优解决方案。其中每一步只需考虑眼前的最佳选择，即我们希望通过局部最优到达全局最优。

（1）确定判断阈值函数值。

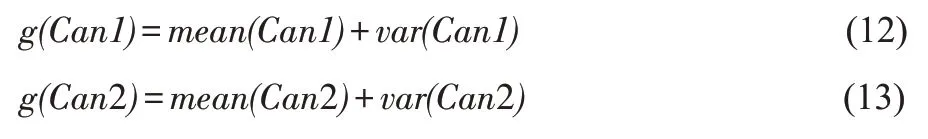
其中mean(Can1)、mean(Can2)是Can1和Can2的均值，var(Can1)、var(Can2)是Can1和Can2的方差。

（2）将计算的所有块与块、每种块与块之间的16种组合的g(Can1)、g(Can2)的值，选择值最小的值作为正确的拼接。

（3）将上一次结果与剩余块拼接，防止出现重叠。

图3中拼接发生冲突，因此合并这两个森林后的结果将被丢弃。图4中拼接未发生重叠，因此为正确拼接。

图3 拼接发生冲突

图4 成功拼接

（4）如果拼接之后的结果图片的维度超过原图像维度，需要剪枝。

（5）剪枝之后，将剩余空缺较小的部分重新填充完毕。

3 实验结果及分析

3.1 三种算法对于无噪声图片效果对比

本文将网络图像库以及实验拍摄的一些图片分为14组，分别利用Can1算法、Can2算法和MGC算法进行测试，将每张图片划分为432块，每块28×28像素，实验环境选择Win10 64位操作系统，MatlabR2021a编程实现。实验结果如表1所示。本文在图5中展示6张图片采用两种算法来重建图像的匹配图。

图5 三种算法准确率对比

从表1中可以发现，在所测试的14组图片中，使用本文两种算法，拼图块进行匹配的准确率都有所提高。Can2相对于大多数图片，都能得到较高的准确率。超过64%的图片有高达90%以上的准确率。对于背景单一图片Can2算法仍能达到80%左右的准确率，而此时MGC只能达到60%左右的准确率。Can1相对于某些图片虽然也起到了微调的作用，准确率也有所提高，但相比于Can2效果要差。

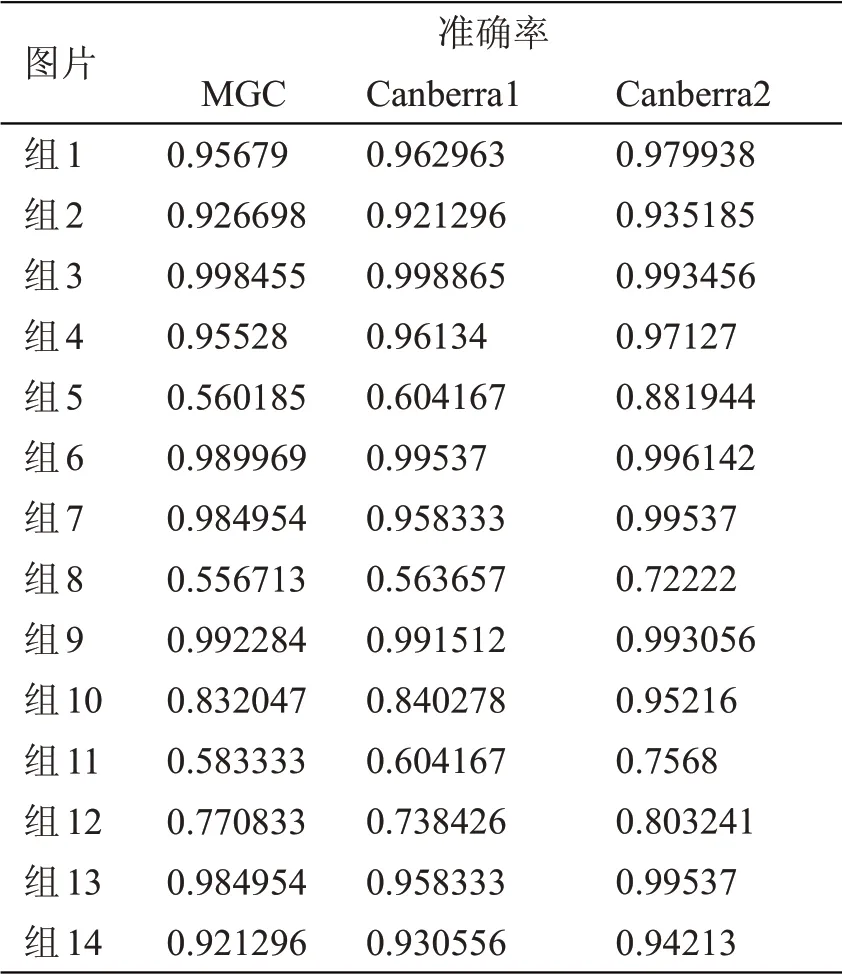
表1 三种算法准确率对比

图5中将三种算法完成图作对比，左为利用MGC还原后的图像，中间为利用Can1还原后的图像，右为利用Can2还原后的图像。从图5中可以看出，对于相似度小的图像，三种方法均能得到比较完整的还原图像。而对于背景单一相似物多的图片，利用坎贝拉距离还原后的图像能够减少图片乱码的出现。

本文算法相比于MGC算法准确率有所提高，是因为对于背景图片单一、有大量相似物时，相似块之间，利用坎贝拉距离算法计算出的矩阵减少了相等值的出现，而利用MGC算法计算出的马氏距离会有比较多的相同情况，因此还原后的图像会有差异。对于背景复杂的图像，Can2算法和MGC算法都能区分出拼图块之间的差异，因此还原此种图像效果较好。

3.2 噪声干扰下两种算法对比

拼图问题为广泛的实际应用提供了可能的解决方案，如考古遗物的重组，被破坏文件的复原。在这些应用中，现实图像总存在大量噪声。过去的文献中，解决拼图问题往往假定图像是完美的，受到噪声影响后，其准确率会有明显变化，比如MGC算法。本文对于受到噪声干扰的图像进行实验预估。首先对14组图片添加噪声，然后对两种算法的准确率进行对比。每张图片均加入密度为0.05的椒盐噪声及均值为0、方差为0.01的高斯噪声，观察其准确率。

图6，图7中结果可以看出，对于14组测试图片中，MGC算法对于个别背景单一的图片，加入噪声后其准确率会有所提高，而对于背景复杂的图片其准确率会有所下降。而Can2准确率始终比MGC准确率高，表现出很好的鲁棒性，优于MGC还原图像的算法。

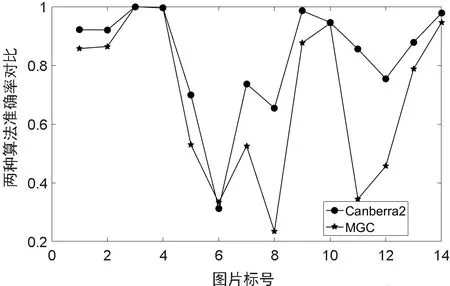
图6 高斯噪声影响下两种算法的准确率

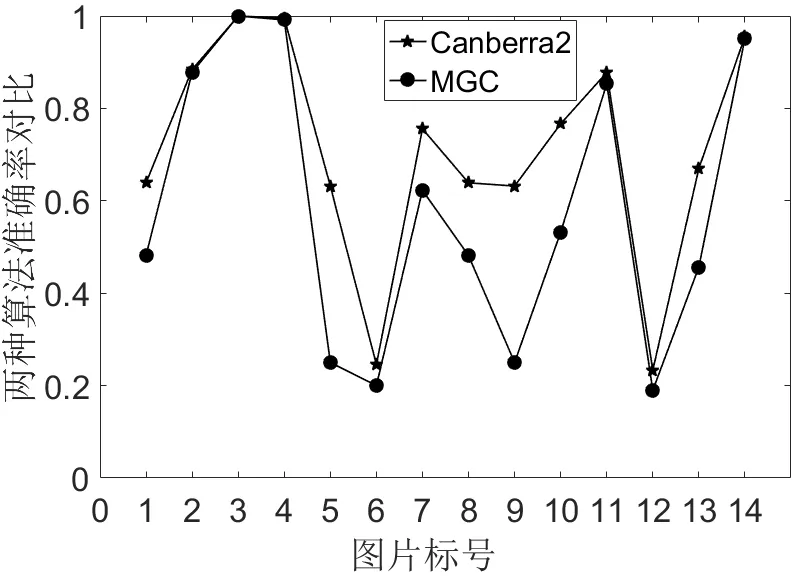
图7 椒盐噪声影响下的两种算法的准确率

3.3 设置图片缺损

重建图像的另外一个难题是当图片不完整时，是否还能达到很高的准确率。随机设置黑块制造不完整性，对第一组所有图片随机进行涂黑。

将Can1算法与MGC算法作对比，从图8中可以看出，MGC的准确率低于Can1的准确率，MGC的准确率只有0.6。

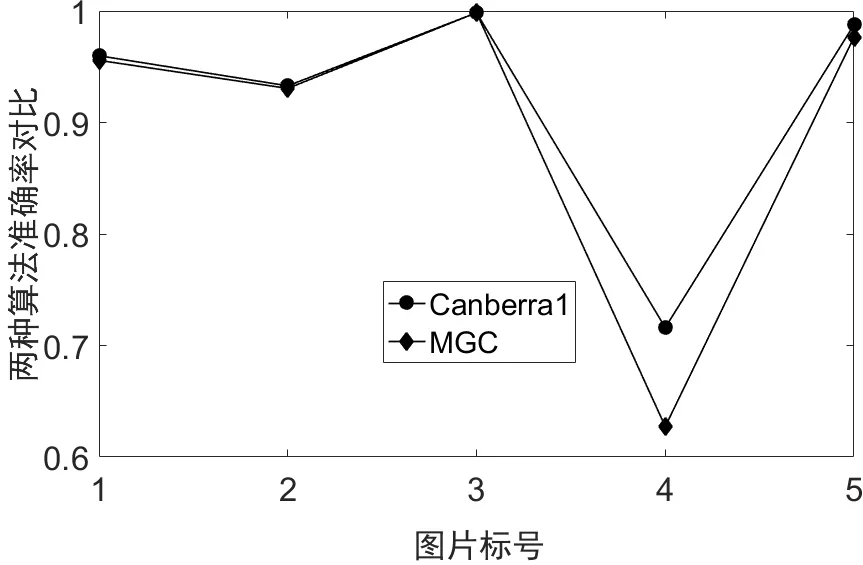
图8 第一组图片加黑块后的准确率

4 结语

本文提出了一种新颖的拼图算法，通过坎贝拉距离计算相邻块边缘的颜色梯度，根据坎贝拉算法与MGC算法结合得到的距离对相邻拼图块的相似度进行评分，重建图像时本文先将结果值进行加权，然后还原图像。

坎贝拉测量算法实验结果表明，本文中的算法对于所测试图片有较高的准确率，当有噪声干扰时，Can2算法相比于MGC算法有较高的准确率，当图片设置缺损时，虽然两种算法相对于之前完整的图像准确率有所降低，但是Can1算法的准确率高于MGC的准确率。后续的工作中，将进一步优化算法，提高算法的鲁棒性和准确率。