基于OBE理念的Matlab工程基础案例实践

尹宗明,付玉萍,何晓芬,张 宁,高榆岚

(贵州工程应用技术学院机械工程学院，毕节 551700)

1 OBE教学理念

OBE(Outcomes-based Education)，即基于学习产出的教育模式，最早由美国学者Spady提出，他在《基于产出的教育模式：争议与答案》一书中对该理念进行了深入剖析[1]。以学生为本和以学习产出为导向是OBE理念的重要思想。与传统按照课本目录章节进行教学不同，它将焦点集中在学生受教育后的效果上[2]，更加突出学生受教育后自身能力获得。基于OBE设计的教学内容以学生学到了什么，在学习过程中培养了什么能力，通过学习最终具备了什么能力为目标，采用的教学方法和实施的教学过程对提高学生的学习积极性具有显著的作用。

2 相关研究现状

Matlab在数据分析、深度学习、无线通信、图像处理与计算机视觉、量化金融与风险管理、信号处理、机器人，控制系统等领域有着广泛的应用[3]，因此众多高等院校都开设了Matlab这门课程。针对Matlab课程的教学研究一直以来都是教学改革的热点之一，取得来很多优秀的研究成果。例如文献[4]针对新工科背景下《Matlab与控制系统仿真》翻转教学进行了研究；文献[5]基于Matlab与自动控制原理的稳定性分析进行了教学研究；文献[6]针对大学物理理论教学与Matlab/Simulink仿真技术结合的教学进行了探讨；文献[7]研究了Matlab软件在机械原理课程OBE教学改革中的应用。这些研究对Matlab的教学改革起到了积极的作用，但鲜有涉及基于OBE理念的Matlab工程基础教学研究问题，因此该问题的研究对提高Matlab工程基础这门课的教学质量具有重要的意义。

3 传统Matlab工程基础课程教学中存在的问题

Matlab工程基础包括数值计算和模拟仿真两大部分，涉及到众多数学理论课程(高等数学、线性代数、复变函数与积分变换、自动原理、机械设计等)和专业课程(机械工程控制基础、机械原理、机械优化设计等)的知识，是一门应用性强并与实践紧密结合的应用型课程。通过学习该门课程，学生应具备利用Matlab高性能数值计算能力和可视化功能平台仿真去解决机电工程设计分析过程中遇到的各种数学计算和仿真问题的能力。Matlab工程基础课程教学中存在的问题一方面体现在目前课堂教学是本科教育主要的教学方式之一，强调理论学习的完备性，忽略了学生工程实践性的培养，因此造成了学生在学习该门课程的过程中觉得课程枯燥无味、无明显目的性的困惑[1]。另一方面，应用型本科高校学生数学基础相对较差，在讲授该门课程过程中涉及到较难较生的数学知识时，学生很难理解，进而导致学生记不住相关知识点[8]。久而久之，学生便失去了学习该课程的兴趣。

4 结合实际应用、弱化传统课堂教学的课程改革

针对Matlab传统课堂教学中存在的问题和Matlab工程基础课程的实践性特点，受OBE教学理念的启发，我们提出了“结合实际应用、弱化传统课堂教学”的教学观点。弱化传统课堂教学并非是放弃课堂教学，而是缩短教师课堂教学学时，增加实践学时。以48学时为例，教师首先应在30学时内将Matlab工程基础课程的知识点全部讲解完，然后剩余的18学时全部用于Matlab的工程实践教学。在实践教学中，引入4～6个与本专业相关的实际应用案例作为教学材料。例如针对机械电子工程专业的学生，可引入连杆机构的运动设计分析，凸轮机构运动分析和设计计算，齿轮、蜗杆和螺旋传动的设计计算，机械联接设计计算，优化设计分析和曲线拟合，控制系统的稳定性分析与设计仿真等。根据这些实际的应用案例，将学生分为3～5人的小组，小组学生再根据组内每名同学擅长的内容进行任务分解，提前通过网络(如百度、Google)、书籍(专业教材)和数据库中的相关学术论文查询实验应用案例所涉及的知识内容，做好实验准备。实验时，小组内同学根据自己的特长选择相应的模块进行计算或仿真，例如同学A负责用Matlab软件进行非线性方程组的求解，同学B负责曲线拟合，同学C负责Simulink仿真模型的搭建和参数设置，同学D负责仿真结果的数据可视化处理，同学E负责实验报告的整理。实验过程中教师全程现场指导，现场有问题，现场解决。实验完成后，教师针对学生在实验过程中存在的问题进行统计，然后针对存在的问题进行重点分析讲解，让学生彻底理解Matlab在工程实践中的完整应用流程，以达到以学生为本和以学习产出为导向的教学效果。

5 一个教学案例

受OBE教学理念的启发，结合本文提出的“结合实际应用、弱化传统课堂教学”的观点，本节将控制领域科技前沿热点问题的分析、计算、仿真融入到机械电子工程专业Matlab工程基础这门课的教学中，让学生完整地实现Matlab在控制实践中的应用，以激发学生学习该门课程的兴趣。

众所周知，在我们的日常生活中，延迟现象随处可见，如物质传递、信息传输和能量交换等。延迟现象在控制系统中主要体现为：系统将来的变化趋势除了和当前的系统状态相关，还与系统过去一段时间内的状态有关。表现出这种现象的控制系统被人们称为延迟系统。大多数动态系统，比如过程控制系统、生物系统、网络控制系统和人口周期模型系统等，都存在时延问题。时延的存在会导致系统的控制性能变差，甚至于不稳定。另外，时滞的存在使得对系统的理论分析和工程应用都增加了特殊的难度。因此对延迟控制系统的研究具有重要的实践意义[9]。

针对一个经典的线性时不变延迟系统数例(该数例在时滞系统的研究中被大量使用[9])，引导学生思考如何用Matlab对该系统进行分析计算以及仿真验证，以激发学生的学习兴趣。考虑如下的线性时滞系统:

(1)

第一步：将学生分成3～5人一组，以小组为单位进行资料查询，例如查询《线性系统理论》，掌握系统特征方程知识点、Matlab非线性方程组的求解等。

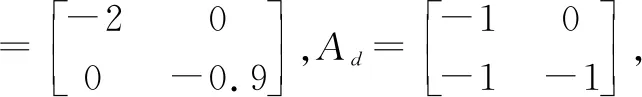
(2)

上式成立只需s+0.9+e-hs=0，令s=jw，代入该式得

jw+0.9+e-hjw=0

(3)

可以看出，方程(3)无法直接求解。根据欧拉公式，即e-jx=cos(x)+jsin(x)，进而

e-jhw=cos(-hw)+jsin(-hw)=cos(hw)-jsin(hw)

(4)

结合(3)和(4)得

j(w-sin(hw))+0.9+cos(hw)=0

(5)

进一步有

(6)

第二步：每个小组根据Matlab工程基础知识，编写程序对(6)进行求解。

通过Matlab中非线性方程组的求解函数[x, fun]=fsolve(fun,x0)进行求解。针对方程(6)，令x(1)=w，x(2)=h，求解初值x0=[2;1.2]，详细的Matlab求解代码如图1。

通过Matlab编程求解，我们可以得到w=0.4359，h=6.17s。结合机械工程控制基础知识，可知系统(1)的临界稳定点为h=6.17s。

第三步：各小组在Matlab软件中的Simulink仿真平台搭建系统(1)的仿真模型(如图2)，验证求得结果。

设系统初始值为[1;1]，采样步长为0.01，h=6.1s时(理论上，此时系统是稳定的)，仿真结果如图3。

h=6.2s时(理论上，此时系统是不稳定的)，仿真结果如图4。

根据前面理论计算的系统临界稳定点为h=6.17s，图3为系统在h=6.1s时的状态响应，可以看到随着时间推移，系统状态演变逐渐趋近于0，这说明系统是稳定的。图4为系统在h=6.2s时的状态响应，可以看到随着时间推移，系统状态是发散的，这说明系统是不稳定的。图3和图4的仿真结果验证了系统临界稳定点为h=6.17s这一理论结果。

第四步：在学生实验过程中，根据学生在运用Matlab进行非线性方程组求解、仿真模型搭建、参数设置、图形处理和仿真结果分析等方面遇到的问题进行实时指导和评分，达到现场有问题，现场解决的效果。

上述各个步骤相互独立，又相辅相成，小组内同学可根据自己的特长选择相应的模块进行计算或仿真。

该仿真教学案例每个学生都能参与，培养了学生的团队协作能力，激发了学生学习该门课程的兴趣。

该仿真案例结合OBE教学理念，通过分组实验和现场教学讲解，实现了如下的教学目标：

A. 学生掌握了Matlab的操作基础、Matlab中的矩阵和数组知识点；B. 学生理解了Matlab数据可视化的优点；C. 学生具备了线性和非线性方程组的Matlab求解能力；D. 学生掌握了Matlab软件分析实际控制系统的稳定性的方法；E.学生具备了使用Matlab分析工程设计的能力。

6 结语

基于OBE教学理念，本文提出了“结合实际应用、弱化传统课堂教学”的教学观点，并将控制领域科技前沿热点问题的分析、计算、仿真融入到机械电子工程专业Matlab工程基础这门课的教学中。本文给出的基于OBE理念的Matlab工程基础案例，可以使学生学生掌握Matlab工程基础这门课程中的代数方程求解、Simulink平台仿真和数据可视化等众多知识点；使学生理解Matlab具有集算法开发、数据可视化、数据分析、数值计算以及模拟仿真于一体的强大功能。该仿真教学案例的实施，不仅使学生理解了数值计算和计算机仿真软件在机械控制中的应用，而且还能增强学生理解和运用专业知识的能力，提高学生的学习兴趣和创新实践能力，达到以学习产出导向为目标的效果。