新型电力系统的频率响应模型综述及展望
刘翔宇,李晓明,朱介北,段绘策,俞露杰,于腾凯
(1. 国网河北省电力有限公司电力科学研究院,石家庄050021; 2. 华北电力大学电气与电子工程学院,河北 保定0710002;3. 天津大学电气自动化与信息工程学院,天津300072)
0 引言
在我国“双碳”目标的驱使下,风力发电和光伏发电将迎来新的跨越式发展。据预测2030年新能源装机容量将新增1.07~1.27 TW,总量将达到1.6~1.8 TW[1]。然而,新能源发电固有的波动性、随机性和并网设备的电力电子化等新特征,对未来电网的电能质量和运行调度产生了明显影响,一定程度地限制了电网新能源整体消纳水平。同时“高比例可再生能源”和“高比例电力电子设备”两大电网新特性,导致系统惯性和旋转备用容量明显下降[2]。在短路故障、发电机切机和负荷突增等工况下,电网的频率变化率和最大偏离量将显著增加,甚至会触发低频减载(under-frequency load shedding, UFLS)动作而引起断电事故[3],威胁电力系统的安全稳定运行[4 - 6]。
2015年9月19日,世界上容量最大、输电距离最长的锦苏±800 kV特高压直流工程发生双极闭锁事件,大幅功率缺额致使华东电网频率降至历史最低值49.56 Hz[7 - 9]。2019年8月9日,英国发生的大断电事故[10 - 12]是近年来因新能源导致的影响范围最大的一次停电事故,造成的经济损失和不利社会影响不可估量。该断电事故是由于新能源大规模发展导致系统惯量过低,发生电网故障时,频率快速下跌,触发了低频减载保护。由此可见,对电网频率响应实现预判的建模和分析方法尤为重要。另外,我国实现“西电东送”的大规模交直流互联电网已逐步形成,采用广域测量系统(wide area measurement system, WAMS)来分析频率时空分布特性的频率响应模型,对保障大型电力系统频率安全运行具有重要作用[13]。
传统电网频率响应模型,往往只针对同步电机而忽略新能源接入电网的场景。现有的新能源电站,新能源电源通常采用最大功率追踪模式[14],不参与电网调频环节。随着电网调频需求的不断增加,未来越来越多的新能源将附带新型控制策略(例如,虚拟同步机控制),主动参与电网的一次调频和惯性响应。由于新能源大规模并网导致电力系统的频率特性出现显著变化,需建立考虑新能源新型控制的复杂电力系统模型,以精确分析频率响应,优化频率控制策略。同时,电力系统负荷侧通常采用低频减载等频率控制策略,建立电力系统精准频率模型以分析和优化低频减载策略,对保障电力系统频率运行安全具有重要意义。
本文首先描述电网频率模型的构建与预测分析方法,同时从考虑时空分布特性的角度出发,综述基于新型广域量测技术的频率时空分布建模方法,然后重点论述基于频率模型的新能源控制和低频减载优化,最后展望该领域亟须解决的主要问题。
1 电网频率模型构建方法与预测分析
电力系统频率响应模型的构建方法,包括时域仿真法、单机等值法、线性分析法、基于人工智能技术的频率预测方法等,上述4种方法之间是非替代的关系,应用于不同的场所和目的。本节对以上几种方法进行论述和比较。
1.1 基于时域仿真的频率响应模型
时域仿真分析法是应用最早、最普遍的电网频率响应分析方法,涉及了系统各个元件(包括不同电源类型、电网拓扑、负荷以及线性非线性控制环节[15])的时域模型构建与连接,其典型模型结构如图1所示[16],其中ω为发电机转子转速,ωref为转速参考值,Uref为励磁电压参考值,Ef为励磁电压,δ为发电机转子相角,Pm为原动机输出功率。时域模型搭建完成后,可对频率动态响应过程进行具体分析。常见的时域仿真软件包括DIgSILENT PowerFactory、MATLAB、PSS、PSD-BPA、PSASP等[17]。
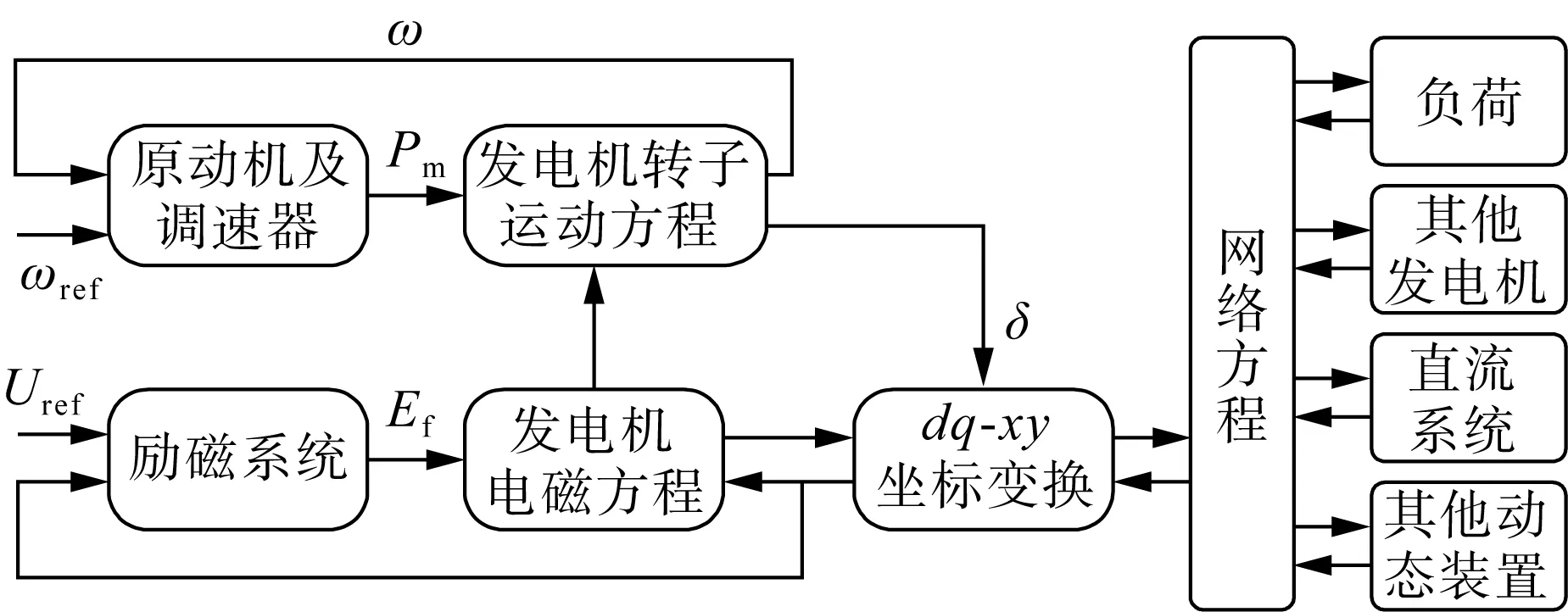
图1 时域仿真模型结构图Fig.1 Structure diagram of time domain simulation model
总体来说,时域仿真法可考虑电力系统详细参数,计算方法成熟且仿真误差小。但是,时域仿真在分析大规模电力系统时,耗时往往较长,较适用于电网规划和事故重现的离线分析,不适用于对时效性要求较强的电网实时调度分析。
1.2 基于单机等值模型法的频率响应模型
为了提高系统频率响应分析速度,提出了更为简化的频率建模方法,主要包括单机等值法和线性化分析法。单机等值法将电力系统简化为单台同步电机,将电网频率视为单台同步机的频率。基于单机等值模型的频率响应建模方法分两类:平均系统频率(average system frequency, ASF)模型[18 - 19]和系统频率响应(system frequency response, SFR)模型[20 - 21]。
ASF模型保留各台发电机的原动机与调速器模型,聚合各台电机的转子运动方程,并对传输线路进行简化。其模型结构如图2所示[18],其中PL为全网总负荷,n为发电机数,Pmn为第n台机组的机械功率,Δω为系统平均转速偏差。
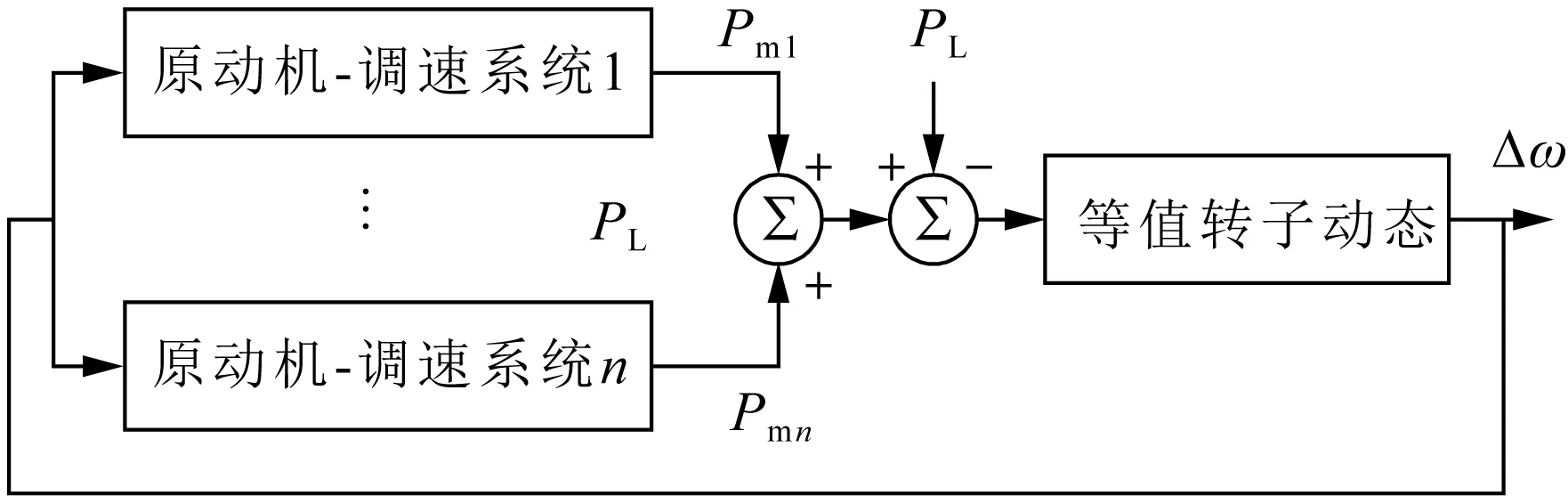
图2 ASF模型示意图Fig.2 Schematic diagram of ASF model
SFR模型在ASF模型的基础上将各发电机组的原动机和调速系统的动态特性进行单机等值,将整个电力系统简化为二阶线性模型[20 - 21]。SFR模型结构进一步降低了系统计算阶数,并具备计算电力系统频率关键特征解析表达式的能力。其架构如图3所示,H为发电机的惯性时间常数,D为发电机的等效阻尼系数,R为调速器的调差系数,TR为原动机的再热时间常数,FH为原动机的高压缸做功比例,Km为与发电机功率因数和备用容量相关的系数,Pm为原动机输出功率,Pe为负荷功率,PSP为发电机增发功率。
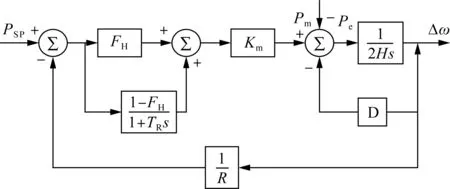
图3 SFR模型示意图Fig.3 Schematic diagram of SFR model
针对以上SFR模型传递函数进行分析计算,可得系统的频率偏差的解析表达式为[20]:
(1)
其中:
(2)
式中ω1为简化计算的中间变量。
由式(1)可知,PSP和Pe在电网频率变化方面的影响类似。大多数频率动态分析场景通常只关注Pe的变化,忽略PSP的变化,故可以进一步简化SFR模型,如图4所示。其中Pd统一为电网中发电或负荷的变化。
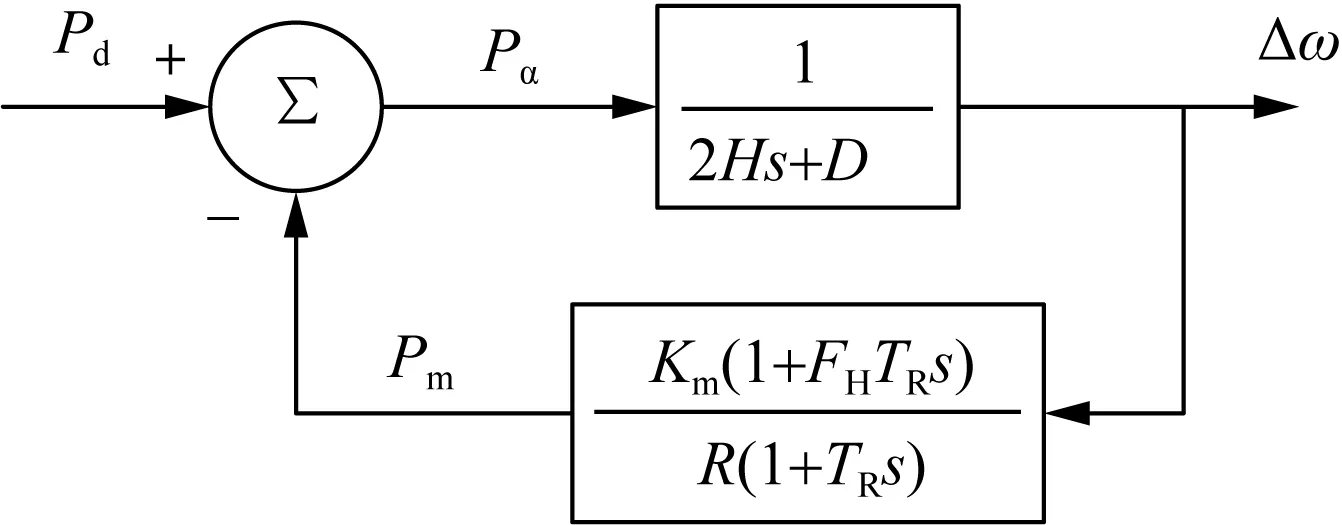
图4 扰动下简化SFR模型示意图Fig.4 Simplified SFR Model with disturbance input
因此,式(1)可以简写为:
(3)
通过拉普拉斯反变换,可求得频率偏差的时域表达式为:
(4)
其中:
(5)
式中ω2为简化计算的中间变量。
在动态频率变化过程中,频率关键特征主要包括:频率稳态偏差值Δω∞、初始频率变化率(rate of change of frequency, ROCOF)和最大频率偏差Δωmax及具体时刻[22],如图5所示。频率稳态值可由式(3)直接计算得到,频率初始变化率、最低值及具体时刻可由式(4)通过计算dω/dt求得。
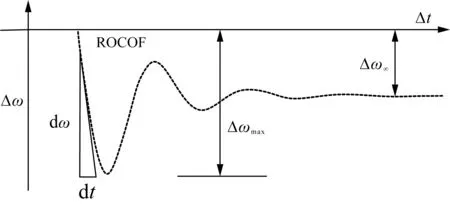
图5 系统频率关键特征值示意图Fig.5 Schematic diagram of key characteristic values of system frequency
单机等值频率模型虽然结构简单,可一定程度地保留电力系统频率的关键解析特性,但无法反映电网频率动态的时空特性细节。
1.3 基于线性化分析法的频率响应模型
线性分析法考虑系统的拓扑结构,对系统中电力元件进行线性简化,建立电力系统频率的时域表达式,获得计算效率较高的频率响应频域模型[23]。文献[24]线性化了发电机原动机-调速器动态方程和转子运动方程等,建立了系统频率的复频域方程,通过反拉普拉斯变化获取了频率动态特征的时域值。文献[25]将系统网络潮流方程描述为一个线性方程组,采用直流潮流法计算电网中机组节点的有功功率变化,并采用简化的发电机模型和静态负荷模型,使用迭代积分方法分析了系统动态频率主要特征。文献[24 - 25]应用在传统电力系统,尚未体现其在新型电力系统场景下的优势。图6展示了基于直流潮流的频率响应模型,其中ωn为第n台发电机转子转速,Pmn为第n台机组的机械功率,δn为第n台发电机的转子相角。
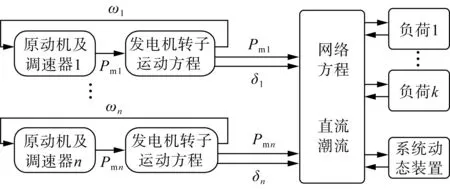
图6 基于直流潮流的频率响应模型Fig.6 Frequency response model based on DC power flow
线性化分析法相比时域仿真模型计算效率显著提高;相比单机等值法进一步考虑了多台发电机的动态方程。但是同样地,基于线性化分析法的频率响应模型无法反映电网频率动态的时空特性。
1.4基于人工智能技术的频率响应建模方法
人工智能算法可有效处理物理模型非线性和复杂的问题,为复杂电力系统频率模型的建立提供新的解决方案。神经网络、粒子群算法、支持向量机、深度学习等人工智能算法应用于互联电力系统的频率在线预测,其基本架构如图7所示。
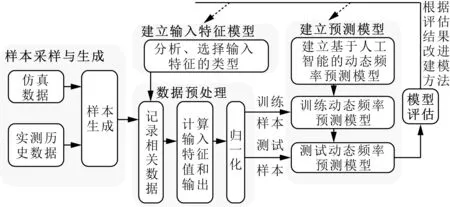
图7 基于人工智能法的频率预测模型框架Fig.7 Frequency prediction model framework based on artificial intelligence method
文献[26]利用人工神经网络,优化了模型频率最低值预测的精确度,包含多个隐含层和高度抽象输入层数据的深度学习算法。相较结构简单的人工神经网络,具有更强的数据特征提取能力,文献[27]基于切机组织样本,预测了频率最低值及其对应时刻,提高了深度置信网络的预测精确度。文献[28]将各发电机的电磁功率、机械功率、最大出力限制、对动态频率的影响因子等在内的22维数据作为输入特征值,通过深度置信网络准确预测了受扰动后电力系统的频率曲线。文献[26,28]精准预测频率最低值,但是未比较其他频率关键特征值的准确性,结构复、参数众多,训练速度较慢。文献[29]利用卷积神经网络,提取了数据的空间相关性,在反映系统频率的时空分布特性基础上,准确预测了频率的关键特征值。文献[30]使用长短时记忆网络,预测的电力系统频率动态特征与仿真结果高度吻合,有效地解决了输入神经元在大规模互联电网中数量过多的问题。文献[31]使用v-支持向量(v-SVR)回归算法预测系统扰动后的频率特征,但由于v-SVR算法特性,用于预测系统动态频率曲线时,无法考虑频率的时序变化特征。文献[32]提出使用梯度提升决策树对电网频率模型进行预测,具有较高的准确率和计算速度,并对异常数据有较强的抗干扰能力。文献[33]将极限学习机(extreme learning machine, ELM)引入到系统频率安全裕度评估中,然而ELM算法结构简单、鲁棒性较差,当有较多量测装置传递到调度中心信息有误时,单层ELM能否有效提炼输入特征信息是一个问题。文献[34]在此基础上,使用多层ELM,通过深层结构建立输入与输出之间非线性映射关系,提高模型泛化能力。文献[35]基于深度神经网络和多层ELM,利用电力系统实时监测数据预测评估系统频率稳定性,取得了较好效果,但同样有参数及模型结构确定困难的问题。
为满足双高电力系统的实际需求,可将模型驱动与数据驱动结合起来[36],融合两种方法的优点,提升方法的整体性能,适用于解决复杂物理问题。文献[37 - 38]提出物理-数据融合方式,将SFR模型的结果结合系统信息共同输入到ELM中,得到系统频率响应结果,然而所使用的方法过于简单,物理-信息融合能力有待进一步考证。文献[39]利用频率响应模型进行初步频率预测,然后用深度神经网络对预测结果进行优化,然而其频率响应模型过于简化,频率预测结果不够精确。文献[40]在门控循环单元神经网络中嵌入频率响应相关物理知识,通过基本输入特征量和所嵌入物理知识形成新的输入特征量并用于模型训练,然而该文献的物理-信息建模方法为串联式,无法深入体现物理-信息模型各自的优势。综上,文献[37 - 40]物理-信息预测模型存在融合方法简单,建模方法较差等问题。因此,亟须研究新的基于物理-信息融合的频率预测方法,高效结合精准建模后的频率响应模型和人工智能预测模型。
上述4种方法之间是非替代的关系,应用于不同的场所和目的。
2 基于广域测量技术的频率时空分布模型
大电网动态频率变化存在延时和具有明显时空分布的特征[41 - 42]。在电力系统发生扰动时,频率的动态变化从扰动位置向四周传播,不同时刻和不同断面节点存在不同频率动态特征[43],由于惯量对不同节点、不同时刻的频率阻碍作用不同。如图8所示,绘制不同时间断面同一节点的惯性分布,得到系统的惯性分布图,清晰表示电力系统惯性时空特性。传统电网频率响应模型虽可较快反映频率的动态过程,但预测结果未能精细化反映频率的时空分布特性。因此,建立准确的频率时空分布模型,对于研究电网频率动态和制定控制策略具有重要意义。
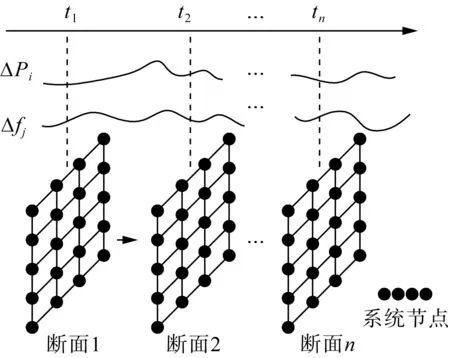
图8 电力系统频率时空特性示意图Fig.8 Schematic diagram of frequency temporal and spatial distribution model of electric power system
近年来广域测量系统WAMS发展迅速,其基本结构如图9所示。WAMS可为频率在线感知预测提供大量实时数据,记录扰动后系统频率动态的精确曲线。WAMS量测曲线可与数值仿真计算相结合,来研究电力系统频率特性[44],为建立频率时空分布模型提供支撑。
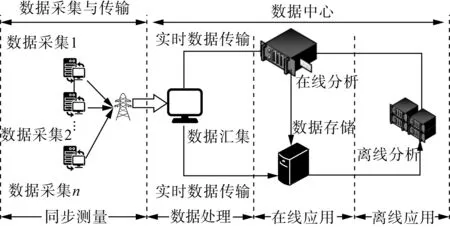
图9 广域频率态势感知的结构示意图Fig.9 Structure diagram of wide area frequency situational awareness
文献[45]基于WAMS技术,获得了电网实时频率数据,从物理解析和数值解析两方面提取了东北电网动态频率时空分布特征,分析了动态过程中对频率时空动态的影响因素。文献[46]提出的连续介质模型方法,结合WAMS各测点数据,可有效研究动态频率的时空分布特性。文献[47]引入了影响系统频率时空分布特征的关键参数,建立了广域电力系统时空分布模型,可研究电网惯性中心频率与WAMS各测点频率动态间的映射关系。文献[48]引入了基于滑动数据窗的机电波到达时间判断函数和判断准则,提出了基于WAMS实测频率数据的扰动在线定位技术。文献[49]基于频率波方程和频率波色散关系,提出频率动态时空分布特性的新方法。文献[45 - 49]基于连续体模型的频率传播及分布理论研究互联电网的频率时空分布特性,难以应用于实际大型互联电网。频率安全评估借助 WAMS系统进行估计双高电力系统的惯量水平,可以用系统非同步发电渗透率(system non-synchronous penetration, SNSP)来刻画[50]。电力系统的频率响应特性与 SNSP 密切相关,体现了节点惯量对于电力系统频率动态机理的深刻影响。
文献[51]提出了在类噪声信号下,通过阶跃响应下的系统各节点惯性系数提取方法,得到大系统各节点的惯量分布情况,进而得到时空特性分布图,但该评估方法对节点惯量测量方法的速度和精度还有待提高。文献[52]首先基于转子运动方程得到系统的总惯量,然后通过提高曲线拟合自适应性的可变阶多项式频率-功率拟合方法,来完成惯量的提取。这种方法显著提高了测量的精度,但较为复杂。文献[53 - 54]提出了一种在线算法来估计系统扰动发生的时间及系统在扰动后的惯量,该方法需要连续在线处理有功功率和频率变化率的滑动窗数据,估计结果受滑动窗数据长度的影响。文献[55]提出了一种基于拓展卡尔曼滤波器的同步机惯量常数估计方法,但该方法必须在系统扰动发生的瞬间及时启动,否则会在惯量常数估计过程中引入较大误差。文献[56]从过滤扰动前后有功功率噪声角度出发,研究多个滑动数据窗口的节点惯量评估方法,可以动态提取系统的惯量。惯量评估算法一方面配置量测装置,准确、快速地提取惯量评估所需的节点功率和频率类噪声信息,另一方面,将惯量时空分布评估结果转化为预警信息和可视化图像,指导调度部门进行快速、有效的决策。
3 基于频率模型的新能源控制和低频减载优化
第2节对电网频率响应模型的建模方法进行了综述。本节重点针对考虑不同控制策略的复杂系统频率模型进行论述,主要包括新能源电站新型调频控制和电网低频减载策略。
3.1 基于频率模型的新能源控制优化
作为新型电源,新能源机组不同运行工况会对“双高”电力系统频率动态产生重要影响,新能源发电机组参与调频的频率稳定至关重要[57 - 59]。文献[60 - 63]考虑了不同类型的风电机组频率建模,得到了系统频率动态响应特性和风机转速之间的关系。文献[64 - 65]建立了加入新能源一次调频后的线性化数学模型,并引入了常规同步机组发电系数,建立了新能源高渗透率的电力系统简化聚合频率模型。文献[66]考虑了电力系统整体风电出力的不确定性,引入了风力发电机一次频率响应的概率算法来改善系统频率模型的精度和适用性,但文献[60 - 66]均未评估其模型在实际电网中的适用性。
新能源虚拟惯量控制对系统频率动态特性的影响,目前正成为研究热点之一。如风机、光伏虚拟惯性响应、虚拟一次频率响应、与储能联合频率响应、自适应调节的虚拟惯量频率控制等控制策略[67 - 69]。所以新能源机组的SFR模型可分为两个部分,一部分是参与调频的常规机组的精准频率响应模型,另一部分是采用虚拟惯量控制、一次调频等由控制引入的惯量环节。首先建立包含不同原动机调节特性、原动机限幅环节、同步机调差死区环节等实际约束环节的调频同步机组精细化频率模型,其次附加综合新能源惯量模拟控制和一次频率控制环节,如图10所示[70],其中ΔPrj为新能源电站频率响应功率,Hrj和Drj分别是模拟惯性时间常数和一次调频下垂系数。文献[71 - 72]建立了采用虚拟惯量控制并网换流器的系统SFR模型,但并未明确新能源电源发电边界。文献[73]提出了区分一次调频和惯量响应的有效调差系数和有效惯量比例系数,得到了新能源高渗透率电力系统的聚合频率响应模型,提高了频率模型在高比例新能源、多直流馈入系统的适用性。
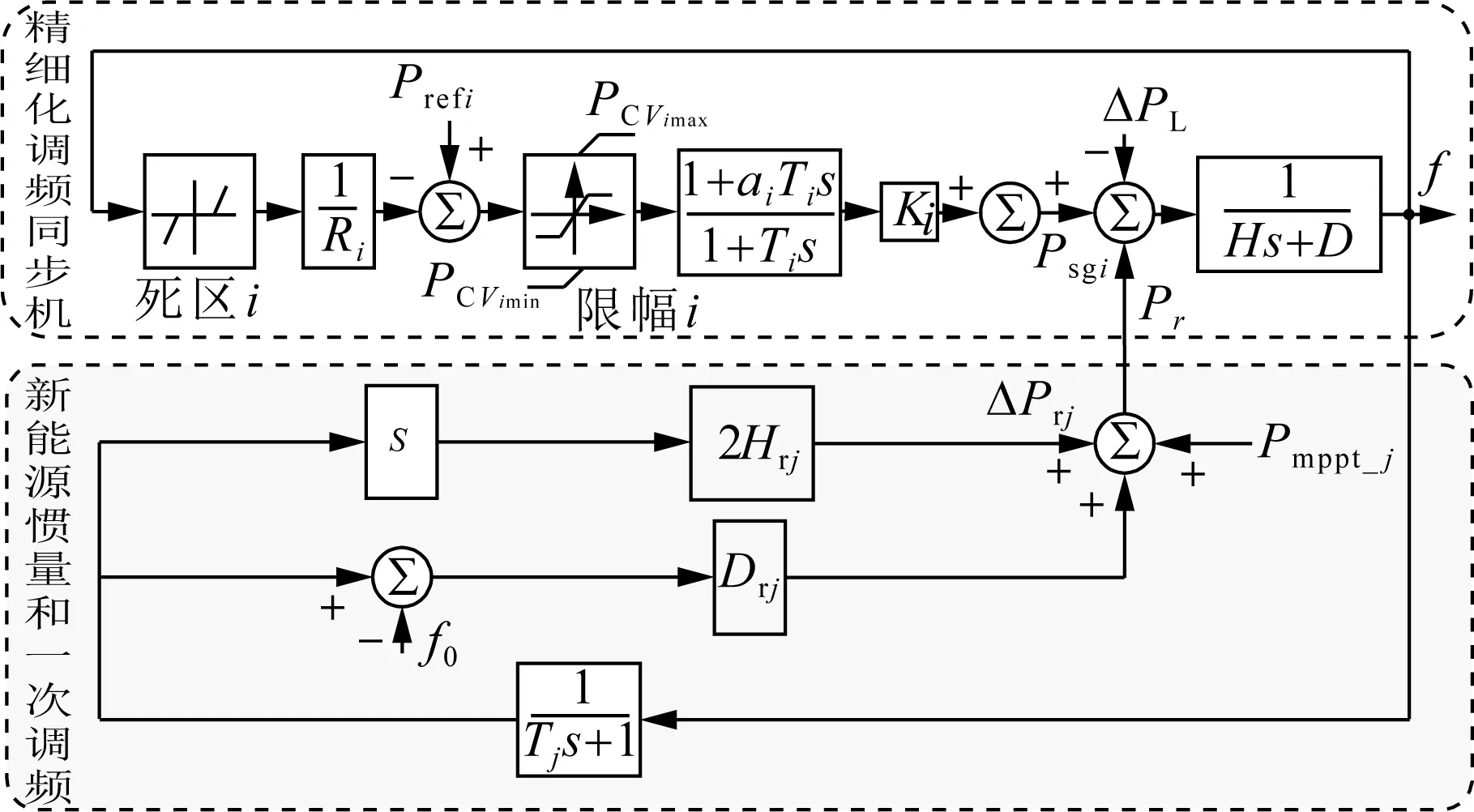
图10 考虑风机转子SFR模型示意图Fig.10 Schematic diagram of SFR model considering wind rotor
3.2 基于频率模型的低频减载策略优化
当系统发生严重故障,作为系统第三道防线,低频减载策略可分级切除指定负荷,可有效避免频率失稳现象,通过频率模型进行低频减载的优化意义重大。文献[74 - 75]基于时域仿真频率模型分析了电网频率响应特性,提出了通用性较强的低频减载整定方案,校核已有的低频减载整定方案。文献[76]研究分析了大电网频率动态响应过程和影响因素,为低频减载阈值的设置提供了参考。文献[77]建立了电网频率响应时域模型,基于频率实测轨迹对低频减载整定进行了分析和优化。文献[76 - 77]整定优化低频减载方案,但是未能做到精准减载,容易造成负荷过切。
文献[78]建立了考虑低频减载的频率响应模型,如图11所示,利用该模型可求解频率响应的具体解析解,进而评估低频减载对频率影响的效果,但是并未考虑负荷的分布特性及影响程度。文献[79]在经典频率响应模型的基础上,提出了定义低频减载节点的综合指标,进而确定了负荷减载量及减载位置。文献[80]建立了多目标优化低频减载模型,该模型可以有效避免负荷过切,提升系统稳定性。文献[81]提出了考虑系统频率初始变化率ROCOF的低频减载策略,提高了电网对频率紧急控制的速度和能力。
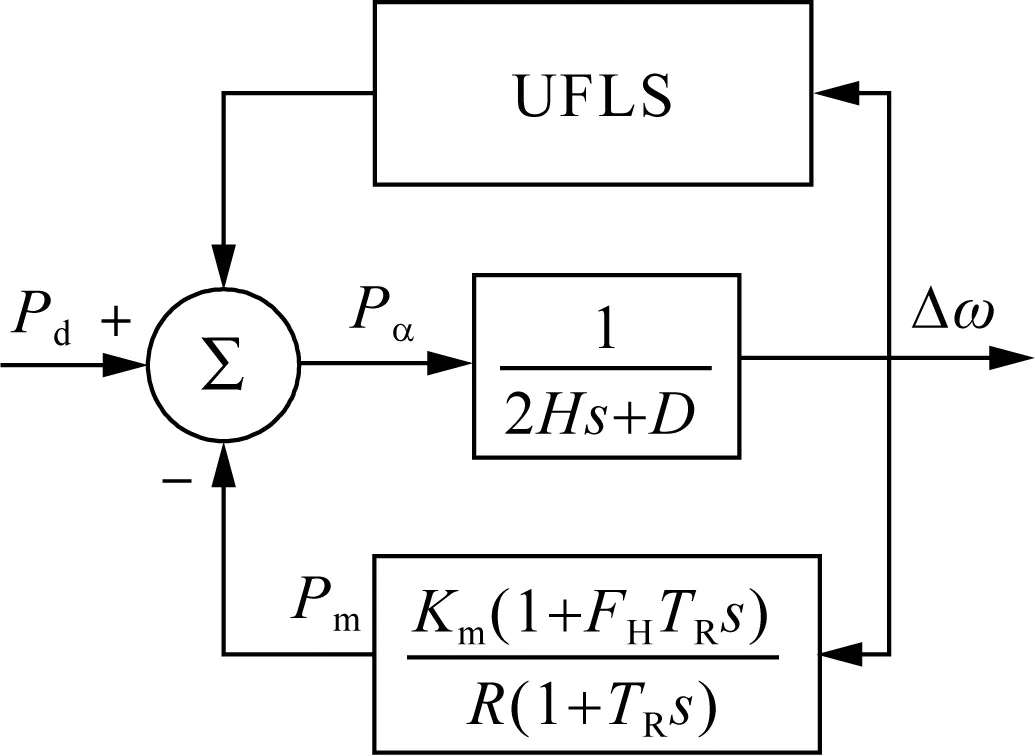
图11 考虑低频减载的SFR模型示意图Fig.11 Schematic diagram of SFR model considering low-frequency load shedding
4 展望
随着新能源在未来电网中的比例不断提高,电网频率稳定运行面临更加严峻的挑战,优化频率响应模型、分析频率时空分布特性、改进新能源调频控制和低频减载等研究变得愈加重要,建立考虑未来电力系统新特性的精确全网频率模型成为电力系统调度不可或缺的分析工具。以下4点是未来亟须解决的关键问题。
随着电力系统短路比的下降、传统直流输电的不断接入、配电网输电线路逐步阻感性以及有功无功耦合负载的不断增加,电力系统的有功功率和无功功率耦合趋势越来越明显。已有的频率响应模型构建方法,目前主要集中在有功功率对新能源输出频率的控制。然而,无功功率会影响并网侧电压,间接影响了有功功率的控制,一定程度上会对输出频率产生影响。已有研究忽略了无功功率-电压动态对电网频率特性的间接影响。因此,需从建模和分析方法上考虑电网无功功率-电压动态对频率影响的规律,改善传统频率模型的精度。
大型复杂电网的频率响应时空分布特征显著,已有研究大多针对单个区域内母线各处的动态频率时空分布特性,未充分考虑多区域间的频率分布和交互影响。需基于WAMS技术进一步考虑广域电网多区域间的频率时空分布特性。
基于电网频率模型生成历史数据,利用深度学习进行训练的频率预测方法,预测精度和泛化能力取决于数据样本的多样性。为使训练后的深度学习模型适用于各种可能场景,深度学习方法可与迁移学习等方法进行结合,建立自适应频率响应模型,提高人工智能方法与频率预测模型的实用性。
具有快速一次调频、虚拟惯量模拟等新型控制的新能源发电并网比例增加。锁相环、虚拟惯量控制、MPPT控制等控制环节的引入增加了新能源频率预测的复杂性。因此,有必要研究这些新型控制对新能源输出频率的影响机理。调频电源多元化和调频方式多样化将使频率动态响应机理的复杂程度显著提高,亟须一种涵盖传统发电机组、新能源新型调频控制、网荷动态响应等更加精细化的综合频率响应模型,以准确刻画不同类型新能源电源对系统频率响应的贡献,从而进一步充分、合理挖掘各类新能源的调频作用,提高大电网在线有功频率的态势预测准确度。
5 结语
随着新型电力系统的不断发展和国家“双碳”目标的进一步落实,大量新能源将接入电网,改变系统的频率特性,使电网运行和调度面临更为严峻的挑战。本文从频率模型构建和分析方法、基于广域量测技术的频率时空分布模型、基于频率模型的新能源控制和低频减载优化3个方面进行了详细综述,最后展望了频率模型构建方面亟须进一步研究的热点问题,为相关研究提供了参考和建议。

