基于KPCA-ISSA-KELM的光伏阵列故障诊断方法

武文栋，施保华，郑传良，郭茜婷，陈 峥

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.国网福建宁德供电公司，福建宁德 352100；3.湖北省微电网工程技术研究中心，湖北宜昌 443002）

0 引言

在“双碳战略”的目标下，寻找和利用新型清洁的可再生能源已成为当今世界的主要研究热点[1-3]。近年来，我国光伏发电技术的进步和光伏并网发电规模的不断扩大，在恶劣的自然环境下工作的光伏阵列面积大、分布广，容易出现组件短路、开路、老化和局部遮阴等故障[4-7]。这些问题对光伏电站整体的运行和发电效率产生了较大影响，因此高效准确地对光伏阵列故障进行诊断具有重要的意义。

近年来，针对光伏阵列的故障诊断方法已有许多专家学者展开了相关研究工作。基于研究对象不同，故障诊断技术可大致分为：传统检测法、数学模型分析法和智能算法检测法等[8-11]。文献[12]利用光伏阵列在正常和故障时组件温度不同，采用红外图像识别各种故障，但该方法成本较高，无法大规模应用。文献[13]提出一种预测模型的故障诊断方法，该方法利用实验值与预测值的差值来区分故障种类，受模型训练参数影响较大，故障动态诊断性能不高。近年来，人工智能算法被应用于光伏阵列故障诊断技术中，文献[14]提出一种基于高斯核模糊C均值聚类的光伏阵列故障诊断方法，通过增加一个新的特征量对不同故障进行表征并聚类获取类心，并训练获得相似度，从而实现故障分类。文献[15]提出一种基于自适应权重粒子群对反向传播（Back Propagation，BP）神经网络优化的光伏阵列故障诊断方法，利用BP 神经网络诊断模型分析其输入和输出，训练过程简单高效，对故障诊断具有较强的实时性。文献[16]提出核极限学习机（Kernel Extreme Learning Machine，KELM）方法，利用基于Eagle 策略的混合自适应Nelder-Mead 单纯形算法（Eagle Strategy Based Hybrid Adaptive Nelder-Mead Simplex Algorithm，EHA-NMS）参数识别对核极限学习机模型的输入参数进行寻优，有效改善了模型的鲁棒性和稳定性，对光伏阵列故障识别有较高的诊断精度。

为了进一步提高模型的识别准确率、稳定性和泛化能力，提出了一种基于KPCA-ISSA-KELM 的光伏阵列故障诊断方法，通过核主成分分析法（Kernel Principal Component Analysis，KPCA）[17-18]分析并提取故障数据的非线性特征，再对故障样本数据输入KELM 进行训练，同时利用改进后的麻雀搜索算法对KELM 的核参数和正则化系数进行优化，提高KELM 分类准确率，最后利用该模型对光伏阵列的各种故障进行诊断。通过实验平台采集的实验数据验证了该模型的有效性，试验结果表明KPCAISSA-KELM 能够对光伏阵列出现的复杂故障进行有效诊断，故障诊断准确率达到97%，优于其他诊断模型。

1 算法原理

1.1 核主成分分析

核主成分分析[19-20]的特点是基于核函数将原故障样本数据变换至高维空间F，然后在线性子空间中通过降维获得低维数据特征，从而提取出光伏阵列诊断模型输入的样本特征主成分。避免了复杂故障出现时数据特征相似而导致的诊断精度下降问题。

1）KPCA 将原始故障样本数据映射到高维空间φ，形成新的数据φ（ei）={φ（e1），φ（e2），…，φ（en）}，i=1，2，…，n。假设在高维空间中样本已中心化，则协方差矩阵为：

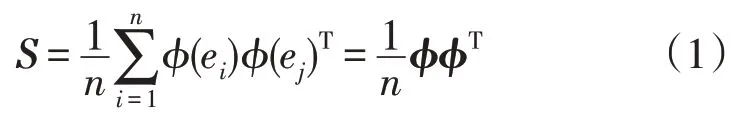
2）引入核函数为K*=φTφ，对S中数据进行主成分分析求解：

式中：λ为特征值；η为特征向量。

3）设置累计贡献率为85%，降序排列取前s个特征值λj（j=1，2，···，s）和其对应的特征向量ηj（j=1，2，…，s）：

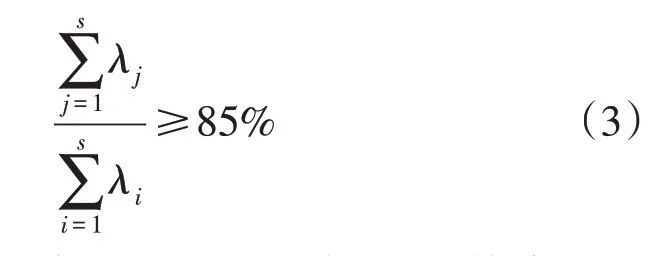
4）当累计贡献率达到设定要求时，计算降维映射后的非线性样本G：

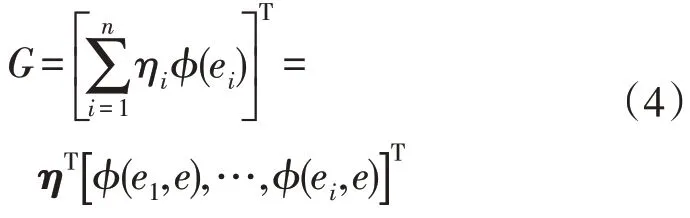
1.2 麻雀搜索算法原理与改进

根据自然界中麻雀群体觅食和反捕行为，薛等人于2020 年提出了麻雀搜索算法[21]（Sparrow Search Algorithm，SSA），麻雀群体觅食过程中有一个明确的劳动分工：发现者、追随者和预警者。

发现者作为种群的觅食向导，需要不断搜索广阔的区域并更新位置。因此在麻雀种群迭代计算时，发现者的位置更新公式为：

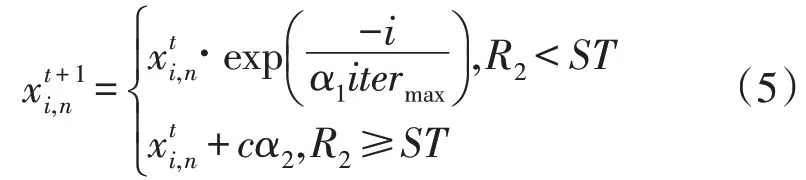
式中：为种群中的第n个元素值；为麻雀i在第t次迭代的当前位置；itermax为种群可迭代极值数；α1和α2为（0，1）之间的均匀随机数；R2（R2∈[0，1]，单只麻雀个体的随机值）和ST（ST∈[0.5，1]）分别为危险性和安全性的范围阈值；c为服从正态分布的随机数。

追随者的位置更新公式为：

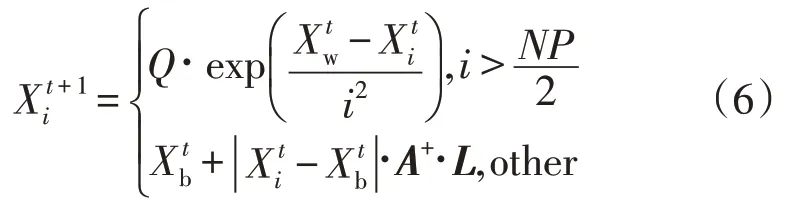
式中：和分别为发现者搜索当前全局的最优位置和最劣位置；Q为符合正态分布的任意值；A为元素为随机数1 或-1 的1×d矩阵；L为元素均为1 的1×d矩阵；NP是麻雀种群数量。

预警者的位置更新公式为：

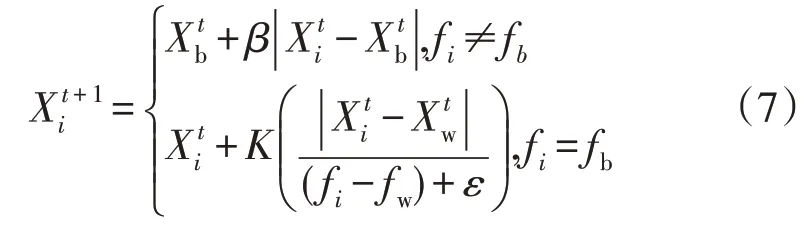
式中：β为符合正态分布性质的步长控制参数；K∈[-1，1]为一个随机数值；fi，fb和fw分别为当前第i只麻雀的适应度值、当前全局最优适应度值和最劣适应度值；ε为无限接近但不等于0 的常数。

在解决工程实际问题中，麻雀个体收敛速度过快容易收敛到局部极值点使算法进入“早熟”，导致收敛精度不高。此外，算法迭代末期由于麻雀个体仅在区域内的较短范围进行局部搜索，使算法收敛速度降低，难以获取全局最优解。

对麻雀搜索算法进行改进，采用以下2 个策略提升麻雀搜索算法的全局寻优能力。

1）针对算法初期，通过融合Levy 飞行策略[22]对麻雀种群初始化，使得发现者位置更加随机多样，部分麻雀个体可以在区域内较大范围进行全局搜索，扩大了发现者搜索区域，提高种群总体的寻优效率，因此更新后的发现者公式为：

式中：δ为一个步长参数；Levy（s）服从莱维分布，其飞行步长公式为：

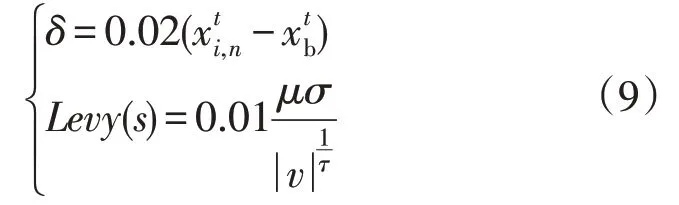
式中：μ和v均为[0，1]间的标准正态分布随机数，常数；τ=1.5；σ为一个关于Γ和τ的常函数。

2）针对算法末期可能出现停滞现象，引入自适应权重t，增强麻雀种群全局收敛能力，使得麻雀在当前最优位置附近范围进行随即搜索，若发现更优位置则更新，否则位置保持不变，从而提高麻雀种群跳出局部极值点束缚的概率。

更新后的追随者公式为：

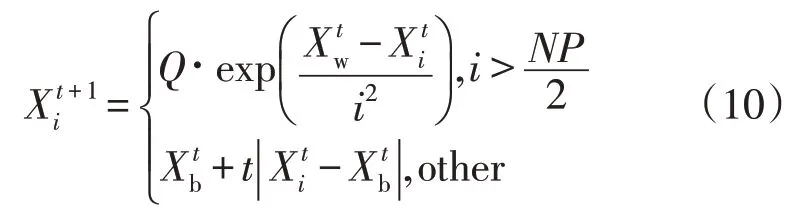
其中自适应权重φ的调整公式为：

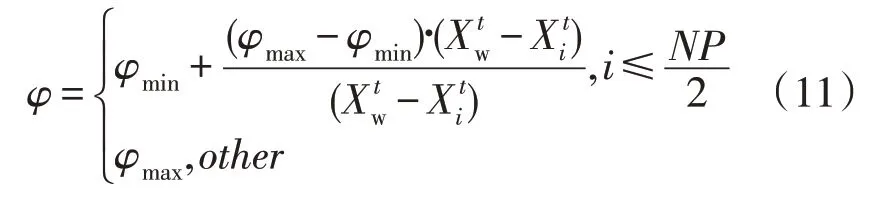
式中：φmin和φmax分别为自适应权重的最小值和最大值。

1.3 算法验证

为了验证改进麻雀搜索算法（Improved Sparrow Search Algorithm，ISSA）的寻优性能，采用两种测试函数进行迭代测试，并与SSA 算法和粒子群优化（Particle Swarm Optimization，PSO）算法进行对比，取最大迭代次数为1 000，种群规模r=50。ISSA，SSA 和PSO 算法对测试函数的寻优收敛曲线如图1 所示。

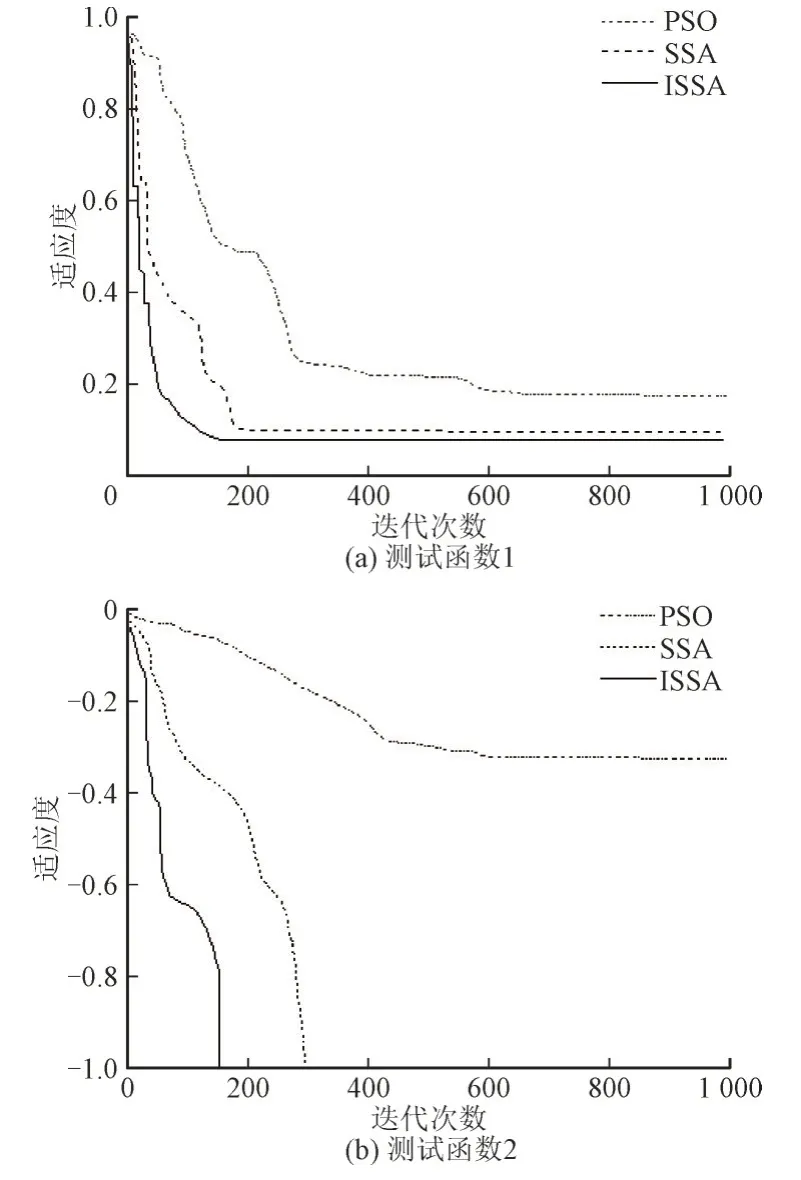
图1 算法寻优结果Fig.1 Optimization results of algorithms

测试函数1 选择为最优解远离原点，从图1（a）中得出，ISSA 算法在迭代初期收敛曲线变化更为陡峭，迭代160 次左右达到稳定，同时适应度达到0.076 左右，很好的满足了精度要求；SSA 算法在迭代接近200 次趋于稳定，且适应度为0.094；PSO 算法迭代600 次左右才能趋于稳定，适应度仅为0.172，收敛精度较差。

测试函数2 选择为最优解收敛于原点。从图1（b）中可以看出，ISSA 与SSA 算法均可以收敛到理论最优值，且ISSA 算法寻优精度更高，收敛速度更快，而PSO 算法陷入了局部最优。ISSA 算法迭代到达稳定所用时间为1.066 s，SSA 算法为1.731 s，PSO算法则用了3.863 s。因此改进后的麻雀搜索算法在迭代次数、收敛时间和收敛精度上均优于其他算法。

2 光伏阵列故障诊断模型研究

2.1 故障特征参数的选取

通过对光伏阵列多种故障状态下I-U曲线和P-U曲线的特性分析发现[23-27]：不论发生哪类故障，均会导致光伏阵列的最大功率点电压值Umpp、最大功率点电流Impp、开路电压Uoc、短路电流Isc发生明显变化，因此光伏故障诊断模型的特征参数选择Umpp，Impp，Uoc，Isc作为输入层变量。

2.2 故障诊断模型输出层定义

以10×4 的实际光伏阵列为故障分析对象，工作状态可分为5 类，分别为正常、短路、局部阴影、老化、开路。但在实际工况中光伏阵列可能出现多故障的情况，因此根据可能出现故障类型，设计出8 种故障情况，故障诊断模型的输出层定义如表1 所示。

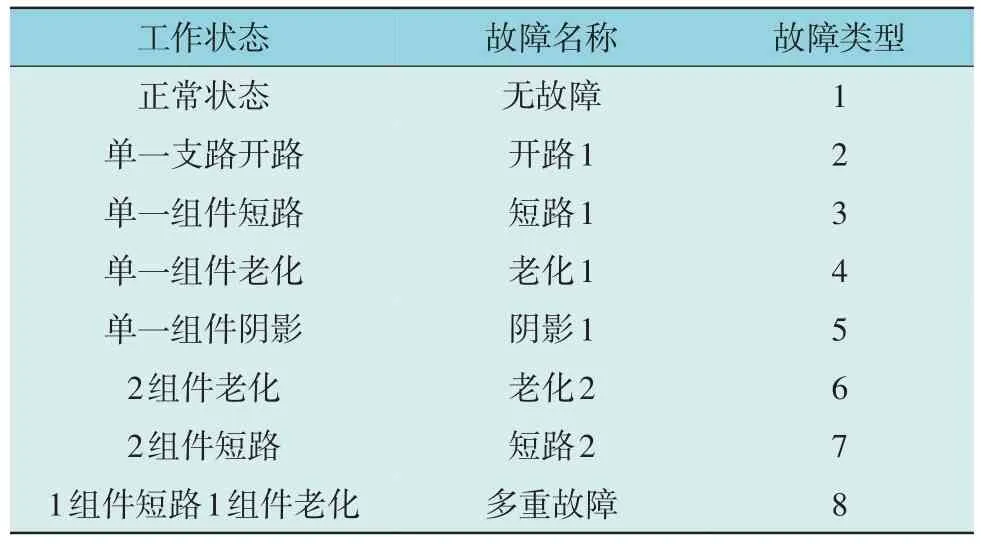
表1 故障诊断模型的输出层定义Table 1 Output layer definition of fault diagnosis model

2.3 核极限学习机

极限学习机[28]（Extreme Learning Machine，ELM）中隐含层的权重是随机赋值或人工给定的。在训练时只需计算输出层权值，简化了网络参数设置，学习速度快。

在ELM 算法中：

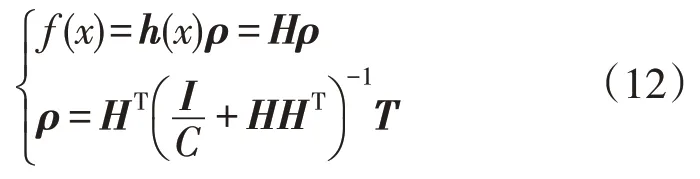
式中：x为给定的训练样本输入；f（x）为网络实际输出；h(x)为样本矩阵；H为网络隐含层输出矩阵；ρ为隐含层与输出层连接权重向量；T为训练样本类别向量矩阵；I为对角矩阵；C为正则化系数。

ELM 通过随机赋值生成的隐含层输出矩阵H，随机映射导致建模时会生成不同的输出矩阵H，进而导致输出层权重向量ρ不同，使得ELM 模型输出的稳定性和鲁棒性较差。为提高ELM 的泛化性能和稳定性，Huang 等采用核函数对ELM 进行优化，改变ELM 中隐含层的特征映射，形成了基于核的ELM 算法，KELM 不仅保留了ELM 的优点，而且增强了泛化能力，具有更强的鲁棒性，优于ELM 与支持向量机（Support Vector Machine，SVM）的拟合能力和计算效率，进一步提高了分类精度。

定义KELM 核矩阵ΩELM代替HHT，其公式如下：

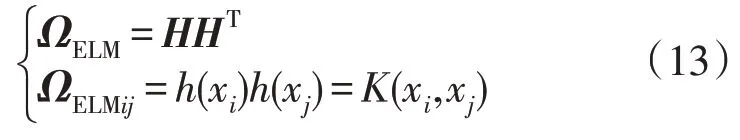
式中：xi和xj为输入样本。

K（xi，xj）选择为RBF 核函数：

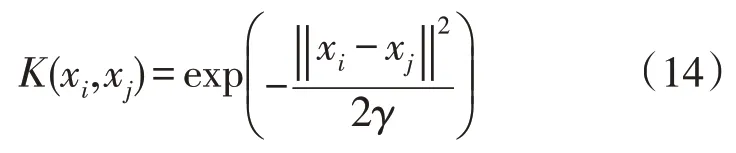
式中：γ为核参数。

因此KELM 模型的输出为：

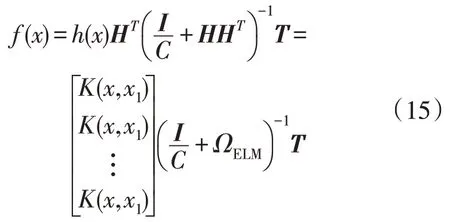
其中，KELM 模型中的核参数γ和正则化系数C会影响模型的性能，文中采用ISSA 算法对其进行优化。

2.4 基于KPCA-ISSA-KELM的故障诊断模型

针对8 种光伏阵列常见故障进行诊断。由于实际环境采集的故障诊断数据分布复杂而导致的故障诊断准确度下降，基于KPCA 将故障样本数据映射到高维空间，消除空间相关性与因辐照度温度等对不同故障特征产生的冗余数据，进而提取数据的非线性特征主元，并将采集数据分为训练数据集和测试数据集。利用融合Levy 飞行策略和自适应权重t对SSA 算法进行改进，增强了其寻优效率，并采用ISSA 对KELM 进行参数优化，建立基于KPCA-ISSA-KELM 的光伏阵列故障诊断模型，流程如图2 所示。

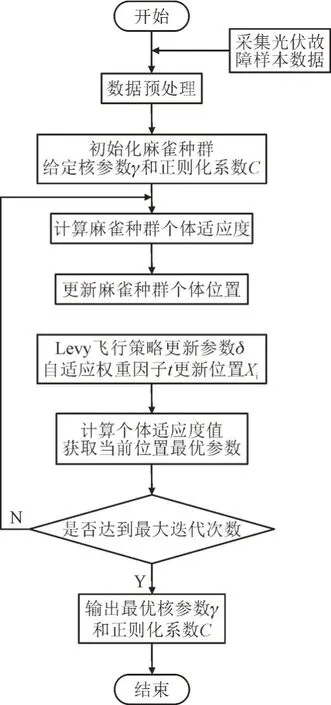
图2 基于KPCA-ISSA-KELM的故障诊断算法流程图Fig.2 Flow chart of fault diagnosis algorithm based on KPCA-ISSA-KELM

3 实验分析

3.1 光伏阵列故障数据采集

图3 为福建省电力公司风光储微网项目-海上光储实验平台。在实际工作环境下设定故障时的光伏阵列光照强度为200～1 000 W/m2的区间内，各个阵列模块的环境温度则设置为25 ℃～45 ℃内，利用10×4 的光伏阵列电池组进行8 种故障实验，并采集故障数据样本。其中光伏阵列电池组如图4 所示，电池及阵列的具体规格参数如表2 所示。表2 中Umpp为最大功率点电压，Impp为最大功率点电流，Uoc为开路电压，Isc为短路电流。

图3 海上光储实验平台Fig.3 Experimental platform for offshore PV energy storage

图4 10×4的光伏阵列电池组Fig.4 10×4 PV array battery pack

表2 光伏阵列电池组的规格参数Table 2 Parameters of PV battery strings

实验在放晴、多云和阴雨等不同气候环境下完成数据的采集工作。分别设置8 种故障情况，按故障类型分别收集数据，每种故障采集300 个数据样本，共计2 400 组。同时取出70%数据作为故障诊断模型的训练样本，其余30%作为模型的测试样本。

3.2 实验参数设置

实验所用计算机配置为Win10 64bit 操作系统，Intel（R）Core（TM）i5-11400H CPU 4.50 GHz 处理器，16GB DDR4 运行内存，编程软件为MATLAB 2020a。设定各算法的最大迭代次数为100，种群规模为30，其中PSO 惯性权重为0.9 和0.2，加速度系数为2；ISSA 和SSA 的安全阈值设为0.6。

3.3 实验结果分析

为验证文中模型的有效性，将720 组测试样本数据分别输入KPCA-ISSA-KELM，KPCA-KELM，ISSA-KELM 和KELM 诊断模型中进行诊断。4 种模型的故障诊断结果如图5 至图8 所示。

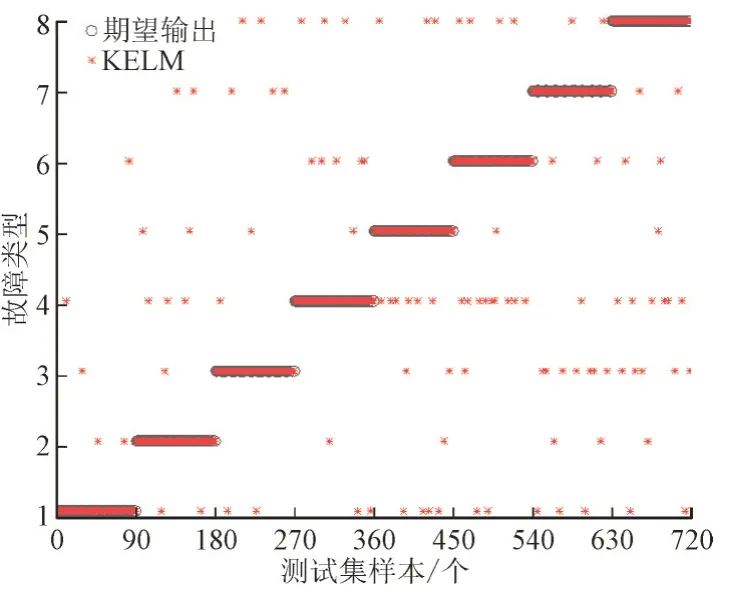
图5 KELM故障诊断模型的结果Fig.5 KELM fault diagnosis model results

由图5 可知，KELM 故障诊断模型的诊断精度最低，对光伏阵列所出现的8 种故障类型诊断效果均不理想，极易被误诊成其他故障类别。

由图6 可以看出，ISSA-KELM 故障诊断模型中，通过改进的麻雀搜索算法优化核极限学习机的核参数γ和正则化系数C后，各类故障的诊断精度都有所提高，但是对于多故障情况诊断结果仍较差。

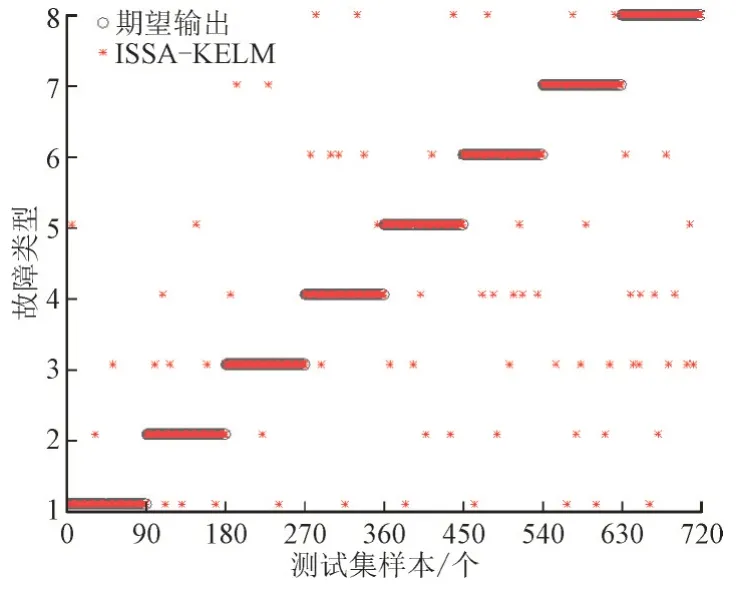
图6 基于ISSA-KELM故障诊断模型的结果Fig.6 Result diagram of fault diagnosis model based on KPCA-KELM

由图7 可得，KPCA-KELM 故障诊断模型对光伏阵列多故障诊断效果较好，且单一故障不会被误诊为多故障的情况，说明KPCA 可以更好的挖掘数据特征，可以高效区分单一故障和多故障，提高了多故障诊断精度。

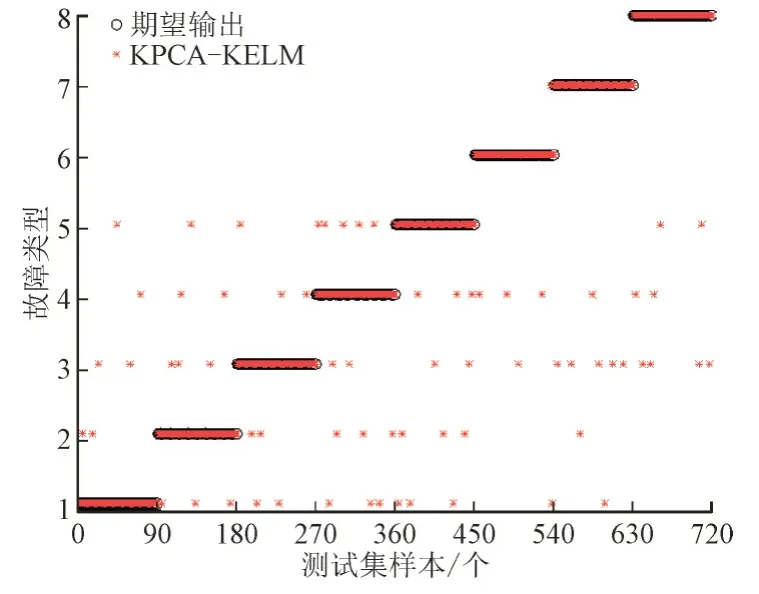
图7 基于KPCA-KELM故障诊断模型的结果Fig.7 Result diagram of fault diagnosis model based on KPCA-KELM

由图8 所示，在本文提出的KPCA-ISSA-KELM诊断模型中，将KPCA 提取的特征主成分输入经过ISSA 优化后的KELM 模型，可以对光伏阵列所出现的各类故障进行高效率诊断，且由于对故障数据进行了核主成分分析，对原始故障数据提取特征主成分，有效区分了单一故障和多故障情况，使得在多故障情况下误诊数减少，同时采用改进麻雀搜索算法对KELM 的γ和C进行优化，提高了开路、短路、组件老化和局部阴影故障类型的诊断精度。该模型的整体故障诊断效率均高于其他故障诊断模型。

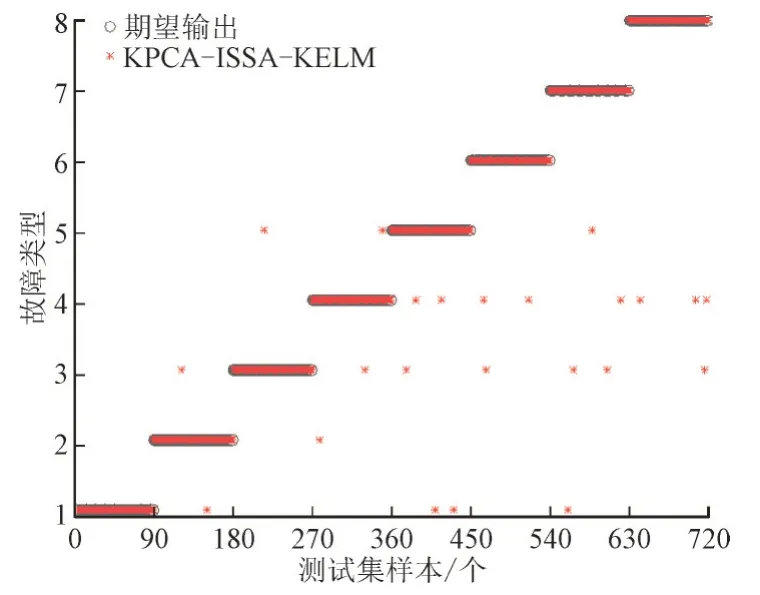
图8 基于KPCA-ISSA-KELM故障诊断模型的结果Fig.8 Result diagram of fault diagnosis model based on KPCA-ISSA-KELM

文中所提4 种故障诊断模型的故障诊断结果对比如表3 所示。KPCA-KELM，ISSA-KELM，KELM 和本文方法的平均精度分别为90.7%，90.3%，85.6%和97%。针对同样的故障数据，传统KELM 模型的故障诊断精度低于90%，其他3 种模型均能达到90%以上。KPCA-KELM 与KPCAISSA-KELM 模型之所以能够达到较高的诊断精度是因为核主成分分析可以将光伏阵列的故障样本信息映射到高维空间，除去冗余数据并提取出了非线性数据主元，极大降低了单一故障与多故障间的误诊情况。同时，对于光伏阵列发生的开路和短路2 种故障状态的诊断精度都明显高于局部阴影和组件老化这2 种故障。前者是因为这2 种故障类型均有明显特征，易于诊断。后者是由于受多种因素影响，局部阴影和老化故障在低温和弱光照的条件下，使得故障模型无法较高精度地将其与正常状态区分出来，所以更易出现误诊断，诊断难度较大。

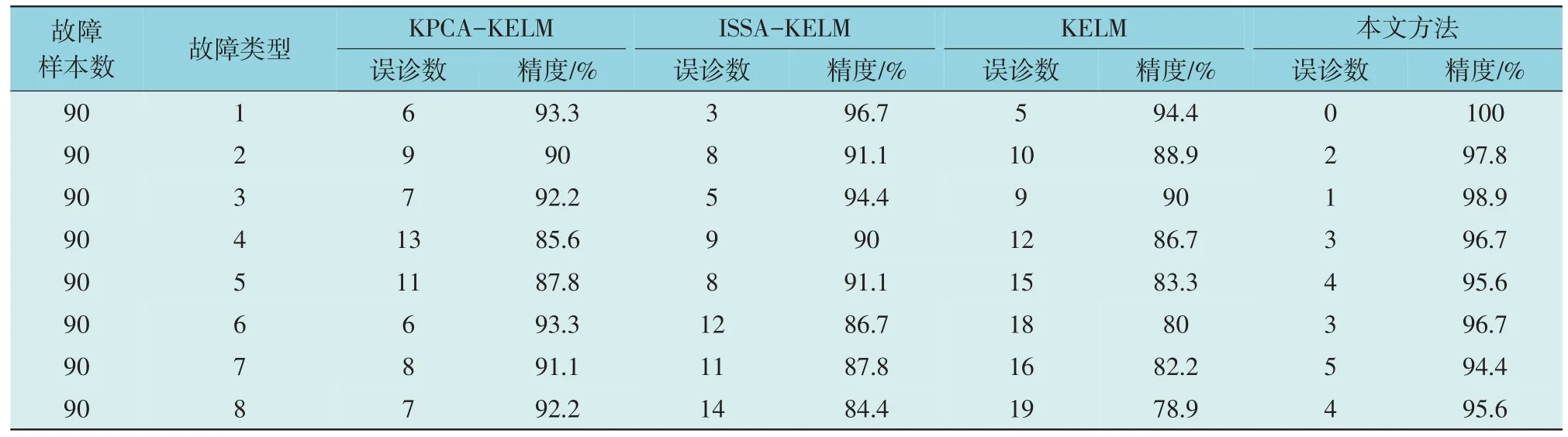
表3 不同模型的诊断精度Table 3 Diagnostic accuracy of different models

综上，文中所提的基于KPCA-ISSA-KELM 故障诊断模型不仅可以对光伏阵列的单一故障有较好的诊断精度，而且对多故障情况也可以准确识别，整体的故障诊断精度更高。

3.4 故障诊断模型评价

为了验证文中所提诊断方法实验结果的稳定性和泛化能力，文中选取均方误差（Mean Squared Error，MSE）、平均绝对误差（Mean Absdute Error，MAE）和决定系数（R2）作为评价指标对4 种模型的预测诊断效果进行评价，MSE 的值用EMS表示，MAE的值用EMA表示，具体公式为：

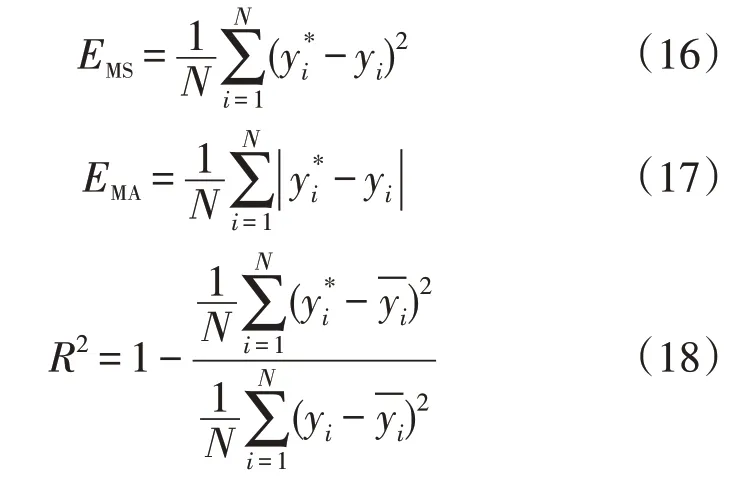
式中：N为测试样本数目；yi为实际值；为模型预测值；为实际值的平均值。

表4 为各个预测模型的仿真评价指标。从表4可知，EMS较KPCA-KELM 模型降低0.007 62%，EMA和较ISSA-KELM 模型降低1.15%，R2为4 种方法中最大，即模型拟合效果最好。

表4 各个预测模型的仿真评价指标Table 4 Simulation evaluation index of each prediction model

这是因为与KPCA-KELM 方法相比，本文方法具有较强的全局搜索能力，更好跳出局部极值；与ISSA-KELM 相比，本文方法降低了算法复杂度，更易于对复杂故障进行诊断。因此，分析综合指标可得，在确定故障诊断模型的输入变量和网络参数时，本文方法有更好的准确性和泛化能力，可以有效降低由非线性系统自身引起的偏离。

4 结论

针对光伏阵列故障难以被准确高效地诊断和分类问题，提出一种基于KPCA-ISSA-KELM 的光伏阵列故障诊断方法。该方法首先利用KPCA 突出故障样本数据特征差异，将单故障与多故障区分开，进而通过融入Levy 飞行和自适应权重t的SSA算法对KELM 的核参数γ和正则化系数C进行优化，获得光伏阵列最优故障诊断模型。实验验证了文中所提KPCA-ISSA-KELM 模型可以高效准确地诊断出光伏阵列的不同故障类型，诊断精度达到97%，对比传统KELM（85.6%）、KPCA-KELM（90.7%）和ISSA-KELM（90.3%），具有更高的故障诊断准确率。但在光伏阵列多重故障时的短路和组件老化等故障类别的诊断精度上还有待提高，下一步会深入研究光伏阵列多重故障诊断方法，提高诊断精度。