智能电网连续型社会福利最大化实时定价方法

罗艺灵，高 岩

（上海理工大学管理学院，上海 200093）

0 引言

随着产业结构的调整和人民生活水平的提高，我国电力消费增速加快，用电量的变化曲线波动越来越剧烈。电力系统的稳定运行要求供需实时平衡，然而仅仅依靠供给侧的调节很难实现这一平衡，因此，需要配合有效的需求侧管理[1-2]。实时定价作为需求侧管理最直接、有效的方法，是指通过电价信号激励电力用户自愿在谷期用电，从而削减峰期的负荷，达到削峰填谷的目标[2-3]。智能电表的应用有效实现了电力供给侧和需求侧双方的电力信息交互，为实时定价策略提供保障。电力系统研究中目标优化是比较常见的方法[4-5]。智能电网的实时定价策略研究常见的研究思路有2 种：一种是运用动态博弈理论[6-7]和双层优化方法[8-9]，另一种是基于社会福利最大化理论和影子价格理论[10]，运用对偶优化方法[2-3]。现有的研究中后者的运用更加广泛。

基于社会福利最大化的定价机制主要从公共产品的角度出发，被广泛运用到电力定价中。在智能电网实时定价策略的研究中，社会福利最大化模型同时兼顾了供需双方的利益。文献[10]最先将社会福利最大化模型运用到智能电网实时定价中，以实现用户的效用最大化和供电商的成本最小化为目标，以用户的效用减去供电商的成本作为目标函数建立智能电网实时定价的社会福利最大化模型，根据供电与用电的平衡为约束条件，运用对偶优化方法求得供、用电量和实时电价。许多学者基于文献[10]进行了一系列研究。社会福利最大化方法最初运用于研究一个供电商和多个用户构成的最基本的智能电网模型，随着研究的深入，学者们对社会福利最大化模型进行了不同角度的改进。首先是在基本社会福利最大化模型的基础上考虑用户侧的电器分类[9，11-12]，根据电器运行的特点一般分成必须运行的电器、弹性电器和半弹性电器3 类。随着太阳能、风能等可再生能源的发展，一些研究亦将可再生能源发电并入到了智能电网的实时定价研究中[13-15]，有的还考虑了储能装置[16]、双碳目标[9，17]、分类用户[18]、效用函数的形式[19]等。但是，文献[10-19]的实时定价研究都是基于离散的社会福利最大化方法，没有重点体现发电和用电的时间连续性这一重要特征对实时定价的影响。文献[20]首次提出了基于连续时间商品模型的电力市场实时定价，与以往研究的不同之处在于文献[20]提出的定价方式下的市场优化模型是连续的，优化问题也由传统的数值优化问题转变为泛函极值优化问题。

文献[20]主要考虑了电力系统中发电和用电的时间连续性，以电能平衡为约束条件，运用社会福利最大化理论对电力市场进行实时定价研究。但在实时定价原理的阐述方面，只考虑了发电侧的单边竞价成本最小，没有体现需求侧管理，也没有综合考虑用户侧与发电侧双方的利益，并非真正意义上的社会福利最大化模型。此外，文献[20]的算例分析没有设计算法，也没有与离散的社会福利最大化实时定价模型进行比较分析，不能体现出连续的社会福利最大化实时定价模型的优势。因此，本文在文献[20]的基础上，结合目前的智能电网实时定价策略与方法，综合考虑用户侧与发电侧双方的利益，继续完善连续的社会福利最大化实时定价模型的理论与推导；并且将该模型与离散的社会福利最大化实时定价模型进行比较分析。仿真实验结果表明本文所提连续的社会福利最大化模型不仅能够削峰填谷，有效地保证电力系统的供需平衡以及用户和供电商双方的利益，还能最大限度地避免发生峰谷转移的情况。

1 效用函数与成本函数理论

1.1 效用函数

在智能电网实时定价中，效用函数指用户对消耗一定电量的满意度，需要满足非递减性和边际效用递减2 个特征[21]。智能电网实时定价中的效用函数主要采用式（1）二次函数：

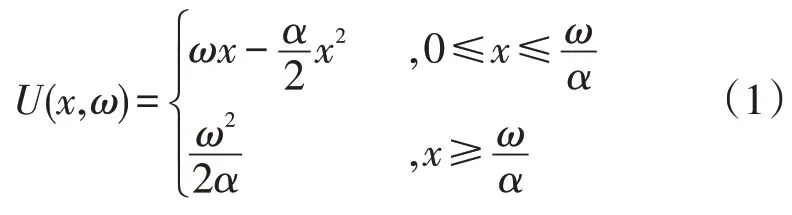
式中：α,ω均为常数，0 ＜α≤1，ω为用户的用电意愿；x为用户所需要的用电量。

1.2 成本函数

供电商发电系统中存在一定的成本，假设损耗成本和维修成本均很小，可以忽略不计，主要考虑发电系统的发电成本。

供电商的发电成本C可用二次函数[2-3，9，22]表示为：

式中：a＞0,b≥0,c≥0，且为常数；Q为发电量。

2 连续的社会福利最大化模型

2.1 电力系统概述

本文考虑1 个供电商的简化模型，用户侧有n个电器，且配有智能电表。

在考虑用电时间的连续性下，由(P(t),t)关系得到的电量可用黎曼积分表示为：

式中：P(t)为功率与时间的关系；P为用户电器的功率；w为用户的用电量；T为电器的使用时长；t为连续时间变量。

连续模型下用户的福利N(Pj(t))和供电商的利润R(Pf(t))分别为：

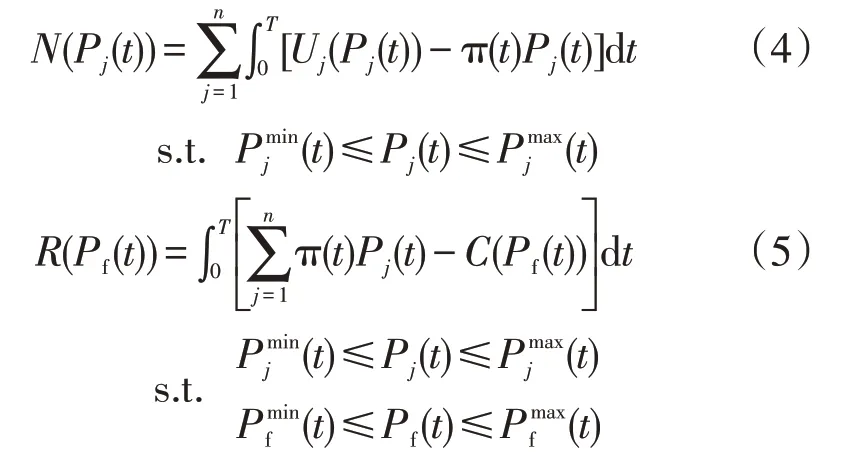
式中：π(t)为随时间变化的实时电价；Pj(t)为用户第j个电器的功率曲线；Pf(t)为供电商的发电装置的功率曲线；Uj(Pj(t))为用户使用电器j的效用；C(Pf(t)为供电商的成本；Uj为关于电器功率Pj(t)的泛函；C为关于发电功率Pf(t)的泛函；分别为第j个电器功率曲线的最小、最大功率；分别为发电装置的最小、最大功率；均为不随时间变化的常数。

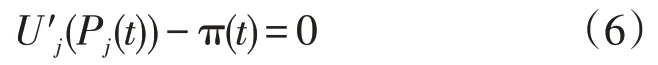
2.2 模型的建立

社会福利最大化理论同时考虑了用户侧和发电侧双方的利益，智能电网实时定价下的社会福利最大化模型通常是用户的效用减去供电商的成本[2-3，9-11，13，16，22-23]。类似于离散时间的实时定价研究，以功率平衡为约束条件，当0 ≤t≤T时，连续的社会福利最大化模型表示为：

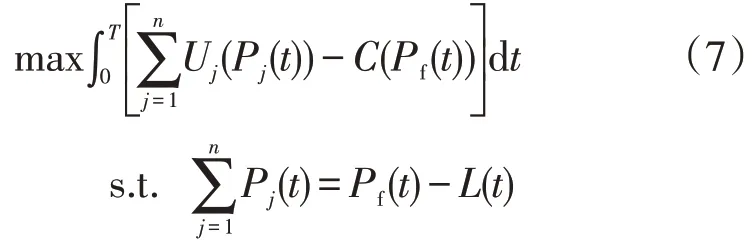
式中：L(t)为电路中的损耗；L(t)=γPf(t)，γ为损耗率。

模型（7）以Pj(t)，Pf(t)为决策变量对用电和供电进行优化，与现有模型[20]的区别在于模型（7）同时考虑了用户侧和发电侧双方的利益，是真正意义上的社会福利最大化模型；而文献[20]只考虑了发电侧的成本最小化，不是真正意义上的社会福利最大化模型。相同之处在于模型（7）也是泛函问题，所以，变分问题（7）的求解转化为泛函极值优化问题，求解方法为Euler-Lagrange 方程[20-21]。因此，首先引入拉格朗日乘子λ(t)，定义模型（7）的广义泛函为：

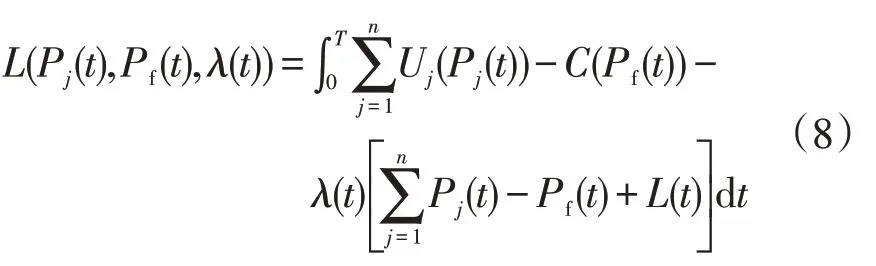
然后可得到变分问题式（8）的Euler-Lagrange方程为：

比较式（6）和式（10）可知：

证明了式中的λ(t)也为实时电价。

此外，式（10）还可以表示所有用电器的边际效用相等；由式（10）—式（11）可知，U′j(Pj(t))=C′(Pf(t))，表示边际效用等于边际成本，是经济学上著名的生产定律。理论上，由式（10）可得：

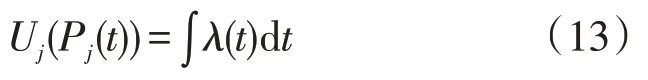
考虑到复杂的泛函不易求解，Pj(t)也可由式（14）求解。

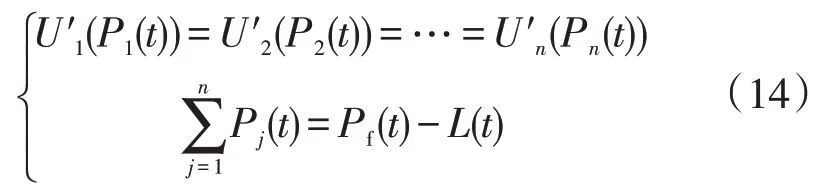
即通过Pj(t) (1 ≤j≤n)之间的关系，再结合功率平衡条件，即可求解出用电器的最优功率Pj(t)。同理，若发电侧有多个发电厂，每个发电厂的最优发电功率亦可用此方法求解。

基于连续的社会福利最大化模型的实时定价策略主要通过求解出用户最优的功率曲线、供电商最优的发电功率曲线，进而求得最优的实时电价。在经济学上，通常用等微增率准则来进行最优负荷的经济分配。

2.3 模型的解析解

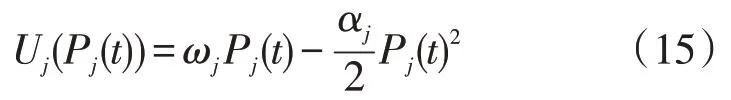
式中：αj,ωj均为常数，0 ＜αj≤1；ωj为用户的用电意愿；Pj(t)为第j个电器的功率。

考虑发电时间连续性的发电成本可用二次函数来表示[24-25]，即

在连续的社会福利最大化模型中，考虑用户的效用尚未达到饱和的情况下的效用函数，可得：

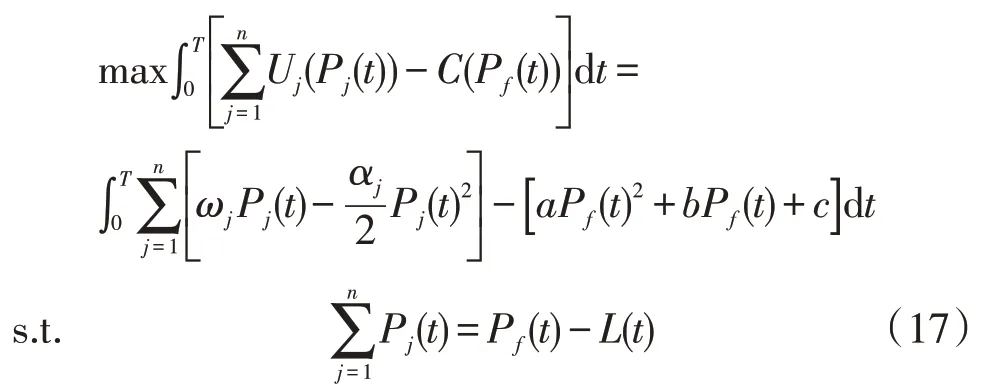
由式（10）和式（11）可得：

由式（18）可知，λ(t)与j无关，所有电器的价格是相同的。式（19）的结果与文献[20]的单边竞价模型结果一致，不同的是λ(t)还可以根据式（18）来求解，因此社会福利最大化模型中的2 个决策变量Pj(t),Pf(t)还需要满足以下条件：

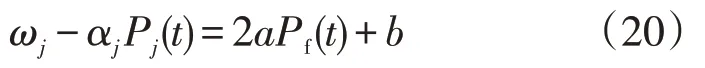
将Pf(t)代入功率平衡约束可以得到：

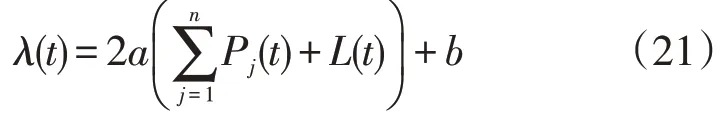
由式（21）可知，电价λ(t) 与负荷曲线Pd(t)=一致，即用电量需求越高，电价越高，从而可以考虑通过价格信号来引导用电行为的方式进行削峰填谷。

由式（10）可得：

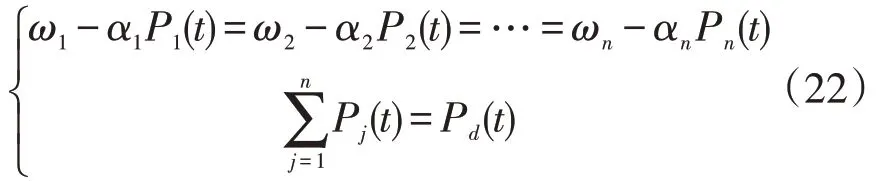
由式（22）可以求出Pj(t)。代入式（18）可以得到

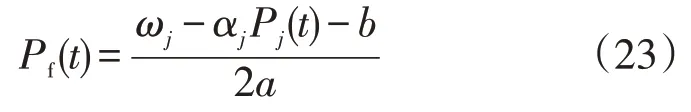
最后把Pj(t),Pf(t)回代到式（18）或式（19）即可求解出电价λ(t) 。

此外，从连续的社会福利最大化模型式（17）可知，当Pj(t)，Pf(t)是不随时间t变化的常函数时，即功率在这段时间内是均匀变化的，此时连续的社会福利最大模型可看成是离散的社会福利最大化模型，离散的定价方法也同样适用。

3 模型的求解算法

实时定价是用户和供电商双向互动的过程[4]，双方通过智能电表进行信息交流。用户根据供电商提供的电价，结合自身的效用最大化进行用电决策，包括是否用电以及用电量的多少等，并将决策信息通过智能电表反馈给供电商。供电商根据成本最小化进行供电决策，并通过智能电表向用户发布电价信息，接收用户的反馈信息以及发送供电量信息。

算法的设计以用户和供电商双方的信息交流为基础，相比于离散的模型，连续模型的最大不同之处在于其每时每刻都可变，可以随时进行调整。因此，在模型的求解算法上也会有所不同。

当0 ≤t≤T时，本文建立的连续的社会福利最大化模型的算法步骤为：（1）数据初始化；（2）由式9—式11）得出Pj(t)之间的关系，以及Pj(t)与Pf(t)之间的关系；（3）赋初始值Pj(t)；（4）设定损失率γ，由=Pf(t)-L(t) 求解出合适的初始值Pf(t) ；（5）判断U′j(Pj(t))=C′(Pf(t))是否成立，若不成立，转（3）至（5）；若成立，则转（6）；（6）由式（10）或式（11）求得λ(t)；（7）得到初始λ(t)后，根据式（24）预测下一时刻的Pj(t)与Pf(t)；（8）重复（5）至（7）直至结束。

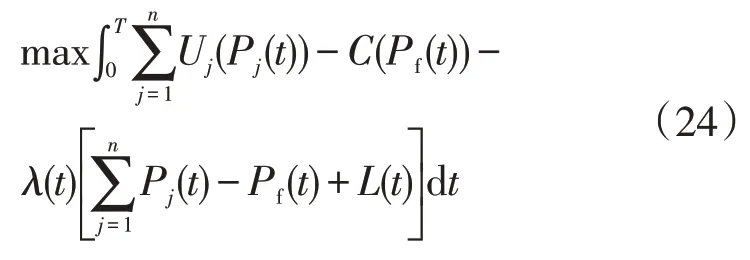
4 仿真分析

4.1 参数设置

通过仿真实验验证本文所提模型的合理性与有效性。假设电力系统是由1 个供电商和用户组成的简化模型，同时将用户侧看成1 个整体，假设用户侧有2 个用电器，即j=2。其他参数分别设置为：ω2=2ω1,α2=2α1,γ=0.03,L(t)=0.03Pf(t)，a=0.01,b=c=0。假设供电商根据负荷曲线进行规划发电，用户根据负荷曲线进行规划用电。通过Matlab2019b进行仿真分析。

4.2 结果分析

连续模型下负荷曲线、发电和损耗之间的关系如图1 所示。

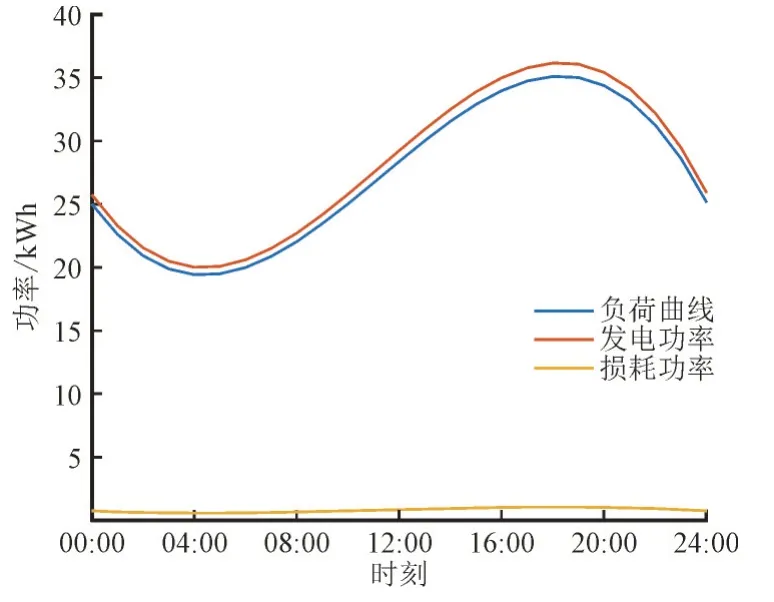
图1 连续模型中负荷曲线、发电功率和损耗之间的关系Fig.1 Relationship among load curve，generated power and loss in continuous model

由图1 可知，1∶00—6∶00 属于用电低谷期，7∶00—18∶00 属于用电高峰期，19∶00—24∶00 的用电处于用电低谷期和峰期之间，符合用户的作息习惯。此外，连续模型下的供电商的发电功率曲线与用户的负荷曲线之间的趋势基本相同，发电功率曲线稍高于电器的负荷曲线，说明了发电量能够满足用户的需求，同时也不会造成过多的电力浪费。

图2 为连续模型中负荷曲线和电器功率分配的具体情况。由图2 可知，连续模型下用户侧2 个电器功率的功率曲线，其中，电器1 与电器2 的总功率即负荷曲线，且电器1 与电器2 各自的功率曲线与负荷曲线在趋势上也大致相同。电器1 与电器2 的功率曲线均比较平缓，最高点与最低点之间的差值不大，表现出较好的削峰填谷效果。

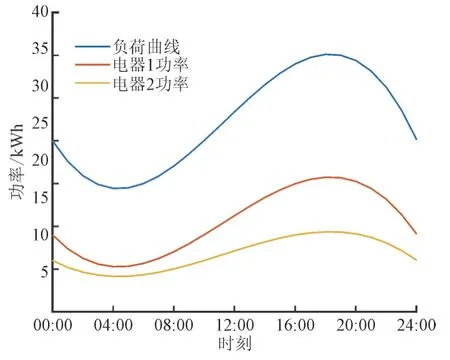
图2 连续模型中负荷曲线和电器功率分配Fig.2 Load curve and appliance power distribution in continuous model

图3 为连续模型得到的最优实时电价。由图3可知连续模型下的实时电价的波动情况与图2 中的负荷曲线的趋势相似。证明了当用电需求下降时，电价也随之下降，以激励用户多用电；当用电需求上升时，电价也随之上升，以减少用户在此时的用电。实时定价的目的主要是通过价格机制来引导用电行为，从而实现削峰填谷的目标。

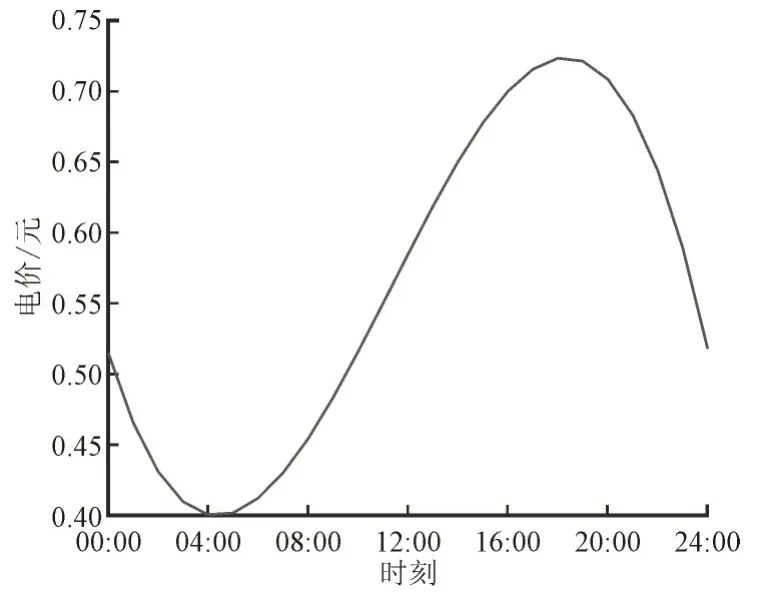
图3 连续模型的实时电价Fig.3 Real-time electricity prices in continuous model

图4 为连续模型下的社会福利与成本。由图4可知社会福利曲线位于成本曲线上方，说明同时考虑了供电商和用户双方利益的社会福利最大化模型得到的平均福利要优于仅仅考虑了供电商单侧的成本最小化模型得到的平均福利。因此验证了连续的社会福利最大化模型在智能电网实时定价中的合理性与有效性。

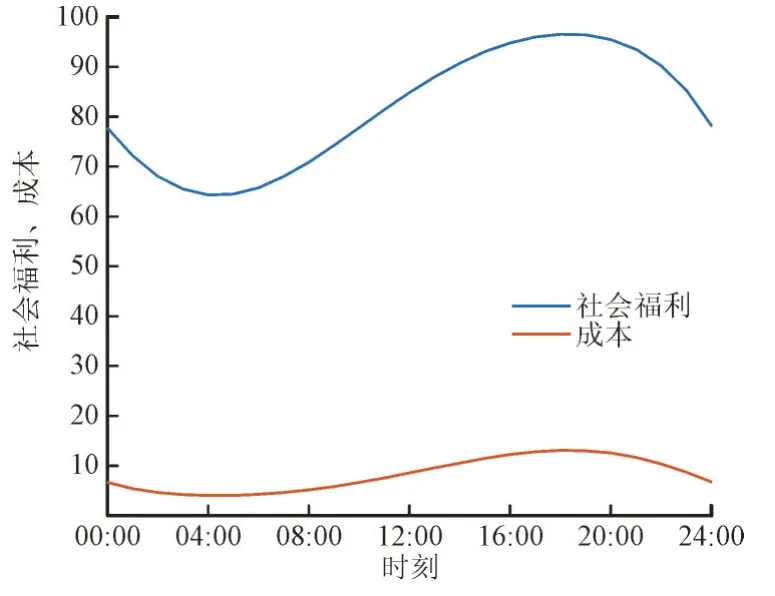
图4 连续模型中的社会福利与成本Fig.4 Social welfare and cost in continuous model

图5 为供电商分别在连续、离散模型中的发电功率情况。由图5 可知，在离散的模型下，供电商不能即时对发电功率进行调整，为了满足用户的用电需求，电力系统的发电量为负荷曲线在交易时长内的最大负荷；而连续的模型可以随时对发电功率做出调整，故连续模型下的发电功率可以看成近似于负荷曲线。由于发电量可表示为发电功率曲线与坐标横轴所围成的面积，因此，在同一段时间内，离散模型下的发电量高于连续模型下的发电量，容易导致供过于求的情况，同时消耗着较大比例的电力资源和成本。

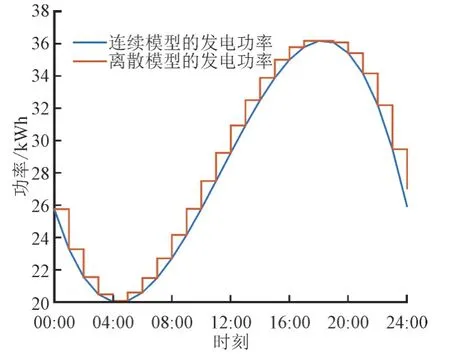
图5 连续、离散模型中的发电功率Fig.5 Electricity generation in continuous and discrete model

图6 为用户分别在连续、离散模型中的用电功率情况。由图6 可知，当负荷曲线上升时，离散模型下用户在用电时长T内的电器功率为负荷曲线在该时间段内的最小功率；当负荷曲线下降时，离散模型下用户在用电时长T内的电器功率为负荷曲线在该时间段内的最大功率。由于连续的模型可以通过随时改变用电功率，则这种情况下的电器功率曲线近似于负荷曲线。

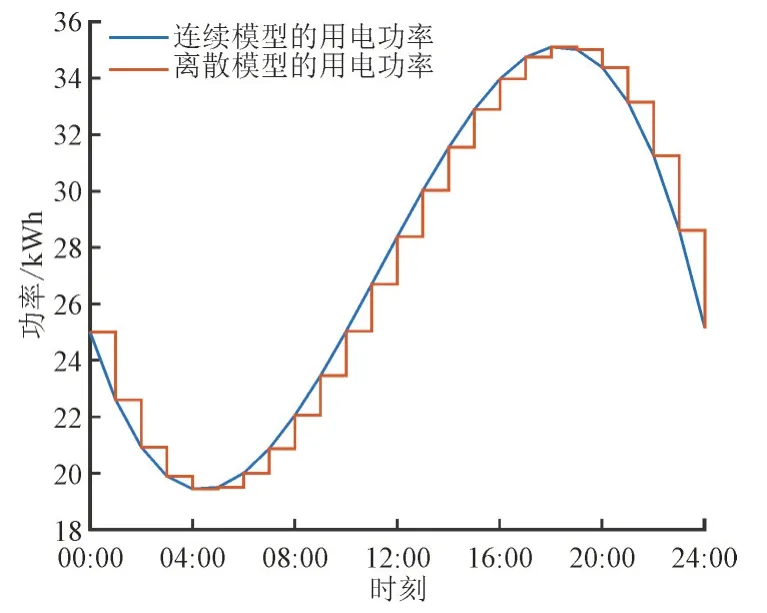
图6 连续、离散模型中的用电功率Fig.6 Electricity consumption in continuous and discrete model

图5—6 表明了不管是连续的模型下还是离散的模型下，发电功率曲线均与用电功率曲线的趋势相同，都保证了用户的用电需求。同时，如果同一段时间内要将功率从相同的初值变成相同的终值，连续的模型可以随时对发电和用电功率做出调整，缓慢地改变，也给发电装置和电器预留了适当的缓冲时间，保证电路的安全运行。而离散模型下不能马上调整发电、用电功率，且会在可以发生调整的固定时刻使得功率从初值立刻变为终值，整个过程中没有给发电装置和电器预留任何的缓冲时间，容易导致电路的不稳定。图7 为在连续、离散模型下的社会福利。

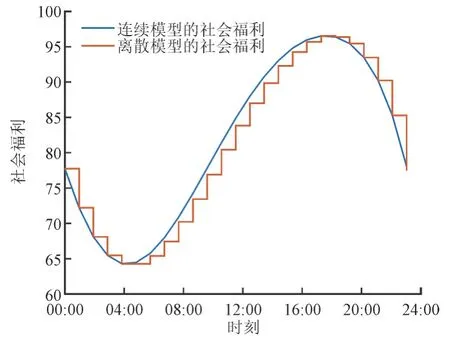
图7 连续、离散模型中的社会福利Fig.7 Social welfare in continuous and discrete model

图5—7 主要是为了研究社会福利最大化模型在连续、离散情况下的区别。通过比较分析可知，基于连续的社会福利最大化模型的成本更低，但并非所有的指标都优于离散的社会福利最大化模型。在一段时间内，由于离散的模型在划分好的一段时间内的发电量和用电量是固定的，不能迅速改变，这就很大可能会形成新的峰谷期。而连续的模型可以通过实时电价的迅速改变从而迅速调节用电器的功率，可以更及时地进行削峰填谷。因此，连续的社会福利最大化模型的最大优点主要在于调节的灵活性。同时，图5—图7 也验证了连续的社会福利最大化模型下的实时定价方法的合理性与有效性。

5 结论

在智能电网实时定价的社会福利最大化方法中，现有的定价模型基本都是离散的，没有侧重体现发电和用电的时间连续性这一重要特征对实时定价的影响。本文将发电和用电的时间连续性融入到智能电网实时定价中，建立了连续的社会福利最大化模型，在理论上推导出了实时电价与发电功率、用电功率之间的关系，并设计了求解模型的算法。通过与离散的社会福利最大化模型的比较分析，得到如下结论：

1）连续的社会福利最大化模型不仅能够有效地削峰填谷，还能保证电力系统的供需平衡以及用户和供电商双方的利益。同时，以社会福利最大化为目标函数带来的社会福利要高于以供电商成本最小化为目标函数带来的社会福利。

2）在连续和离散的社会福利最大化模型的比较中，前者不仅能够有效地降低发电成本，还能凭借其每时每刻都能发生变化的优势及时灵活地调节用电的峰谷期，最大限度地避免发生峰谷转移的情况。证明了连续的社会福利最大化模型应用于智能电网实时定价中的合理性与有效性。