弯曲波-纵波彩虹捕获效应及其模式转换

徐艳龙，王芳隆，沈一舟，杨智春

（1.西北工业大学深圳研究院，广东 深圳 518057；2.西北工业大学航空学院，陕西 西安 710072）

近些年来，可以实现弹性波操控的人工结构，如声子晶体与超材料［1］，声镜［2］，声学黑洞［3］等，引起了研究者的广泛关注。而宽带弹性波在梯度人工结构中传播时会发生彩虹捕获效应，即不同的频率的弹性波会在结构的不同位置停止向前传播并发生能量聚集，这种梯度人工结构被称为彩虹捕获结构［4-5］。它是Tsakmakidis等［6］于2007年在电磁波领域首次提出的，后来相关研究人员通过设计具有梯度色散关系的子胞来实现彩虹捕获效应，这种效应很快被推广到了声学领域。在声学领域［7-10］，研究者主要关注基于彩虹捕获效应的传感和滤波［8］、宽带吸声［9］以及彩虹捕获结构的微型化和低频化［10］。

2015年Xu等［4-5］首次将彩虹捕获效应应用到弹性波领域，研究了瑞利波和水平剪切波（SH波）的彩虹捕获效应。在此之后，关于弹性波彩虹捕获效应的研究按照研究侧重点可以分为两类：第一类主要实现各种弹性波（兰姆波、表面波、SH波等）的彩虹捕获效应［11-13］；第二类主要关注弹性波彩虹捕获效应的应用，如基于此效应的能量俘获［14］、模式转换［15-19］等。模式转换是指弹性波在传播的过程中极化方向发生改变的现象。Colombi等［15］在置于弹性半空间表面的共振梯度结构上，最先发现了基于彩虹捕获效应的瑞利波到体剪切波的模式转换；他们在随后的研究工作［16］中对相关现象进行了实验验证。Skelton等［17］在流体载荷作用下的梯度结构板中，发现了弯曲波到流体中体波的模式转换。Ponti等［18］设计了一根不具有几何对称性的梯度结构梁，发现了该结构发生彩虹捕获效应时从入射的弯曲波到反射的扭转波的模式转换。

作为弹性波操控领域一个正在兴起的研究方向，国内外关于基于弹性波彩虹捕获效应的模式转换的研究才刚刚起步。目前仅实现了从瑞利波向体波，从弯曲波向扭转波的转换。更多的现象、机理和应用等待研究者去探索。本文提出了一种梯度结构梁，通过传递矩阵法解析求解了子胞的能带结构，并利用有限元法验证了其准确性，根据子胞的能带结构从波数变化的角度，解释了弯曲波-纵波彩虹捕获效应及其模式转换的产生机理。通过有限元频域仿真，验证了弯曲波-纵波彩虹捕获效应，并通过有限元时域仿真，验证了彩虹捕获效应发生时弯曲波和纵波的双向模式转换。

1 梯度结构梁子胞的能带结构

1.1 梯度结构梁

本文设计的可以实现弯曲波-纵波彩虹捕获效应的梯度结构梁如图1所示，其由1个基梁（图中灰色部分）和16个高度梯度变化的立柱（图中黑色部分）组成。可以将梯度结构梁划分为16个子胞，第1个子胞的立柱高度为H=2.0 mm，第n个子胞的立柱高度为Hn=H+（n－1）h，其中h=0.2 mm。基梁的厚度T和立柱的厚度b都是2 mm；基梁和立柱的宽度都是20 mm；梯度结构梁的晶格常数D是12 mm。材料选用光敏树脂，其弹性模量Y为2.067 8 GPa，密度ρ为1 110 kg·m－3。

图1 梯度结构梁Fig.1 Beam with graded pillars

1.2 能带结构的求解

由于梯度结构梁的立柱高度增量比较小，因此可借鉴研究周期结构（即声子晶体）中弹性波传播的方法来研究梯度结构梁中弹性波的传播。为了分析彩虹捕获效应的产生机理，以及预测彩虹捕获效应在梯度结构梁中的发生位置和相应的频率范围，首先要得到相应的周期结构梁子胞的能带结构［4，12］。本文基于Cao等［19］的研究，通过传递矩阵法解析求解子胞的能带结构。任取图1中所示的梯度结构梁的一个子胞作为相应周期结构梁的一个子胞，并利用中性轴将子胞进行简化，如图2a所示。

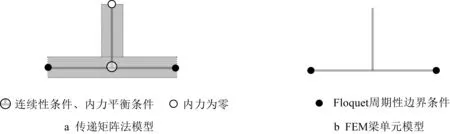
图2 用于计算能带结构的传递矩阵法子胞模型和有限元法（FEM）子胞模型Fig.2 Transfer matrix method model and finite element method(FEM)model of subunit used to calculate band structure

由于基梁和立柱的相互作用，子胞中同时存在弯曲波和纵波。从梁中的弯曲波和纵波的控制方程出发，结合以下三个力学条件：①立柱与基梁连接的结点处满足连续性条件；②立柱与基梁连接的结点处满足内力平衡条件；③立柱的上端面满足内力为零的边界条件，可以得到：

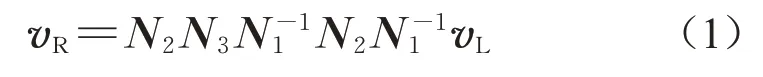
式 中：vR=[wR，uR，φR，FR，VR，MR]T和vL=[wL，uL，φL，FL，VL，ML]T，分别为基梁的右端面状态向量和左端面状态向量。其中，w为挠度，u为轴向位移，φ为转角，F为轴力，V为剪力，M为弯矩。下标R和L分别代表基梁的右端面和左端面，上标T表示矩阵的转置。N1、N2和N3为传递矩阵，它们的具体形式分别如式（2）—（4）所示，推导过程可以在参考文献［19］中找到。

对于周期结构梁，单个子胞具有周期性，子胞的基梁两端的状态向量满足Floquet周期性边界条件（也称作Bloch边界条件），即：

式中：k为Bloch波数。

联立方程（1）和（7），可以得到一个特征值方程：

式中：E为六阶单位阵。

求解方程（8），就可以得到在周期结构梁中传播的弹性波频率f和波数k之间的关系曲线，即色散曲线。这些色散曲线构成了子胞的能带结构。色散曲线的斜率代表了结构中可以传播的弹性波的群速度。

为了验证传递矩阵法解析解的正确性，本文在有限元软件COMSOL中建立了梁单元的子胞，如图2b所示。图3中展示了立柱高度分别为1.0 mm和50.0 mm的子胞在不可约布里渊区［0，πD-1］内的能带结构（图中横轴表示的物理量为归一化波数kDπ-1，其量纲为1）。黑色实心三角形点代表通过传递矩阵法求得的解析解，黑色空心正方形点线代表通过梁单元得到的有限元解。可以看出，传递矩阵法解析解与有限元法梁单元解完全重合。

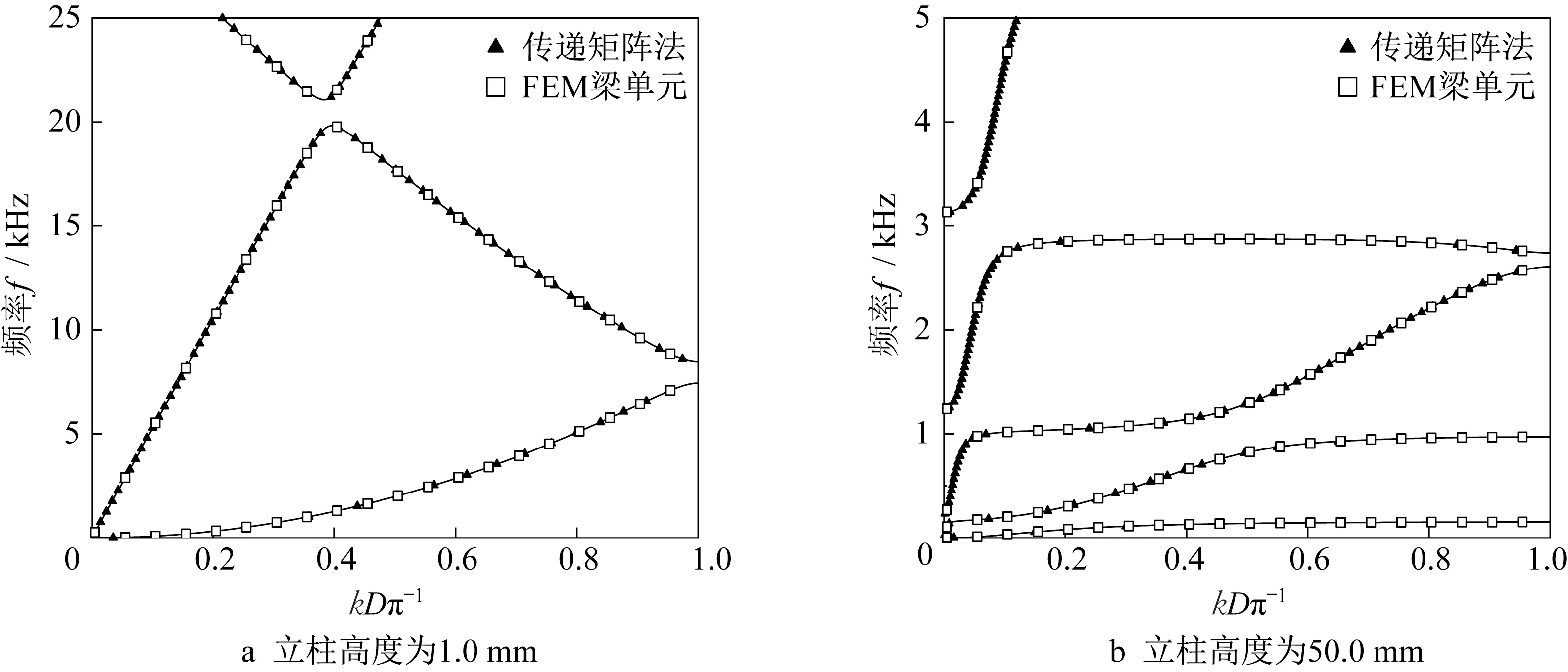
图3通过传递矩阵法和有限元法得到的能带结构图的对比Fig.3 Comparison of band structures obtained by transfer matrix method and finite element method

1.3 能带结构的分析

图4 中黑色圆形点线表示立柱高度H1=2.0 mm的子胞在0～25 kHz范围内的能带结构。图中，Vg表示群速度。为了便于对比，图中也绘出了均匀梁中弯曲波和纵波的色散曲线，分别用黑色实线和黑色点划线表示。由图可知，子胞能带结构的前两阶色散曲线和均匀梁的色散曲线的走势大部分保持一致。仿照文献［12］中的提法，将子胞的能带结构中与均匀梁的弯曲波色散曲线走势一致的部分称为伪弯曲波模式色散曲线，与均匀梁的纵波色散曲线走势一致的部分称为伪纵波模式色散曲线。从图4中也可以看出，子胞中伪弯曲波模式和伪纵波模式的波形分别与均匀梁中的弯曲波模式和纵波模式的波形非常相似。但是需要注意的是，子胞中伪弯曲波和伪纵波模式与均匀梁中的弯曲波和纵波模式是有所区别的。首先，均匀梁的色散曲线是不间断的，即在任何频率下都会有相应的弯曲波和纵波模式存在。而子胞的色散曲线在某些频率段是间断的，如图4中灰色区域所示的既没有伪弯曲波模式又没有伪纵波模式的弯曲波-纵波全带隙。在此带隙内子胞中不存在任何模式，子胞的基梁中当然也不会存在任何模式。其次，当子胞的立柱较高时，立柱的共振会与基梁中的波耦合在一起，虽然此时子胞的色散曲线与均匀梁的色散曲线走势还保持一致，但子胞基梁中的波形与均匀梁中的波形相差比较大。

图4 立柱高度为2.0 mm的子胞能带结构Fig.4 Band structure of the subunit with a pillar height of 2.0 mm

另外，在图4中，子胞的二阶色散曲线上存在一个特殊的点：伪弯曲波模式与伪纵波模式色散曲线的分界点，此点所对应的频率是弯曲波-纵波全带隙的下边界。同时，此点所对应的群速度为0（Vg=0），因此将其称为零群速度点。零群速度点处的模式既非伪弯曲波模式，也非伪纵波模式，而是耦合模式，其波形介于伪弯曲波模式波形和伪纵波模式波形之间。梯度结构梁中16个子胞的立柱高度是渐变的，故其二阶色散曲线和零群速度点也是渐变的。这就会导致弯曲波-纵波彩虹捕获效应及其模式转换的发生。

2 彩虹捕获效应及模式转换机理

本文将图1所示的16个子胞的二阶色散曲线依次绘制在一张图中，并利用波矢量的周期性对能带结构做第二布里渊区的扩展，如图5所示，其中k∈［-2πD-1，0］代表波的反向传播。各子胞的二阶色散曲线（IV区域中箭头所指的1～16）由黑色曲线表示。子胞的立柱高度越大，其色散曲线频率就越低。灰色实线和灰色点划线分别代表均匀梁中的弯曲波和纵波的色散曲线；黑色水平虚线为一条等频率线，代表待分析的入射波的频率。

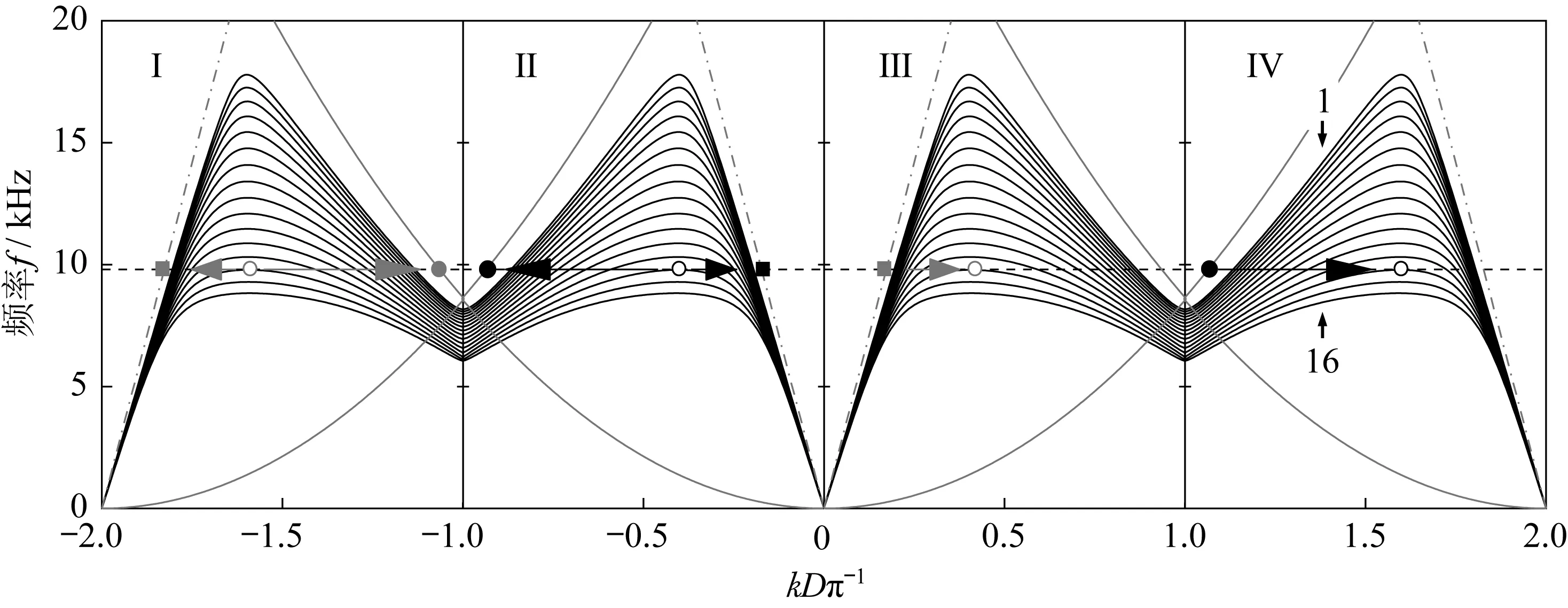
图5 弯曲波-纵波彩虹捕获效应及其模式转换机理Fig.5 Mechanism of flexural-longitudinal wave rainbow trapping and its mode conversion

在图5的Ⅳ区域中，等频率线与均匀梁中的弯曲波色散曲线相交于黑色实心圆点，这意味着入射的弯曲波在均匀梁中以黑色实心圆点所对应的波数进行传播。弯曲波从均匀梁中传进梯度结构梁后，遇到的子胞的立柱高度越来越大，等频率线与色散曲线的交点沿着黑色箭头逐渐从立柱高度较小的子胞色散曲线上移动到立柱高度较大的子胞色散曲线上，对应的波数也逐渐变化，其模式逐渐从均匀梁的弯曲波模式转变为梯度结构梁子胞中的伪弯曲波模式。在这个过程中，其群速度越来越小。沿着黑色箭头，黑色水平虚线与第14个子胞的色散曲线相切于黑色空心圆点。此时其模式为耦合模式。此处色散曲线的斜率为0，这说明波的群速度变成了0。由于波动量的守恒，零群速度的波将会反向传播，波数k将会变为k-2πD-1，即此时Ⅳ区域中的黑色空心圆点转变成了Ⅱ区域中的黑色空心圆点。在反向传播的过程中，反射波遇到的子胞的立柱高度越来越小，其模式逐渐从耦合模式转变为子胞中的伪纵波模式和伪弯曲波模式。沿着黑色箭头，最终等频率线分别与均匀梁中的纵波色散曲线和弯曲波色散曲线相交于黑色实心方点和黑色实心圆点。这代表着反射波在传出梯度结构梁后，最终转变为均匀梁中的纵波和弯曲波。即在这个过程中，完成了从弯曲波到纵波的模式转换。

同样，通过梯度结构梁也能实现从纵波到弯曲波的模式转换。在图5的Ⅲ区域中，等频率线与均匀梁中的纵波色散曲线相交于灰色实心方点。这代表着入射的纵波，在均匀梁中以灰色实心方点所表示的波数进行传播。纵波从均匀梁中传进梯度结构梁后，遇到的子胞的立柱高度越来越大，等频率线与色散曲线的交点沿着灰色箭头逐渐从立柱高度较小的子胞色散曲线上移动到立柱高度较大的子胞色散曲线上，对应的波数也逐渐变化，其模式逐渐从均匀梁的纵波模式转变为梯度结构梁子胞中的伪纵波模式。在这个过程中，其群速度越来越小。沿着灰色箭头，黑色水平虚线与第14个子胞的色散曲线相切于群速度为0的灰色空心圆点。此时其模式为耦合模式。由于波动量的守恒，在反射时，波数k将会变为k-2πD-1，这时Ⅲ区域中的灰色空心圆点转变成了Ⅰ区域中的灰色空心圆点。在反向传播过程中，反射波遇到的子胞的立柱高度越来越小，其模式逐渐从耦合模式转变为子胞中的伪弯曲波模式和伪纵波模式。沿着灰色箭头，最终等频率线分别与均匀梁中的弯曲波色散曲线和纵波色散曲线相交于灰色实心圆点和灰色实心方点。这代表着反射波在传出梯度结构梁后，最终转变为均匀梁中的弯曲波和纵波。

通过本节的以上分析也可以知道，如果入射波是宽带的，那么不同频率成分的入射波将会在不同的子胞处达到零群速度，即会在结构中不同的位置处停止向前传播而发生反射。频率越低，对应子胞的立柱越高，发生反射的位置越靠后。这样就产生了弯曲波-纵波彩虹捕获效应。入射弯曲波在发生弯曲波-纵波彩虹捕获效应后，反射波中会存在纵波；入射纵波在发生弯曲波-纵波彩虹捕获效应后，反射波中则会存在弯曲波，即弯曲波-纵波彩虹捕获效应发生时会伴随着模式转换。为了直观地将弯曲波-纵波彩虹捕获效应的发生位置与入射波频率对应起来，本文把第n个子胞的二阶色散曲线的零群速度点所对应的频率（简称为零群速度点频率）fn和两相邻子胞的零群速度点频率fn和fn+1的中间频率fn，n+1列在表1中，后文中将以fn，n+1作为仿真的入射波频率。

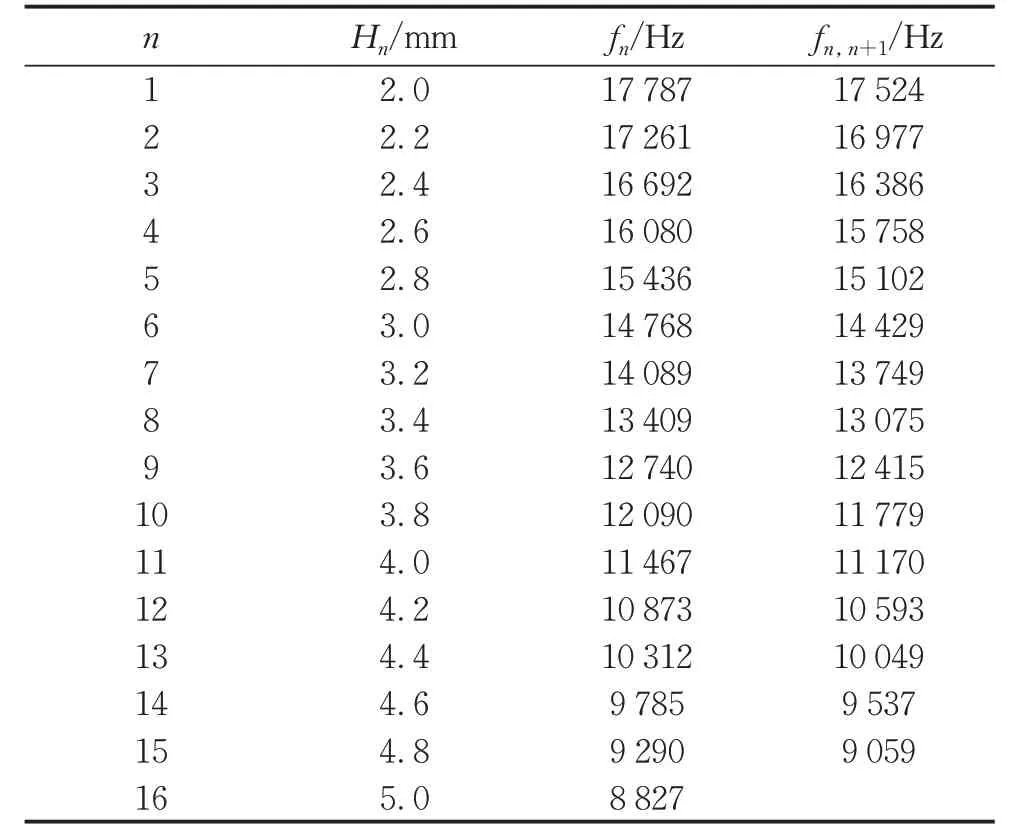
表1 子胞零群速度点频率fn和两相邻子胞零群速度点频率的中间频率fn，n+1Tab.1 Frequency corresponding to point of zero group velocity of subunit and average frequency of points of zero group velocities of two adjacent subunits

3 彩虹捕获效应及模式转换有限元仿真

基于第2节中所阐述的机理，本文在COMSOL中进行仿真分析，通过频域仿真验证彩虹捕获效应，通过时域仿真验证模式转换。

3.1 频域仿真与彩虹捕获效应

本文在COMSOL中建立的模拟彩虹捕获效应的有限元仿真模型如图6所示。通过在线源处施加各个中间频率fn，n+1的z向激励以产生相应频率的弯曲波。通过在结构两边加合适长度的完美匹配层（PML）吸收传播到边界处的弯曲波，从而避免边界产生反射波扰乱波场。图7是不同频率下基梁中的z向归一化位移场（|w|）。可以看出彩虹捕获效应：不同频率的入射波传播到对应的子胞位置后，幅值分别迅速减小至零。

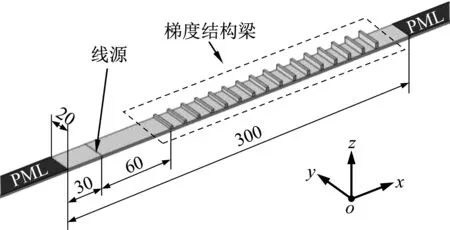
图6 有限元频域仿真模型（单位：mm）Fig.6 Finite element simulation model in frequency domain(unit:mm)

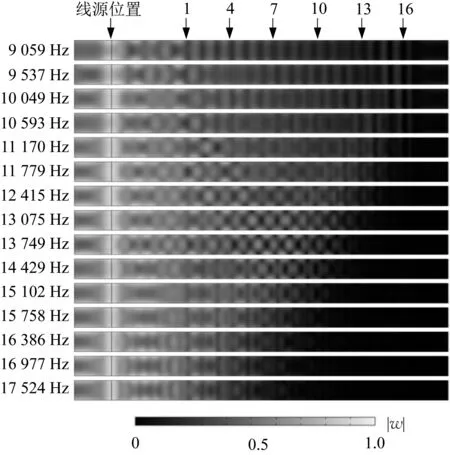
图7 彩虹捕获效应Fig.7 Rainbow trapping

3.2 时域仿真与模式转换

本节将进行有限元时域仿真，通过波在梯度结构梁中传播时的z向位移幅值与x向位移幅值时间历程云图，验证弯曲波-纵波彩虹捕获效应的模式转换。由于COMSOL时域仿真中没有完美匹配层设置，因此通过加长梯度结构梁两端的均匀梁长度，并让仿真时间小于弯曲波传播到边界所需的时间，来避免弯曲波在边界的反射。仿真中在线源处施加的位移载荷为5-cycle tone burst函数，其时域表达式如式（9）所示：

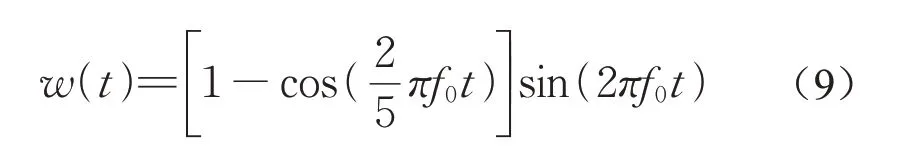
式中：f0为5-cycle tone burst函数的中心频率。

图8a为中心频率f0=13 075 Hz的弯曲波作为入射波在梯度结构梁中传播的时间历程云图。

图8 入射弯曲波向反射纵波的模式转换Fig.8 Mode conversion of incident flexural waves to reflected longitudinal waves

其中左半部分为梁表面的z向归一化位移幅值|w|的时间历程，右半部分为梁表面x向归一化位移幅值|u|的时间历程。以0.3t0（t0=1/f0）为时间步长分别截取时域仿真结果中基梁的z向归一化位移幅值|w|云图和x向归一化位移幅值|u|云图，并将其按时间的先后顺序进行组合就得到了图8a。观察图8a，入射波的|w|很大。入射波在对应的零群速度位置附近停止向前传播并发生反射之后，反射波的|w|几乎为0，而|u|比较大。入射波和反射波波形分别如图8b和图8c所示，可以明显看出入射波和反射波的波形与波长都不同。另外，由于图8a中每两个云图（图中的小横条）之间的时间间隔相同，都是0.3t0。故不同云图中的同一波前连线的倾斜程度可以表征波速，连线越倾斜，波速越小，连线越平缓，波速越大。可以发现，在发生彩虹捕获效应后波速变大了。这是因为在同一波导中，纵波波速大于弯曲波波速。以上各种迹象表明，正向传播的弯曲波在发生弯曲波-纵波彩虹捕获效应后转换成了反向传播的纵波。

图9a为中心频率f0=13 075 Hz的纵波作为入射波在梯度结构梁中传播的时间历程云图，其中左半部分为梁表面的x向归一化位移幅值|u|的时间历程，右半部分为梁表面z向归一化位移幅值|w|的时间历程。观察图9a，入射波的|u|很大，而|w|几乎为0。反射波的z向位移幅值|w|很大，而|u|很小。入射波和反射波波形分别如图9b和图9c所示。入射波和反射波的波形、波长和波速都不同。以上各种迹象与图8正好相反，这说明正向传播的纵波在发生弯曲波-彩虹捕获效应后转换成了反向传播的弯曲波。

图9 入射纵波向反射弯曲波的模式转换Fig.9 Mode conversion of incident longitudinal waves to reflected flexural waves

4 结论

为了通过彩虹捕获效应实现工程结构中常见的弯曲波和纵波的双向模式转换，本文提出了一种由基梁和立柱组成的梯度结构梁。通过传递矩阵法解析求解了子胞的能带结构，并利用有限元法验证了其求解过程的正确性。根据子胞的能带结构，从波数变化的角度解释了弯曲波-纵波彩虹捕获效应及其模式转换的产生机理。通过有限元仿真，验证了弯曲波-纵波的彩虹捕获效应以及彩虹捕获效应发生时弯曲波和纵波的双向模式转换。

作者贡献声明：

徐艳龙：公式推导、机理分析、论文撰写及修改。

王芳隆：公式推导、有限元仿真、图片绘制及论文撰写。

沈一舟：文献引证及论文修改。

杨智春：理论指导及论文审定。