模式识别在机械自动化制造过程中的质量监控
黄 亮
(浙江联宜电机有限公司,浙江 东阳 322100)
0 引言
随着经济、技术的腾飞,机械自动化制造企业如雨后春笋般涌现,市场竞争日益加剧。如何确保及提高机械自动化制造过程中的产品质量,成为众多企业在残酷的市场竞争中提高竞争力的关键手段[1-2]。由于机械自动化制造工序环环相扣,为避免机械自动化制造过程中产生的细小错误影响产品质量,需加强监控机械自动化制造过程中的产品质量[3]。机械自动化制造过程中的产品质量监控是指将在机械制造过程中产生的有关产品质量数据信息进行提取及分析,依据这些数据信息监控机械自动化制造过程的运行状态、确保机械自动化制造的产品质量、监控制造过程有无异常及降低废品率等[4]。
近些年,有关机械自动化制造过程中的产品质量监控的研究越来越受到国内外学者的关注。周昊飞等[5]提出基于深度置信网络的产品质量监控方法,但其对繁杂产品质量管控的时效性不好;武颖等[6]提出基于数字孪生技术的产品质量监控方法,但该方法容易受环境变化的影响使产品质量不稳定。
当前,机械自动化制造过程中的质量监控技术以统计过程控制(statistical process control,SPC)为主。SPC控制图是机械自动化制造过程波动的图形描述,采用SPC控制图可对机械自动化制造过程中的潜藏异常状况进行监测,运行人员通过识别到的控制图模式变化,实时掌握制造过程中质量的波动情况,达到管控过程质量以及监控制造过程的目的[7]。因此,本文提出模式识别在机械自动化制造过程中的质量监控方法,提高机械自动化制造过程中的产品质量的识别精准度。
1 机械自动化制造过程中的质量监控
1.1 机械自动化制造过程中的质量检测环节
在机械自动化制造过程中,产品质量监控由产品质量管理和产品质量控制构成,产品质量监控环节如图1所示。

图1 质量监控环节
机械自动化制造过程中的产品质量监控环节包含了从用户提出产品质量要求到产品制造加工的各个环节[8]。产品质量控制以控制产品生产到实现的每个环节均能符合规定要求为目标,将缺陷控制在产生的早期并将其消除。
1.2 基于模式识别的产品制造过程质量监控
基于模式识别的机械自动化制造过程中产品质量监控流程如图2所示。

图2 机械自动化制造过程中的产品质量监控流程
机械自动化制造过程中的产品质量监控流程为:结合产品生产关键工序、选定好的目标制造质量特性以及确定机械自动化制造生产线,采用数字化测量仪采集机械自动化制造生产线质量数据,采集到的产品质量数据经提取、存储和判断后,通过SPC控制图以图像化形式展现机械自动化制造过程中的产品质量监控情况。绘制用于制造产品质量识别的SPC控制图,判断控制图是否出现异常,并绘制用于制造产品质量控制的SPC控制图,针对异常情况进行调整[9]。
1.3 基于SPC控制图模式识别的质量监控
SPC控制图的主要原理:在机械自动化制造过程中,产品的质量特性值一直处于偶然波动或异常波动状态,机械自动化制造过程追求的目标是无异常波动即稳态[10],原因是机械自动化在稳态下制造,能够保证产品质量,且机械自动化制造最为经济。
SPC控制图分为正常模式和异常模式。机械自动化制造过程可受控即为正常模式;其不受控,有异常因素存在即为异常模式,且该模式包括趋势、阶跃和周期3种模式,其中,趋势和阶跃模式分别包括向上和向下的2种模式。
SPC控制图中的分析用控制图和控制用控制图分别应用于机械自动化制造过程中的分析和控制阶段,不稳定状态常处于机械自动化制造过程的初期,需要实时监测并针对搜寻出的不稳定原因采取相应的调控措施,如通过对机械自动化制造过程的过程能力指数进行运算,使机械自动化制造过程实现稳定受控状态后,进入产品质量控制阶段,在该阶段,需对机械自动化制造过程中的产品质量数据依据一定的间隔进行采样并绘制实时控制图[11]。在机械自动化制造过程中有异常情况发生时,需重复分析阶段步骤,实时搜寻过程异常原因,并采取相应措施使机械自动化制造过程恢复稳定受控状态,以便机械自动化制造出稳定质量的产品。
1.3.1 质量控制图模式识别的混合模型
SPC控制图模式识别的混合模型由聚类过程和分类过程组成。聚类过程采用改进k-means算法提取SPC控制图的有效距离特征,该距离特征在识别时表示详细的SPC控制图模式。在分类过程,控制图模式的识别可利用多分类的支持向量机算法完成。
a.基于改进k-means的SPC控制图特征提取。
采用传统k-means算法进行SPC控制图特征提取时,用k描述控制图模式所呈现产品质量数据集合与聚类数量,真实产品质量数据特征决定k的数量,当具备控制图模式所呈现产品质量数据时,为将产品质量数据吸引到聚类中心,k-means算法可依据距离函数完成。任意选择k个聚类中心,运算种群内全部产品质量数据样本到聚类中心的距离[12],选择离聚类中心最近的产品质量数据样本进行分配后,再次计算每个聚类中心的产品质量数据样本数量。反复循环以上过程,当达到设定要求时停止计算。
基于k-means算法的产品质量数据聚类过程为:
①k值的数量由产品质量数据特征决定,设m和Zj(L)为产品质量数据集合和其聚类中心,且j=1,2,…,k,对产品质量数据到聚类中心的距离进行运算。
②用F(xi,Zj(L)),i=1,2,…,m,j=1,2,…,k描述原始化聚类中心。
③为使余下的产品质量数据就近分配到聚类中心,可采用欧氏距离方法实现,假定满足一定条件为
D(xi,Zj(L))=min{D(xi,Zj(L))}
(1)
④新的聚类中心的均值采用产品质量数据聚类中心的均值,其公式为
(2)
⑤用G(l-1)描述上次更新处理的均值,令l=l+1,运算新的产品质量数据聚类中心Zj(L+1),其公式为
(3)
当全部产品质量数据被重新分配到不同的聚类中心时,则到达计算停止条件。
传统的k-means算法频繁得到局部最优解,原因是其对原始聚类中心存在敏感问题,以致聚类结果不够精确。为此,可结合k-means算法和粒子群算法,获得改进的k-means算法。采用k-means算法计算粒子群算法中的子代产品质量数据样本,获得局部最优解,并将采用的这些产品质量数据样本继续更新处理,使算法快速收敛,获得全局最优解。
将采用k-means算法获得的产品质量数据特征聚类中心,作为粒子群算法的原始粒子对机械自动化制造过程中的产品质量数据集进行分类,粒子群算法的步骤为:
①原始化粒子群的相关参数。设置机械自动化制造过程中的控制图模式所呈现产品质量数据的类型为c,即聚类中心数量为c,用X={v1,v2,…,vc}描述粒子位置,依据该位置和速度对产品质量数据聚类中心进行描述。
②采用k-means算法计算全部产品质量数据所在的聚类中心dij,计算公式为
(4)
其中,i=1,2,…,n,j=1,2,…,c。
③粒子的适应度值计算公式为
f(xi)=1/J(H,V)+1
(5)
H、V为粒子的位置和速度。
④更新粒子位置的公式为
(6)

⑤更新粒子群全局最优位置的公式为
(7)
⑥更新粒子移动速度与位置的公式为:
vid(i+1)=ω×vid(i)+(Hbest-xid(i))+
(gbest-xid(i))
(8)
xid(i+1)=xid(i)+vid(i+1)
(9)
ω为粒子权重;Hbest为产品质量数据粒子的最优位置;gbest为最佳产品质量数据的聚类中心。
⑦重复循环步骤②~步骤⑥的计算过程。若符合停止处理条件,则对机械自动化制造过程中的控制图模式的产品质量特征提取结果进行输出,采用欧氏距离法判断控制图模式的产品质量特征数据类型,完成机械自动化制造过程中的SPC控制图特征提取。
改进k-means算法完全关注到粒子群算法的全局最优解,可提高机械自动化制造过程中的SPC控制图特征提取效率。
距离特征是指在聚类过程内,利用改进k-means算法把初始的控制图模式产品质量数据集聚为k类,求解每个模式至不同聚类中心的欧氏距离[13]。在分类过程中输入提取出的距离特征。
用d(X,Y)描述欧氏距离,用X=(x1,x2,…,xp)T与Y=(y1,y2,…,yp)T描述产品质量数据的2个向量,其公式为
(10)
b.基于多分类支持向量机的控制图模式识别。
基于改进k-means算法提取到的SPC控制图特征,采用多分类支持向量机识别机械自动化制造过程中的产品质量控制图模式类型。该算法是在全部M类训练产品质量数据样本内对全部2类产品质量数据样本间构建支持向量分类器[14]。

用K(xi,xj)描述核函数,多项式核函数公式为
K(xi,xj)=[(xi·xj)+1]q
(11)
高斯核函数公式为
K(xi,xj)=exp(-|xi-xj|2/δ2)
(12)
式(11)和式(12)分别为全局性和局部性核函数;q和δ2为阶数和高斯核宽度。其中,式(11)的外推能力随着q降低而增强;式(12)的内推能力随着的δ2增大而减弱。式(11)和式(12)组合公式为
Kmix=aKpaly+Kgaussan
(13)
a∈(0,1)为混合参数,混合核函数具有优秀的学习和推广能力。
多分类支持向量机基于以上过程完成对机械自动化制造过程中的产品质量控制图模式类型的识别。
1.3.2 机械自动化制造过程中的质量监控的实现
由聚类过程和分类过程构成的控制图模式识别混合模型,可对机械自动化制造过程进行有效监控。聚类过程利用改进k-means算法降低机械自动化制造过程中的一个未知的控制图模式维度[15],同时进行优化训练。在分类过程中输入提取出的距离特征,采用训练好的SVM识别控制图模式类型,依据机械自动化制造过程信息和经验信息,对诊断出的异常因素进行调控。利用该混合模型进行控制图模式识别的流程如图3所示。
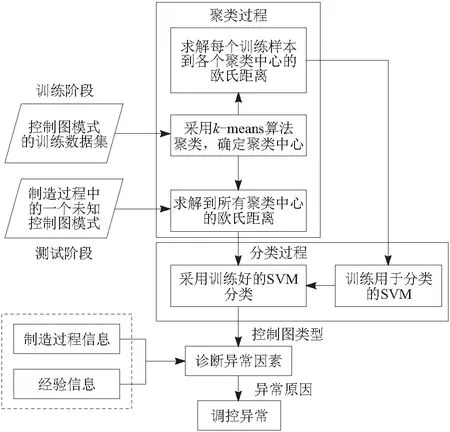
图3 控制图模式识别混合模型执行流程
2 实验分析
为验证本文方法对机械自动化制造过程中的质量监控性能,实验以某机械自动化制造厂为例,在MATLAB7.0与Libsvm环境下进行仿真实验。
实验为SPC控制图中的每种模式分别生成400个机械自动化制造过程中的产品质量数据样本,选择其中的200个作为训练产品质量数据样本,其余200个作为测试产品质量数据样本。分别将通过标准化处理后的训练产品质量数据样本的原始特征,与采用本文方法获得的距离特征先后作为分类过程的输入。SPC控制图的分类结果如表1所示。

表1 SPC控制图分类结果
由表1可看出,直接以机械自动化制造过程中的产品质量数据的原始特征作为输入,SPC控制图的识别精准度为92.80%,且阶跃与趋势模式的识别率较低;采用本文方法获得的机械自动化制造过程中的产品质量数据的距离特征作为分类过程的输入,识别精度大大提高,为99.88%,两者识别精准度相差7.08%,训练与测试时间均有所减少,且阶跃与趋势模式的识别率相对提高很多。实验表明,本文方法可有效提高SPC控制图对机械自动化制造过程中的产品质量数据的识别精准度,具有较高的识别性能。
实验采用本文方法对该机械自动化制造厂生成的齿轮尺寸进行监控,其中该齿轮的设计尺寸为58.000 mm,其最大和最小尺寸分别为58.231 mm、57.401 mm,现随机抽取8:00—8:30时间段的齿轮质量数据,并通过该厂自动生产线信息化系统界面对齿轮尺寸的监控结果进行展示,结果如图4和图5所示。

图4 质量监控界面
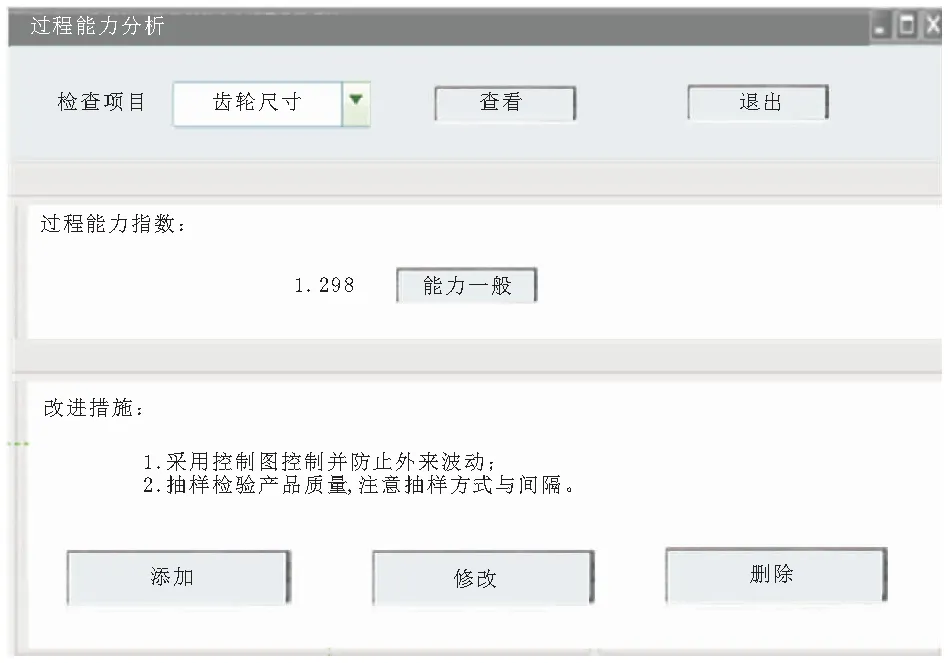
图5 过程能力分析结果
由图4可看出,采用本文方法对齿轮尺寸进行监控的整个过程中,机械自动化制造出的齿轮尺寸始终在设定的齿轮上下公差之内,且在8:15—8:30之间,齿轮尺寸曲线变化幅度较大,实际齿轮尺寸的最高值和最低值分别为58.202 mm、57.485 mm。
由图5可看出,基于以上的过程能力分析,本文方法监控到该机械自动化制造厂的制造的齿轮能力一般,本文方法可针对制造齿轮尺寸公差较大现象提出相应的处理措施,如在齿轮尺寸变化幅度较大的时间段对齿轮进行随机抽样检验等。综合图4和图5的实验表明,本文方法可对机械自动化制造过程中的产品质量进行有效监控,为确保机械自动化制造过程中的产品质量提供有利依据。
3 结束语
本文提出模式识别在机械自动化制造过程中的质量监控方法,经实验验证,通过对比以原始特征作为输入,将采用本文方法获得的机械自动化制造过程中,包含产品质量数据的SPC控制图模式的距离特征作为分类过程的输入,SPC控制图的识别精准度高达99.88%,两者识别精准度相差7.08%,且极大缩短训练与测试时间,说明本文方法可有效提高SPC控制图对机械自动化制造过程中的产品质量数据的识别精准度,具有较高的识别性能;通过对齿轮尺寸的实时监控,本文方法可有效监控机械自动化制造过程中的产品质量,为确保机械自动化制造过程中的产品质量提供有利保障。

