不确定因素下海上要地防空动态火力分配模型

王， 赵文飞， 滕克难， 周璐， 单鑫

(1.海军航空大学 岸防兵学院， 山东 烟台 264001； 2.92199部队， 山东 青岛 290014)

0 引言

海上要地是海军兵力栖息、休整、待机、补给和维修的根据地，是海军兵力生存和作战的依托，战时易成为敌空袭首要打击的目标[1-2]。在海上要地防空作战时，需要根据敌空袭兵器的出动规模以及我方防空武器装备组成进行合理的火力分配，以实现作战资源的最优配置，对提高防空兵的制空效能有着重要意义[3]。

火力分配(WTA)是将来袭目标分配给可用武器系统，以取得最大目标射击收益的过程，其中WTA问题又可分为静态火力分配(SWTA)与动态火力分配(DWTA)两类问题。传统的SWTA与时间无关，只针对来袭目标一次攻击进行一次火力分配。但在实际海上要地防空作战过程中，原始的WTA方案往往不能有效应对各种突发状况，因此需要根据实际攻防状态对目标进行DWTA。

自Hosein等在1990年提出DWTA理念以来，引起越来越多的学者兴趣[4]。Ahuja等[5]通过使用网络流公式描述了WTA问题，并提出了下限解法。Kim等[6]开发了一个用于将可用武器重新调度到具有时间相关杀伤概率目标的模型。Karasakal等[7]提出了一种基于射击- 观察- 射击(SLS)交战政策和防御单位之间充分协调的防空分配模型。Davis等[8]为DWTA问题建模了马尔可夫决策过程公式，并提出了近似动态规划方法来解决该问题。Summers等[9]提出了一个DWTA 问题，作为来袭导弹分配拦截器的马尔可夫决策过程。

许多国内学者也就DWTA问题展开了深入研究，Wang等[10]提出了含有多种约束的通用型 DWTA 模型。文献[11]根据对战双方的作战态势，提出了一种DWTA对抗博弈模型。Li等[12]为多阶段WTA问题开发了一种双目标公式，可最大限度地降低失败风险和资源成本。雷鸣等[13]建立了以打击效益最大为优化目标的WTA模型，基于云模型的优良特性，结合遗传算法，提出了一种基于云模型的改进遗传算法。高志华等[14]运用遗传算法建立了WTA模型，使防空武器最大限度地发挥火力单位效能，达到最大毁伤效果。孙海文等[15]将射击有利度、飞临时间与威胁度等因素结合，构建一种新的综合防空WTA模型。

以上国内外学者的研究大多数认为按最初的WTA方案实施作战，便可获得最大的来袭目标拦截效率。然而，在实际海上要地防空作战过程中，原始WTA计划可能会受到原分配目标被消灭、出现新目标以及某一防空武器发生故障等不确定因素的影响，而使得初始方案不可行或拦截效率低下。

本文针对海上要地防空火力再分配问题，提出了一种能够兼顾最大化拦截概率以及最大化武器射击稳定性的双目标优化DWTA模型。其中定义防空武器的射击稳定性为某台防空武器对空中目标持续射击的轮数。通过将目标函数线性化的方法进行双目标函数求解，对3种不确定突发情况进行算例仿真求解，验证了本文提出方法的可行性与有效性。通过与单目标火力规划模型的对比验证了本文算法的优越性，通过大规模样本的算例仿真验证了本文算法的稳定性。

1 不确定因素下防空火力优化模型

1.1 问题描述

假设采用n个武器拦截m个目标，武器和目标之间的交战组由集合V表示，其中(i,j)∈V表示武器系统j与目标i交战，i∈M,j∈N，其中M为来袭目标集合，N为防空武器集合。在确定有效的交战组合时，要综合考虑武器系统的射程、交战区域、拦截概率和火力通道等因素[16-19]。同时假设在开始作战时按照初始WTA方案进行，但在交战过程中原方案可能会被以下3种因素影响。

1)原分配方案中的目标已被摧毁。如果一个武器装备在前几轮的射击中摧毁了分配给它的目标，那么原分配方案中之后用来攻击被摧毁目标的剩余导弹可以用来防御其他目标。

2)武器装备故障。防空武器装备由诸多电子和机械部件构成，这些组件中的一个或多个由于战损、电子干扰、自然环境因素等发生故障，则可能会导致防空武器在交战期间无法使用。

3)交战过程开始后发现新的来袭目标。交战过程中的另一个不确定因素是出现了原WTA预案中没有考虑到的新目标。

1.2 限制条件

当上述突发情况发生时，需求重新进行WTA问题，将重新进行WTA的时间间隙设置为重调度时间点。当前目标和可用武器装备对的集合会在重新调度的时间点更新。

针对本文的研究目的提出以下模型假设：

1)在一个时间点，最多发生一个扰动。

2)如果某武器在交战过程中发生故障，则在交战过程结束之前无法使用。

3)当发现到新的空中目标时，能够检测出新来袭目标的类型、距离、速度和命中概率。

4)各防空武器之间在WTA方面能够充分协调。

1.3 相关定义

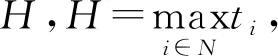
将整个防空作战时间范围划分为相等、不重叠的时间间隙，每次拦截作战从这些时间间隙的起始开始，用k∈K表示，其中k表示每次拦截的时间间隙，K表示整个防空作战时间间隙集[20-22]。假设每次拦截需要恒定的准备时间Δc。防空武器的最大射程和最小射程分别用rmax j和rmin j表示。一个防空武器可以在交战时段[tfij,tlij]内拦截目标，其中tfij是第一次交战的开始时间，tlij是最后一次交战的结束时间。武器j与空中目标i的可交战时间是由防空装备的有效射程和速度以及来袭目标的距离和速度计算得到的。

tfij的计算公式如(1)式所示:

(1)

tlij根据武器最小射程和拦截发生时目标与防御点距离计算：

(2)

作战时间为射击准备时间与敌我目标相遇时间的和，用Δijk表示。飞行时间取决于武器- 目标对的相对速度和交战的开始时隙ρk。如果交战在时间间隙k开始，则交战持续时间Δijk的公式为

(3)

图1显示了时隙、时间范围和时隙的开始时间。来为每个武器- 目标对计算可交战时间段。

图1 防空作战时间线

根据SLS防空作战原则，对每个空中目标进行武器分配。根据SLS原则，在当前交战完成之前，不会对空中目标进行新的WTA。定义集合Tij为武器j和目标i的可调度交战时间段，因为武器j和目标i对之间作战[tfij,tlij]内实现。

Tij={k∈K:(i,j)∈Vand [ρk,ρk+Δijk]⊆[tfij,tlij]}

(4)

武器j和目标i之间的最大交战次数由fij表示，并根据SLS原则通过除以可交战时段计算得出。为了确保根据SLS原则安排交战，为每个目标i和时隙k定义特定集，

Lik={(j,τ):(i,j)∈V,τ∈Tijand [ρk,ρk+Δ]⊆[ρτ,ρτ+Δijτ]}

(5)

如(5)式所示，若目标i和武器j之间的交战在时隙k之前的时隙开始，并在时隙k结束时间之后结束，则(j,τ)对在集合Lik中。

当交战在时隙k的开头开始时，武器j对目标i的单发杀伤概率用pijk表示，并且每个防空武器在重新分配时间点都有可用的次数uj。

构建下列函数以描述整个防空作战过程：

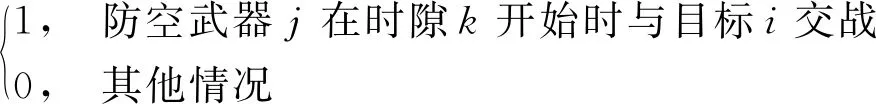
(6)

(7)

定义射击稳定性为连续分配给同一武器的目标总数。图2描述了一个防空武器两个不同射击方案的示例，箭头显示了交战范围内分配的来袭目标编号。图2(a)中，防空武器在交战过程中对同一个空中目标i2进行射击，并且由于不改变目标而具有更好的射击稳定性。图2(b)中，武器必须在每次射击后改变其目标，首先对空中目标2射击，然后对空中目标1射击，最后对空中目标3射击，因此具有较低的射击稳定性。

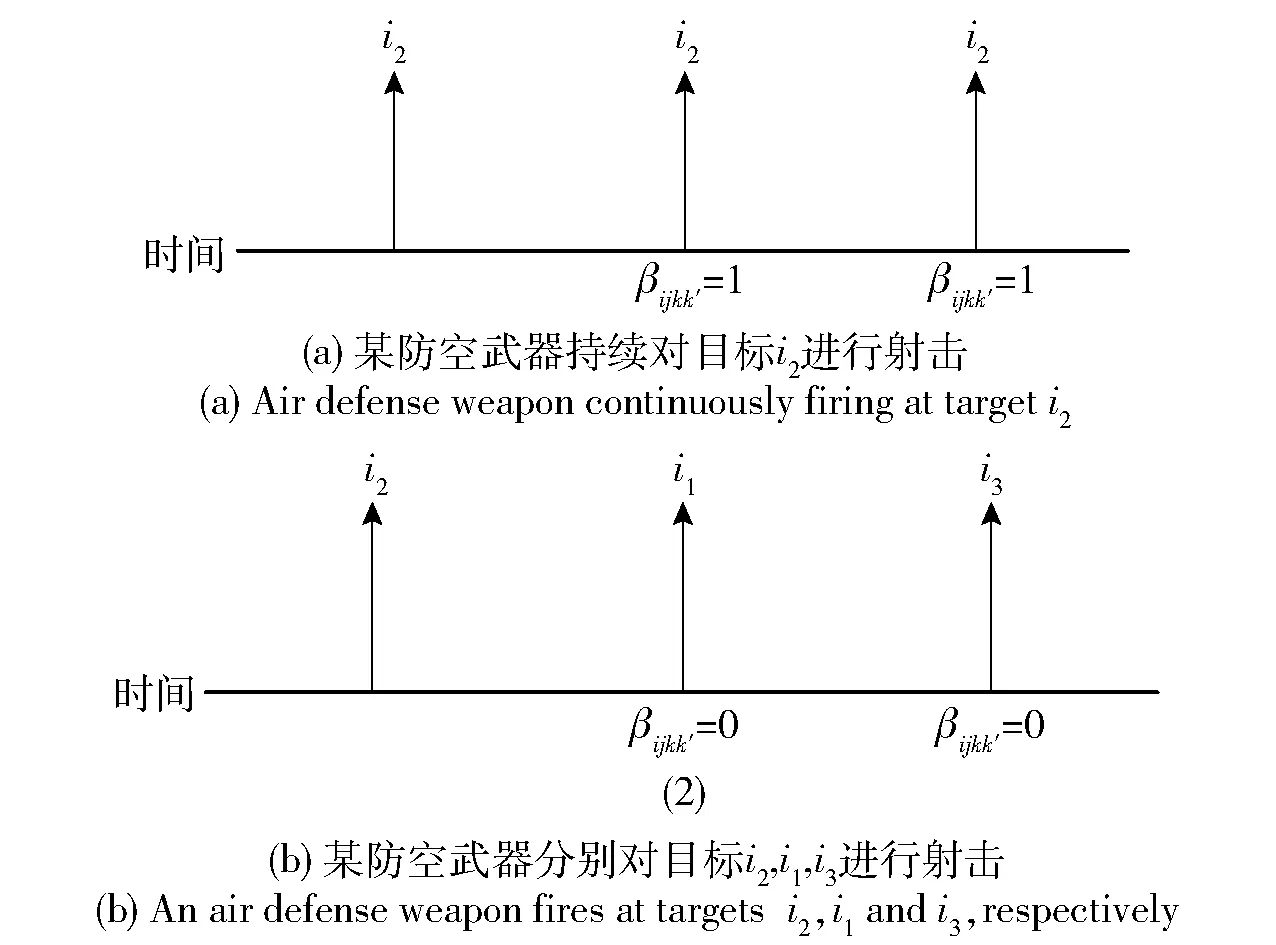
图2 防空武器的两种不同目标分配方案

1.4 WTA优化目标函数

DWTA方案优化目标函数如下：

(8)

(9)

式中：Rj为每型武器最大射击轮数。

(10)

(11)

式中：fij为目标交战次数。

(12)

目标函数即拦截概率最大化SC即最大化来袭目标拦截概率；稳定性目标函数WD即最大限度地将相同的空中目标分配到一个武器的作战安排中。防空武器射击次数由(9)式约束，对于每个武器系统j，分配给空中目标i的轮数必须小于或等于可用轮数。

约束条件(10)式表示武器射击方案必须符合SLS原则。根据集合(j,τ)∈Lik对所有Xijτ变量求和，可确保从不同武器到空中目标的射击不会发生时间重叠。约束条件(11)式明确了可以针对每个目标安排的最大武器轮数。假设根据SLS原则，在可交战时限内，武器系统j可以分配给空中目标i的轮数为2，则约束条件(12)式强制规定，武器系统j最多可以调度2轮对空目标i进行射击。

2 考虑射击稳定性的WTA步骤

本节提出一种考虑防空武器射击目标交换的WTA优化算法。通过在每一步中定义拦截概率的上界来生成最大拦截率与最小拦截率之间的可行解，最后求得各拦截率对应的最佳射击稳定性的目标函数值[23-25]。

2.1 效率目标函数的线性化

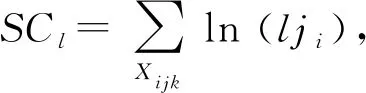
(13)

(14)

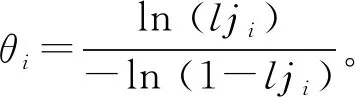
(15)

(16)

(17)

0≤γi1≤C1,∀i∈M

(18)

0≤γip≤Cp-Cp-1,∀i∈M,p=2,3,…,l

(19)

和(9)式～(12)式。

2.2 生成具有不同拦截概率的所有解决方案

为解决双目标WTA问题，首先计算在不考虑稳定性目标函数的情况下生成具有不同拦截效率值的所有解。为了获得具有不同拦截概率的方案，通过在每个步骤中向模型添加以下约束来限制SCl，直到生成具有最小效率值的拦截方案。

(20)

在约束条件(20)式中，将目标函数值限制为具有不同拦截概率的目标函数解决方案，SCmax l值是拦截概率的上限。在第一步中SCmax l设置为1，这是拦截概率可以取的最大值。然后，在每个步骤中通过等于先前找到的拦截概率值来更新SCmax l。通过在每一步中更新在约束条件(20)式的右侧，得到一个新的解决方案，该解决方案的拦截概率比之前找到的要小。继续迭代，直到生成具有最小拦截概率的WTA方案，本阶段不考虑武器系统的射击顺序。

2.3 确定不同拦截率WTA方案稳定性值

本节关注生成的WTA方案的射击目标更改总数，提出一种武器- 目标交换算法，以找到具有不同拦截概率的每个解决方案的最大WD值。交换算法主要包括两种交换情况。

1)每个目标交换分配的武器组合。在目标的WTA方案表中选择一对武器组合，并尝试交换其顺序。搜索是否存在可用的时间段来分配两种武器。如果可以进行交换，将保留新射击方案作为备选WTA方案，然后为每个目标生成所有交换武器的组合。例如，目标的初始WTA方案如图3(a)所示，y轴代表时间范围，矩形表示防空武器。根据SLS原则，在防空武器拦截目标期间，在同一时间段内不得为目标安排其他武器，因此矩形之间没有重叠。矩形的起点和终点显示了交战的起点和终点时间段。矩形的长度代表每次作战的持续时间。在交换算法的第一阶段，交换武器2和武器1的射击命令，并为目标1生成新的时间表。图3(b)显示了更新后的时间表，新方案对于目标1具有相同的拦截概率。

图3 武器- 目标分配方案

2)在两个目标的WTA方案间交换防空武器，保持相同的拦截概率，以在每个可行解决方案中找到最大WD。如果两个不同的武器对两个目标具有相同的单发杀伤概率值，则这些防空武器设计次序可以在两个目标的WTA方案之间交换，并且整个防空的拦截概率值不会改变。对于每对目标，检查不同武器是否具有相同的单发击杀概率值。如果可以在目标之间交换分配的武器，则将更新当前WTA方案。

交换算法通过更新武器系统的射击顺序，来找到WD值最大且不改变拦截概率的WTA方案，最后一个步骤是去除之前产生的不可行WTA方案。在寻找最大WD值的过程中可能会出现一个武器在一个时间段内射击两次的情况。若出现此类情况，则必须将其从可行的分配方案集中删除。计算可行解集中所有解的WD值，并选择WD值最大的解作为备选方案。

对于每对目标，需要检查不同防空武器是否存在相同的单发击杀概率值。若相同，则交换对原目标射击的武器，找到所有可能的武器分配方案。例如，假设目标1-武器1、目标1-武器2、目标2-武器1和目标2-武器2之间的单发杀伤概率相等。图4(a)显示了对目标1的初始WTA方案。若交换第二段武器1和武器2射击目标，则整体的拦截效率不会发生变化，因为单发命中概率值相同。另一方面，武器1和武器2的交战时间表的稳定性可以增加。这可以在相同的效率下产生最大的稳定性值。图4(b)显示了更新后的分配计划。

图4 单发拦截概率相同时可交换对两个目标射击的防空武器

图5表示一个简单的求WTA方案非支配解的求解过程。首先，在不考虑射击稳定性的条件下，通过求解线性化模型得到具有最大效率目标函数值的解AS1。其次，通过武器- 目标交换算法在保持相同拦截效率值的同时最大化射击稳定性，并生成解AS2。最后，使用拦截效率值的界限对模型进行求解，以获得具有不同拦截效率的解，生成解AS3。为了生成此特定拦截效率值的最佳稳定性值，再次应用武器- 目标交换算法并生成解AS4。结果生成了两个解AS2和AS4。重复进行上述步骤，直到获得最低拦截效率的解。

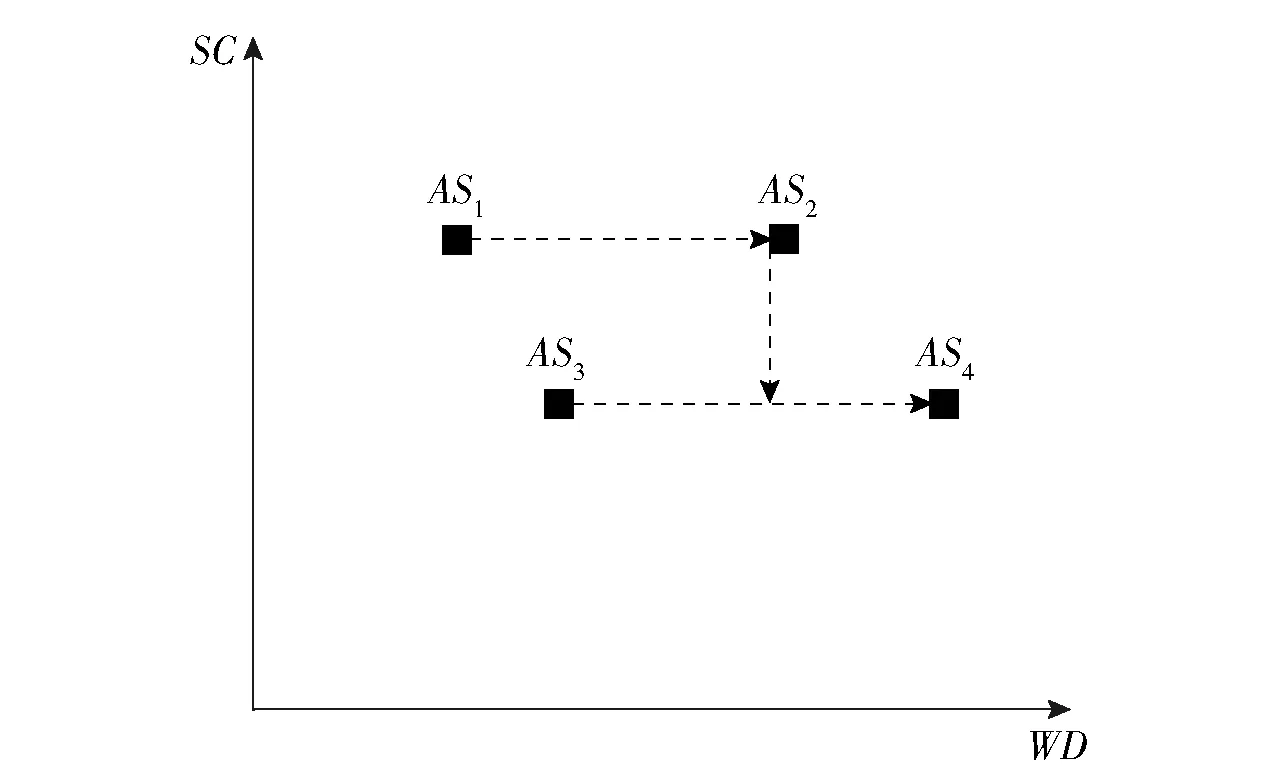
图5 一个WTA方案的生成过程

具体算法步骤如下：

步骤1设置SC=1和WDcur=0。

步骤2进行双目标武器再分配，寻找满足SC、WD的武器分配方案。如果不可行，则停止。

步骤3可行设置解cs并将SCcur设置为拦截概率值，计算WD。

步骤4对于当前的方案cs，Ui更改集合Ui中为每个目标i分配的武器顺序。找到所有可能的武器序列，并为每个目标i添加设置XLi，XLi为目标i分配的所有可能的武器序列集。

步骤5从集合Ui中为每个目标 选择一个分配计划，并找到防御的交战分配计划的所有组合并添加到集合JZ(防御交战分配方案集)。

步骤6判断集合JZ中的解是否包括武器系统在同一时间段内多次射击，从集合JZ中删除这些不可行的解决方案。

步骤7对于每个目标对，检查是否有机会用相同的单发命中概率对交换分配的武器。如果可以进行交换，则更新当前计划cs。转步骤2。

步骤8为集合Ui中的每个解决方案计算WD。

步骤9从集合Ui中选择具有最大WD的解λ。

步骤10如果WDλ则将解WDcur添加到 并设置WDλ=WDcur。将约束SCλ≤SCcur-ε添加到双目标火力分配方案，转步骤1。

算法实现逻辑图如图6所示。

图6 算法步骤示意图

3 算例仿真

表1为防空武器和来袭目标性能参数。根据海上要地防空作战的实际情况，从表1的三型防空武器装备中选取防空武器，对四型空中目标进行防空作战仿真，验证本文提出的WTA算法。各武器装备的参数，参照各种文献资料中已经公开的参数进行计算。从每型武器系统中分别选出2台和3台武器系统，各自构成2×2×2与3×3×3的防空线。仿真环境为CPU:i7-8850H，16.0GB RAM，操作系统Windows10，仿真实验工具MATLABR2018a。

表1 防空武器系统和空袭目标参数

从表1中随机选择一个空中目标，并随机选择这个空中目标要摧毁的防御单位。重复此步骤，直到选择够m个空中目标为止。据此建立武器与目标(i,j)∈V的有效交战组合矩阵。随机设定当前空中目标距离为60～80 km，每个情况中的武器- 目标对都是在表中随机选择的。

规定时隙的持续时间为1 s，从[0.50，0.80]概率区间内的均匀分布为目标和防空武器创建了一个单次射击命中概率矩阵样本。每次射击的准备时间为9 s，每次可行拦截所花费的时间由恒定的准备时间和目标相遇时间之和计算。

在进行算例仿真时，首先根据最大拦截概率建立最优初始调度进行防御；然后通过仿真程序模拟1.1节中考虑的以下3种突发情况：

1)根据均匀分布生成一个随机数，当随机数值小于单发命中概率时，则武器- 目标对的交战结果是击毁目标。

2)针对武器系统故障的情况，假定其中一台武器装备在交战过程开始后无法发射，武器的破损和破损时间随机确定。

3)当有新的来袭目标时，假设雷达发现一个突然的来袭目标后，交战过程开始，初始计划生效。泊松分布随机确定到达点，新目标的距离和速度是随机确定的，得到新目标与防空武器之间的有效组合、交战的可用时隙和最大交战次数。

本文定义的相关属性参数符号及含义如表2所示。来袭目标和防空武器从表1中随机选取，仿真计算得到不同情况下较优非支配解的仿真结果如表3所示。

表2 部分本文定义的属性符号及含义

表3中，当武器系统数量为9、来袭目标数量为3时多次算例仿真的结果一致，即SC=1,WD=9，因此在表2中只对这一组结果进行记录。为更好地评估WTA方案的拦截效率和稳定性，本文定义了不同的度量标准，并对结果进行了分析。具体度量的量及含义如表4所示。计算结果见表5。由表5可见：当目标数为6、武器系统数为6时，平均MIE和APIE值最高；当目标数为3、武器系统数为9时，平均MIE和APIE值最低。

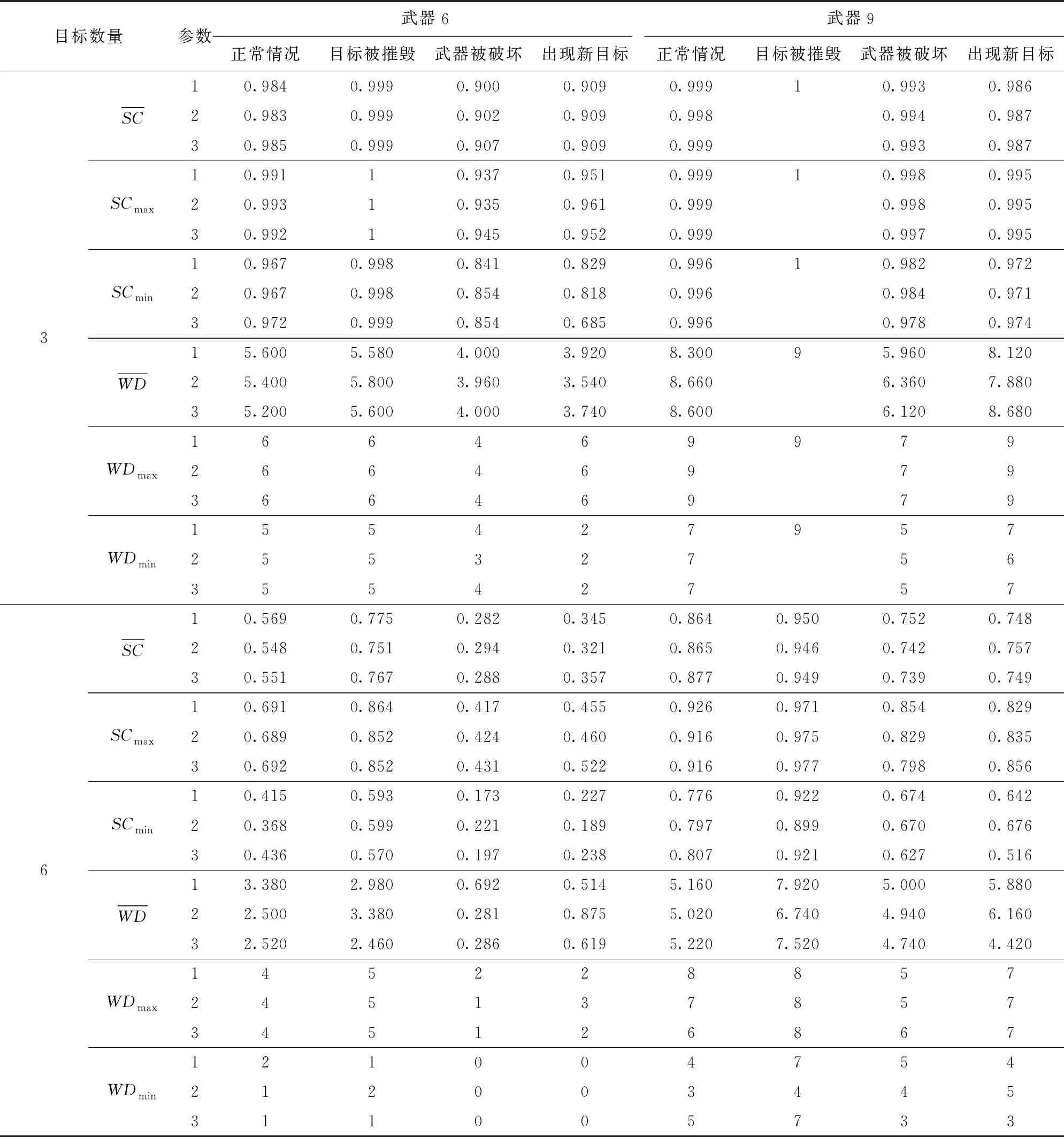
表3 各情况下的较优非支配解

表4 本文定义的度量的量及含义

表5 不同情况下数据处理结果

在目标被提前消灭的情况下，MIE均值在0～0.285之间。在6个目标-6个武器系统和3个目标-9个武器系统的情况中，MIE的最大值分别为0.282和0.076。结果表明：目标数量增加或武器系统数量减少，平均MIE和APIE结果增加；在6个目标-6个武器系统，MTC的最大平均值为3.667。在3个目标-9个武器系统的情况中MTC的平均值最低，为0。结果表明，平均MTC随着目标数量的增加而增加，随着武器系统数量的增加而减少。在6个目标-6个武器系统的情况中，获得了最大APIEC值，达到3.367%，因此可以说一次目标转换对该情况下的拦截效率提高了3.367%。当3个目标-9个武器系统时不需要进行射击次序交换即可完成拦截任务，因此APIEC值无实际意义。

在武器故障情况下，当6个武器系统的情况中目标数从3个增加到6个时，MIE平均值从0.089增加到0.227。此外，在这些问题集中，MPIE平均值从3.947%增加到47.301%。在6个目标-6个武器系统的情况下，获得了最高的MIE、MPIE和APIEC平均值。在3个目标-6个武器系统的情况中，获得了最低的平均MIE、MPIE和APIEC值。平均MTC值随着武器系统和目标数量的增加而增加。在6个目标-6个武器系统的情况中，最大平均MTC值分别为1.333。在6个目标-6个武器系统的情况中，最大MPIE值达到49.705%。因此，在该情况下几乎实现了50%的拦截效率改进增量。

在新目标情况下，在6个目标-6个武器系统的情况中，最高的平均MIE值为0.261；在6个目标-9个武器系统的情况下，它减少到0.228。在6个目标-6个武器系统的情况中，MPIE的平均最高值为40.493%。因此，系统的拦截效率在这种情况下提高了50%。在3个目标-9个武器系统的情况下，MPIE平均值最低的是0.821%。

结果表明，在各种突发情况下，当武器系统数量有限和来袭目标多的情况下，重调度方法的效果更为显著。当武器系统数量增加或空中目标数量减少时，效率的提高就会降低。MTC值随着武器系统或目标数量的增加而增加。

表6显示了各情况下的仿真运行时间。运行时间取决于武器与目标的有效交战次数、各武器系统中武器弹药的数量。当问题变得复杂时，运行时间就会增加，这与现实情况基本一致。由于海上要地防空作战WTA属于在战前进行，算法仿真运行时间基本可以满足要求。

为了验证本文提出算法的优越性，采用尽考虑来袭目标拦截概率的单目标优化算法，在相同仿真环境、相同仿真条件下进行DWAT仿真计算，具体仿真结果如表7所示。

表6 不同情况下求解的耗时

表7 仅考虑来袭目标拦截概率的单目标优化算法仿真结果

由表6可知，仅考虑来袭目标拦截概率的单目标DWTA算法较本文提出的算法目标拦截概率较高。但单目标算法给出的WTA方案武器射击稳定性过低，在实际防空作战时由于不同武器系统之间的反复调度很可能会延误宝贵的作战时机、浪费有限的作战资源，不能很好地满足海上要地防空作战对WTA方案时效性的要求。

为测试本文方法的稳定性，在相同仿真环境下，扩大实验规模分别采用来袭目标数9-防空武器数6；来袭目标数12-防空武器数9为初始条件，验证本文提出的WTA算法。具体仿真结果见表8。由表8可见，本文提出的模型在来袭目标数量较大的情况下，依然能够收敛，给出目标拦截概率及武器系统射击稳定性。

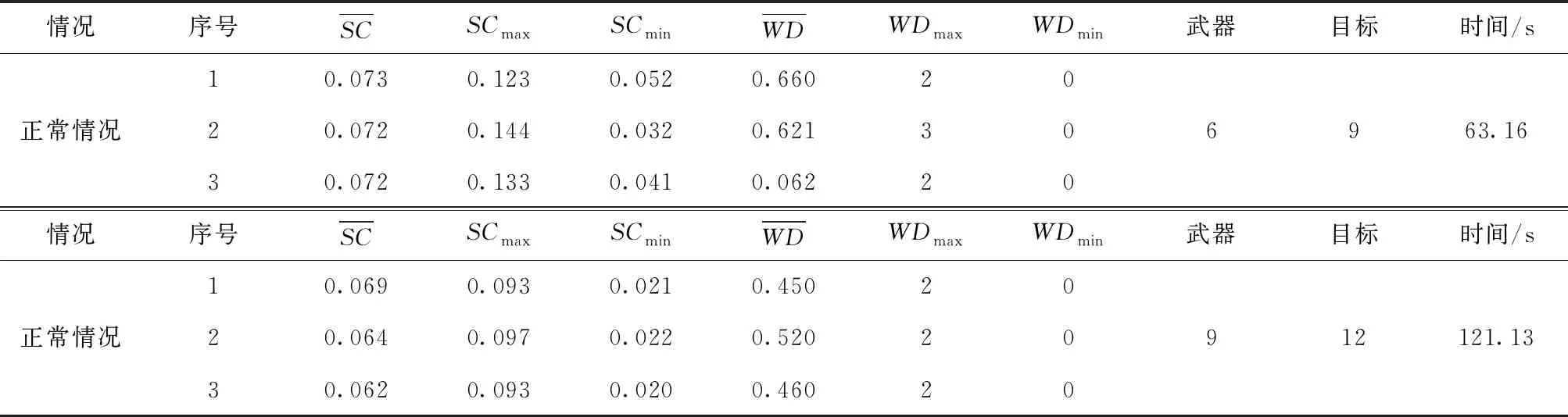
表8 扩大实验规模后的仿真结果

4 结论

本文提出了一种考虑不确定因素的新的防空武器DWTA模型。将原分配目标被击毁、防空武器故障和发现新目标3种情况作为当前分配方案的不确定扰动。建立了一种双目标模型，将拦截概率作为效率测度，将对同一目标连续射击的总次数作为稳定性测度。同时为求解双目标数学模型，提出了一种新的求解方法。由于WTA问题是一个非线性整数规划问题，首先对效率目标函数采用了线性化方法，然后在不考虑防空武器射击稳定性的条件下，生成了具有不同拦截概率的可行解；最后利用这些可行解，在防空武器分配方案中通过交换射击目标次序生成非支配解。结果表明，本文提出的方法可用于解决不确定因素下的动态火力规划问题，并能辅助指挥员进行防御决策制定。