分段压裂诱导地热储层应力场响应的单连通解析模型分析

王 伟，陈劭颖，杨清纯，刘和平，张立松

（1.中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580；2.中国建筑标准设计研究院有限公司，北京 100037）

目前，地热储层水力压裂多采用分段压裂技术[1]，该技术可以有效提高地热储层的渗流能力[2]。然而，该技术引发的力学问题同样值得关注[3]，特别是分段压裂诱导的地热储层应力场响应问题，尚未见到相关报道。考虑到地热储层压裂为热流固耦合问题[4]，分段压裂诱导地热储层应力场响应的本质为热流固耦合作用下缝间应力干扰问题[5]。由于储层应力场响应的载荷特性，将对地热储层井筒完整性和套管变形产生直接影响[6]，因此，开展分段压裂诱导地热储层应力场响应研究具有重要意义。

目前，国内外学者关于储层应力场响应开展了大量工作，国内学者邵尚奇等[7]运用势理论建立了无限大地层Ⅰ-Ⅱ复合型裂缝周围应力场解析模型，得到地应力和流体压力双重作用下Ⅰ-Ⅱ复合型裂缝应力场函数和复合裂缝应力场解析表达式。王宇等[8]从岩石的细观非均质特性出发，采用岩石破裂失稳的渗流-应力-损伤耦合分析系统，设计了一系列的数值试验揭示水力裂缝间的应力阴影效应。刘文政等[9]通过对比考虑温度场与不考虑温度场的数值结果，得出了在压裂过程中基质应力场、裂缝内流场和地层温度场三场间存在很强的相互作用的结论。马许平等[10]利用ABAQUS软件建立了二维流固耦合水力压裂数值模型，并利用扩展有限法模拟了单射孔压裂、两射孔异步压裂、两射孔同步压裂这3种工况下水力裂缝之间的干扰问题。张建国等[11]建立了考虑压裂液流动与岩体变形耦合作用机制的段内多簇同步扩展有限元分析模型，据此模型得出多裂缝同步扩展过程中会产生附加应力场且裂缝形态会受到影响的结论。另外，孙可明等[12]、刘立峰等[13]、邓燕等[14]也对储层应力场响应进行了深入研究。国外学者KIM等[15]建立了热流固三场耦合的裂缝扩展模型，基于此模型讨论了储层应力场变化。PALMER[16]分析了多裂缝间的应力干扰问题，得出了缝间应力干扰会诱使裂缝附近应力发生偏转进而影响后续裂缝扩展的结论。ROUSSEL等[17]运用由一个或多个支撑裂缝产生的应力干扰三维数值模型，计算了压裂条件下诱导应力产生的应力转向程度。HOSSEINI等[18]研究了不均匀裂缝扩展背后的物理机制，结果表明裂缝间的缝间干扰现象会抑制裂缝的正常扩展，而通过控制段内裂缝簇数、裂缝簇间距等因素可以减弱这种缝间干扰作用。KRESSE等[19]基于增强的平面非常规裂缝模型，给出一种计算复杂水力裂缝网络中应力阴影的方法，利用该方法可以近似计算出复杂裂缝网络中不同裂缝分支之间的相互作用。PEIRCE等[20]建立了一个全新的三维水力裂缝模型，研究了考虑缝间干扰的裂缝扩展，结果表明当射孔簇均匀布置时，应力阴影会使裂缝延伸主要集中于外侧裂缝，而当射孔簇不均匀布置时，裂缝的延伸更加均匀。

综述前人进展，已取得了丰富成果，但并未给出分段压裂诱导地热储层应力场响应的计算方法。现阶段普遍采用线弹性断裂力学求解缝间应力干扰问题，然而该方法并不能求解分段压裂诱导地热储层应力场响应，即不能计算热流固耦合作用下缝间应力干扰问题。

鉴于此，从方法创新的角度出发，引入连续性假设将断裂力学问题转化为弹性力学问题，建立分段压裂诱导地热储层应力场响应的单连通解析模型，以降低求解难度；同时，基于ABAQUS建立地热储层分段压裂热流固耦合数值模型，通过对比x、y方向平均应力验证解析模型的准确性；最后，利用解析模型讨论簇数、温差和天然裂缝对地热储层应力场的影响（图1）。

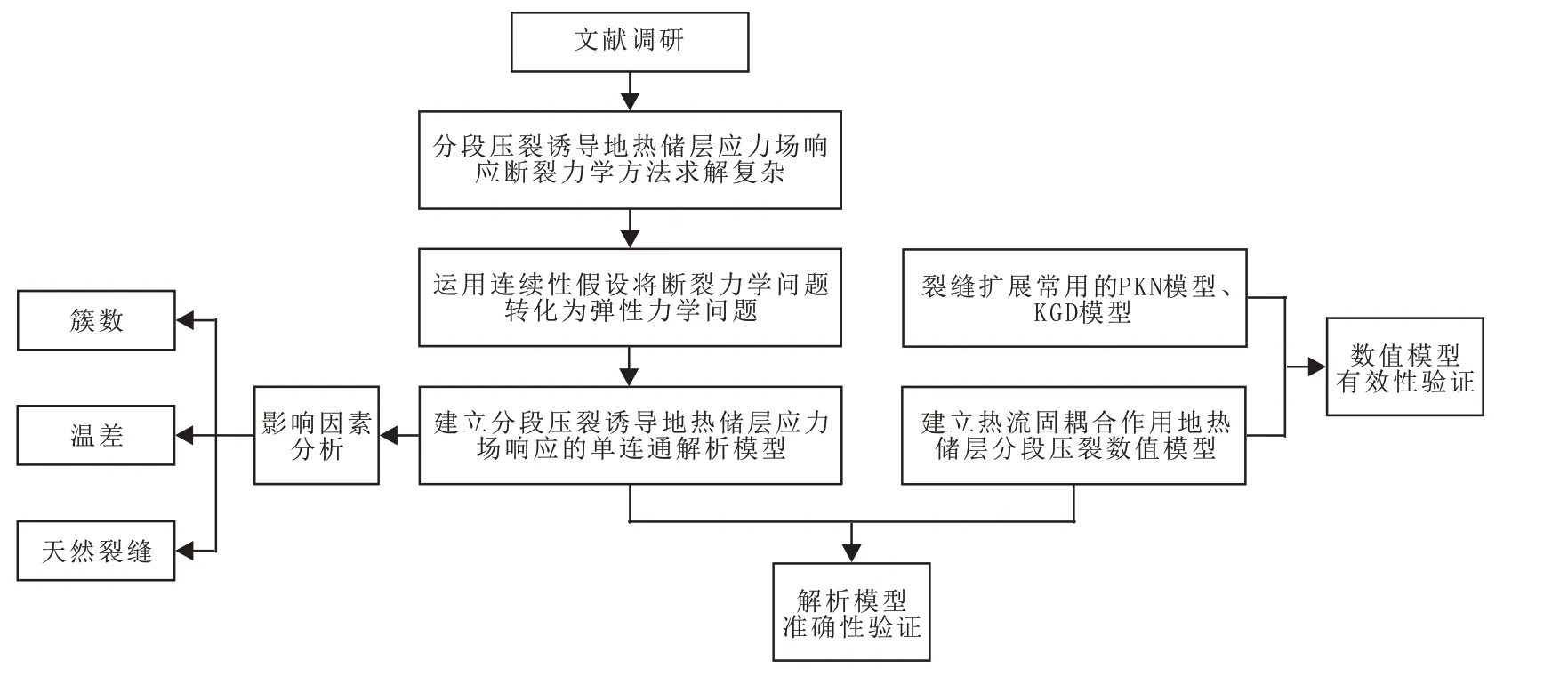
图1 技术路线Fig.1 Technology roadmap

1 地热储层诱导应力场单连通解析模型

1.1 物理模型

目前，普遍采用断裂力学对水力压裂诱导的应力场响应进行求解[21]，然而，分段压裂诱导地热储层应力场响应的本质为热流固耦合作用下缝间应力干扰问题，这使得利用断裂力学方法求解应力场响应的难度极大[22]。鉴于此，基于裂缝宽度远小于储层尺寸这一条件及力学中的连续性假设，将这一复杂的断裂力学问题转化为弹性力学单连通问题（图2）。

如图2所示，将裂缝宽度转化为等效位移载荷，进而将断裂力学模型转化为弹性力学单连通模型。

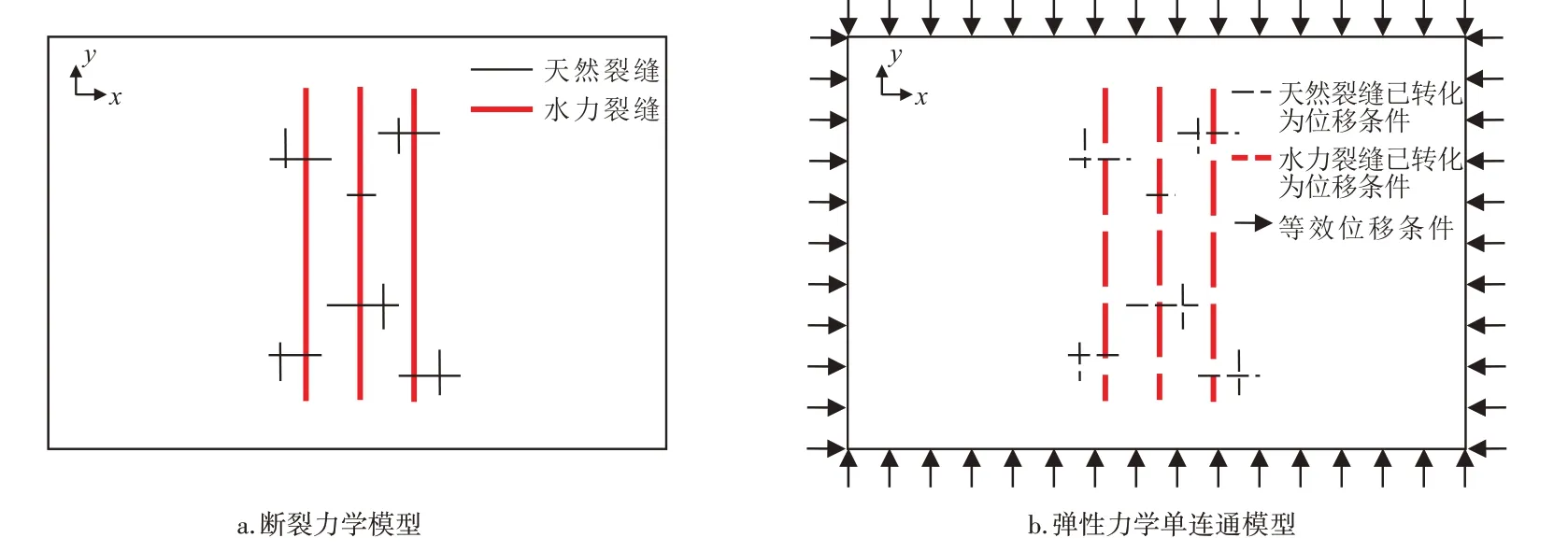
图2 断裂力学模型转化为弹性力学单连通模型示意图Fig.2 Transformation of fracturing mechanics model to simply connected model in elastic mechanics

1.2 力学模型

设压裂引起的地热储层x方向应力分量为σ＇x，则根据应变表示应力物理方程有：

式中：σ＇x为压裂引起的地热储层x方向应力分量，MPa；θ为体应变；εx为压裂引起的地热储层x方向应变分量；λ和G为拉梅常数，MPa。

λ和G可由下式表示：

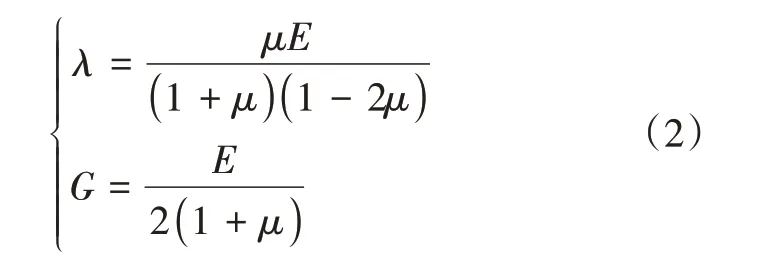
式中：E为杨氏模量，GPa；μ为泊松比。

体应变θ在数值上等于应变张量的第一不变量，即θ=εx+εy，则式（1）可表示为：

式中：εy为压裂引起的地热储层y方向应变分量。

应力表示应变物理方程为式（4）及式（5）：

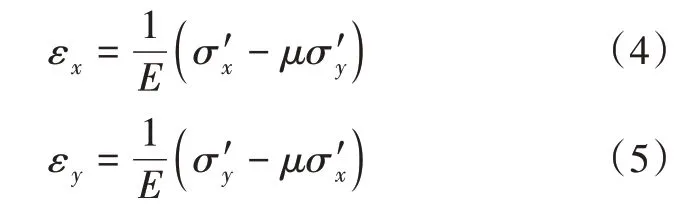
联立式（4）及式（5）求解可将εy由σ＇x和εx表示，如式（6）所示：

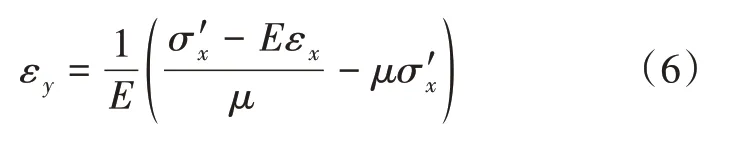
将式（2）及式（6）代入式（3）简化后得：

则考虑热应力条件下压裂引起的地热储层x方向应力分量σx为：

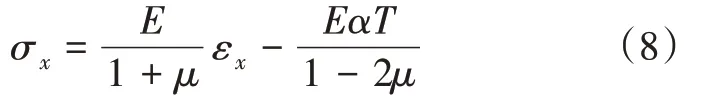
式中：α为线膨胀系数，℃-1；T为温度变化，℃，压裂过程中地热储层温度变化为负值。

利用几何方程εx=，式（8）可进一步表示为：

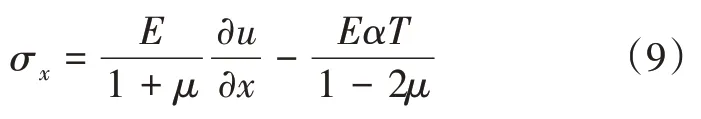
式中：u为x方向位移分量，m；可由下式求得：

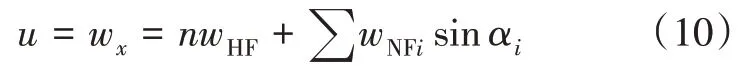
式中：wx为x方向总裂缝宽度，m；n为压裂簇数；wHF单簇水力裂缝宽度，m；wHFi为第i条天然裂缝宽度，m；αi为第i条天然裂缝与水平方向夹角，°。

式（9）表明压裂引起的地热储层x方向应力分量σx可由x方向等效位移载荷（即x方向裂缝宽度）与温度变化表示，且与x方向等效位移载荷成正比、与温度变化成反比。

设压裂引起的地热储层y方向应力分量为σ＇y，则根据应变表示应力物理方程有：

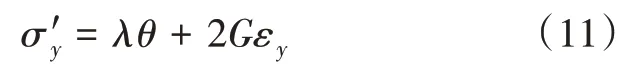
式中：σ＇y为压裂引起的地热储层y方向应力分量，MPa。

利用体应变θ=εx+εy可将式（11）表示为：

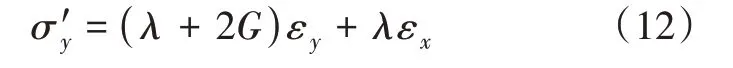
联立式（4）及式（5）求解可将εy由σ＇y和εx表示，如式（13）所示：

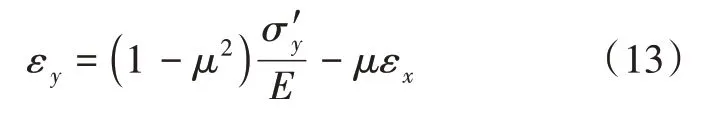
将式（2）及式（13）代入式（12）简化后得：

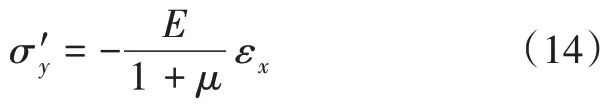
则考虑热应力条件下压裂引起的地热储层y方向应力分量σy为：

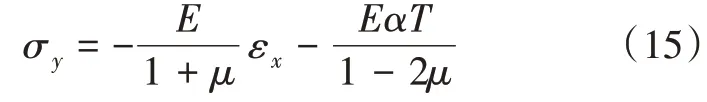
利用几何方程εx=，式（15）可进一步表示为：

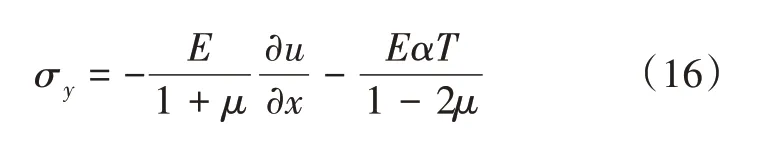
式（16）表明压裂引起的地热储层y方向应力分量σy可由x方向等效位移载荷（即x方向裂缝宽度）与温度变化表示，且与x方向等效位移载荷、温度变化均成反比。

利用此解析模型可以对现场压裂后的应力场响应进行分析，即通过微地震等技术手段监测现场压裂裂缝宽度，进而将监测到的裂缝宽度转化为相应的位移载荷，最后运用解析模型获取现场压裂后的储层应力场响应。

2 解析模型的数值验证

为验证所建解析模型的准确性，基于ABAQUS建立热流固耦合作用下地热储层分段压裂数值模型，对解析模型进行数值验证。

2.1 有限元模型建立

1）几何模型。所建模型尺寸为120 m×80 m，并在模型中预制裂缝的扩展路径及天然裂缝分布，如图3a所示。

2）网格划分。储层部分采用支持渗流的CPE4P四面体单元，水力裂缝部分采用Cohesive单元组成，天然裂缝以及射孔部分采用初始损伤单元组成，并在裂缝附近对网格进行加密以提高计算精度。同时，为了实现天然裂缝与水力裂缝的沟通，在网格中对渗流节点进行了合并，这样可以使水力裂缝中的流体进入天然裂缝并实现天然裂缝的扩展。

3）边界条件。由于储层一般被认为是无限大地层，因此在模型边界位移上采用固定约束边界条件，在模型注入点采用定流量方式施加流体压力载荷，在边界压力条件上采用0孔隙压力边界，通过施加预定义场设置储层的原位地应力及温度。

另外，模拟所采用的基本参数如表1所示。

表1 基本参数Table 1 Basic parameters

如图3b所示，在裂缝尖端位置x方向应力会产生应力集中，同时，裂缝附近的储层由于受到挤压x方向应力也发生较大变化；如图3c所示，由于压裂液的注入，裂缝内及裂缝附近的孔隙压力远高于其他位置处的孔隙压力；如图3d所示，由于压裂液温度较低，裂缝内温度远低于其他位置，且裂缝附近储层的温度也受到压裂液影响发生变化。

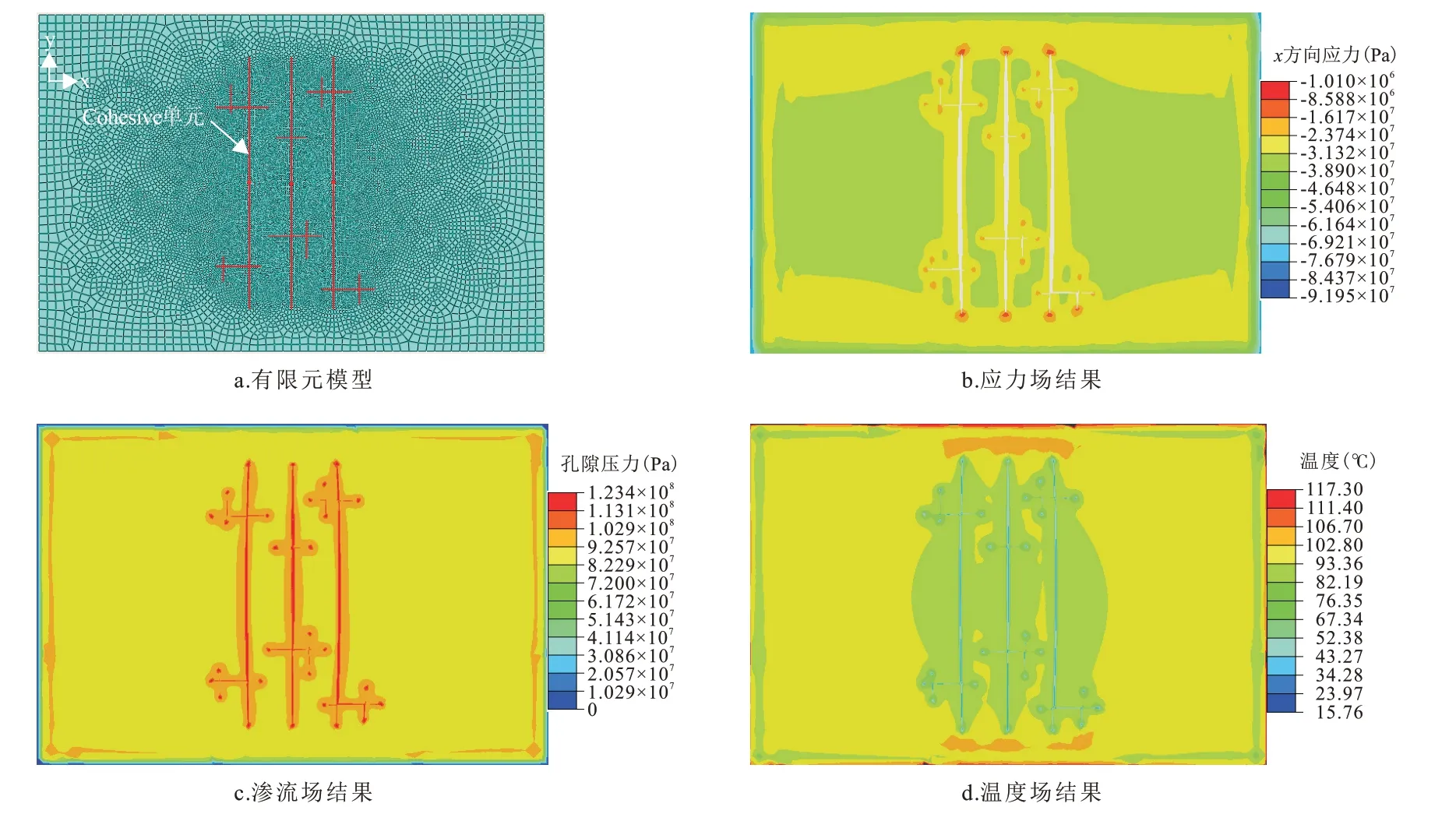
图3 地热储层压裂数值模型Fig.3 Numerical model of geothermal reservoir fracturing

2.2 数值模型有效性验证

为验证所建数值模型的有效性，从裂缝长度、裂缝宽度与裂缝扩展常用的PKN模型、KGD模型的结果进行了对比验证（图4）。

如图4所示，裂缝长度、裂缝宽度与PKN模型、KGD模型的结果误差在5%以内，拟合程度较高，即所建数值模型的有效性得到验证。

图4 数值模型有效性验证Fig.4 Numerical model validation verification

2.3 解析模型准确性验证

为验证解析模型的准确性，通过数值模型获取地热储层内x、y方向应力分量σx、σy平均值及x方向裂缝宽度，并与解析模型所求地热储层内x、y方向应力分量σx、σy进行对比，验证上述解析模型的准确性（图5）。

随着压裂的进行，由于裂缝扩展主要是以扩展方向为x方向的水力裂缝为主，而裂缝扩展会对储层形成挤压作用，导致地热储层内x方向应力分量σx平均值均随之增大，y方向应力分量σy平均值均随之减小，如图5所示，解析模型和数值模型结果均符合此变化规律。且从图5中可知，压裂完成后地热储层内x、y方向应力分量σx、σy平均值数值解与解析解之间相差小于5%，进一步验证了解析模型的准确性。

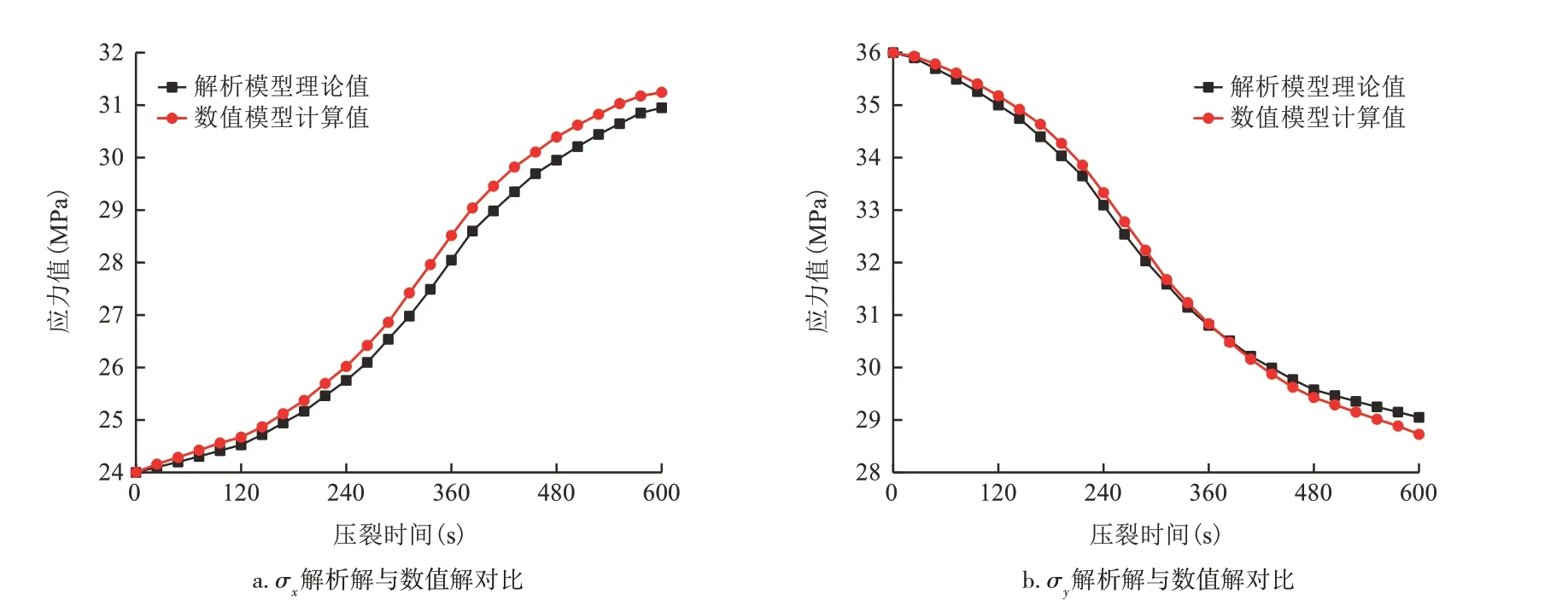
图5 解析解与数值解对比Fig.5 Analytical solution versus numerical solution

3 影响因素分析

3.1 簇数的影响

图6a对比了不同簇数条件下的地热储层内x方向应力分量σx，图6b对比了不同簇数条件下的地热储层内y方向应力分量σy。

随簇数增加，水力裂缝扩展更加简单，导致x方向裂缝宽度随之增大，则由解析模型可知地热储层内x方向应力分量σx随簇数增加而增大（图6a）；另外，由解析模型可知地热储层内y方向应力分量σy随簇数增加而减小（图6b）。

图6 簇数对地热储层应力场的影响Fig.6 Influence of cluster number on stress field of geothermal reservoir

3.2 温差的影响

温度变化由压裂液和储层温差决定，因此，分别对比了不同温差条件下的地热储层内x、y方向的应力分量σx、σy（图7）。

由于储层温度变化为负值，因此，储层温度变化随压裂液和储层温差增大而减小，则由解析模型可知地热储层内x方向应力分量σx随压裂液和储层温差增大而增大（图7a）；另外，由解析模型可知地热储层内y方向应力分量σy随压裂液和储层温差增大而增大（图7b）。

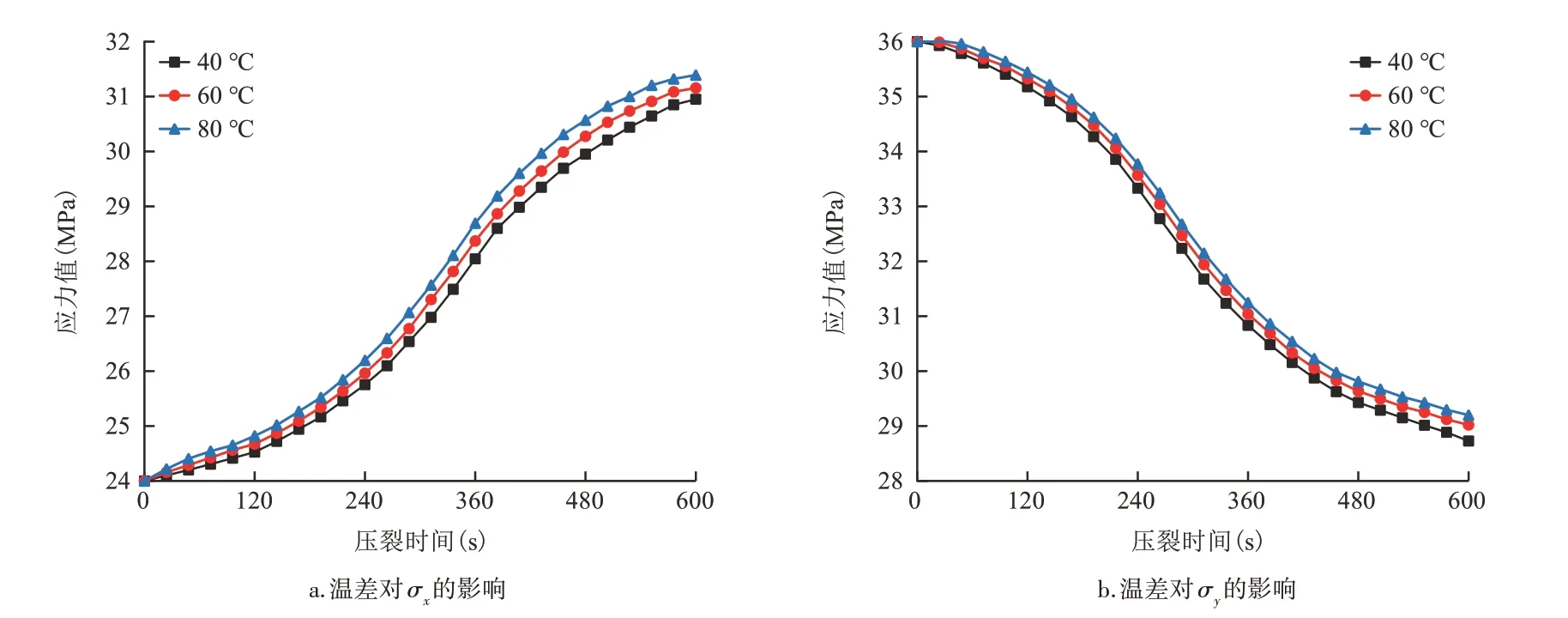
图7 温差对地热储层应力场的影响Fig.7 Influence of temperature difference on stress field of geothermal reservoir

3.3 天然裂缝的影响

通过分别对比不同天然裂缝条件下的地热储层内x、y方向的应力分量σx、σy（图8）可知，随着天然裂缝的密集程度增加，地热储层内x方向应力分量σx随之增大；随着天然裂缝的密集程度增加，地热储层内y方向应力分量σy随之减小。

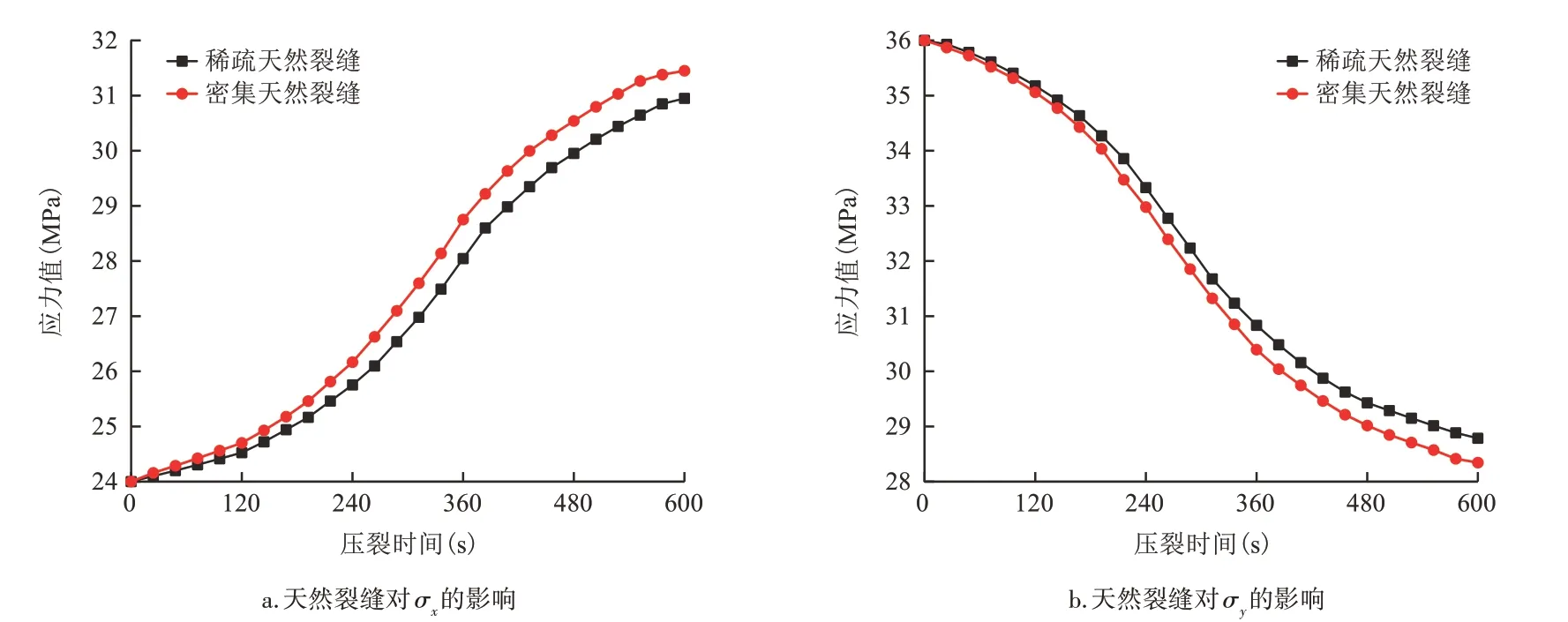
图8 天然裂缝对地热储层应力场的影响Fig.8 Influence of natural fractures on stress field of geothermal reservoir

4 结论

1）基于断裂力学分析分段压裂诱导地热储层应力场响应使求解异常复杂，采用连续性假设将断裂力学问题转化为弹性力学问题，建立了分段压裂诱导地热储层应力场响应的单连通解析模型，利用此模型可简便有效地分析分段压裂诱导的地热储层应力场响应，进而应用到现场压裂中对现场压裂后的应力场响应进行分析。

2）基于有限元分析软件ABAQUS建立地热储层分段压裂热流固耦合数值模型，并与PKN模型、KGD模型对比裂缝长度、裂缝宽度，结果误差在5%以内，验证了所建数值模型的有效性；进而通过对比数值模型和解析模型x、y方向平均应力，结果误差在5%以内，验证了分段压裂诱导地热储层应力场响应的单连通解析模型的准确性。

3）讨论了簇数、温差和天然裂缝对地热储层应力场的影响，结果表明：随着簇数增加，地热储层内x方向应力分量随之增大，y方向应力分量随之减小；随着温差增大，地热储层内x、y方向应力分量均随之增大；随着天然裂缝密集程度增加，地热储层内x方向应力分量随之增大，y方向应力分量随之减小。