具有随机增益的电力系统弹性负荷频率H∞控制
姚方方,张欣雨
(安徽电气工程职业技术学院,合肥 230051)
0 引言
在过去几十年里,负荷频率控制在电力系统负荷波动的情况下,因其能够将系统频率调整到预定值的强大能力,受到了相当大的关注[1-3]。对于传统的负荷频率控制,控制信号/测量值通过专用通信信道传输。众所周知,随着开放式通信网络的应用,现代的负荷频率控制是通过开放的通信网络传输,但在负荷频率控制系统不可避免地会出现常数时延或时变时延等现象。目前,已经报道了许多关于受通信延迟影响的电力系统的负载频率控制的研究成果[4-8]。例如,在文献[4]中研究了考虑到时间延迟(恒定和时变延迟)的具有负荷频率控制的电力系统的稳定性。在李亚普诺夫稳定性理论和积分不等式技术的基础上,提出了一个确保系统稳定性的新标准。在文献[6]中,作者研究了负载频率控制系统在不同类型的时变/恒定延迟下的延迟相关镇定方法。Peng与Zhang等人在文献[8]通过考虑时滞的影响,研究了电力系统的稳定性问题。
一般而言,执行器在控制系统中起着非常重要的作用,因为执行器突如其来的故障会导致整个电力系统性能损坏甚至使得系统变得不稳定。因此设计了可靠的控制,以可靠的方式获得指定的系统性能是十分有必要的。文献[9]采用基于线性矩阵不等式的优化算法,提出了一种针对随机变化的电力系统设计具有混合执行器故障的容错状态反馈控制器的方法。文献[10]通过非脆弱采样数据控制方法解决了具有恒定时延和扰动的不确定多区域电力系统的可靠负荷频率控制设计问题。文献[11]研究了具有执行器故障的马尔可夫跳跃系统的异步基于观察器的滑模控制。此外,文献[12] 为了提高最大功率点跟踪的动态性能和可靠性,本文提出了一种风力发电系统的自适应主动容错控制策略,克服了执行器潜在部分丢失、未知的建模错误和外部干扰问题。
需要注意的是,现有的关于执行器故障补偿方案的结果大多是针对确定性情况提出的[13-20]。如文献[13] 基于高阶滑模微分和离散时间优化技术 研究了具有噪声测量的被动非线性系统的输入估计和补偿问题。文献[15]介绍了在存在未知死区、外部干扰和执行器故障的情况下,一类大规模时间延迟非线性系统的自适应神经补偿方案。在这篇文章中,引入了二次Lyapunov-Krasovskii函数来解决系统的延迟。通过使用径向基函数神经网络来估计系统的未知函数。此外,还开发了一个干扰观测器来逼近外部干扰。所提出的自适应神经补偿控制方法是通过利用反步技术构建的文献[20]讨论了在未建模的系统动力学和无限多的时变执行器故障存在的情况下的柔性操纵器的新型自适应补偿策略。与现有结果不同的是,未建模的系统动力学由非线性时变延迟函数表示,借助于神经网络技术和Lyapunov-Krasovskii函数来解决这个问题。但在现实中,由于环境情况的随机变化,执行器故障也是随机的。与已有的确定性可靠控制结果相比,迄今为止,关于随机性质下控制元件失效的研究文献很少。在这方面,文献[21]研究了一系列复杂动态网络的基于观测器的同步问题,这些网络受到时间延迟、外部干扰、随机发生的执行器故障和输入饱和的影响。文献[22]对非线性挠性航天器进行了随机执行器失效建模,并通过采样数据控制实现了有限时间姿态稳定。此外,随机执行器故障的可靠控制在控制器设计中具有现实意义。因此,我们在本文中考虑随机情况下执行器故障的问题。
另一方面,在动态系统的控制实现过程中,由于环境的影响,控制增益会随机偏离。在这种情况下,需要用随机的方法来考虑增益的变化来容忍偏差。随机发生增益波动的弹性控制的研究在文献[23-30]中得到了关注。例如,在文献[23]中,针对增益随机变化的模糊系统有限时间无源问题,提出了弹性可靠控制。文献[24]讨论了一类具有两种不同类型的忆阻函数和不确定的时变延迟的忆阻神经网络的非脆弱状态估计问题。为了实现混沌Lurie系统的同步准则,文献[25]设计了随机发生控制器增益波动的不易脆裂的控制。文献[27]讨论了一类具有执行器故障的随机系统的基于耗散性的弹性采样数据控制问题。特别是,假设控制器拥有不同故障率的概率性执行器故障。此外,控制器的增益波动以随机的方式出现,服从于某些伯努利分布的白噪声序列。文献[28] 通过使用具有时变概率度量的伯努利分布白色序列来考虑控制器的增益矩阵中的随机波动。 提出了基于无源理论的一类网络化控制系统的弹性控制器设计问题。文献[30]讨论了由区间值模糊模型近似的非线性网络化控制系统的基于耗散性的非脆弱可靠性采样数据异步合成问题,该系统具有随机发生的参数不确定性和控制器增益波动同时对抗半马尔科夫型混合执行器故障。
基于李雅普诺夫稳定性理论和线性矩阵不等式方法,在各种负荷频率控制技术下,电力系统模型的稳定性和镇定问题得到了广泛的研究。例如,文献[31]通过比例、积分和微分型负荷频率控制方案研究了电力系统的时滞相关鲁棒稳定性。同样,文献[32]和文献[33]中分别采用自适应事件触发负荷频率控制和弹性事件触发负荷频率控制技术分析了电力系统的稳定性问题。然而在弹性可靠H∞负荷频率控制设计下,没有考虑具有随机增益波动和执行器故障的电力系统的稳定性和镇定性,这是本文的主要研究动机。
受上述讨论的启发,本文的主要工作是研究弹性可靠H∞负荷频率控制下电力系统的稳定性和镇定准则。本文的主要贡献如下。
1)与已有文献不同的是,本文提出的电力系统模型容易受到外部负荷扰动、随机执行器故障和随机发生增益波动的影响。
2)推导了随机执行器故障电力系统存在和不存在随机增益变化时均方渐近稳定和镇定准则的时滞相关充分条件。
3)通过给出数值算例,对比文献[6]和文献[8]中的结果,证明了本文所提出的方法在最大允许时滞上限、最小H∞性能指标和电力系统弹性稳定上具备明显的优点。
本文的剩余部分安排如下。第一节建立了电力系统负荷频率控制的动态模型。第二节介绍了电力系统稳定性分析与控制器设计。第三节针对随机发生增益波动的电力系统设计了可靠负荷频率H∞控制器。在第四节,仿真结果验证了所提本文所提出方法的有效性,分别给出了时变时延最大允许上界、最小可靠的H∞稳定分析性能指标以及所设计的控制器增益的分析。结束语在第五节中给出。
符号定义:在本文中,上标“-1”表示矩阵逆,“T”表示矩阵转置,* 表示对称矩阵中的对称项。E{x}表示x的期望。Pr{α}表示事件α的发生概率。I表示适当维数的单位矩阵。n表示n维欧氏空间,n×m表示所有n×m矩阵的集合, diag{·}表示块对角矩阵。
1 电力系统负荷频率控制的动态模型
单区域电力系统的一般状态空间模型[34]可以描述为:
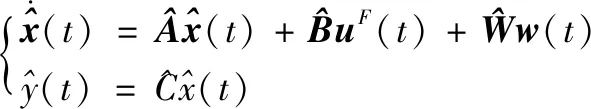
(1)
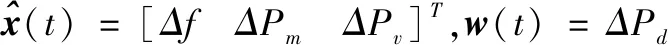
其具体参数的物理意义见表1所示。

uF(t)=α(t)u(t)
(2)
其中:u(t)为控制输入,α(t)为表征随机执行器故障现象的随机变量,假设满足Bernoulli分布,即:
Pr{α(t)=1}=ρ,Pr{α(t)=0}=1-ρ
(3)
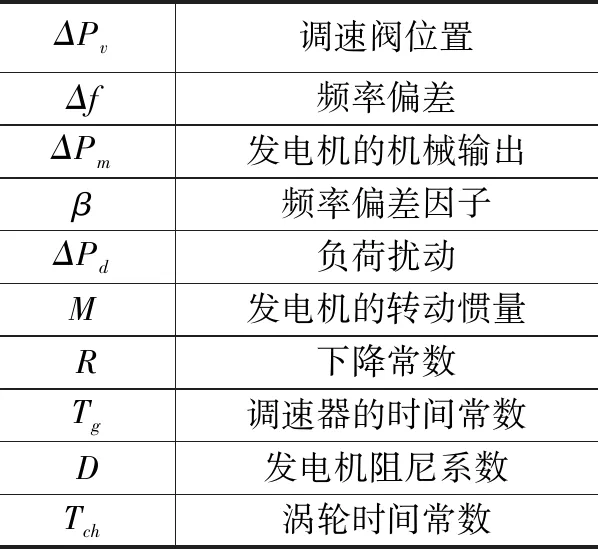
表1 电力系统参数
其中:ρ∈[0,1]是已知常数。由式子(3),我们得到E{ (α(t)-ρ) }=0和E{(α(t)-ρ)2}=ρ(1-ρ)。由于控制信号的传输,负荷频率控制的输入被认为是延迟ACE。然后,PI型负荷频率控制定义如下:
u(t)=-Ky(t-σ(t))
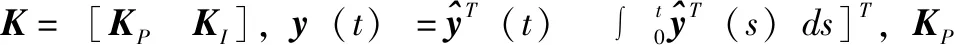


(4)
其中:
为了得到电力系统的时滞相关稳定性和镇定准则,首先给出如下引理。
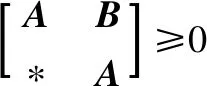
引理2[35]:对于任意正定对称矩阵Q∈n×n和u,v∈n,有:
±uTv≤uTQu+vTQ-1v
最后,给出本文的主要研究问题1。
问题1:给予系统(4)实现渐近稳定的条件,在以下目标下设计可靠的H∞负荷频率控制。
1)Lyapunov-Krasovskii函数是利用延迟ACE的全信息构造的。
2)建立了达到规定H∞性能指标的稳定准则,并给出了以下条件。
(1)w(t)=0条件下的电力系统是渐近稳定的。
(2)在零初始条件下,对于任意非零w(t)∈L2[ 0,∞)和给定的δ>0,有:
2 电力系统稳定性分析与控制器设计
在这一部分中,我们将推导出电力系统(4)稳定性分析的时滞相关充分条件和控制器设计的基本方案。

(5)
(6)
其中:
Θ=

Θ1,1=P1A+ATP1+P2+CTC+P3+P5,
Θ3=diag{-P3,-P4},
Π1=[A-ρBKC0W] 。
证明:考虑如下李雅普诺夫泛函:
其中:
V1(x(t))=xT(t)P1x(t)

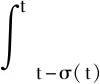
E{
(7)
E{V2(x(t))}=E{xT(t)P2x(t)-xT(t-h)P2x(t-h)+
(8)
E{
(1-τ)xT(t-σ(t))P5x(t-σ(t))}
(9)
积分项利用Jensen’s不等式,逆凸定理引理1可以很容易地得到如下不等式:
(10)
其中:η1=x(t)-x(t-σ(t)),η2=x(t-σ(t))-x(t(h)。将式(10)代入式(8),有:
E
yT(t)y(t)+δ2wT(t)w(t)}
(11)
其中:ζT(t)=[xT(t)xT(t-σ(t))xT(t(h)wT(t)]。从式(11),我们可以很容易地导出式(6)。如果式(6)成立,则有:
E{V(x(t))}≤E{-yT(t)y(t)+δ2wT(t)w(t)}
从0到∞两边积分即可得到:
E{V(x(∞))-V(x(0))}≤
对于任意非零w(t)∈L2[0,∞),这意味着
在零初始条件V(x(0))=0下。假设w(t)=0,存在一个标量φ>0使得:
E{
这说明系统(4)H∞性能指标下是均方渐近稳定的。因此,证明完毕。
基于线性矩阵不等式的时滞相关充分条件设计负荷频率控制方案的可靠H∞增益,给出定理如下。

(12)
(13)
(14)
其中:

Π2=[AR-ρBFC0W]。
此外,控制增益矩阵由K=FG-1设计。
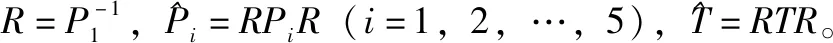
(15)
其中:
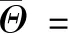

注释1:一般情况下,根据文献[6]和[7]的假设所知,他们都是基于一个增益矩阵的假设,对负荷频率控制的时滞相关稳定性条件进行了研究。假设增益矩阵未知,文献[6]和[7]中的方法将不在适用。而本文的方法能够设计未知控制增益K。
3 具有增益波动的弹性可靠负荷频率H∞控制器设计
在本节中,我们将设计具有随机增益波动和随机执行器故障的系统(4)的弹性可靠负荷频率H∞控制器。我们首先考虑弹性控制输入如下:
u(t)=(K+λ(t)ΔK(t))y(t-σ(t))
(16)
这里,K表示正常控制增益,ΔK(t)为加性增益扰动并满足ΔK(t)=LM(t)N,其中L和N为已知常数矩阵,未知矩阵M(t)满足MT(t)M(t)≤I。同时,随机变量λ(t)∈表示随机发生的控制器增益波动,其满足Bernoulli分布的白噪声,且Pr{λ(t)=1}=E{λ(t)}=γ,Pr{λ(t)=0}=1-γ,γ∈[0,1],E{(λ(t)-γ)2}=γ(1(γ)。同样,λ(t)和α(t)是不相关的随机变量。然后,电力系统(4)可以转换为如下形式:

(17)
由以上分析可知,满足均方渐近稳定性和H∞性能指标准则的理想弹性可靠H∞负荷频率控制可以归结为以下问题。
问题2:给定系统(17),为保证渐近稳定条件,在问题1条件下设计了弹性可靠H∞负荷频率控制器。

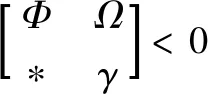
(18)
成立,
其中:
Φ=
Φ2,5=-ρCTFTBT,
Φ2,7=RCTNT,
Ω=
Ω5,5=γρBLQ4,
γ=diag{-Q2,-Q2,-Q3,-Q3,-Q4,-Q4,-I}。
再由K=FG-1得到弹性可靠控制器增益矩阵。

Cx(t-σ(t))-B(α(t)-ρ)γLM(t)×
NCx(t-σ(t))-ρB(K+(λ(t)-γ)LM(t)N)×
Cx(t-σ(t))-ργLM(t)NCx(t-σ(t))+
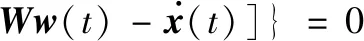
(19)
对于任意对称正定矩阵Qi(i=1,2,3,4),可得到:
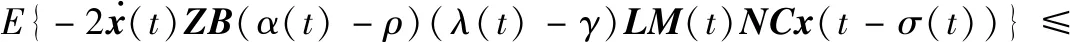
(20)

(21)

(22)

(23)
然后,计算弱无穷小生成元对V(x(t))随系统的演化的期望,可得:
E{ϑ(t)}



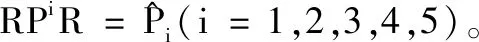
4 数值算例
下面通过文献[6]中的数值算例来论证本文所得结果的可行性和有效性。为了确立本文的主要研究目标,本文在以下几部分中分别计算了时变时延最大允许上界(MAUB)、最小可靠的H∞稳定分析性能指标以及验证本文所设计的控制器增益的有效性。
例:考虑了系统(4),其参数值列于表2所示。

表2 电力系统(4)参数值
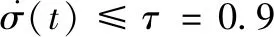

表3 文献[6]中对不同控制增益取值的σ(t)的最大允许上界

表4 定理1中控制增益的不同σ(t)取值的最大允许上界

表5 不同ρ下的σ(t)的最大允许上界的计算值
然后,我们给出H∞性能指标分析。取h=2,τ=0.5,增益KP=0.15,KI=0.1,基于定理1和文献[8],计算了最小H∞性能指标,并列于表6。由表6可知,本文所设计的控制方案在电力系统中有效地抵抗了负荷扰动。
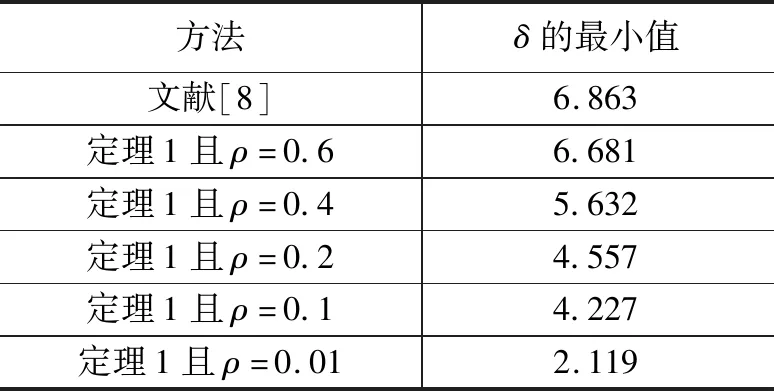
表6 δ的最小值计算
最后,我们分析本文所设计的控制器增益的有效性。设ρ=τ=0.1,h=0.2,ε=0.01和δ=8.5,根据定理2所得的控制增益矩阵为:
K=[1.221 1.223]
系统的频率偏差图如图1所示。从图1的仿真结果可以看出,系统在负载扰动和随机故障执行器存在的情况下是稳定的。

图1 频率偏差图
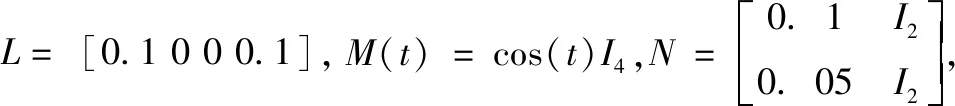
K=[3.544 0.733]
为了反映所开发控制设计方案的有效性,图2分别给出了弹性可靠控制增益下时变时滞σ(t)=4.9sin(t)+0.2的状态响应仿真结果。由图2可知,电力系统在本文所设计控制下,稳定性是能得到保证的。综上所述,即使在存在外部负荷扰动、随机执行器故障和随机增益变化的情况下,仿真结果证明了本文所提出的定理3的弹性可靠控制器能够很好地使电力系统稳定。

图2 σ(t)=4.9sin(t)+0.2下的频率偏差图
5 结束语
1)本文针对具有随机执行器故障、外部负载扰动和无随机增益变化的电力系统研究了其弹性可靠的负荷频率H∞控制问题。
2)通过构造合适的李雅普诺夫泛函,利用逆凸技术和线性矩阵不等式方法,得到了相应的稳定性定理和稳定性控制增益,保证了所提电力系统的均方渐近稳定性。最后通过数值模拟结果验证了本文所提出的方法的优越性和可行性。
3)所推导的条件得到的保守性小于已有结果。在我们的未来工作中,我们将把所提出的结果推广到具有时滞的多区域电力系统的输出反馈控制器的设计中。

