库岸边坡实时风险率预警模型及工程应用

徐江湖

（江西浔禹工程管理有限公司,江西 九江 332000）

1 引言

我国地域地质极为复杂,边坡灾害也较为常见,库岸边坡工程是重要的边坡修复工程,但由于复杂的力学行为以及外界环境变化,边坡中存在实时性动态变化的风险特性[1-3]。传统边坡预警方法难以实时性反应边坡的风险状态,不能灵敏掌握边坡风险状态[4,5],提出一种可实时性监测边坡风险状态的方法显得尤为重要。

已有诸多学者为改善传统方法的缺点进行了研究,杨妙帆[6]等利用不平衡推力理论对失稳边坡进行稳定性分析,预测了暴雨或地震条件下边坡的失稳特征。宋丹青[7]等采用GPS 对边坡位移进行监测,分析了稳定性影响因素,提出了边坡变形治理措施。张志会[8]利用神经网络学习,构建了非线性边坡变形预测模型,预测结果较好。

本文采用多测量点方法对边坡整体数据监测,并据此提出了边坡变形统计时空回归模型。根据概率基本原理,建立了风险率实时量化预测模型,并参考规范对安全级别不同的边坡风险临界值进行标定。建立质量控制图,通过实际工程对建立的实时边坡风险预警模型进行验证。

2 边坡风险监控模型

2.1 多点检测统计时空回归模型

传统边坡监控模型局限于单点测量,难以了解整体的边坡风险。根据实际工程的变形分析,对检测模型进行优化,采用多点测量坐标的数据,建立测量数据与预测函数之间的多坐标统计时空回归模型,旨在实时、动态的对边坡全局的风险进行统计。将测量点变形的水压、降水、温度以及时效分量作为边坡风险成因,建立的预警模型如下：

式中：XH为水压分量；XP为降水分量；XT为温度分量；为时效分量；H 为水位；P 为降水,=t/100。

设n 为空间位移场中每个测量点的样本数量,样本间的误差为εt相互独立,εt～N（0,S2）,k 为测量点数量。根据误差理论,上述模型中每个测量点的标准差可用下式表示：

式中：δit为测量点实测值；为拟合值。

2.2 安全指标的拟定

由于上式未对工程等级和质量做出规定,且标准差S 值不固定,该指标准确性存在较大问题。

3 边坡实时量化风险率模型

3.1 概率可靠度风险率模型

根据概率可靠度理论,在一般随机动态系统中,可通过概率密度函数将随机变量转化为随时间演化的偏微分方程。若边坡中某功能与n 个随机变量相关X1,X2,…Xn,则定义边坡功能函数Z=g（X1,X2,…Xn）,边坡稳定状态、边坡极限状态、边坡时效状态分别对应Z＞0、Z=0、Z＜0,设Z 的概率密度函数为 fz（Z）。定义Pf为边坡风险率,将功能函数与荷载和承载力联系起来,同时引入概率密度函数,则Pf可表示为：

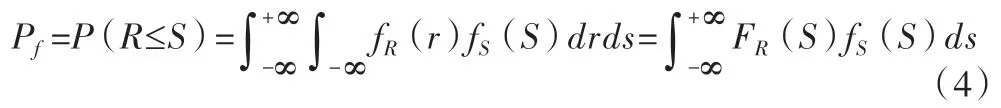
式中：S 为边坡荷载；R 为承载力；fRS（r,s）为R 与S 的联合概率密度函数；FRS（r,s）为联合概率分布函数；fR（r）与fS（S）为R 与S 的概率密度函数；Ωf为边坡失效域,即R,S。

综上所述，高中生作为社会的特殊群体，当前并没有树立良好的消费以及理财观念，极易出现盲目消费、过度理财等现象，对于学生接下来的发展来说是极为不利。在这种情况下，我们就应积极的采取一系列有效措施，通过端正理财心态，树立正确价值观，制定理财计划，培养良好理财习惯，结合课本知识，咨询父母意见，做好时间管理等有效手段，帮助高中生养成良好的消费以及理财观念，合理消费，合理理财。

式中：β为可靠度。

可靠度β与风险率Pf常用对照关系见表1。

表1 可靠度与风险率Pf 对照表

表1 可靠度与风险率Pf 对照表

3.2 建立实时量化风险率模型

根据可靠度理论所标定的风险率虽可对工程安全临界值进行联系,但由于其分析结果对材料的性能较为敏感,同时难以对边坡中实时发生的由材料性能变化而导致的风险率变化作出表征。为了改善上述缺点,现结合可靠度理论,构建实时风险率函数,可由实测值直接表征边坡实时风险率。

式中：Xi为测量点在时刻为i 时的实测值；为时i 刻模型拟合值；S 为时空回归模型标准差；φ（Xi）为Xi分布区间概率；F 为φ（Xi）、Pf的相关函数。

3.3 可靠度风险率与实时风险率结合

结合可靠度风险率Pf与实时风险率,依照两种风险率之间的关系,参考现有工程规范,对边坡运行的实时风险预警指标进行定量设计。分别从实测值Xi分布概率φ（Xi）、风险修正系数A、属性判断临界值β'对Pf和进行结合与转化。

（1）表2 表明了φ（Xi）与Pf之间的关系,示意图中,测量点分布概率φ（Xi）为斜线区域的灰色区域面积,边坡运行容许风险率Prf为红色区域面积。φ（Xi）与Prf间的关系随Xi的变化而变化,当边坡运行处于临界状态时,存在以下关系：

表2 边坡测量点运行状态判断关系式

表3 不同安全级别工程中极限状态的 与Pfr

表3 不同安全级别工程中极限状态的 与Pfr

（2）将测点序列﹛Xi﹜ 标准正态化,令形成服从的标准正态分布序列﹛Zi﹜,据此改写式（11）：

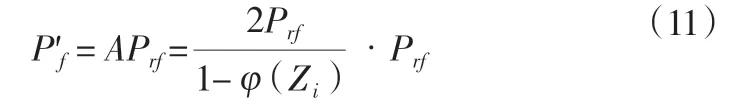
式中：φ（Zi）为正态化测量值的区间分布概率。

根据式（11）,测量值的风险判断见图2。将测量点的测量值映射在正态分布曲线上,可由判断临界值β'直观判断出该点风险状态。

图2 测量点风险判断

4 实时性边坡风险预警方法

4.1 风险状态等级标定

边坡风险状态可分为以下三个等级：安全状态,边坡运行安全稳定；预警状态,边坡运行处于危险临界值；应急状态：边坡运行及其不稳定,处于危险状态。一级与二级风险状态等级可由Pf1'和Pf2'界定,见图3。

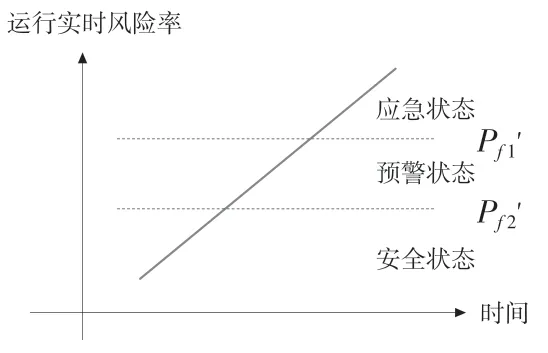
图3 边坡实时风险状态等级

4.2 预警方法

（1）训练区。根据2.1 节内容,假定某区域测点序列﹛Xi﹜,i=1,2,…,n,n 为时序长度,对该点建立统计时空回归模型,得出标准差S 与相关系数R。将测量点处R＞0.8 的测量点历史测量值与模型拟合值输入训练区,训练区见图4。

图4 实时性边坡动态预警示意图

（2）判断区。输入更新的测量值Xi+1以及对应库水位Hi+1、降水量Pi+1、温度Ti+1、时刻和测量点坐标x、y、z,得出模型预测值,将Xi+1与输入判断区,见图4。

（3）对照区。建立拟合值中心线XCL,根据预警指标中的两级风险等级,边坡风险预警指标可由一级控制线XUCL1、XLCL1与二级控制线XUCL2、XLCL2标定,如下所示：

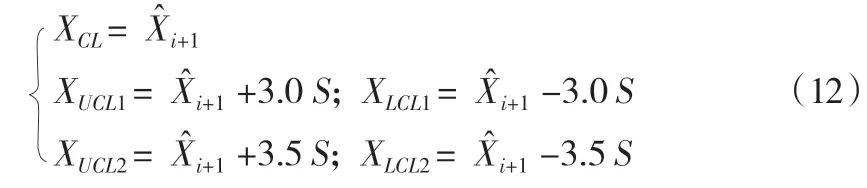
5 工程实例

某水电站的库岸边坡工程概况如下：边坡顺河方向长度为700 m,相对坡高为500 m～700 m。1400 m 高程以上的边坡坡度平均为25°～45°,1400 m 高程以下为22°～25°,存在较多级缓坡。坡面走向约S60°E,岩层产状近EW/S ∠30°～25°,结构为二元顺向坡。根据边坡1400 m 高程以下坡段的地质构造与破坏形式,将其分为区Ⅰ、Ⅱ、Ⅲ。

5.1 边坡变形统计时空回归模型

考虑边坡不同坡段的变形特点,对Ⅰ、Ⅱ、Ⅲ区分别建立变形回归模型,对边坡整体的变形特性作出统计。对边坡各区域地表设置23 个位移测量点,包含垂直和水平的测量位移数据。根据式（2）建立变形回归模型,将不同区域测量点的坐标（x、y、z）、降水量P、时刻、水位H、温度T 代入式（2）,分别建立各区域的变形统计时空回归模型。各区域单点的测量监控模型见表4～表6。每个区域的回归模型整体精度见表7。由表可知,所有模型的相关系数R 均大于0.8,说明模型准确性较高,可对边坡风险状态进行较为可靠的拟合预测。

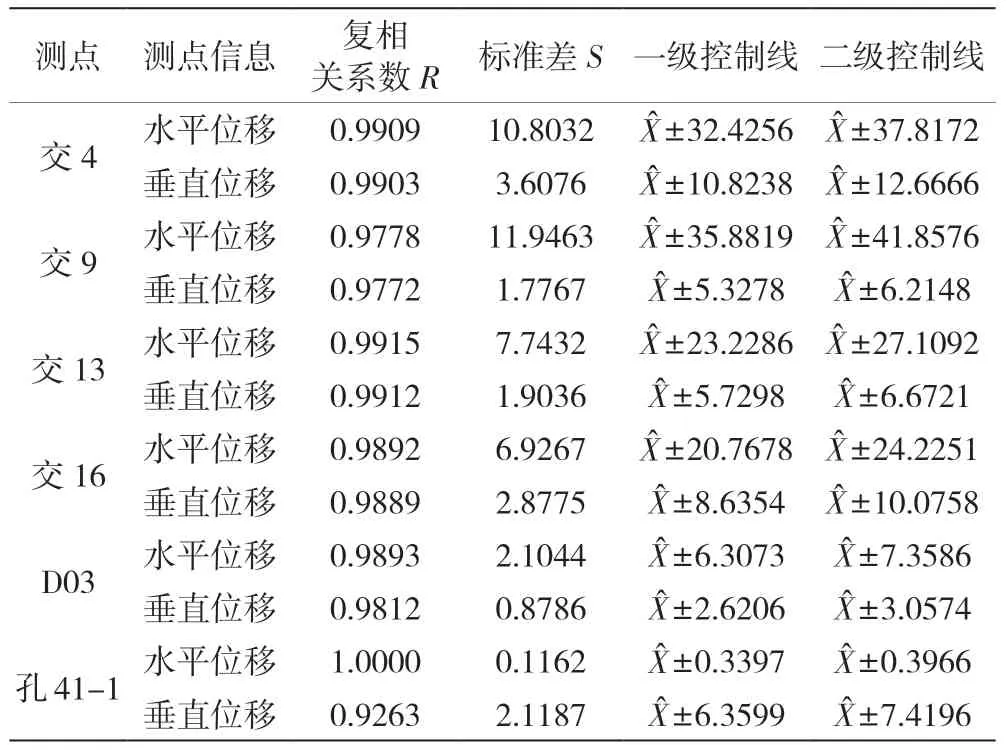
表4 Ⅰ区变形统计时空回归模型

表5 Ⅱ区变形统计时空回归模型

表6 Ⅲ区变形统计时空回归模型

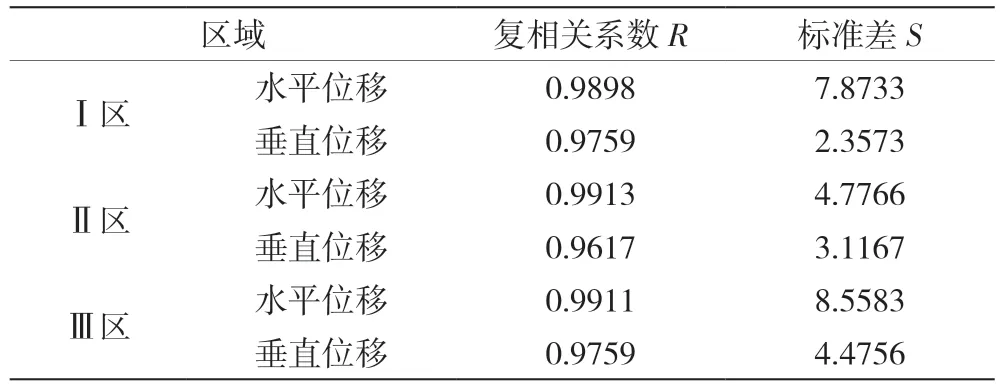
表7 各区域回归模型整体精度

5.2 边坡运行状态实时性动态预警

以区域Ⅰ为例,对边坡运行变形状态进行动态预警。根据上述的统计回归模型,将区域Ⅰ中精度较高的位移拟合值Xi的历史测量值和拟合值导入训练区。使用2019 年后的新测量点实测数据对模型的拟合值进行预测,并将预测值与实测值导入判断区。根据4.2 节所介绍方法建立中心线与监测安全控制线XCL、XUCL1、XLCL1、XUCL2与XLCL2。区域Ⅰ中各测量点历史测量值、拟合值、更新测量值、拟合值均在一级上下控制线内,表明区域Ⅰ中边坡运行处于安全稳定状态。

5.3 边坡实时性运行风险率分析

以交16 测量点为例,对该测量点进行边坡实时风险率模型分析,监测其风险率的实时变化。根据交16 历史监测数据,基于概率分布,将边坡风险率量化。结果表明,该测量点在2003 年6 月2 日边坡水平变形风险最大,分布概率为97.76%。令β=3.0,此时实时风险率为1.56×10-4；令β=3.5,实时风险率为4.64×10-6,风险率与对应两类预警级别指标1.35×10-3、2.33×10-4相比均较低。该测量点在2019 年9月4 日垂直变形风险率最大,测量值分布概率为97.77%,令β=3.0,此时实时风险率为1.65×10-4；令β=3.5,实时风险率为4.91×10-6,风险率同样低于对应两类预警级别指标。根据2019 年新测量数据对风险率进行计算,测量分布概率均处于30%～40%之间,实时风险率远低于预警指标,可判断该测量点位移状态较安全。

为了对实时风险率模型进行有效性验证,现假设2018 年12 月交16 测量点在水平方向出现了加速变形,取变形的初始速率为ν0=1.5mm/月,加速度为a=1.0 mm2/月,边坡风险率逐渐增大。如图5 所示,该测量点在2019 年8 月水平位移超过了质量控制图中的一级预警控制线,已处于预警状态；同年12 月,该测量点超过二级预警控制线,处于严重的边坡变形风险中,需立即对边坡工程进行排险、修复。对处于加速变形状态的交16 测量点进行风险率计算,结果与预警质量控制模型相同。

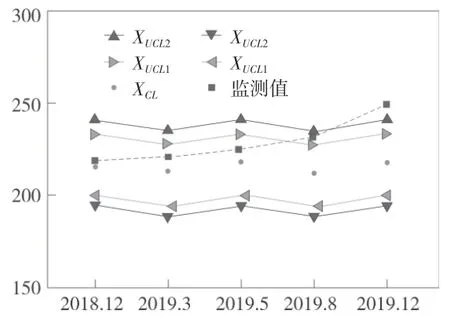
图5 边坡变形质量控制图

6 结论

（1）对边坡变形数据建立了多测量点时空统计回归模型,据此可对边坡整体变形状态做出判断,提高后续风险预警模型的准确性。

（2）根据概率理论,将边坡运行风险率正态化,建立风险率量化模型,设置不同安全级别下的边坡预警指标。

（3）以工程实例对风险率模型进行验证,结合质量控制图与实时风险率动态模型评价工程中边坡风险率,结果表明风险率模型具有高精度与可靠性。